顧及OSB改正的BDS-3新頻點精密單點定位精度分析

顧嘉琛 宋傳峰 田坤俊

1 山東無形信息技術有限公司，山東省泰安市御碑樓路67號，271000 2 武漢大學衛星導航定位技術研究中心，武漢市珞喻路129號，430079 3 山東理工大學建筑工程學院，山東省淄博市新村西路266號，255000

BDS-2/3采用雙頻偽距觀測量和雙頻載波相位觀測量進行偽距單點定位(SPP)和精密單點定位(PPP)，其理論方法和實現算法已經成熟[1-3]。然而，目前最常用的雙頻消電離層組合(IF)方法雖然可以消除一階項電離層誤差[4]，但在解算過程中會出現衛星端與接收機端間的硬件延遲，且地面接收機在接收信號時也會存在由天線和儀器設備等造成的測距碼偏差，上述偏差統稱為觀測量碼偏差[5-6]。觀測量碼偏差一直是精密定位研究中的熱點，通常將差分定位解算中的觀測量偏差稱為差分碼偏差DSB或DCB，將IF組合定位解算中的觀測量偏差稱為ISB[7-8]，國內外學者在觀測量碼偏差方面做了大量研究[9-14]。

近年來，隨著各系統支持頻點的不斷增多，DCB的估計與改正步驟也日趨繁瑣，有學者提出一種新的碼偏差估計方法OSB[5]。相較于DCB，OSB的估計、使用過程較為簡單，但其發展較晚、相關研究較少[6,15]。基于此，本文首先介紹OSB估計的理論方法；然后利用武漢大學(WHU)發布的OSB產品對BDS-2/3各衛星各頻點的OSB估計值進行穩定性分析；最后結合國際GNSS監測評估系統(iGMAS)實測數據，分析OSB改正對BDS-2/3的B1I/B3I舊頻點和B1C/B2a新頻點組合下SPP和PPP精度的影響。本文研究對于提升BDS-2/3精密定位服務性能具有重要意義。

1 OSB估計模型與穩定性分析

1.1 OSB估計模型

在估計各衛星各頻點的OSB前，首先需要估計衛星端與接收機端之間的DCB，然后對DCB估計值施加約束，計算出各衛星各頻點的OSB。在忽略多路徑誤差和觀測噪聲誤差的情況下，衛星與接收機之間的原始偽距觀測方程為：

(1)

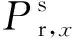
通過區分2頻點之間的偽距觀測量，可以得到無幾何組合觀測量GF：

(2)

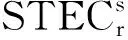
(3)

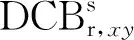
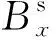
(4)

式中，Nx為1 a內觀測到的頻點x衛星總數。認為雙頻IF組合下衛星端2頻點的碼偏差IF組合以及接收機端2頻點的碼偏差IF組合均為0，則有：

(5)

通過式(5)的模型方法和約束條件，可以估計出各衛星各頻點1 a內的OSB值。

1.2 BDS-2/3衛星OSB穩定性分析

目前，中國科學院(CAS)、武漢大學(WHU)、歐洲定軌中心(CODE)及德國航空航天中心(DLR)等多家單位發布了OSB估計產品，但由于衛星剛組網成功且穩定運行不久，目前僅有CAS和WHU 2家單位的產品向外發布。本文利用WHU發布的2020-10-07(doy281/MJD59 129)～2022-02-06(doy037/MJD59 616)共計488 d的產品進行BDS-2/3各頻點OSB穩定性分析。

圖1為BDS-2/3衛星播發B1I、B3I、B1C和B2a頻點的OSB改正數時間序列，可以看出，各頻點的OSB改正值為-70～100 ns，各頻點的OSB估計數值較為穩定，無明顯波動。從數值上看，由OSB引起的等效距離誤差可達10 m量級，因此精密定位時必須將此誤差考慮在內。個別時段會出現明顯的跳變現象，原因可能是BDS衛星未參與當日OSB解算，導致估計觀測量偏差時采用了零均值基準約束。當參與解算的衛星數量發生改變時，約束條件也隨之變化，使得原先所有衛星的OSB日解值整體發生常數跳變。從圖1還可以看出，OSB值與衛星類型有關，BDS-2衛星B1I和B3I頻點的OSB估計值偏低，BDS-3衛星B1C和B2a頻點的OSB值各不相同。

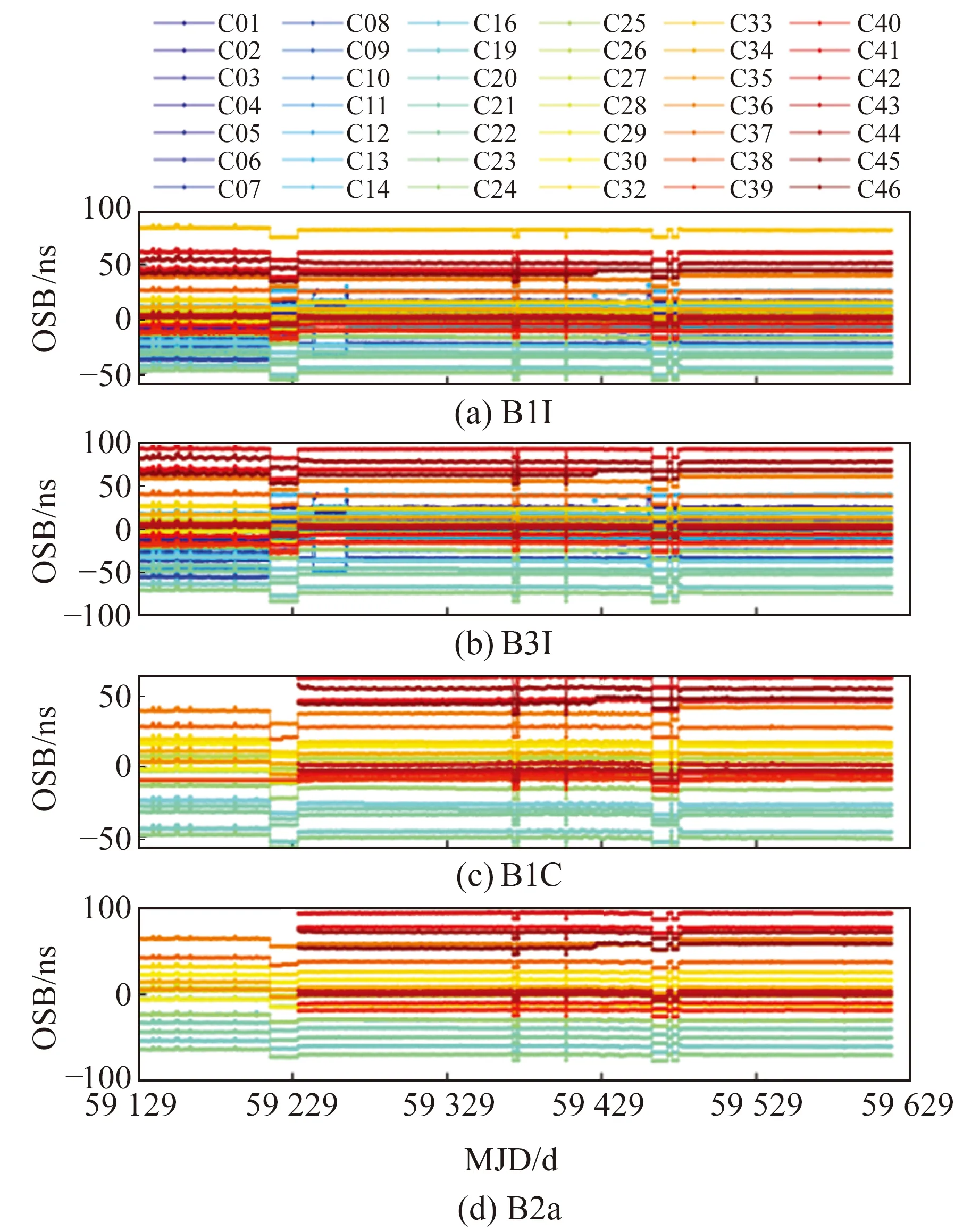
圖1 各頻點OSB值時間序列Fig.1 Time series of OSB values at each frequency

圖2為BDS-2/3各衛星各頻點的均值和STD值，可以看出，BDS-2衛星播發的B1I和B3I頻點的OSB均值相差不大，整體穩定在-50～50 ns之間；而BDS-3衛星播發的B1I、B3I、B1C和B2a頻點的大部分OSB均值都穩定在某個常數值內，只有個別OSB估計均值存在差異，如C33衛星，這也說明OSB估計值與衛星和接收機的硬件設備有關。從各衛星OSB估計STD值可以明顯看出，BDS-2衛星B1I和B3I頻點OSB估計值STD精度較低，說明OSB穩定性較差，但各衛星的精度較為穩定，沒有較大跳變。其中，BDS-2衛星B1I頻點OSB估計STD值約為6 ns，B3I頻點OSB估計STD值約為9 ns。對于BDS-3衛星4個頻點而言，B1I、B1C和B2a頻點OSB估計STD精度較高，均穩定在3 ns以內；而BDS-3部分衛星B3I頻點的OSB估計值穩定性較差。綜上所述，WHU發布的BDS-2/3衛星B1I、B3I、B1C和B2a各頻點的OSB估計值STD精度分別為3.41 ns、5.87 ns、2.04 ns和2.32 ns，其中新頻點B1C和B2a的OSB穩定性較好。

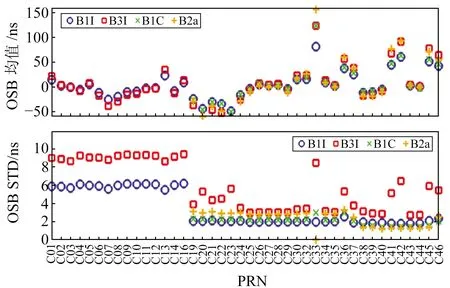
圖2 BDS-2/3各衛星各頻點OSB均值和STD值Fig.2 OSB mean value and STD value of each satellite at each frequency point of BDS-2/3

2 OSB改正算例分析

為評估OSB改正對BDS-2/3衛星新舊頻點SPP及PPP精度和收斂時間的影響，本文選擇8個能夠接收到BDS-2/3衛星所有頻點的iGMAS測站(BJF1、CHU1、GUA1、KUN1、LHA1、SHA1、WUH1及XIA1)實測數據。為避免偶然性，時間跨度選為2022-01-01～31共31 d，BDS-2/3的廣播星歷和精密星歷由武漢大學IGS分析中心提供。首先利用自行編寫的軟件對各個測站的觀測數據進行OSB改正；然后利用日本東京海洋大學T.TAKASU開源發布的RTKLIB軟件對OSB改正前后的BDS-2/3數據進行SPP和PPP解算；最后將iGMAS官方發布的測站坐標作為真值，分析OSB改正前后對解算結果的影響。具體解算策略見表1。

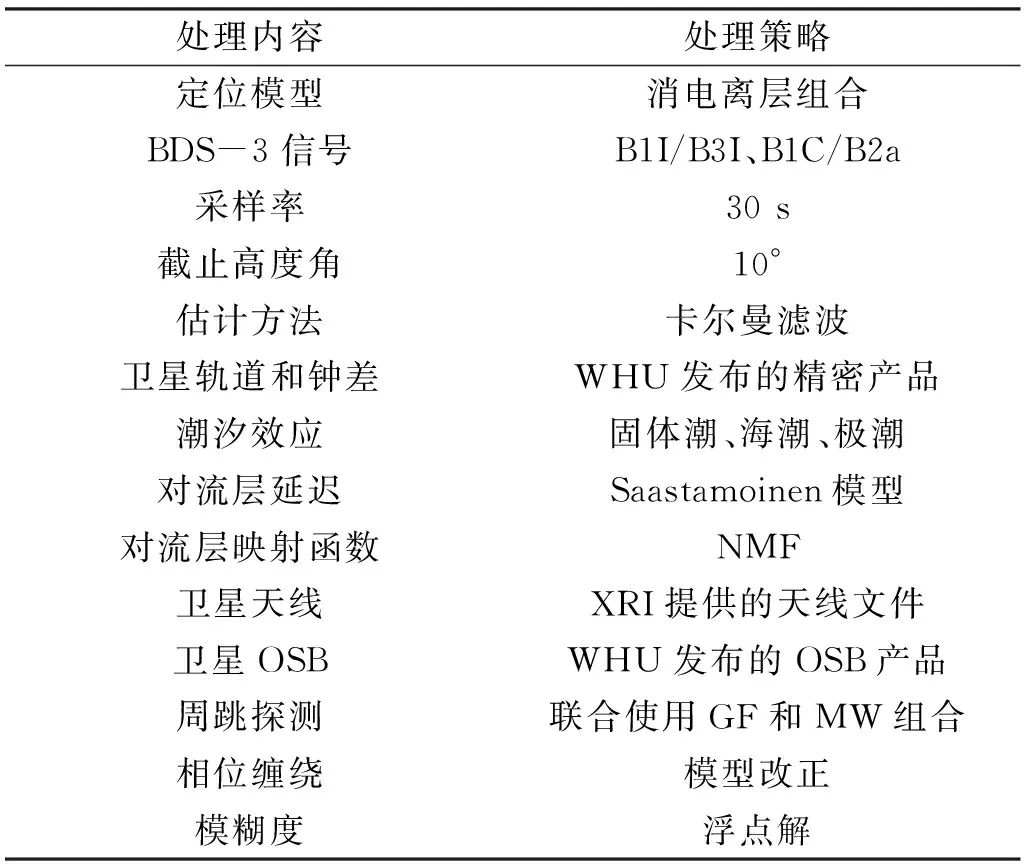
表1 精密定位處理策略

首先統計能夠觀測到的B1I/B3I和B1C/B2a頻點的可見衛星數量，圖3為2022-01-07～13 iGMAS拉薩跟蹤站(LHA1)所觀測到的各頻點衛星數量。目前BDS衛星已建網完成，地面接收機可以穩定接收到約12個B1I/B3I頻點的BDS-2/3衛星及8個B1C/B2a頻點的BDS-3衛星，均滿足SPP和PPP的定位需求。

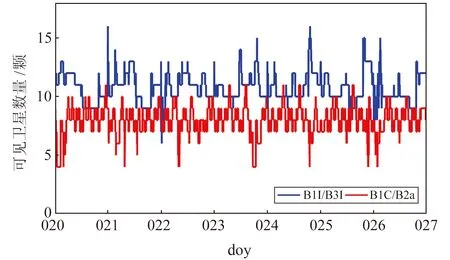
圖3 可見衛星數量Fig.3 Number of visible satellite

2.1 SPP精度分析

計算OSB改正前后8個iGMAS測站31 d內B1I/B3I組合和B1C/B2a組合的SPP，各測站在3D方向上的RMSE精度統計見圖4。可以看出，OSB改正對SPP解算精度的提升并不明顯，可能是因為BDS衛星的星歷精度較差，SPP解算中OSB改正所提升的精度被星歷引起的誤差所吸收。從雙頻組合的SPP精度對比可以看出，改正后B1I/B3I組合的SPP精度可達2.53 m，而B1C/B2a組合的SPP精度僅為3.84 m。二者精度相差較大，原因可能是B1I/B3I的觀測衛星數量相對較多，衛星空間分布的幾何結構較好，在解算時坐標參數的計算精度更高。通過對比可以看出，部分測站的解算精度較低，這可能與測站環境和測站接收信號的觀測質量有關。

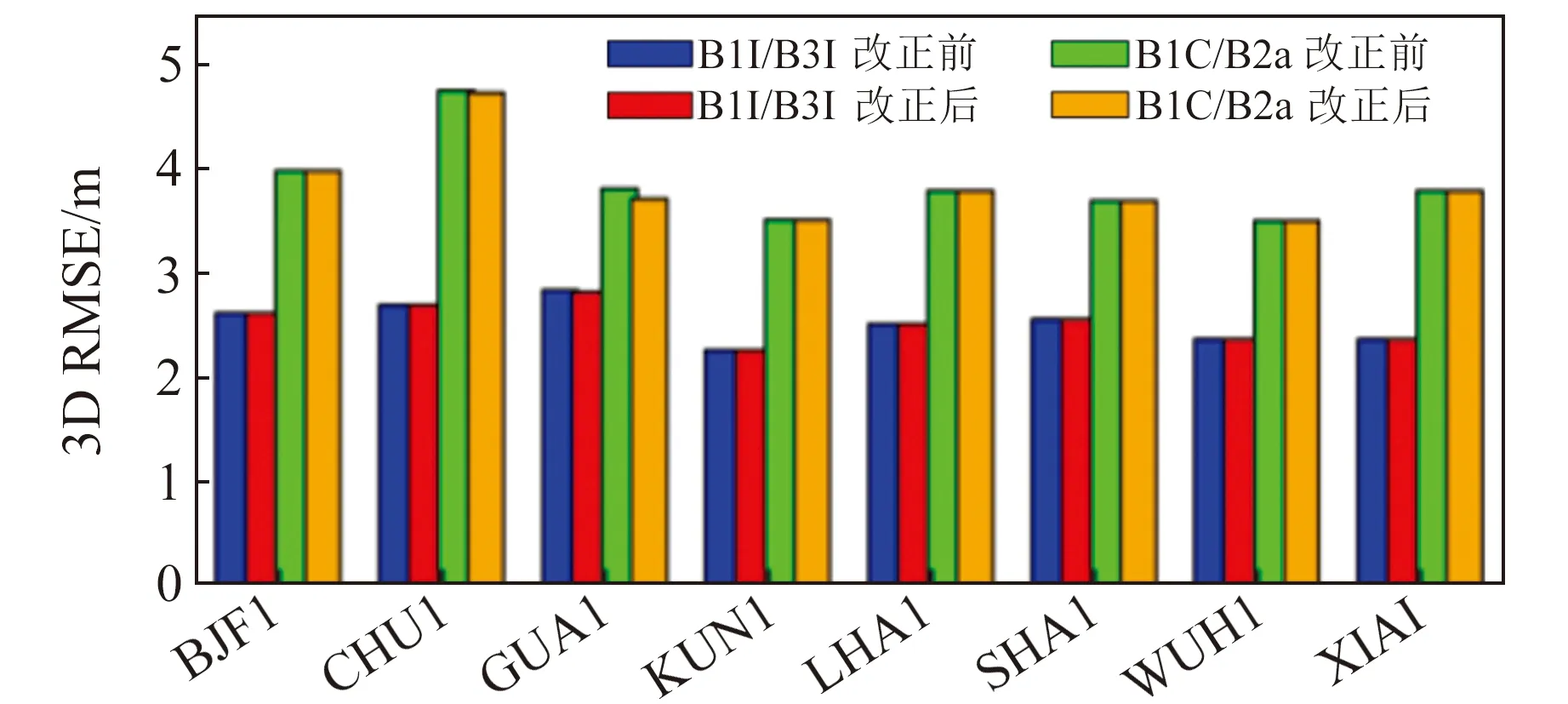
圖4 OSB改正前后SPP精度Fig.4 SPP accuracy before and after OSB correction

2.2 PPP精度分析

在PPP解算方面，OSB改正前后8個iGMAS測站31 d內B1I/B3I組合和B1C/B2a組合的收斂時間和3D方向上的RMSE精度統計見圖5。由圖5(a)可知，OSB改正對BDS-2/3衛星B1I/B3I舊頻點組合的PPP精度影響較為明顯，改正前各測站PPP定位精度在3D方向上的RMSE約為9.7 cm，收斂時間約為41 min；改正后各測站PPP定位精度在3D方向上的RMSE約為7.7 cm，提升約20.6%，收斂時間約為38 min，提升約7.3%。由于B1I/B3I解算時利用的BDS-2地球同步軌道(GEO)衛星的軌道精度較低，因此會影響PPP精度、收斂時間及OSB改正效果。

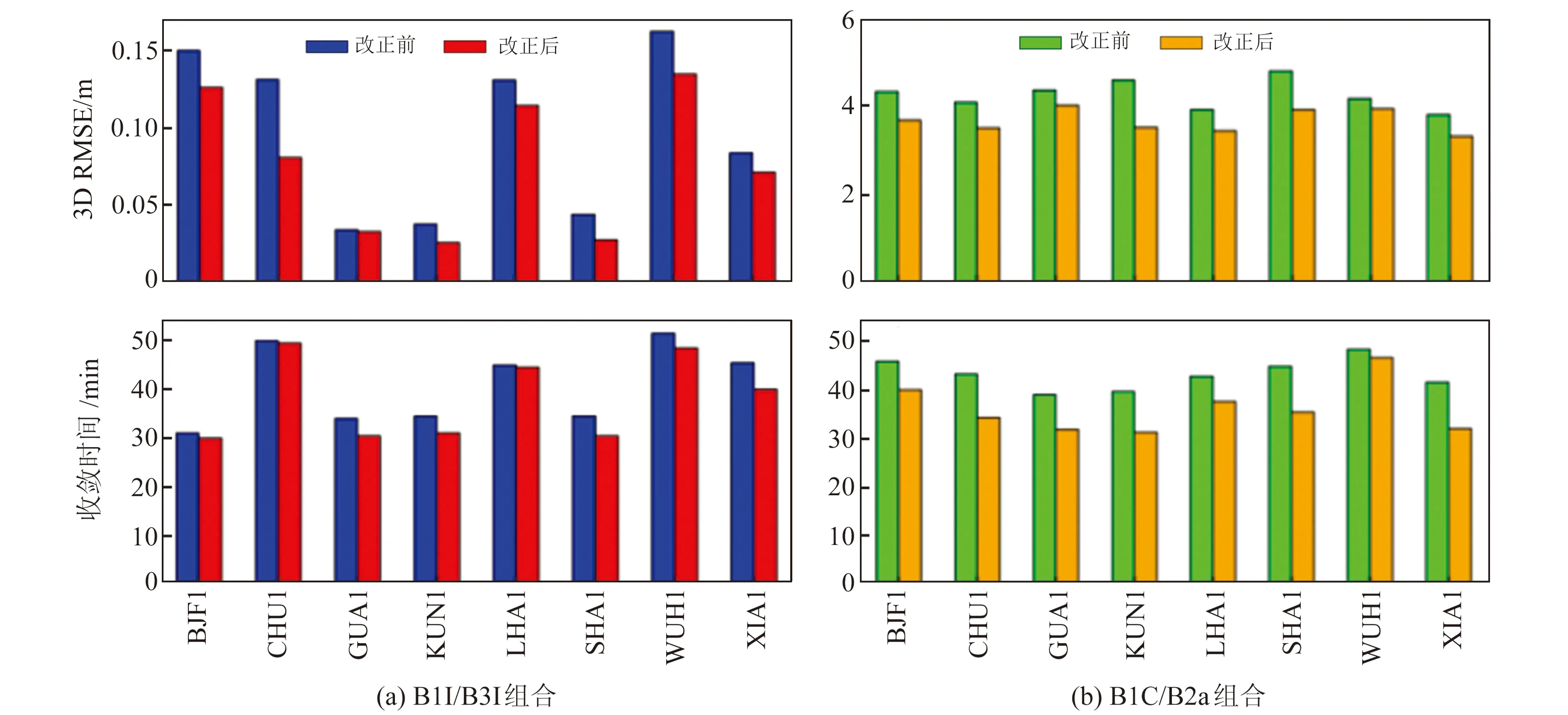
圖5 各測站OSB改正前后PPP精度和收斂時間Fig.5 PPP accuracy and convergence time before and after OSB correction at each station

由圖5(b)可見，OSB改正前B1C/B2a新頻點組合各測站PPP精度約為4.2 cm，收斂時間約為43 min；OSB改正后定位精度約為3.7 cm，提升約11.9%，收斂時間約為36 min，提升約16.3%。由于BDS-3衛星均為中軌道(MEO)衛星，相比于GEO衛星具有更好的軌道精度，且運行更加穩定，因此雖然整體上接收B1C/B2a頻點的衛星數量少于B1I/B3I，但B1C/B2a的PPP結果更優且更加穩定。從SPP和PPP的解算結果來看，OSB改正對PPP定位性能的影響較大，因此在利用BDS-2/3數據進行PPP解算時需進行OSB改正。

3 結 語

1)BDS-2/3衛星B1I、B3I、B1C和B2a各頻點的OSB估計均值為-80～70 ns，STD精度分別為3.41 ns、5.87 ns、2.04 ns和2.32 ns，BDS不同類型衛星在不同頻點上的OSB值也各不相同。綜合來看，B1C和B2a頻點的穩定性較好。

2)在SPP方面，OSB改正對B1I/B3I組合和B1C/B2a組合的定位精度影響并不明顯。OSB改正后，B1I/B3I組合和B1C/B2a組合的SPP精度分別為2.53 m和3.84 m。

3)在PPP方面，OSB改正對B1I/B3I組合和B1C/B2a組合的定位精度影響較為明顯。對于B1I/B3I組合而言，PPP精度和收斂時間分別提升20.6%和7.3%；B1C/B2a組合的PPP精度和收斂時間分別提升11.9%和16.3%。

本文僅分析BDS-2/3衛星4個頻點的OSB改正情況，隨著能夠接收BDS信號的測站數量不斷增多，OSB估計精度也隨之提高。此外，隨著地面測站的增多，BDS-2/3衛星的精密軌道精度不斷提高，SPP和PPP精度也會得到進一步提升。為增加數據觀測量，需采用多系統PPP模式進行GNSS定位，后續將進一步研究GNSS多系統OSB改正對動態PPP精度的影響及實時OSB產品的生成。

致謝:感謝武漢大學IGS分析中心和iGMAS分析中心提供的幫助和數據支持。