基于自適應粒子群算法的軌下基礎病害識別*

伍偉嘉 楊 儉 袁天辰 邵志慧

(上海工程技術大學城市軌道交通學院，201620，上海∥第一作者，助理工程師)

軌下基礎結構作為軌道系統重要的承載結構，其作用是將高速列車運行所產生的沖擊載荷傳遞給路基并實現減振效果。隨著我國鐵路列車運行速度的增加和承載能力的增大，軌下基礎必然會承受更大的沖擊載荷，而軌下基礎病害將會隨著軌道系統運營時間的推移逐漸顯現，進而威脅行車安全。因此，實現對軌下基礎病害快速且高效的診斷和識別是保障列車安全運行的關鍵。

軌下基礎病害識別的首要問題是如何獲取軌下基礎結構處于病害狀態時的故障特征。近年來，小波分析因具有多尺度特性而被國內外學者廣泛應用于機械結構和大型土木結構故障診斷領域，特別是故障特征提取方面。文獻[1]利用小波變換和奇異值分解提取了水電機組振動的故障特征，并采用概率神經網絡算法對所提取到的特征向量進行分類，具有較高的分類準確率。文獻[2]基于集成經驗模態分解和可調Q-因子小波變換實現了對滾動軸承早期故障的特征提取。由于小波變換沒有對振動信號的高中頻部分進行分解，導致提取到的特征可能無法完全反映軌下基礎結構病害的故障特征信息。為了避免由于小波分解本身分析頻段所帶來的問題，文獻[3]將小波包分解運用到了滾動軸承的故障診斷中，并成功判斷出了滾動軸承的故障類型。

在提取故障特征信息后需要對故障模式進行識別，相較于神經網絡算法，SVM(支持向量機)算法在處理高緯度、小樣本和非線性數據方面有較大的優勢，且其還具有很強的自學能力和泛化能力。但SVM算法中對于參數的選擇極大地影響了故障識別分類的準確率，因此國內外學者采用智能算法優化SVM參數，如GA(遺傳)算法、蟻群算法和網格搜索算法等。但上述這些優化算法存在一些不足之處：GA算法參數較多且尋優速度慢；蟻群算法計算量大且不適用于復雜問題；網格搜索算法運算時間會隨著搜索步長的減小而陡增。粒子群算法不僅收斂速度較快，且在解決復雜的非線性問題上有較好的表現。針對軌下基礎病害識別，本文利用小波包分解對軌下基礎病害振動信號進行三層分解，并提取分解后的底層能量作為后續故障分類的輸入，利用自適應粒子群算法聯合SVM算法對病害進行識別，以較好地識別出不同的軌下基礎病害。本文研究可為軌枕的故障診斷以及預測提供理論及參考依據。

1 車輛-軌道耦合動力學模型與病害模擬

1.1 車輛-軌道耦合動力學模型

采用如圖1所示的車輛-軌道垂向耦合動力學模型，其中車輛系統是由車體質量mc、轉向架質量mT、輪對質量mw組成的一個多剛體系統，并以速度v在軌道模型上運動，考慮車體和前后轉向架的沉浮運動自由度(zc,zT1,zT2)與點頭運動自由度(βc,βT1,βT2)，以及4個輪對的垂向運動自由度(zWo,o=1,2,3,4)，則車輛系統的運動方程為：

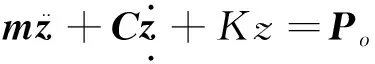
(1)

式中：

m、C、K——分別為車輛系統的質量、阻尼和剛度矩陣；

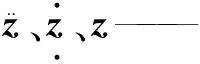
Po——系統力向量。

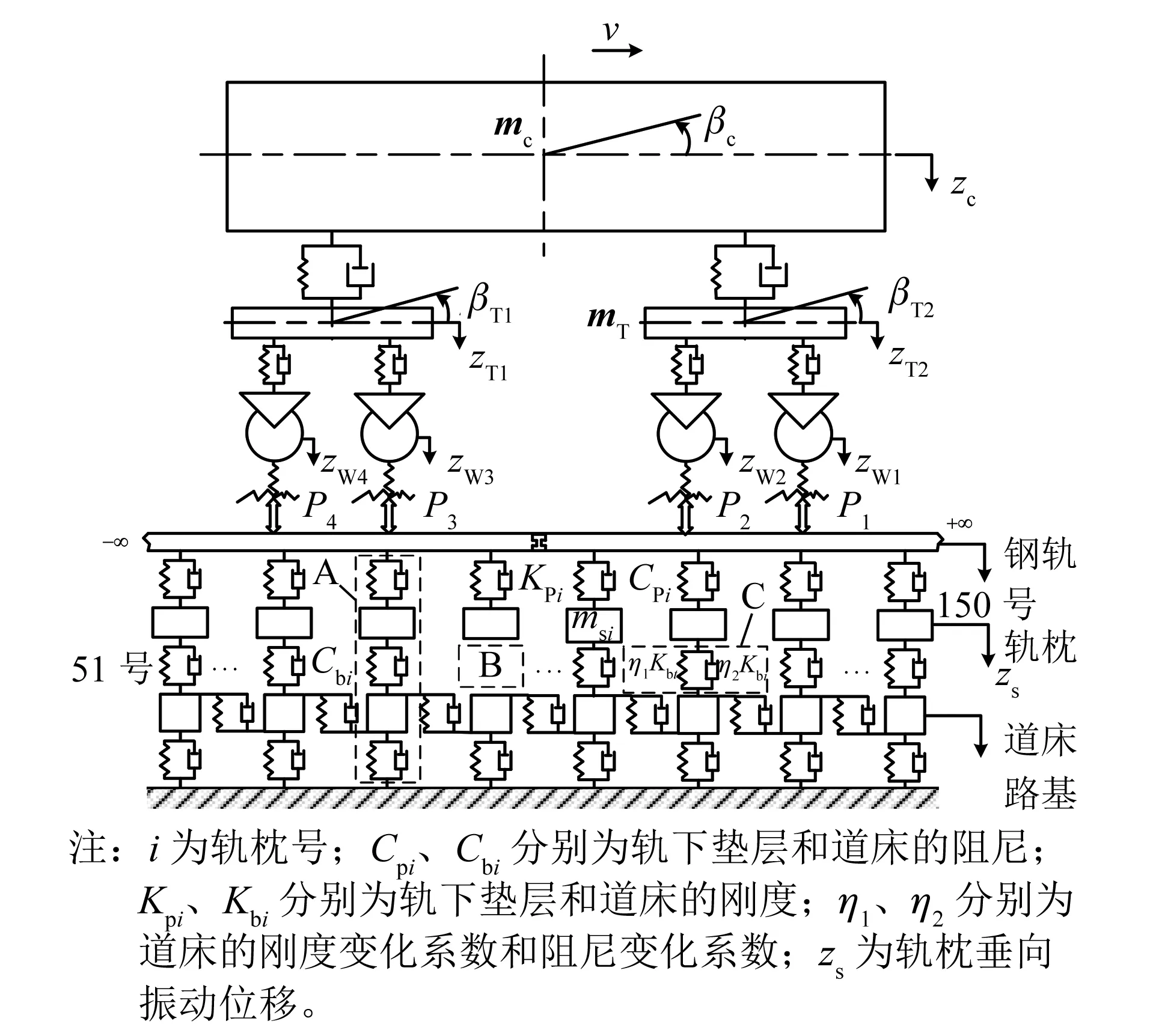
圖1 車輛-軌道耦合動力學模型(含病害)Fig.1 Vehicle-track coupling dynamics model (including diseases)

軌道系統由鋼軌、軌下基礎(包括軌枕和道床)以及路基組成，其中鋼軌可以視為連續彈性離散點支撐上的無限長Euler梁，軌下基礎可模擬為雙質量、三層彈簧-阻尼振動模型(見圖1中的模型A)，并按軌枕間距沿縱向離散。本文不涉及鋼軌、道床和路基的振動方程，具體可參考文獻[4]。文獻[5-6]的研究表明：通過改變模型中的Cbi和Kbi可以模擬軌下基礎病害，例如：軌枕完全空吊工況(見圖1中的模型B)即完全失去工作能力，可設Kbi=Cbi=0；對于道床板結或松散工況(見圖1中的模型C)，則設Kbi,ne=η1Kbi，Cbi,ne=η2Cbi，對于不同程度的病害，η1、η2的取值范圍為[0.1,10.0]。

1.2 軌下基礎病害仿真

采用Matlab軟件建立車軌耦合模型，時間步長設置為1×10-4s，取軌道長度L=120 m，軌枕間距Ls=0.6 m，選取位于軌道系統中心位置的51號—150號共100個軌枕截面單元，以100號軌枕為振動響應分析對象。不同工況下的軌下基礎模擬參數如表1所示。根據表1的仿真工況，以列車行駛速度為200 km/h為例，軌枕在不同工況下的振動加速度時域譜和功率譜仿真結果如圖2所示。

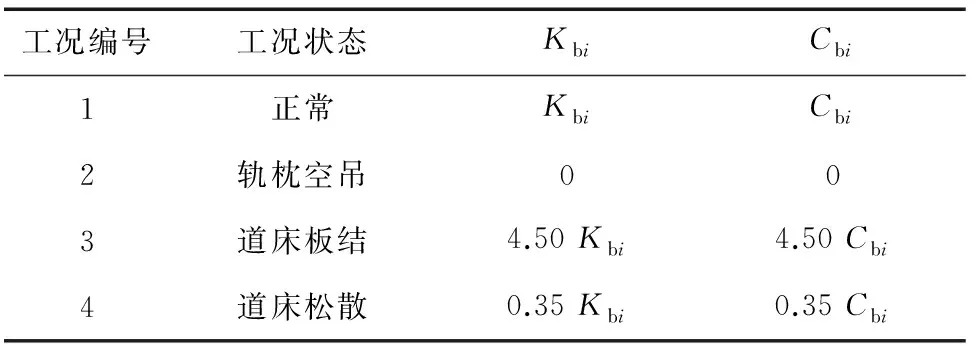
表1 不同工況下的軌下基礎模擬參數

由圖2 a)和圖2 b)可知，軌枕空吊工況下的軌枕振動加速度的幅值比正常工況下要大很多，而從功率譜方面來看,其在100～102Hz頻率范圍內有明顯的變化；從圖2 c)—圖2 f)中可以看出，道床板結和道床松散工況下的軌枕振動加速度較正常工況變化不是特別明顯，而從功率譜方面來看，其在頻率低頻區變化不明顯，在頻率高頻區變化稍有區別。故需要對軌枕振動加速度進行特征提取，且要求特征提取方法既可以反映軌枕振動加速度在時域上的變化，又可以體現軌枕振動加速度在頻域高頻和低頻區域的特征。

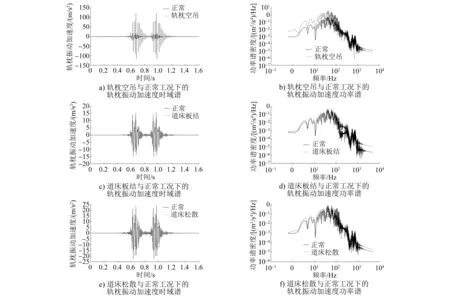
圖2 列車速度為200 km/h時軌枕在不同工況下的振動加速度時域譜和功率譜仿真結果

2 基于SVM的病害特征識別

2.1 基于粒子群算法的SVM參數優化

SVM算法是一種用于解決凸二次優化問題的機器學習算法，其核心內容是找到一個分類超平面并將其作為決策曲面，進而最大化正反例之間的隔離邊緣。相較于其他人工智能算法，SVM算法在解決高維度、小樣本，以及非線性模式識別方面有很大的優勢。PSO(粒子群優化)算法是一種根據鳥類捕食行為所提出的群體智能算法，與GA算法相比，PSO的SVM參數尋優方法不需要進行選擇、交叉、變異等復雜操作，具有收斂速度快、尋優精度高等特點。因此本文利用PSO算法對SVM進行參數尋優。

PSO算法的基本原理為：在n維空間中隨機地產生一些粒子，每個粒子代表了所求優化問題的一個潛在最優解，每個粒子的特征信息用位置x、速度v及適應度三項指標描述，其中適應度指標由目標函數確定，用于反映某個粒子與其他粒子之間的優劣程度；每個粒子按照特定的方程以不同的速度和位置進行移動，在移動過程中每個粒子都會計算該位置的適應度值，從而得到該粒子的局部最佳位置；通過粒子之間的交互協作和信息共享，可以獲得整個粒子群體的最優適應度值和最佳位置，每個粒子在移動過程中也會根據個體和整個群體的最佳位置及適應度，動態地調整、更新位置和速度，通過逐步迭代最終實現最優解的尋找。

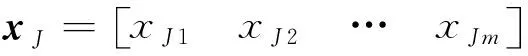
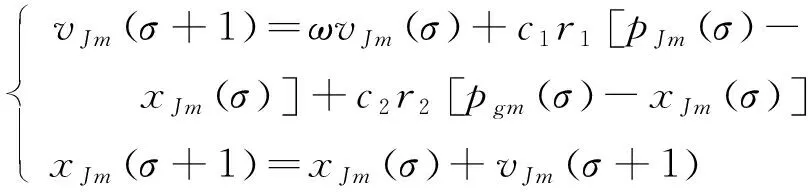
(2)

式中：

pgm——m維下的種群全局極值；

σ——種群進化代數；

ω——慣性因子，通常取為0.8；

c1、c2——加速因子，取值范圍為[0,2]；

r1、r2——分別為兩個相互獨立的隨機數，取值范圍為[0,1]。

基于PSO算法對SVM進行參數尋優的算法流程如圖3所示。

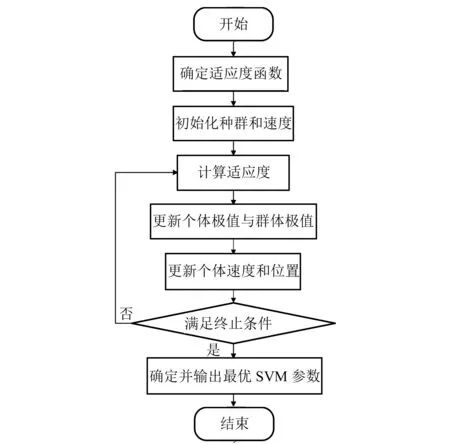
圖3 基于PSO算法優化SVM參數的算法流程圖

2.2 自適應粒子群算法參數優化

為了進一步加快PSO算法的收斂速度，采用一種自適應變化參數為c1、c2、ω的PSO算法，即APSO (自適應粒子群) 算法。APSO算法主要利用進化狀態評估(ESE)將種群的進化細化為搜索、發現、收斂和跳出等4個階段，結合自適應變化參數對PSO算法進行改進。

在PSO算法中，ω的取值會影響粒子的搜索能力，其值越大，局部搜索能力越弱；其值越小，全局搜索能力越弱。由此可知，在搜索階段時需要ω的取值較大，而在發現階段時需要ω的取值較小，故ω的取值需要隨著進化狀態的改變而改變，可以表示為：

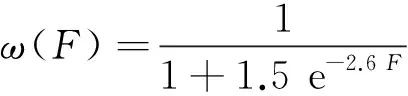
(3)

式中：

F——進化因子，?F∈[0,1]。

c1、c2是調整粒子朝著局部和全局最佳位置運動的步長變量，因此其也需要隨著進化狀態的改變而改變。在搜索階段時，需要搜索到盡可能多的個體最優值，即較好的局部搜索能力，此時需要增大c1并減小c2，以避免算法陷入局部最優；在發現階段時，粒子利用周圍的局部信息使種群向局部最優位置移動，此時需要小幅增大c1并小幅減小c2，以避免過早收斂；在收斂階段時，種群已經抵達全局最優位置附近，此時需要同時增大c1和c2，以引導其他粒子向其聚集；在跳出階段時，當前區域的局部最優粒子跳出并遠離所在的聚類，快速向新的較優區域移動，同時該聚類中的其他粒子也會跟隨該局部最優粒子快速移動，此時需要減小c1并增大c2。

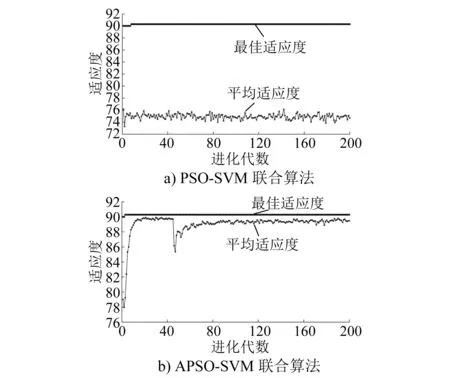
圖4 適應度曲線Fig.4 Fitness curve

2.3 基于APSO-SVM算法的軌下基礎病害識別

本文基于APSO-SVM聯合算法對軌下基礎病害進行識別。將由1.2節仿真獲得的不同工況條件下的軌枕振動加速度數據分成訓練集和測試集，其中：前90組數據作為訓練集；后10組數據作為測試集。首先對二者進行三層小波包分解并計算最后一層的能量，然后將所得到的特征向量集合進行歸一化處理，最后將不同工況的特征向量集合輸入SVM算法。為了驗證APSO-SVM聯合算法的有效性，采用PSO算法優化SVM參數，將其作為對照組。利用APSO-SVM聯合算法和PSO-SVM聯合算法進行軌下基礎病害識別，其適應度曲線和分類識別結果分別如圖4和圖5所示。同時，為了驗證APSO-SVM聯合算法的魯棒性，在車速為100～140 km/h條件下，利用APSO-SVM算法獲得的病害識別準確率結果如表2所示。

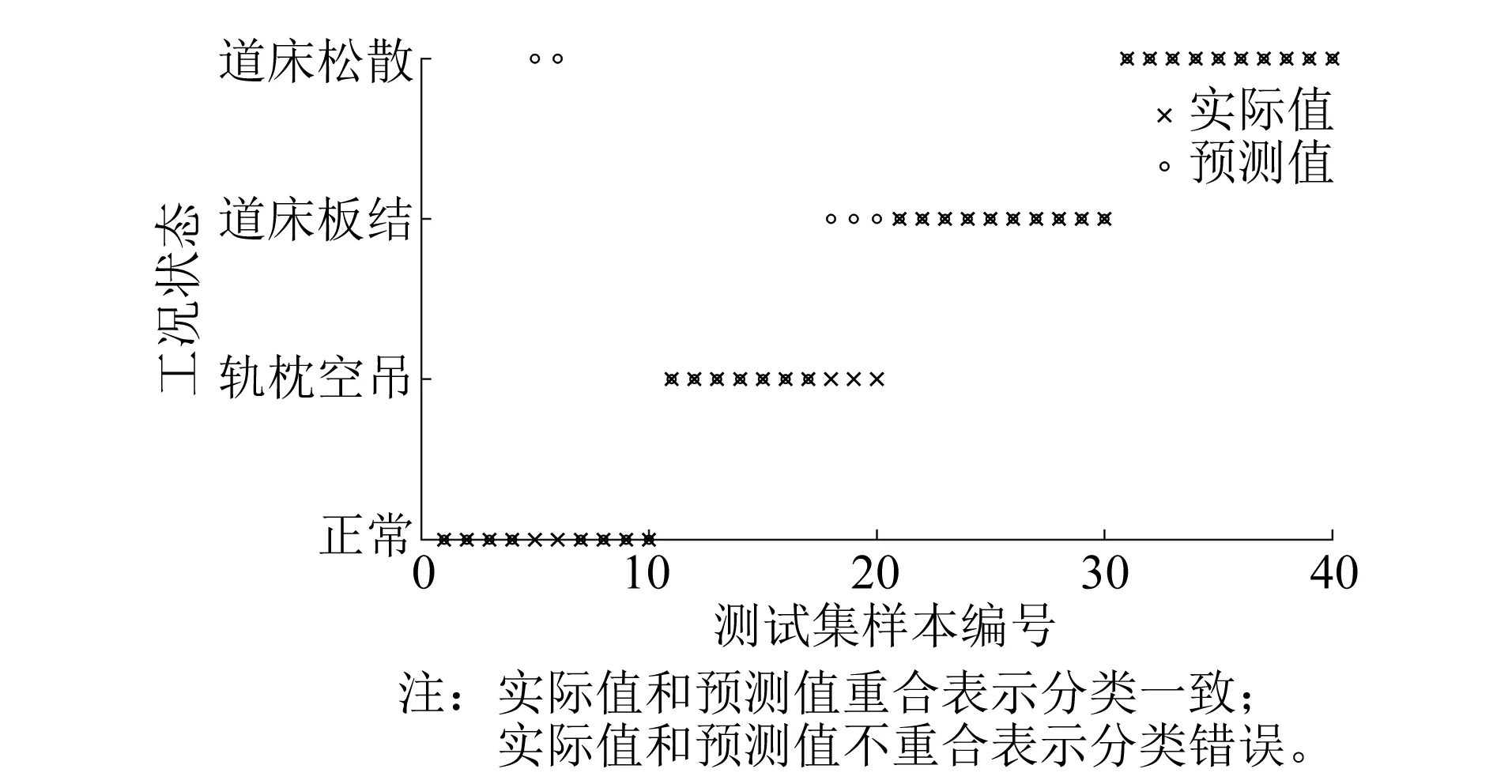
圖5 APSO-SVM分類識別結果Fig.5 APSO-SVM classification and recognition results

表2 不同車速條件下的病害識別準確率結果

由圖4可知，PSO-SVM聯合算法的種群在第10～15代之間就收斂了，而利用APSO-SVM聯合算法的種群在第5代左右就已經收斂，并且前者的運算時間為1 464.8 s，后者的運算時間為1 046.92 s，說明利用APSO-SVM聯合算法減少了收斂時間。由圖5可知，測試樣本數量為40個，有35個測試樣本的預測值與實際值重合，分類準確率為87.5%(35/40)，說明APSO-SVM聯合算法可以較準確地對軌下基礎病害進行識別。由表2可知，不同速度條件下，APSO-SVM算法的識別準確率均大于等于80.0%，具有一定的魯棒性。

3 結語

本文基于時頻域分析方法提取了軌下基礎不同工況的振動加速度特征，采用SVM算法對軌下基礎病害進行了分類，并利用APSO-SVM聯合算法優化SVM參數。主要獲得以下兩個結論：

1) 基于車輛-軌道耦合動力學模型對軌下基礎病害進行了仿真研究，并對比了不同病害條件與正常工況條件下，軌枕振動加速度的時域譜和功率譜變化情況。研究結果表明：在軌枕空吊工況下，軌枕振動加速度的時域幅值出現了較大的變化；在道床板結和道床松散工況條件下，其變化不明顯；不同病害工況下，軌枕振動加速度在高頻和低頻區域的功率譜有著不同程度的變化。

2) 為了進一步提高PSO算法在優化SVM參數選優時的收斂速度，提出一種自適應粒子群算法。識別結果表明：在保證識別準確率的前提下，所提算法可以有效提高收斂速度；對不同車速條件下的軌下基礎病害進行識別，識別準確率≥80.0%，說明所提算法具有較好的魯棒性。