基于威布爾分布及海因里希法則的動車組車門系統維修周期優化研究

李建新 牛 剛

(1.同濟大學鐵道與城市軌道交通研究院，201804，上海；2.中車青島四方機車車輛股份有限公司，266111，青島∥第一作者，工程師)

由于技術條件限制或考慮到制造與運營成本，動車組客室車門系統(以下簡稱“車門系統”)并未安裝大量傳感器用于監控車門系統的健康狀態，所以無法對車門系統的健康狀態進行全面監控與評估。目前，較難對動車組車門系統進行精準狀態維修，預防維修仍然是車門系統維修的主要手段。

當預防維修周期制定不當時，會造成維修不足和維修過剩等，進而會導致次生災害風險和維修成本升高。我國動車組的維修模式參考德國、日本等動車技術起步較早的國家，對我國的路況、運行環境、維修條件等實際情況考慮較少。目前，我國動車組已有十幾年的運行經驗，積累了大量寶貴的檢修、運營等數據，因此有必要根據動車組車門系統歷史故障數據進行FTA(故障樹分析)和FMECA(故障模式影響及危害度分析)分析，找出車門系統的薄弱環節。

本文利用威布爾分布和海因里希法則對車門系統進行可靠性分析。在車門系統可靠性滿足運營要求的前提下，建立了以車門系統單位時間維修費用最低為目標的維修模型。通過對中國鐵路上海局集團有限公司CRH2A型動車組車門維修周期進行優化，驗證了該維修模型的實用性和經濟性，也為動車組其他子系統的維修周期優化提供了借鑒與指導。

1 可靠性分析方法

1.1 FTA和FMECA可靠性分析

FTA是一種圖形演繹方法，將最不希望發生的事件作為頂事件，然后分析可能導致頂事件發生的全部原因。FMECA是一種設計分析方法，其按照一定步驟，通過分析產品各組成部件潛在的故障模式、故障原因及對產品功能的影響，提高產品的可靠性。根據FTA和FMECA可以將CRH2A型動車組車門系統分為5個子系統，這5個子系統可以進一步被分解為23個最小故障單元(即最小可更換單元)。5個子系統分別為：驅動裝置系統、壓緊裝置系統、電氣元器件系統、信號反饋系統和基礎輔助設備系統。

1.2 威布爾分布可靠性特征量

威布爾分布是一種包括3個參數的概率密度分布函數，其3個參數分別為形狀參數α、尺度參數β和位置參數γ[1]。由于車門系統投入運用后隨時可能發生故障，所以選擇兩參數威布爾分布進行分析[2]。可靠性特征量主要包括可靠度函數R(t)(t為設備運行時間)、故障概率密度函數f(t)、累計故障概率密度函數F(t)及故障率函數λ(t)等。可靠度函數R(t)可以表示為：

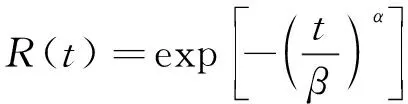
(1)

1.3 威布爾分布參數求解

1.3.1 平均秩次法

由于樣本中存在刪失數據，無法預測這部分數據中的故障時間，此時若直接用近似中位秩公式，往往存在較大誤差。為了提高經驗分布函數精度，平均秩次法是一種較為有效的方法。用平均秩次法求解經驗分布函數的公式為：

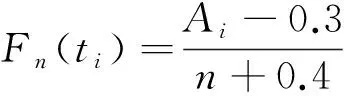
(2)

式中：

i——故障設備順序號;

ti——故障設備i的運行時間，d；

Ai——故障設備i的平均秩次;

n——故障樣本總數，個。

1.3.2 最小二乘法

最小二乘法通過用一條直線擬合離散的數據(xi,yi)(i=1,2,…,r),對威布爾分布進行對數轉換，將其轉換為y=ax+b的形式(a、b為回歸系數)，使計算出的回歸估計值與樣本觀測值之間的偏差最小，計算當∑(yi-a-bxi)2最小時，參數a和b的值。對兩參數威布爾累計分布函數進行變換可得：

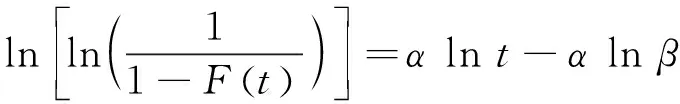
(3)

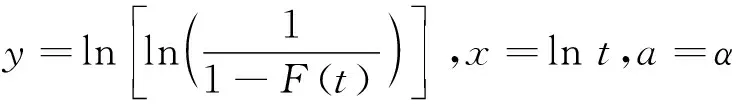
則有：b=-αlnβ

式(3)可以變換為y=ax+b。根據最小二乘法原理，可獲得a和b的最小二乘估計及相關系數rxy，進而獲得α、β。

1.4 經驗分布

根據樣本數據估計出失效分布模型后，需要對所得分布模型與實際分布的擬合程度進行檢驗，常用的檢驗方法有χ2檢驗，K-S檢驗等[3]。其中，χ2檢驗適用范圍更廣，不僅適用于離散型分布和連續型分布的檢驗，也適用于不規則截尾數據。

2 建立維修周期優化模型

2.1 海因里希法則

海因里希通過對事故進行概率統計分析，提出每一起嚴重事故背后都有29起輕微事故及300起沒有造成事故的險情。該理論被稱為海因里希法則。根據海因里希法則，將車門故障按照其影響分為A、B、C 3個等級，A級影響最高，B級次之，C級最弱。故障等級劃分原則如表1所示。由于產品故障多種多樣，影響程度各不相同，因此在可靠性分析領域，一般將不同等級故障進行歸一化處理，按照海因里希法則1…29…300的比例關系[4]，不同故障等級轉換原則如表2所示。

表1 故障等級劃分原則Tab.1 Fault grade classification principle

表2 不同故障等級轉換原則Tab.2 Fault grade conversion principle

2.2 歷史可靠度評估

歷史可靠度Rr指產品在統計期內完成規定功能，而沒有發生C級及以上故障的概率。歷史可靠度計算公式為：

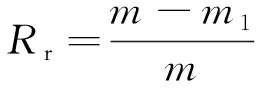
(4)

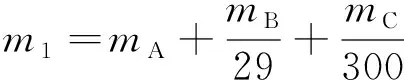
(5)

式中：

m——統計期內產品發生故障的總數量，個；

m1——統計期內可能發生A級故障的數量，個；

mA——統計期內發生A級故障的數量，個；

mB——統計期內發生B級故障的數量，個；

mC——統計期內發生C級故障的數量，個。

2.3 構建優化模型

在制定維修策略時，既不能一味追求可靠性，也不能只追求經濟性，而應該將可靠性與經濟性進行綜合考慮，在追求經濟性的同時要保證可靠性在可接受范圍內。對車門系統維修成本進行優化時，以歷史可靠度作為最低容許可靠度，即R(t)≥Rr。假設車門系統預防維修周期為T，車門系統在單位時間內的維修費用期望損失為C(t)，可以表示為：

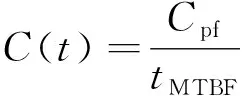
(6)

(7)

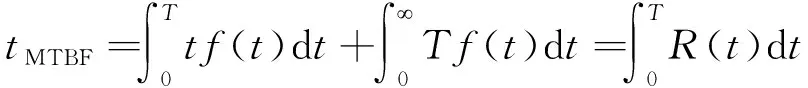
(8)

式中：

Cpf——一個間隔周期內的維修費用期望損失;

tMTBF——一個間隔周期內平均無故障運行時間;

Cp——車門系統進行一次預防維修的費用;

Cf——車門系統進行一次事后維修所需的費用。

每列動車車門系統在單位時間內的維修費用模型可以轉化為：

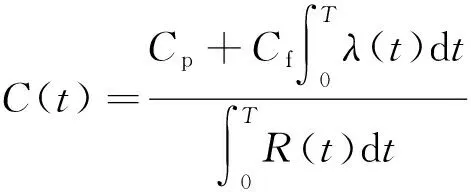
(9)

此時，可將求解最佳維修周期的問題轉換為可靠度在滿足歷史可靠度的條件下，求解車門系統單位時間內的維修費用期望損失最小值的問題。由此可得車門系統最佳維修周期模型為：

s.t.R(t)≥Rr

(10)

3 實例分析

3.1 威布爾分布參數計算

選取中國鐵路上海局集團有限公司2016年1月—2019年12月的5列CRH2A型動車組客室車門系統故障數據，有效故障條數為679條，刪失故障條數為39條。利用平均秩次法及最小二乘法求解威布爾分布參數。平均秩次法及其經驗分布函數取值如表3所示。

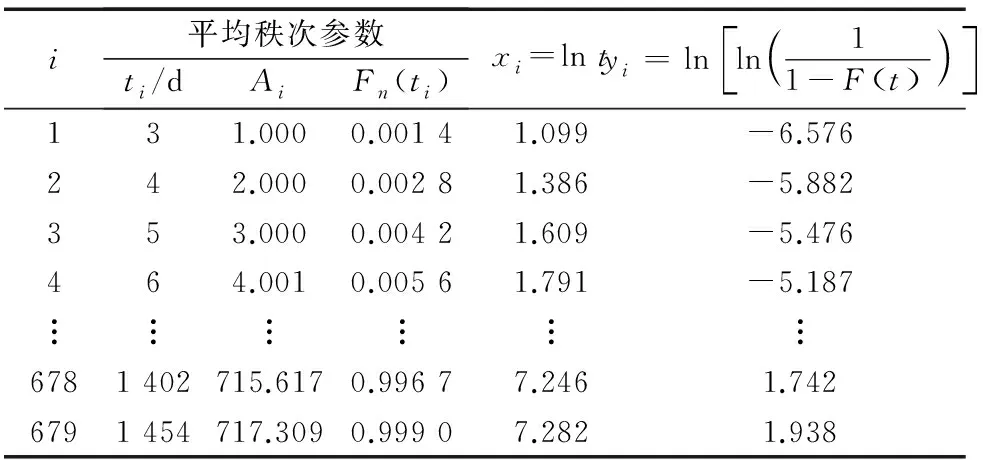
表3 平均秩次法及其經驗分布函數取值

采用最小二乘法對利用平均秩次法求得的車門系統各故障時間離散點數據(xi,yi)進行擬合，根據擬合直線可以獲得回歸系數a(斜率)和b(截距)，以及95%置信區間和線性相關系數rxy。最小二乘法擬合數據相關參數如表4所示。由表4可知，威布爾分布中α為1.331，β為282.132。最小二乘法擬合仿真圖如圖1所示。由圖1可知，rxy=0.993 6，當rxy越接近于1時說明回歸直線擬合得越好。則車門系統可靠度函數R(t)=exp[-(t/282.132)1.331]，故障率函數λ(t)=1.331t0.331/282.1321.331。

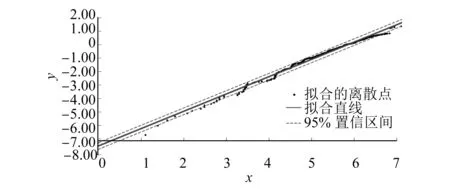
圖1 最小二乘法擬合仿真圖Fig.1 Diagram of least squares method fitting simulation

表4 最小二乘法擬合數據相關參數表

3.2 威布爾分布擬合優度檢驗

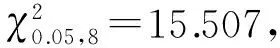
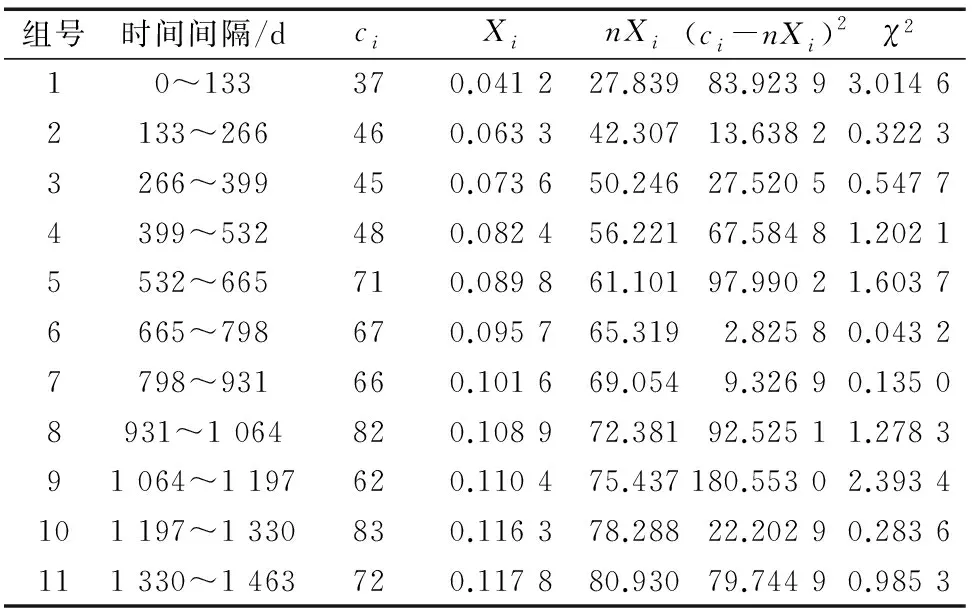
表5 故障分布模型χ2檢驗Tab.5 χ2 verification of fault distribution model

3.3 車門系統最佳維修周期

根據海因里希法則劃分車門系統故障等級。據統計，車門系統故障總數為679條，其中，A級故障81條，B級故障194條，C級故障404條。由此計算可得，統計期內A級故障數為89.036，歷史可靠度為0.869。

根據調研，中國鐵路上海局集團有限公司CRH2A型動車組車門系統的預防維修費用為500元，事后維修費用為1 500元。將車門系統的故障率函數、可靠度函數、Rr=0.869、Cp=500元、Cf=1 500元代入維修周期優化模型，可得：

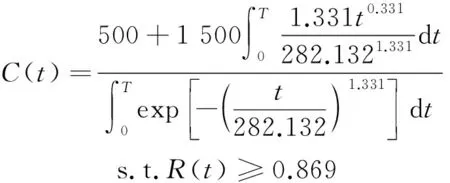
(11)

對上述目標函數進行求解。為更直觀地表現最佳維修模型，繪制單位時間維修費用期望損失函數及可靠度函數曲線，如圖2和圖3所示。由圖2可知，單位時間維修費用期望損失隨時間先降低后升高，即：維修周期小于159 d時的維修費用期望損失單調遞減；維修周期大于159 d時的維修費用期望損失單調遞增；若不考慮系統可靠度，當維修周期為159 d時，維修費用有最小值。由圖3可知，當R(t)=0.869時,T=65 d，即維修周期在(0,65]區間才能滿足R(t)≥0.869的條件。而單位時間維修費用期望損失函數在維修周期小于65 d時也是單調遞減的，因此可獲得車門系統最佳維修周期為65 d。

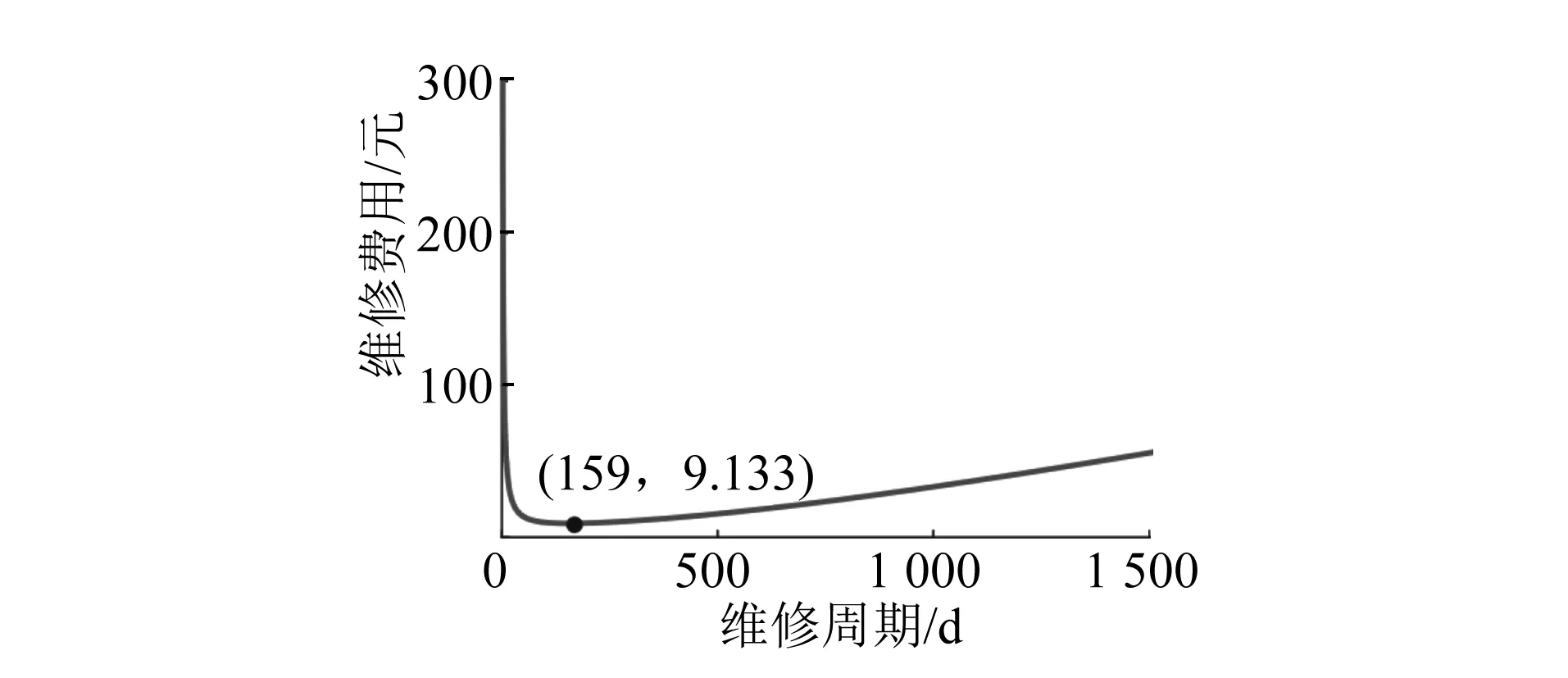
圖2 單位時間維修費用期望損失曲線Fig.2 Expected loss curve of maintenance cost per unit time

圖3 可靠度函數曲線Fig.3 Reliability function curve

3.4 結果分析

當維修周期為65 d時，一個維修周期單位時間內的維修費用期望損失為11.6元/d，而優化后的一個維修周期內的維修費用期望損失為754元。目前，動車組車門系統的維修周期為30 d，一年維修12次。當維修周期為30 d時，平均每天維修期望損失為19.6元/d，以一個月為周期的維修費用為588元。不同維修間隔時，單位時間內的維修期望損失如圖4所示。

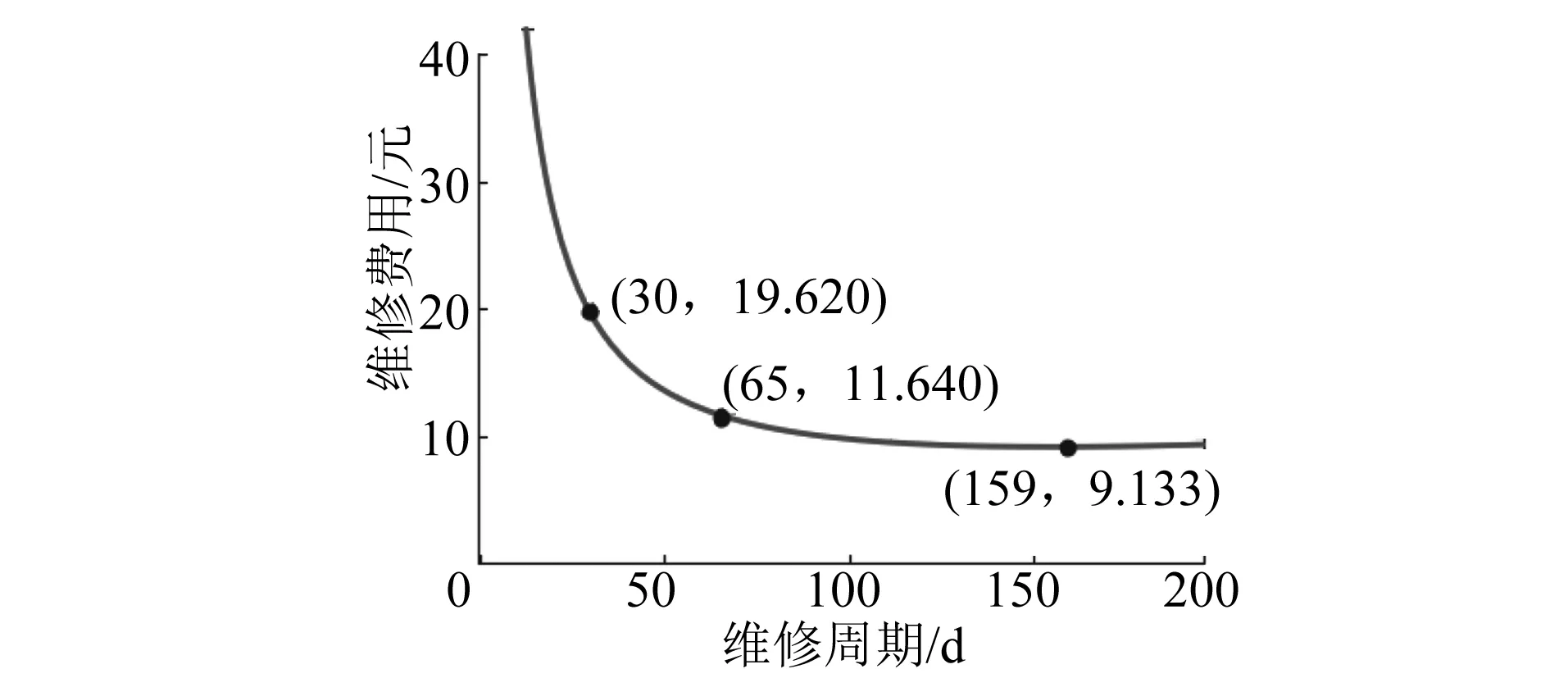
圖4 不同維修間隔下單位時間內的維修費用期望損失

維修周期優化后，每列車每年的客室車門系統維修費用約為4 524元，而維修周期優化前每列車每年的客室車門系統維修費用約為7 056元。維修周期優化后，在保證車門系統可靠性不變的情況下，每列車每年的維修成本降低了1/3。

4 結語

基于動車組車門系統故障間隔服從威布爾分布，建立了以歷史可靠度為約束條件、車門系統單位時間維修費用最低為目標的維修模型。以中國鐵路上海局集團有限公司CRH2A型動車組車門系統實例進行分析，在保證車門系統可靠性滿足運行要求的情況下，車門系統維修周期由30 d優化為65 d，維修費用降低了1/3，大大降低了車門系統的維修費用，驗證了維修模型的實用性和經濟性。