Navier-Stokes方程的二階解耦BDF格式的穩(wěn)定性和收斂性分析
牟小鳳,夏澤宇,李茂軍
(電子科技大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,成都 611731)
不可壓粘性Navier-Stokes方程是流體運(yùn)動(dòng)模擬的基本問(wèn)題之一,其數(shù)學(xué)理論以及數(shù)值解是非常重要的研究領(lǐng)域。本文考慮下列定常不可壓Navier-Stokes方程:
ut-μΔu+u·?u+?p=0,x∈Ω,t∈(0,T],
(1)
?·u=0,x∈Ω,t∈(0,T],
(2)
u=0,x∈?Ω,t∈(0,T],
(3)
u(·,0)=u0,x∈Ω,
(4)
在過(guò)去的幾十年里,已經(jīng)有許多工作致力于不可壓Navier-Stokes方程的理論研究和數(shù)值分析。從Girault和Raviart的專著[1]中可以看到關(guān)于Navier-Stokes方程的數(shù)學(xué)理論和數(shù)值算法。對(duì)于Navier-Stokes方程數(shù)值方法的穩(wěn)定性和收斂性的研究,Codina和Blasco[2-3]設(shè)計(jì)了穩(wěn)態(tài)Stokes方程的穩(wěn)定數(shù)值格式,并將其推廣到了非線性Navier-Stokes方程;Nochetto和Pyo[4]提出了一個(gè)關(guān)于Navier-Stokes問(wèn)題的數(shù)值格式,并分析了該格式無(wú)條件穩(wěn)定性;He[5]對(duì)Navier-Stokes方程提出了一種完全離散的懲罰有限元方法,并給出了最優(yōu)誤差估計(jì)。另外還有許多其他關(guān)于Navier-Stokes方程數(shù)值格式的穩(wěn)定性和誤差分析的工作,如文獻(xiàn)[6-7]及其參考文獻(xiàn)。這些離散格式大多是非對(duì)稱格式,而有些學(xué)者則通過(guò)解耦的技巧使方程對(duì)稱化。Shen[8]對(duì)非定常不可壓Navier-Stokes方程解耦格式進(jìn)行了嚴(yán)格的誤差分析。Shen和Yang[9]提出了兩相不可壓流相場(chǎng)模型的解耦格式,并證明了該格式的無(wú)條件能量穩(wěn)定性。Mu和Zhu[10]提出了Stokes/Darcy流問(wèn)題的解耦有限元格式,此結(jié)果被推廣到不同域的不同時(shí)間步長(zhǎng)[11]。基于Crank-Nicolson(CN)方法和FEM,一種能量穩(wěn)定且唯一可解的求解磁流體方程的解耦格式在文獻(xiàn)[12]中被提出,該文首次使用引入中間映射來(lái)證明不可壓磁流體的最優(yōu)收斂速率。針對(duì)不可壓Navier-Stokes方程解耦格式的研究還有很多,如文獻(xiàn)[13]。二階BDF法作為常微分方程的時(shí)間離散方法得到了廣泛的應(yīng)用[14]。二階BDF格式具有穩(wěn)定性強(qiáng)、精度高等優(yōu)點(diǎn),成為目前常用的多步方法之一。
本文采用常規(guī)的半隱半顯技巧對(duì)非線性移流項(xiàng)u·?u進(jìn)行了線性化處理,進(jìn)而得到了線性的離散系統(tǒng)。盡管已經(jīng)有許多工作致力于不可壓Navier-Stokes方程的穩(wěn)定性分析,但是通過(guò)添加時(shí)間步長(zhǎng)平方階的修正項(xiàng),首次對(duì)二階BDF解耦格式求解Navier-Stokes方程進(jìn)行了嚴(yán)格的無(wú)條件能量穩(wěn)定性的證明。能量穩(wěn)定性結(jié)合線性確保了離散系統(tǒng)對(duì)應(yīng)的齊次方程組只有零解,進(jìn)而得到了方程的唯一可解性。在最優(yōu)誤差分析中,通過(guò)利用文獻(xiàn)[12]中證明不可壓磁流體方程的技巧,即引入中間映射并給出相應(yīng)估計(jì),也是首次使用該方法完成了對(duì)二階BDF解耦格式解Navier-Stokes方程的最優(yōu)收斂速率的證明。本文得到了速度場(chǎng)在L∞([0,T],L2)范數(shù)下的最優(yōu)收斂階(τ2+hr+1),其中r表示多項(xiàng)式函數(shù)空間的次數(shù),h和τ分別表示空間網(wǎng)格尺寸和時(shí)間步長(zhǎng)。最后提供算例驗(yàn)證本文所證明的格式的性質(zhì)。
1 變分形式
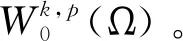
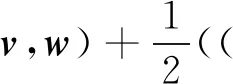
(5)
b(u,v,w)=-b(u,v,w),b(u,v,v)=0。
(6)
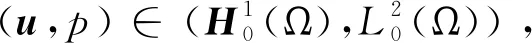
(ut,v)+μ(?u,?v)+b(u,u,v)-(p,?·v)=0,
(7)
(?·u,q)=0。
(8)
2 全離散格式和穩(wěn)定性
2.1 數(shù)值離散
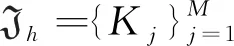
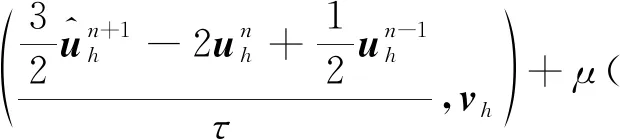
(9)

(10)
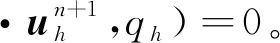
(11)

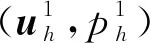
2.2 能量穩(wěn)定性
本節(jié)主要證明全離散格式(9)—(11)的無(wú)條件能量穩(wěn)定性。需要定義如下離散梯度算子?h∶Mh→Xh:
(vh,?hqh)=-(?·vh,qh),?(vh,qh)∈(Xh,Mh)。
(12)
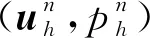
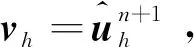
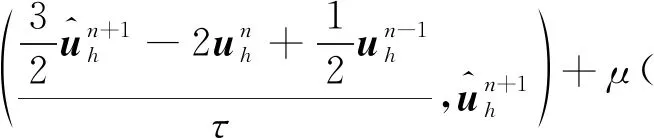
(13)
根據(jù)
(14)
以及三線性形式的性質(zhì)(6),消去非負(fù)項(xiàng)后可以將式(13)化為

(15)
(16)
(17)
(18)
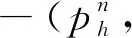
(19)
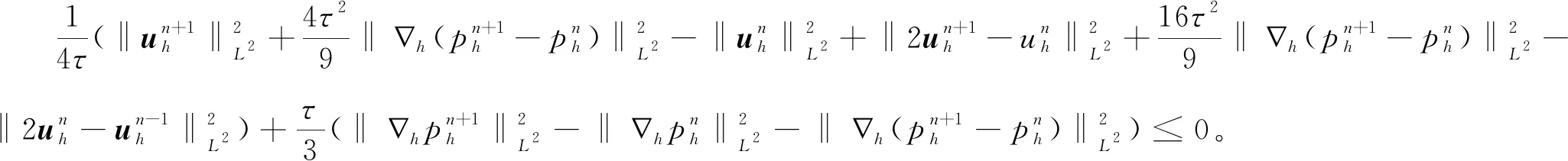
綜上所述,定理1得證。
3 最優(yōu)誤差估計(jì)
本節(jié)主要分析全離散格式(9)—(11)的最優(yōu)收斂速率。先進(jìn)行正則性假設(shè):
‖uttt‖L∞(0,T;L2)+‖utt‖L∞(0,T;H1)+‖ut‖L∞(0,T;Hr+1)+‖u‖L∞(0,T;Hr+2)+‖ptt‖L∞(0,T;L2)+‖pt‖L∞(0,T;Hr+1)≤M。
(20)
3.1 預(yù)備知識(shí)
為了估計(jì)二階解耦BDF-FEM所得近似解的誤差,本節(jié)將引入一些重要的投影算子和已有的結(jié)論。
定義L2投影算子Ph:L2(Ω)→Mh(或L2(Ω)→Xh)為:
(Phv,qh)=(v,qh), ?(v,qh)∈(L2(Ω),Mh)(或(v,qh)∈(L2(Ω),Xh))。
(21)

(22)
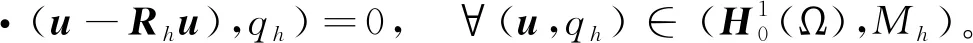
(23)
由參考文獻(xiàn)[15-16]可知,L2投影算子和Stokes投影算子有如下性質(zhì)。
引理1針對(duì)(21)中定義的L2投影算子和(22)—(23)中定義的Stokes投影算子,其滿足如下估計(jì):
對(duì)于n=0,1,0≤l≤r,1≤q≤∞有
‖Phv‖Wn,q≤C‖v‖Wn,q,
(24)
‖v-Phv‖L2≤Chl+1‖v‖Hl+1。
(25)
對(duì)于0≤l≤r,1 ‖u-Rhu‖Lq+h‖u-Rhu‖Wl,q≤Chl+1(‖u‖Wl+1,q+‖p‖Wl,q), (26) ‖u-Rhu‖Lq+h‖u-Rhu‖Wl,q≤Chl+1(‖u‖Wl+1,q+‖p‖Wl,q), (27) ‖p-Rhp‖Lq≤Chl(‖u‖Wl+1,q+‖p‖Wl,q), (28) ‖?t(u-Rhu)‖Lq+‖?t(p-Rhp)‖Lq≤Chl+1(‖?tu‖Wl+1,q+‖?tp‖Wl,q)。 (29) 其中所有的C都是不依賴于h的正常數(shù)。 此外,引入文獻(xiàn)[17]中的如下逆不等式。 引理2存在不依賴于h的正常數(shù)C,使得對(duì)于所有的uh∈Mh,Xh滿足下面的估計(jì) (30) 其中d表示空間的維數(shù)。 根據(jù)離散梯度算子?h在(12)中的定義與文獻(xiàn)[12],給出如下引理3和引理4。 引理3對(duì)于所有qh∈Mh,有 ‖?hqh‖L2≤Ch-1‖qh‖L2, (31) 其中C是不依賴于h的正常數(shù)。 引理4如果正則性假設(shè)(20)成立,則滿足 ‖?hPh?tp-Ph??tp‖L2≤Ch, (32) 其中C是不依賴于h和τ的正常數(shù)。 引理5如果正則性假設(shè)(20)成立,則滿足 ‖?h(Rhpn+1-Rhpn)‖L2≤Cτ, (33) 其中C是不依賴于h和τ的正常數(shù)。 證明利用正則性假設(shè)可知 ‖?h(Rhpn+1-Rhpn)‖L2=Cτ‖?hRh?tpn+1‖L2(利用泰勒展開(kāi))≤Cτ(‖?hRh?tpn+1-?hPh?tpn+1‖L2+‖?hPh?tpn+1-Ph??tpn+1‖L2+‖Ph??tpn+1‖L2)≤Cτ(Ch-1‖Rh?tpn+1-?tpn+1‖L2+Ch-1‖?tpn+1-Ph?tpn+1‖L2+Ch+C)(利用(24)和(32))≤Cτ(Ch-1Ch2+Ch-1Ch2+Ch+C) (利用(25)和(28))≤Cτ。 綜上所述,此引理得證。 (34) 上式可以等價(jià)的寫(xiě)為下面的形式:對(duì)于所有rh∈Xh,有 (35) 因此,結(jié)合上面定義的變量和函數(shù),以及利用3.1節(jié)中定義的投影算子,變分形式(7)—(8)可以轉(zhuǎn)化為:對(duì)于所有(vh,qh)∈(Xh,Mh)和n=1,2,…,N-1,有 (36) (?·Rhun+1,qh)=0, (37) 對(duì)于所有(vh,rh,qh)∈(Xh,Xh,Mh)和n=1,2,…,N-1,誤差函數(shù)滿足 (38) (39) (40) 基于3.2節(jié)中的討論,針對(duì)所提出的二階解耦算法,有如下的最優(yōu)誤差估計(jì)。 (41) 其中C0是一個(gè)不依賴于τ和h的正常數(shù)。 (42) (43) (44) (45) ≤C(T2+hr+1)2+ (46) 估計(jì)式(46)中第一行右端的第一項(xiàng)‖?(?hRhpn+1-?hRhpn)‖L2可以被以下不等式控制 ‖?(?hRhpn+1-?hRhpn)‖L2 =Cτ‖?(?hRh?tpn+1)‖L2(利用泰勒展開(kāi)) ≤Cτ(‖?(?hRh?tpn+1-?hPh?tpn+1)‖L2+‖?(?hPh?tpn+1-Ph??tpn+1)‖L2)+Cτ‖?(Ph??tpn+1)‖L2 ≤Cτ(Ch-2‖Rh?tpn+1-Ph?tpn+1‖L2+Ch-1‖?hPh?tpn+1-Ph??tpn+1‖L2)+Cτ‖??tpn+1‖H1(利用(24)和(31)) ≤Cτ(Ch-2‖Rh?tpn+1-?tpn+1‖L2+Ch-2‖?tpn+1-Ph?tpn+1‖L2+Ch-1Ch1)+Cτ(利用(32)) ≤Cτ(Ch-2Ch2+Ch-2Ch2)+Cτ(利用(25)和(28))≤Cτ, 其中正則性假設(shè)(20)被多次使用。注意到(34),因此有 (47) (48) (49) 利用等式(39)和(40),還可以得到 (50) (51) 然后將以上估計(jì)(45)—(51)代入不等式(44)的兩端,整理可得 (52) 時(shí)也成立。最后,利用三角不等式,投影誤差估計(jì)(27)和估計(jì)(52)即得結(jié)論(41),完成了定理2的證明。 本小節(jié)中,以有限元軟件FreeFem++為平臺(tái)進(jìn)行編程,通過(guò)數(shù)值算例來(lái)檢驗(yàn)二階解耦BDF-FEM數(shù)值格式的精度。為了方便起見(jiàn),本文考慮在區(qū)域Ω×[0,T]=[0,1]×[0,1]×[0,1]上滿足Dirichlet邊界條件(3)和初始條件(4)的不可壓Navier-Stokes方程: ut-μΔu+u·?u+?p=f,x∈Ω,t∈(0,T], (53) ?·u=0,x∈Ω,t∈(0,T], (54) 其中μ=0.1,以及源項(xiàng)f對(duì)應(yīng)于如下真解: 采用全離散解耦格式(9)—(11)求解Navier-Stokes方程(53)—(54)。在實(shí)驗(yàn)中,有限元離散使用二次元逼近u以及線性元逼近p。為了驗(yàn)證時(shí)間誤差收斂階(τ2),選擇足夠小的空間網(wǎng)格尺寸h=1/100使得空間離散誤差可以忽略不計(jì),并取時(shí)間步長(zhǎng)τ=1/10,1/20,1/40,1/80,在T=1處的時(shí)間誤差和收斂階見(jiàn)表1:速度u在L2范數(shù)下的誤差隨時(shí)間步長(zhǎng)τ的逐漸減小而降低,說(shuō)明在時(shí)間上數(shù)值方法是收斂的。數(shù)值結(jié)果也驗(yàn)證了時(shí)間誤差分析得到的二階收斂速度,這與定理2中的理論分析保持一致。類似地,為了驗(yàn)證空間精度的收斂階,固定τ=1/10000,并且選擇逐漸減半的的空間網(wǎng)格尺寸h=1/10,1/20,1/40,1/80,得到在T=1處相應(yīng)的數(shù)值結(jié)果如表1所示:誤差隨著空間網(wǎng)格尺寸h的減小而降低,并且空間收斂速度與定理2中理論預(yù)測(cè)一致,保持三階的收斂階。 表1 二階解耦BDF-FEM的誤差和收斂階 為了驗(yàn)證所提算法的有效性,采用有限元方法求解二維Navier-Stokes方程,對(duì)雷諾數(shù)Re=100的二維圓柱繞流進(jìn)行數(shù)值模擬。針對(duì)不可壓縮粘性流體,其運(yùn)動(dòng)規(guī)律可以用Navier-Stokes方程來(lái)描述,我們考慮在區(qū)域Ω×[0,T]=[-1,1]×[-0.3,0.3]×[0,10]上的控制方程: 一個(gè)直徑D=0.2 m且無(wú)窮長(zhǎng)的圓柱體,放置在無(wú)窮遠(yuǎn)來(lái)流速度為1.0 m·s-1,不受干擾的均勻橫流中。計(jì)算區(qū)域大小為上游邊界距圓柱圓心為2.5D,下游邊界距圓柱圓心7.5D,頂部和底部邊界均距圓柱圓心1.5D。選取固定空間網(wǎng)格尺寸h=1/80和時(shí)間步長(zhǎng)τ=1/100。雷諾數(shù)Re由圓柱體直徑D和自由來(lái)流速度U確定:Re=ρUD/μ,其中ρ表示流體密度,μ表示動(dòng)力粘度。經(jīng)過(guò)上述的網(wǎng)格劃分和參數(shù)設(shè)置,模擬雷諾數(shù)為100時(shí)的繞流流動(dòng),得到的渦量圖如圖2所示。從圖中可以觀察出,圓柱上下游的流線逐漸不具有對(duì)稱性。 本文針對(duì)不可壓Navier-Stokes問(wèn)題,基于時(shí)間離散的二階BDF和Taylor-Hood有限元空間離散,提出了相對(duì)應(yīng)的解耦算法,并對(duì)解耦算法進(jìn)行了理論分析與數(shù)值模擬,證明了數(shù)值格式的無(wú)條件能量穩(wěn)定性和唯一可解性,并進(jìn)一步嚴(yán)格地給出了最優(yōu)收斂階。最后,通過(guò)數(shù)值實(shí)驗(yàn)驗(yàn)證了該方法求解Navier-Stokes問(wèn)題的精度、無(wú)條件能量穩(wěn)定性以及算法的有效性。本文首次對(duì)二階解耦BDF格式求解Navier-Stokes方程進(jìn)行了嚴(yán)格的穩(wěn)定性證明。在最優(yōu)誤差估計(jì)證明中,引入中間映射算子的技巧可以被推廣到其他有中間變量的格式中用于理論分析。在將來(lái)的工作中會(huì)將解耦格式及其理論分析應(yīng)用于更復(fù)雜的模型。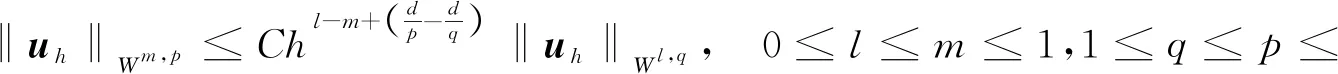
3.2 誤差方程
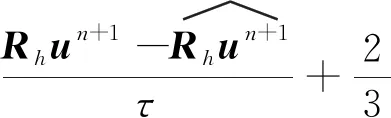
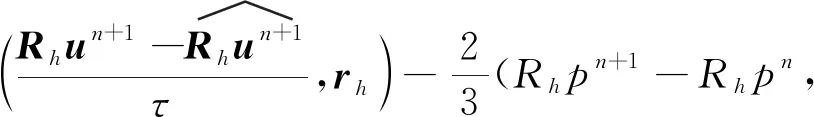
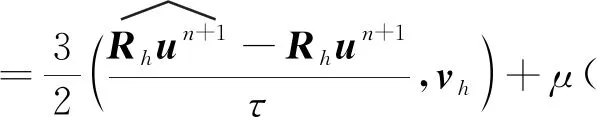

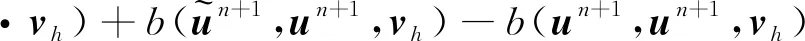
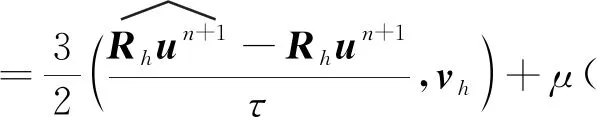
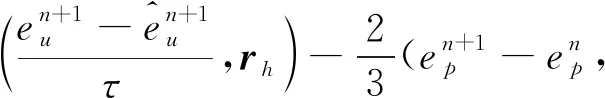
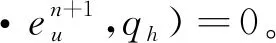
3.3 最優(yōu)誤差估計(jì)
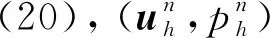
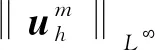

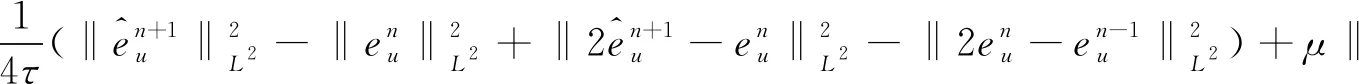
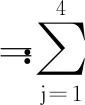
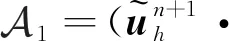
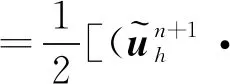
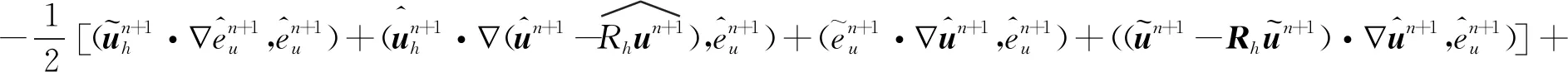
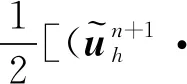
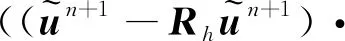
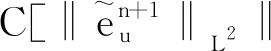
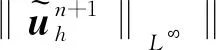
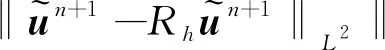
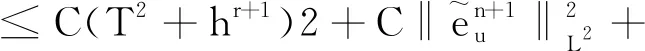
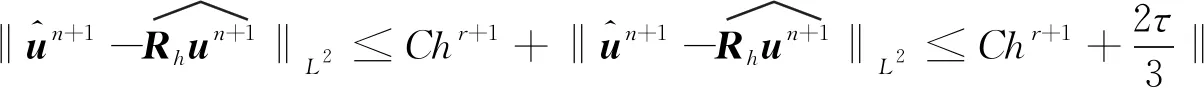
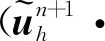
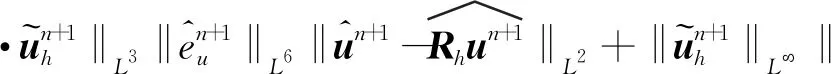
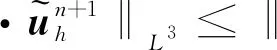
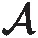
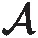
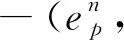
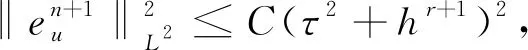
4 數(shù)值算例
4.1 算例1
4.2 算例2


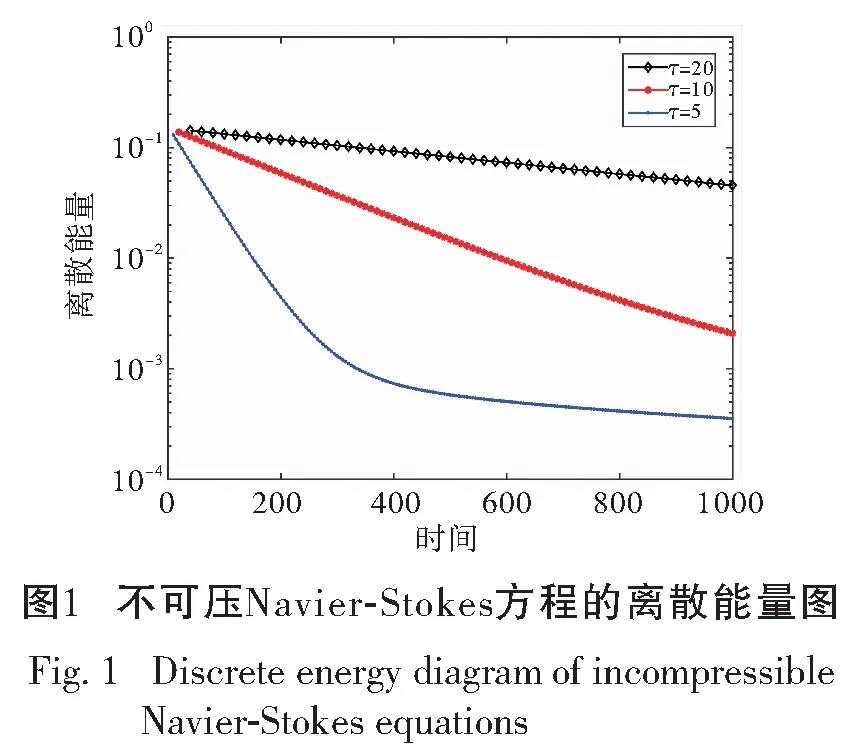
4.3 算例3

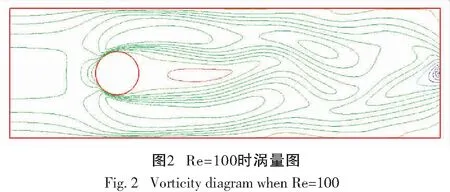
5 結(jié)論與展望
 西華師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2023年1期
西華師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2023年1期
- 西華師范大學(xué)學(xué)報(bào)(自然科學(xué)版)的其它文章
- 高師學(xué)報(bào)自科期刊影響力提升的困境與策略
——以《西華師范大學(xué)學(xué)報(bào)(自然科學(xué)版)》為例 - 四川省屬師范院校中國(guó)地理課程思政教學(xué)路徑探索
- 南充市旅游業(yè)與人居環(huán)境耦合協(xié)調(diào)研究
- 大熊貓國(guó)家公園映秀鎮(zhèn)典型受損滑坡體土壤理化性質(zhì)與植被恢復(fù)初探
- 佛坪保護(hù)區(qū)冬季大熊貓犬瘟熱病毒的預(yù)防與監(jiān)測(cè)措施
- 從一個(gè)四維左對(duì)稱代數(shù)構(gòu)造一些八維相空間
