采用干涉條紋紋影法的軸對稱溫度場測量

吳軍，宋豐成，潘智祥，張琛萍，郭潤夏，張曉瑜

（1.中國民航大學 航空工程學院，天津 300300；2.中國民航大學 電子信息與自動化學院，天津 300300）

1 引言

航空發動機的運行狀態監測在飛行安全領域發揮著重要作用［1-2］。在航空發動機工作時，尾氣產生的溫度場中蘊含著大量關于發動機燃燒狀態的信息［3-4］。這些狀態信息都可以對發動機運行狀態控制提供理論依據與數據支持［5-6］。以航空發動機的尾氣為例，根據火焰燃燒特性，溫度分布按照中心對稱并沿著空氣流動方向逐漸降低形成三維溫度場，采取接觸式測溫會破壞流場結構，影響溫度測量，現階段常用光學測量法通過測量空氣折射率分布實現非接觸式測溫［7］。激光吸收光譜測溫法是利用光在散射后發生能量衰減來對溫度測量［8-10］，常適用于需要搭建大量測量結構的溫度場截面測量，在尾氣流場這樣溫度場測量中受到限制。

現代定量紋影測量技術由 Moreno-Hernández［11］提出，具有精度高，可視化效果好等優點。紋影系統結構近似為傅里葉光學處理器，使用刀口充當了空間頻譜的半平面掩模，對通過待測流場的平行光束實現空間濾波，可以顯示出折射率場中的紋影細節［12］。這一方法受到透鏡尺寸的影響，一般測量范圍在15 cm 左右，多用于實驗室內測量。2013 年Martinez-Gonzalez［13］采用定標紋影法測量了加熱金屬板引起的空氣自然對流中的溫度場，2017 年，Alvarez-Herrera［14］通過改良紋影技術完成了發動機內部溫度場重建。

反射式紋影技術，是20 世紀中期提出的一種將高速相機與反光屏幕和紋影技術相結合的簡易紋影法。該方法早期被應用在航空彈道學和直升機旋翼的測試分析中，現在與高速相機攝像、反光屏幕等相結合進行紋影測量［15］。2017 年Gihyeon Min［16］在實驗室條件 下用此方法對 蠟燭、沸騰熱水壺、加熱器和燃氣火炬引起的空氣湍流進行了成像。經過亮度補償后，干涉精度對比原始紋影精度平均提高14.15 倍。2018 年，Martinez-Gonzalez［17］利用此方法設計了一種測量流體平面溫度場的方法，并測量了商業熱風槍焊接時噴嘴發出的熱空氣平面溫度場。可以看出，與激光診斷技術［18］相結合的光學測量方法在溫度測量方面具有更高的工程應用價值。結合二者優點的紋影測溫方法具有非接觸測量、對測量結果響應速度快和空間分辨率高的優勢。由于傳統的背景紋影法的局限性是測量范圍基于相機的成像模型，不可避免存在圖像畸變，而邊緣位置圖像偏移量本身較小，會導致整體測量精度的下降。本文結合紋影成像模型和激光干涉測溫等原理，提出了利用干涉條紋光程差解算折射率分布的方法。該方法在保留背景紋影法測量設備簡單的基礎上，極大地提高了測量的穩定性與精確性。由于激光干涉條紋對折射率場變化敏感且有良好的相干性，因此產生的干涉條紋可以放大光線偏折角，進而有效提高紋影法溫度測量精度。

2 干涉條紋紋影軸對稱溫度場測溫原理

2.1 干涉條紋的形成及變形原理

條紋背景紋影法，是利用光線在通過固定狹縫后會發生的干涉現象對固定場內影響折射率分布因素的測量。

楊氏雙縫干涉實驗的條紋產生原理如圖1 所示。相干光源S1和S2由單色點光源S垂直射到相鄰的兩個小孔上，此時兩個小孔就相當于兩個同相位的次級光源，光束在xOy平面上的成像區域疊加會產生條紋圖樣。這種干涉條紋是由強度相同，相位不同的光干涉產生的。

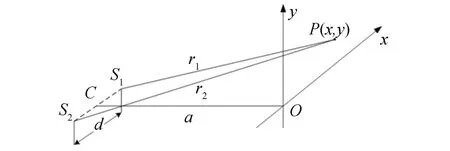
圖1 兩個點光源產生干涉的幾何圖示Fig.1 Geometric diagram of interference from a set of coherent light sources

設定干涉圖樣存在xOy平面上，該平面與S1S2的垂直等分線CO正交，且x軸平行于S1S2。假設兩個小孔的間隔d相對于兩孔連線到觀察面的距離a很小，對于點成像平面上的P（x，y）而言，存在路徑關系：

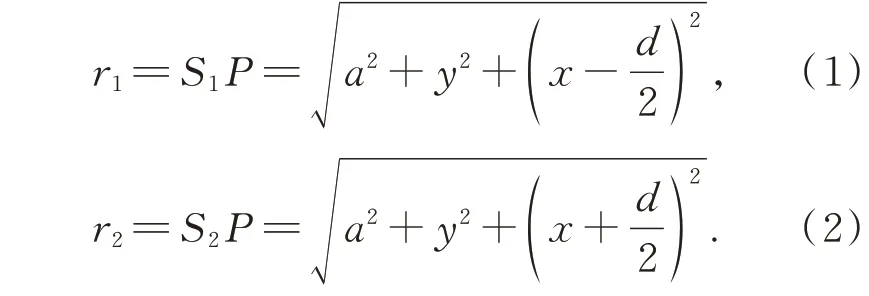
得到實際路徑差：

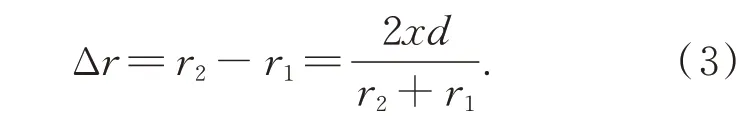
根據溫度場的變化，r1與r2路徑上的折射率值發生改變，同一位置在溫度場存在前后的光程差主要受到溫度影響，從而改變相位差。在不考慮折射率變化的情況下有相位差關系：

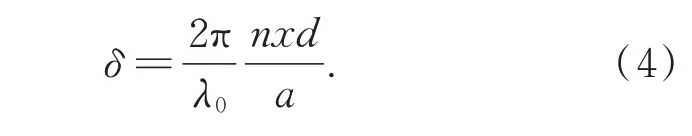
由于光在非均勻折射率場中傳播時會受到介質的折射率影響改變傳播速度，相干光源在經過特定的區域后，產生的相位差會發生變化。由于干涉條紋本身具有尺度的特性，在固定位置的紋影測量實驗中，使用條紋干涉紋影測量的方法能夠得到條紋偏移的真實距離，從而解算相位差。

條紋是根據相干光源疊加產生的，即等波長，相同傳播方向，不同相位的光線疊加，可以看作兩個振幅為a1的矢量波E1和E2的疊加：

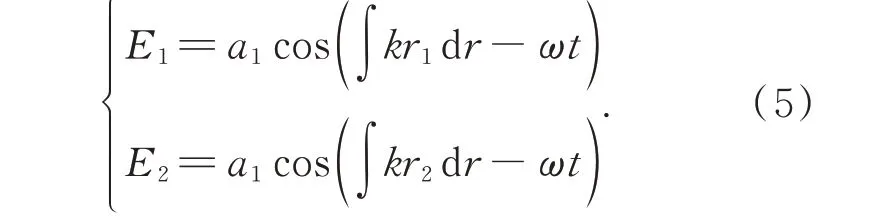
其中：ωt由于光源波長相同，頻率一致，∫krdr為光線經過高溫區域產生的相位變化值。

直接通過匹配光強條紋的偏移求得條紋偏移量，進而推出相位差的變化。相干光的相位變化值，可以得到光程差變化量，進而得到光路直線上折射率值的積分。

2.2 基于干涉條紋變形的軸對稱溫度場重構

在理想狀態下，火焰溫度場呈軸對稱均勻分布。因此當火焰處于測量位置中心時，受到溫度影響的光線折射率分布也均勻軸對稱，從各個視角得到的紋影圖像結果相同。假設火焰滿足理想溫度分布條件，就可以利用一個角度的測量信息反解出火焰的三維溫度場分布。

對于軸對稱的介質而言，Abel 反演公式可以實現從一維投影場重建二維平面結果。構建一個高斯分布的折射率場n，則有光線通過的積分路徑如圖2 所示。高斯分布的折射率場，有距離中心距離相同處折射率相同的對稱特點，由于相干光線位置接近，實際產生的相位差等價于由不同的積分半徑造成的積分差，其中r表示被測平面任意位置的軸向半徑，R表示測量區域內的最大軸向半徑。

圖2 光線通過軸對稱折射率場的相位差積分原理Fig.2 Principle of phase difference integration of light through an axisymmetric refractive index field

根據干涉條紋的產生性質，相位差是光程差與光頻率的關系，當光線穿過軸對稱折射率場時，由于光線的偏折角極小，在x處產生的相位差δ可以根據公式（8）計算：

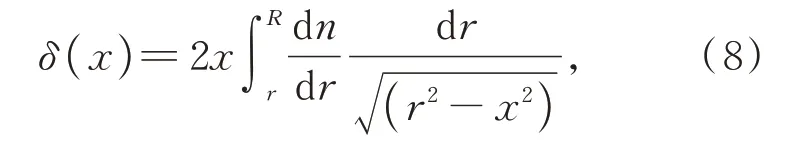
其中的變量n為歸一化折射率，即以測試場周圍環境折射率為1 等比例求解的折射率分布。此歸一化的折射率n分布可以由Abel 逆變換求得：

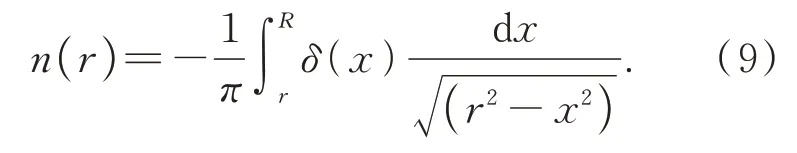
根據此公式求解積分函數時會存在奇點問題，因此求解時采用數值近似方法求解。設定兩束相干光線的距離固定，且相干光線相鄰兩段Δr=rj-ri的相位差變化量為δj，積分得到n（ri）為不同位置的折射率梯度。變量i和j表示光線發生偏折區域的順序數據點，即積分路徑上的順序。線性算子系數Dij與相干光線間距Δr無關系，利用反演算法可以確定：

將式（10）帶入變換公式中，利用辛普森1/3rd進行求解：

帶入得到線性算子系數Dij：

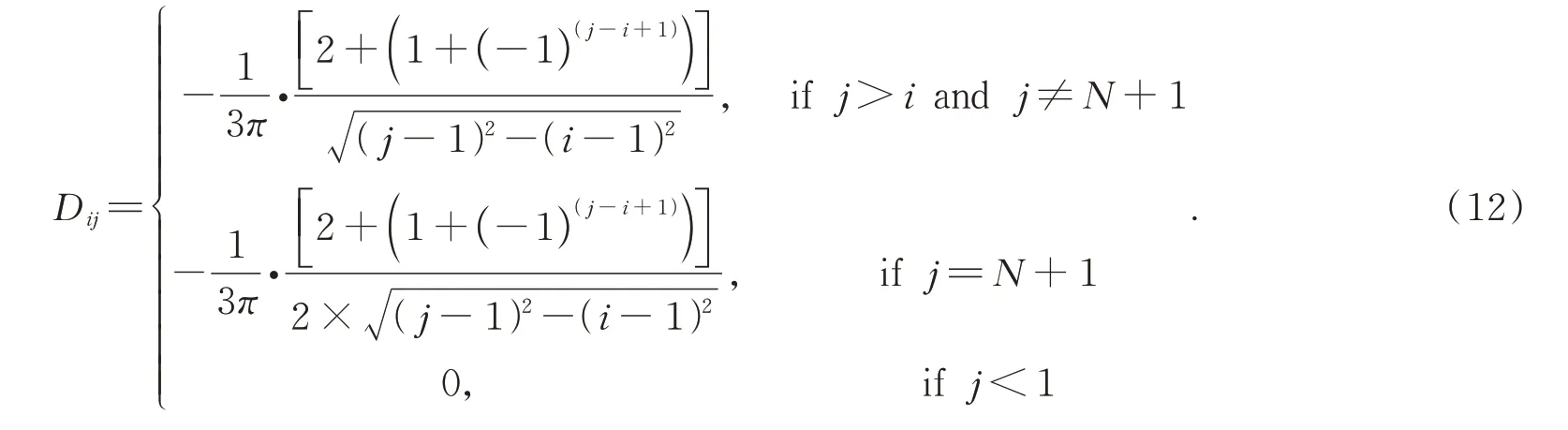
通過Dij外推后，可以得到消除i=j處的奇點，得到結果：

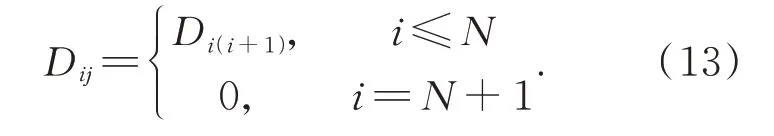
此時得到的Dij為相位變化值與折射率之間的關系。其中，1 標準大氣壓下，波長為644 nm的可見光在15 ℃且CO2含量450 ppm 的干燥空氣中折射率是1.000 276 4。空氣中光的折射率n受到傳播介質的溫度、密度以及光線的波長等條件限制，對于光線的折射率計算存在眾多經驗公式，符合實驗室環境條件選取了Ciddor 公式［19］。將水蒸氣含量百分比e=0，大氣壓P=101 325 Pa，光波長λ=0.54 μm，帶入可以得到空氣的折射率與溫度之間的反比關系：

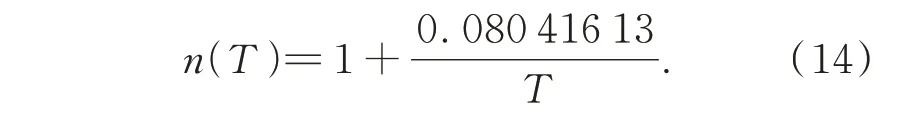
2.3 條紋系統對溫度場重構的影響

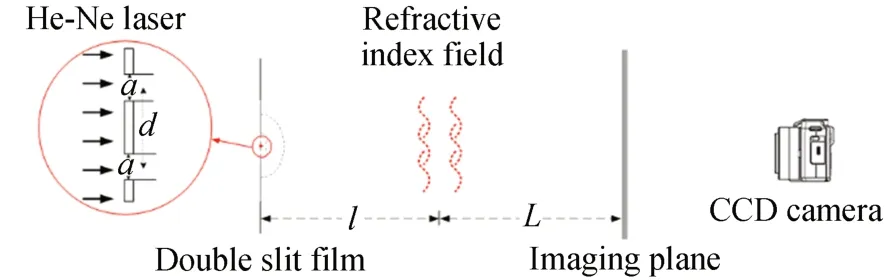
圖3 狹縫對于條紋影響示意圖Fig.3 Diagram of the effect of slits on stripes

因為條紋圖案是根據雙縫干涉產生的，條紋間距反應了光程差的信息。在系統構型固定的情況下，條紋變化就可以反映該測量空間內空氣折射率的變化信息，因此在固定系統構型時需要充分考慮干涉條紋的影響。由于激光干涉的特殊性質，在衍射光線夾角超過6°后，得到的干涉條紋的條紋間距就已經不能視為寬度相等，且隨著條紋亮度衰減，對于不同寬度的雙縫片的選取在實驗中顯得更加重要。在成像平面上，激光器發出的相干光的衍射效果可以近似為夫瑯和費衍射，利用近似公式可以得到條紋的光強分布。當相干光線照射在寬度為d雙縫上，根據惠更斯-菲涅耳原理，雙縫上每個間隙都可以視為無數個新的子波源，子波源向各方向發出球面次波，這些次波在成像平面上疊加，可以得到平行于狹縫的條紋圖樣。a為雙縫中每一條縫的寬度，λ為此激光波長。對于是夫瑯和費近似，有成像平面上光強的公式［20］：

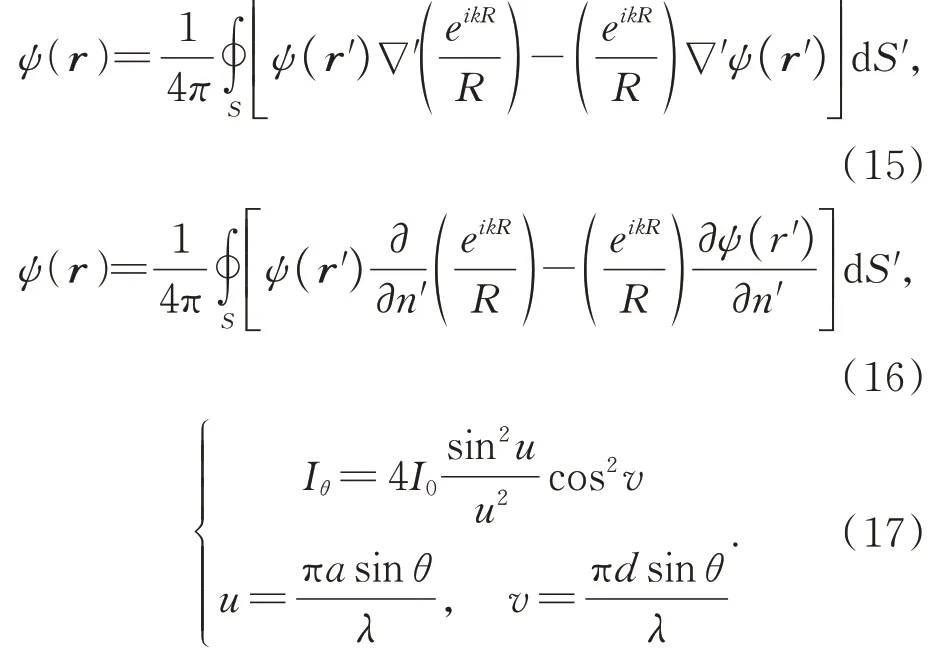
可以看出，紋影系統構型對條紋紋影法測量精度存在影響。根據公式（17），對影響成像平面上光強的變量進行仿真比較。

當波長λ=560 nm 時，對于夫瑯和費單縫衍射的光線強度可以計算得出。取雙縫中心對應成像平面為條紋中心，成像平面距離l+L=800 mm，對成像平面上條紋圖像進行窗口為1的高斯濾波，得到不同狹縫的仿真結果如圖4所示。

假設一束相干光通過（0，0）位置的雙縫經過溫度場，選取兩組成像平面，根據公式（17）可以得到光線穿過折射率場后產生的相應的光程差，如圖5 所示。

根據折射率場存在前后光程差變化，根據激光波長固定的原理，可以求解相位差，通過切面驗證得到條紋偏移量結果如圖6 所示。

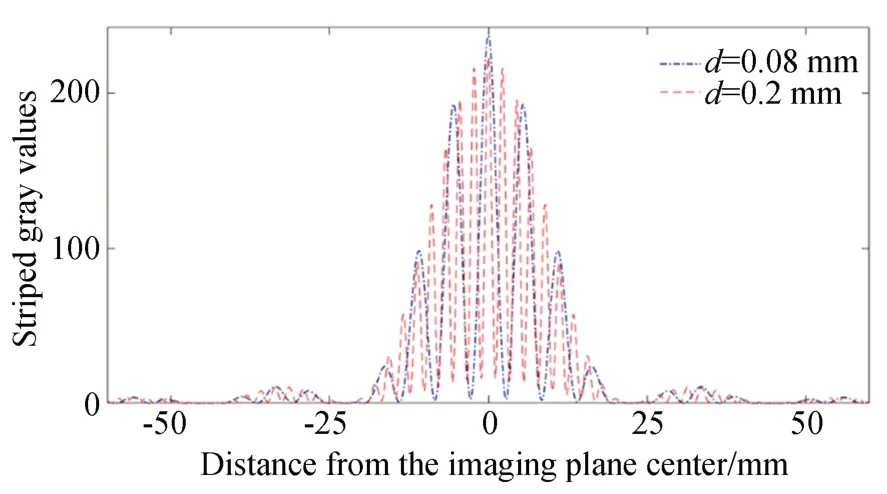
圖4 不同寬度雙縫衍射對應光線強度對比圖Fig.4 Comparison of the light intensity corresponding to different widths of double slit diffraction

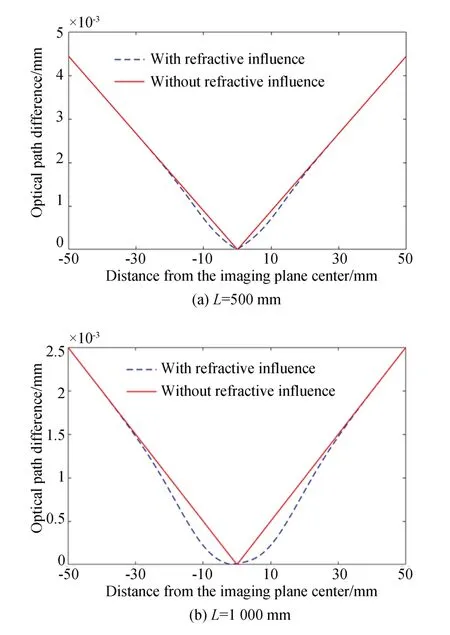
圖5 不同成像平面的干涉條紋光程差Fig.5 Interference fringe optical range difference of different imaging planes

可以看出，調節干涉系統的大小對偏移結果影響成放大倍數關系。當固定雙縫和成像平面的距離，調節火焰在干涉系統中位置時，條紋整體寬度無影響，但隨折射率變化受到很大影響，如圖7 所示，進而可以得到圖8 所示的干涉條紋的偏移量。

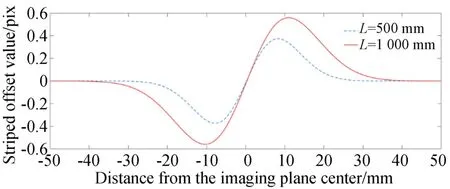
圖6 不同成像平面的干涉條紋偏移量Fig.6 Interference fringe optical range difference of different imaging planes

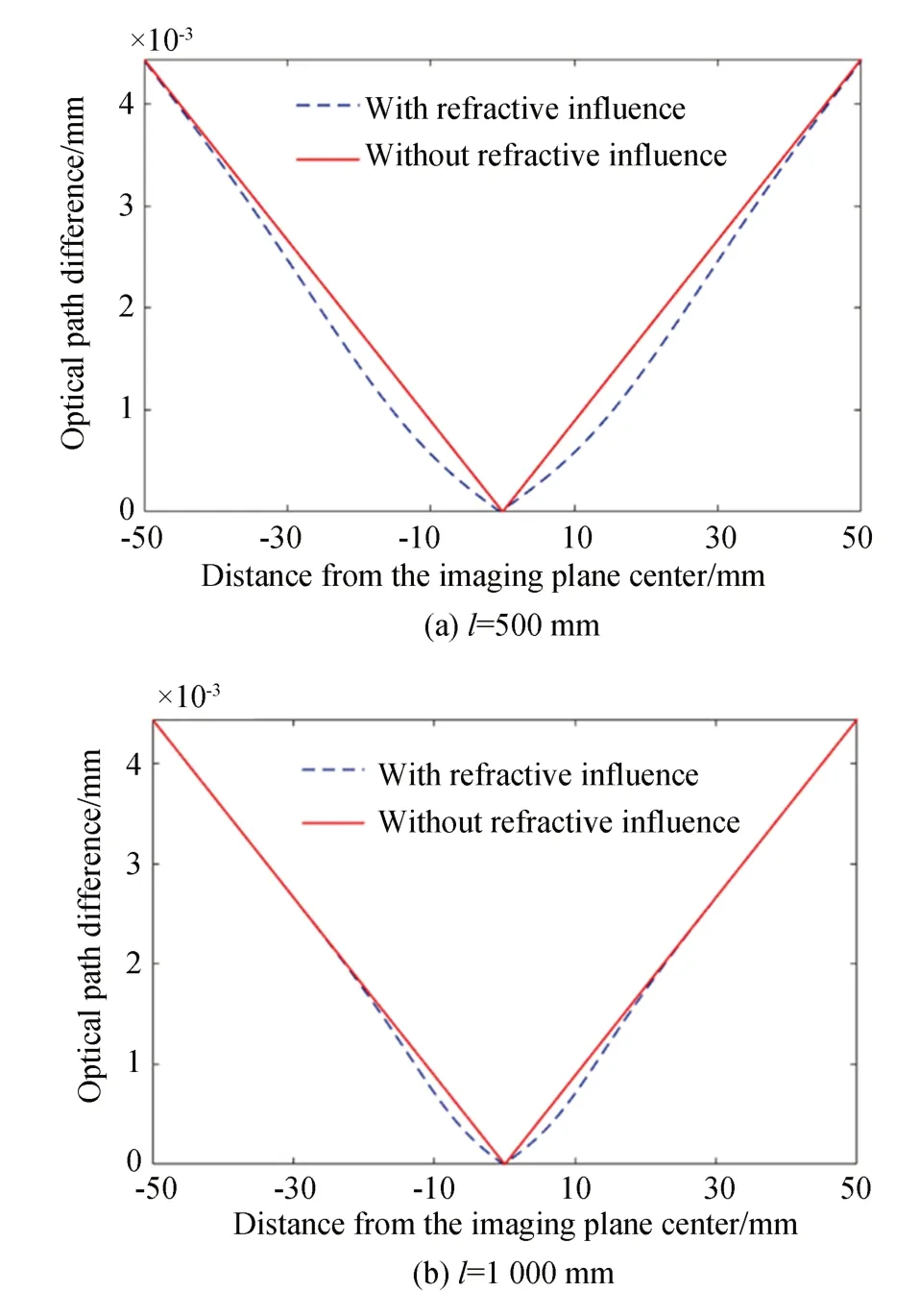
圖7 不同火焰位置的干涉條紋光程差Fig.7 Interference fringe optical path difference of different flame positions

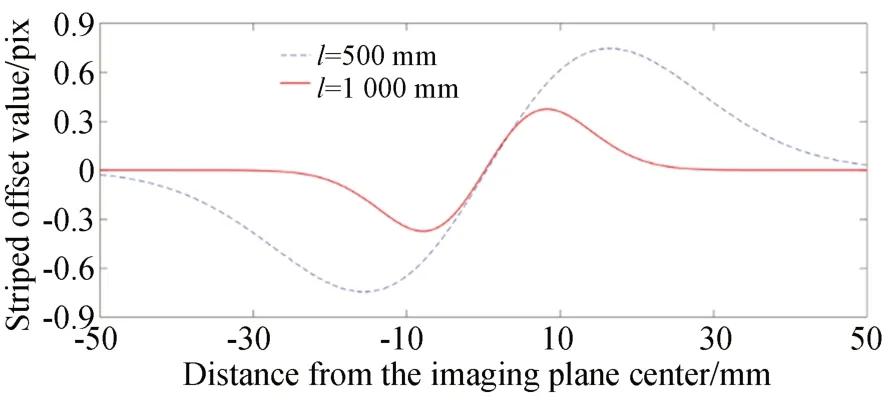
圖8 不同火焰位置的干涉條紋偏移量Fig.8 Interference fringe offsets for different flame positions

當雙縫和成像平面位置固定時，溫度場距離光源越近在成像平面上得到的條紋偏移越明顯。由于光線偏折角的角度很小，因此可以將光線傳播路徑近似為直線。由于激光傳播的性質，光程差就是路徑上折射率的積分。因此可以根據條紋偏移結果解算出火焰溫度分布。

3 干涉條紋紋影測溫的數值模擬

由2.3 節可知，不同的火焰中心溫度對條紋的偏移量存在影響。設定高斯溫度場火焰中心位于（1 000，0）處，雙縫寬度為0.2，成像平面位于y=1 500 處（單位：mm），分別設定兩組軸對稱溫度場，距離中心的溫度如圖9（a）所示，并根據經驗公式求得兩組溫度場對應的折射率分布。

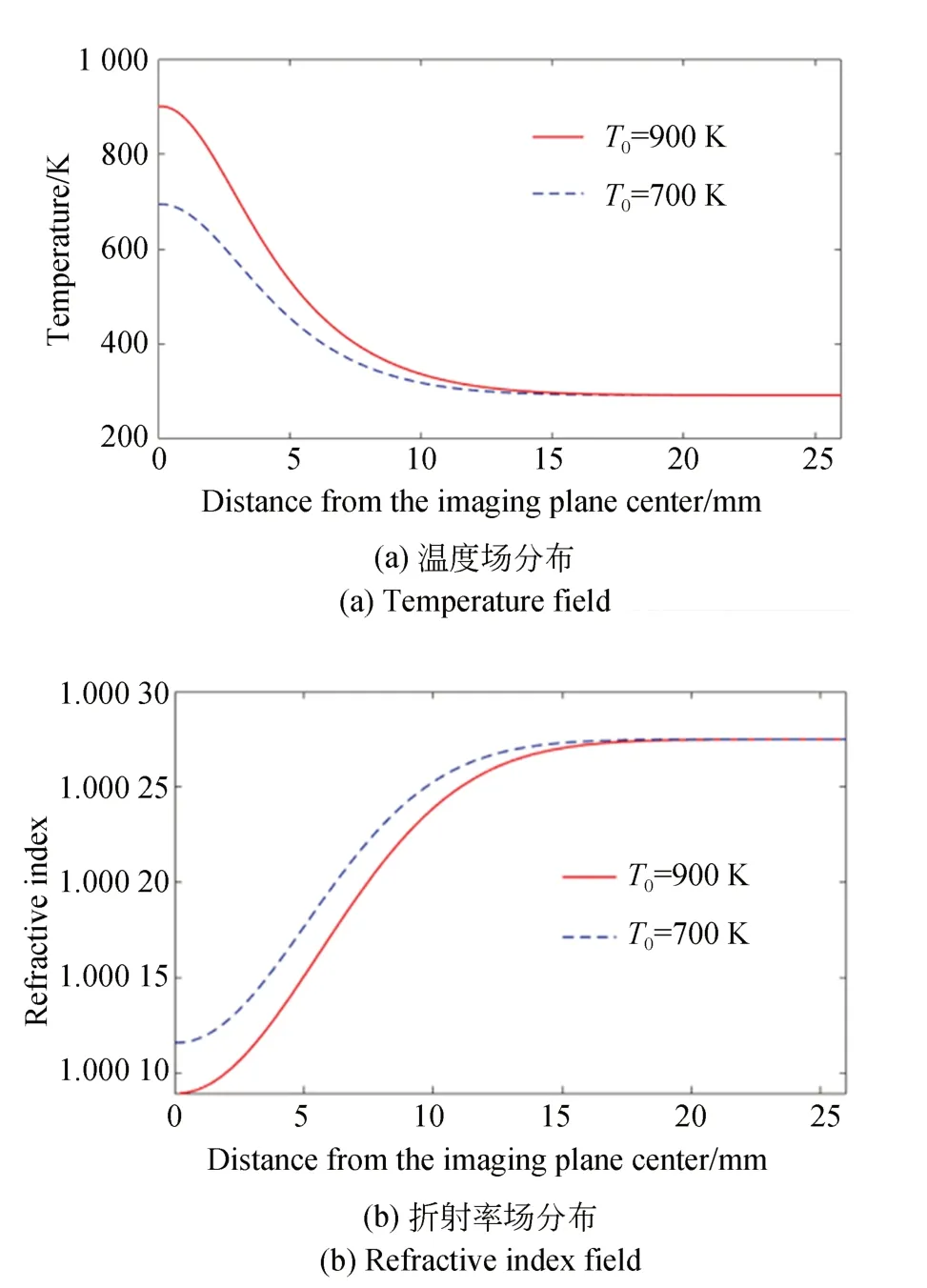
圖9 數值仿真結果Fig.9 Numerical simulation

將折射率分布帶入仿真程序中，可以得到不同中心溫度火焰對應的干涉條紋偏移效果如圖10 所示。可以看出，不同溫度的軸對稱場對應的折射率場不同，進而導致干涉條紋的最大偏移量位置，以及偏移量都不同。

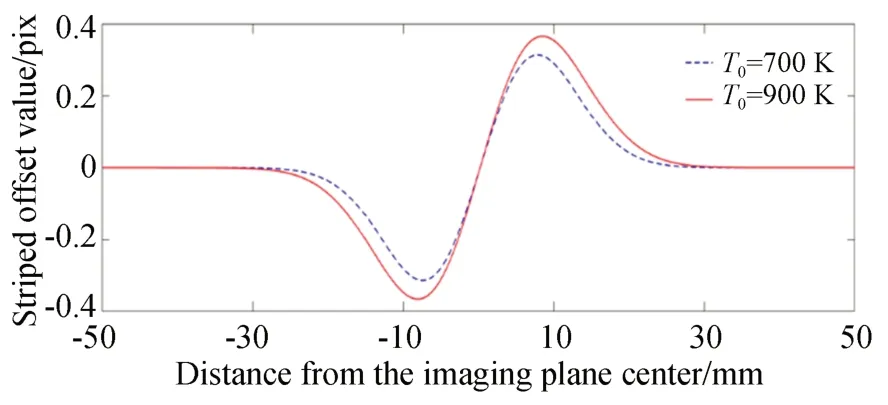
圖10 不同火焰溫度的干涉條紋偏移量Fig.10 Interference fringe offsets for different flame temperatures

可以利用δ（r）采用上述Abel 逆變換，可以反演求得空間中的折射率分布n（r），由于該給定溫度場是標準高斯分布，選取中心角度折射率值進行對比。將中心溫度為800 K 的條紋偏移量帶入公式（6）中，可以計算折射率分布，徑向溫度分布圖如圖所示，由于區域范圍對應實際寬度為20 mm 之內，選取200 組點進行擬合對比，結果如圖11（b）所示。

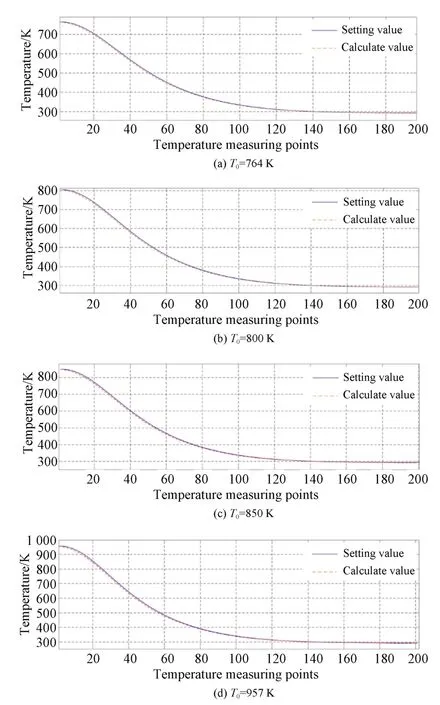
圖11 不同中心溫度下計算結果對比Fig.11 Comparison of calculation results at different center temperatures

分別選取4 種不同的中心溫度，采用仿真方法計算條紋偏移對其產生的影響，并采用Abel 重建獲得溫度分布，如圖11 所示。此處產生最大誤差的原因是投影過程中采用了離散取值并進行的Abel 重建，反演算法時選取了邊緣為可靠已知量，累計中會產生累計誤差，當投影選取的離散間隔足夠小時，誤差可以消除。

通過圖11 的數據對比，已知條紋變化量，可以得知對應溫度分布中心溫度。在這種溫度場變化趨勢固定的情況下，對中心溫度多次求偏移擬合可以得到圖12 所示的最大偏移量與溫度的關系。因此可以根據測量得到的最大偏移量推導出中心溫度。

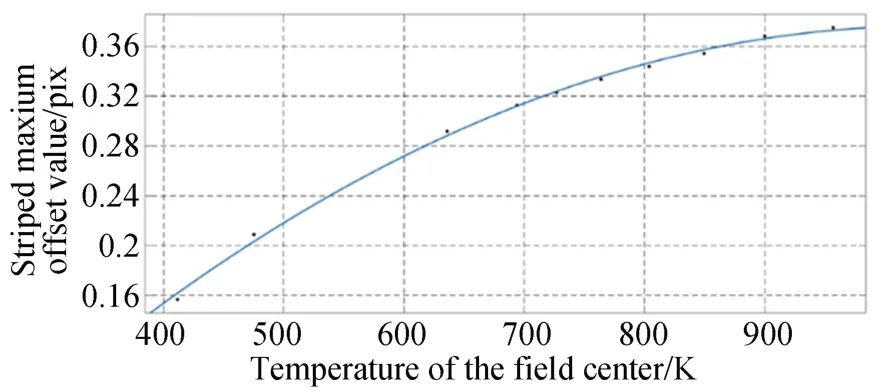
圖12 條紋偏移量最大值隨中心溫度的變化Fig.12 Variation curve of maximum value of stripe deflection with center temperature

4 軸對稱溫度場條紋紋影重建測量實驗

用酒精燈模擬軸對稱溫度場，其中由于火焰燃燒存在的不穩定性，溫度真實結果是采用熱電偶對火焰固定區域進行長時間測量的平均值。在實驗室條件下，采用高精度鉑銥熱電偶（WRP-130S，測量溫度范圍為0～1 600 ℃）配備XMTA-308 型數字溫度顯示器以及高精度三坐標平移臺對酒精燈火焰進行對應坐標的溫度驗證。利用條紋紋影法和背景紋影法同時重建酒精燈的火焰截面，輔以熱電偶測得的實際溫度值。搭建干涉條紋紋影測溫系統如圖13。

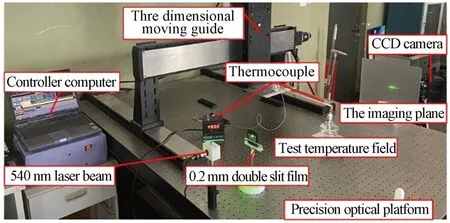
圖13 實驗系統圖Fig.13 Experimental system diagram

在紋影系統之中，由于溫度影響產生的折射率場的存在，激光器在成像平面上得到的干涉條紋會發生抖動，預先標定偏移量對激光頻率造成的影響進行補償。本實驗中使用功率為50 mW的激光模組進行原理驗證。如圖14 所示，先進行小尺度（平面）驗證，當波長為540 nm 激光時，在成像平面上得到的干涉圖樣條紋寬度在3 mm左右。

圖14 干涉條紋圖案Fig.14 Interference stripe pattern

由于50 mW 的激光經過衍射后，中央亮條紋整體亮度較高，得到條紋的光強分布曲線圖15，即干擾偏移量最大值為4 pix，約單個條紋間距的10%。通過激光準直，可以精確地測量固定熱電偶到火焰截面處。相機拍攝的干涉條紋由于明暗特性自身帶有寬度信息。

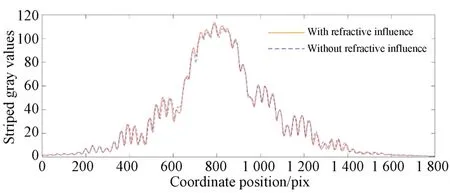
圖15 干涉條紋的灰度分布Fig.15 Grayscale distribution of interfering stripes

通過與無火焰狀態下條紋光強的波形對比，利用相位角和光強成正比的關系，可以求出全部拍攝區域的干涉條紋偏移量如圖16。根據推導的雙縫干涉的光強公式，可以根據條紋的光強衰減變化即可求得相位差。

圖16 干涉條紋的偏移量Fig.16 Offset of interference stripes

根據條紋的偏移量，可以積分得到歸一化折射率的梯度分布，進而得到的重建溫度場如圖17所示。根據條紋寬度，可以確定相可以確定相機拍攝的范圍為20 cm，而由于酒精燈位于狹縫和成像平面中間位置，即重建得到的火焰邊界為10 cm 左右。

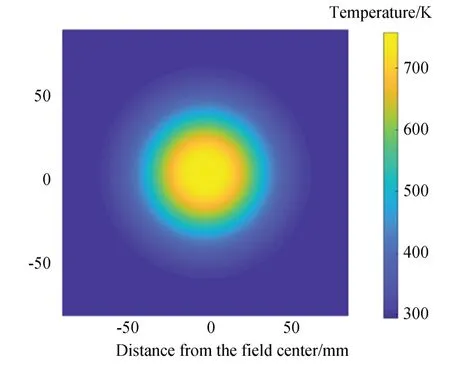
圖17 酒精燈火焰重建溫度場Fig.17 Reconstruction of temperature field by flame of alcohol lamp

采用背景紋影法重建火焰截面與此方法進行比較，如圖18 所示。

實驗將熱電偶固定在高精度平移臺上，每次沿同一方向移動5.00 mm，根據熱電偶測量的酒精燈溫度，和重建得到的溫度場進行對比。結果如圖19 所示。

圖18 背景紋影測量實驗場景圖Fig.18 Background-Oriented Schlieren（BOS）system scene map

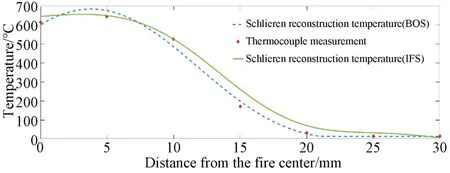
圖19 酒精燈火焰重建結果圖Fig.19 Alcohol lamp flame reconstruction results graph

考慮到熱電偶測溫存在傳熱不均勻的問題，整體重建結果較好。對于酒精燈火焰溫度場的重建，背景紋影法平均誤差為22.7 ℃，對應的測量誤差范圍為0.5 mm；相比條紋紋影法測量范圍可達到0.2 mm，對應平均誤差為15.8 ℃。

5 結論

本文詳細地推導了干涉條紋紋影法軸對稱溫度場測溫的原理，搭建了一個干涉條紋紋影系統，通過對軸對稱溫度場的仿真和實驗，重建出軸對稱火焰的溫度分布。

提出了基于干涉條紋紋影系統的軸對稱溫度測量方法。通過相機拍攝激光干涉得到的偏移條紋信號，進而推斷出待測區域的折射率場分布。利用相機的成像，與傳統激光光譜測溫方法相比，增大了測量區域。通過引入激光干涉，簡化了傳統紋影技術的復雜裝置的同時，保留了紋影技術高分辨率的特點。數值模擬和對比實驗的結果表明，本文提出的方法可以實現軸對稱場的溫度測量。在后續研究中，將進一步研究基于多角度層析重構的非軸對稱溫度場重構方法。