大口徑主鏡的六桿硬點定位機構參數優化

于致遠，吳小霞，王富國

（1.中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033；2.中國科學院大學，北京 100049）

1 引言

望遠鏡是天文觀測的工具，望遠鏡的性能決定了人們可觀測宇宙空間的大小［1-2］。在地基大口徑望遠鏡中，主鏡的定位系統發揮了重要作用，其性能不僅關系到主鏡的位姿保持精度，而且關系到主鏡系統的固有頻率，對望遠鏡的成像質量有重要影響［3-4］。大口徑主鏡定位系統大致可以分為以下三種類型：第一是采用實際定位點對主鏡進行定位，以NTT［5］和VST［6］等望遠鏡為代表，在主鏡的軸向和徑向分別布置若干個定位點，定位點處用各種機構將主鏡和鏡室剛性連接，完全限制主鏡的剛體位移；第二是采用虛擬定位點，以VLT［7］為代表，該方案在主鏡的背部和側面分別布置若干個液壓缸，將背部的液壓缸分成3個相同的扇形區域，將側面的液壓缸分為左右對稱的2個區域，保持每個區域內的液壓缸輸出的壓力相同，如此形成若干個軸向和徑向的虛擬定位點，實現主鏡定位；第三種是采用六桿硬點定位機構進行主鏡定位，使用6 個相同結構的硬點連接主鏡和鏡室，不僅能實現主鏡的定位，而且可以主動調節主鏡的位姿。

六桿硬點定位機構是一種大型并聯機構，在地基大口徑望遠鏡中有廣泛應用，例如LBT［8］、維拉·C·羅賓天文臺望遠鏡（原名LSST）［9］、GMT［10］等。六桿硬點定位機構可以實現主鏡位姿調節，無需軸向和徑向定位的解耦，相比其他定位方案，六桿硬點定位在調節望遠鏡準直方面有明顯優勢，也可以應用于將大口徑反射鏡拼接形成主鏡的方案。六桿硬點定位機構布置在主鏡背部，因此主鏡側面無需布置定位機構，一定程度上簡化了主鏡定位系統的結構。

六桿硬點定位機構有廣泛的發展前景，國內有學者開展了相關研究，胡佳寧等［11］總結了六桿硬點定位機構在國外大口徑望遠鏡中的應用，對其結構特點和主要指標進行了對比和總結。徐宏等［12］研究了LBT，GMT 等望遠鏡使用的六桿硬點定位機構，總結并論述了六桿硬點定位機構的工作原理以及硬點中的位移促動器的結構特點。魏夢琦等［13］分析了六桿硬點定位機構的相關參數指標，對硬點分布半徑、定位夾角、硬點長度等參數分別進行了優化。

為了將六桿硬點定位機構用于4 m 口徑碳化硅主鏡的定位，需要確保主鏡的六桿硬點定位系統有足夠高的固有頻率以滿足設計指標的要求。固有頻率是主鏡定位系統的關鍵技術指標，目前國際上主流的6～8 m 級望遠鏡，無論是采用彎月型薄主鏡還是蜂窩輕量化主鏡，其主鏡系統固有頻率普遍在15 Hz 以上，例如6.5 m 口徑MMT 望遠鏡主鏡系 統固有頻率為20 Hz［14］，8.4 m 口徑的LSST 望遠鏡 為16 Hz［15］，8 m口徑的VLT 和Gemini均達到25 Hz以上［16］。

4 m 口徑碳化硅主鏡屬于背部半封閉式蜂窩輕量化鏡［17］，4 m 望遠鏡要求主鏡系統的固有頻率必須高于15 Hz 才能保證望遠鏡能夠穩定觀測，固有頻率主要受到硬點的軸向剛度、主鏡的質量和慣量、六桿硬點定位機構的構型參數等三個因素的影響，其中硬點的軸向剛度與硬點的結構有關，主鏡的質量和慣量是由4 m 主鏡的力學性質決定的，因此為六桿硬點定位機構選擇合理的空間構型對于提高系統固有頻率有重要意義。

為確保4 m 碳化硅主鏡的六桿硬點定位機構的固有頻率滿足指標要求，對六桿硬點定位機構的構型參數進行了優化設計。首先對六桿硬點定位機構進行了動力學分析，推導了主鏡六桿硬點定位系統的固有頻率方程，建立了六桿硬點定位機構的構型參數、硬點的軸向剛度、主鏡的質量和慣量與主鏡系統的固有頻率之間的函數關系。接著，通過有限元分析獲得了硬點的軸向剛度。然后，基于固有頻率方程，以最大化4 m碳化硅主鏡系統的一階固有頻率為目標，使用遺傳算法對六桿硬點定位機構的構型參數進行優化。最終獲得了構型參數的優化結果。在最優構型參數下，主鏡系統的一階固有頻率明顯高于初始值，優化的效果顯著，能夠滿足望遠鏡對4 m碳化硅主鏡定位系統的固有頻率要求。此外，還對六桿硬點定位機構在最優構型參數時的主鏡系統進行了模態分析，并且校核了主鏡在極限工況下的強度。

2 六桿硬點定位機構的工作原理和數學模型

2.1 六桿硬點定位機構的工作原理

六桿硬點定位機構本質上是一種大型并聯機構，用于調節和保持大口徑主鏡的位姿，廣泛用于地基大口徑望遠鏡的主鏡支撐系統。如圖1所示，六桿硬點定位機構由6 個相同的硬點組成。硬點中設置有位移促動器。硬點的一端在Ai處通過柔性鉸鏈連接到的主鏡背板，另一端在Bi處連接到的鏡室。主鏡、硬點和鏡室組成了一個類似并聯平臺的系統，稱為主鏡六桿硬點定位系統，本文簡稱為主鏡系統。六桿硬點定位機構的原理與六自由度并聯平臺非常相似，調節硬點的長度的即可實現對主鏡相對于鏡室的位姿的調節。當保持所有硬點長度不變時，六桿硬點定位機構完全限制主鏡的空間位移，實現主鏡位姿的保持。

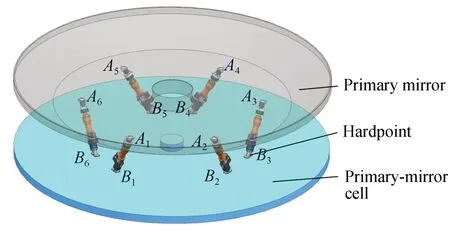
圖1 六桿硬點定位機構的示意圖Fig.1 Schematic diagram of six-hardpoint positioning mechanism

六桿硬點定位機構對主鏡提供位姿調節和定位的功能，不用于提供支撐力，主鏡的重力由多組布置在主鏡背部的氣壓式力促動器承擔，硬點理論上不受力，也不會對主鏡產生力的作用。在望遠鏡工作過程中，由于主鏡位姿改變或者慣性力、風載等因素的影響，硬點可能會出現受力的情況，此時硬點中的力傳感器可以測量出力的大小，然后通過計算機進行解算，計算出所有硬點對主鏡的合力和合力矩，然后通過氣壓促動器產生等效的校正力以抵消上述合力和力矩［18-19］。

2.2 六桿硬點定位機構的運動學模型

運動學模型是動力學建模的基礎，六桿硬點定位機構的結構簡圖如圖2 所示，圖2 是圖1 的簡化，圖2（a）表示六桿硬點定位機構處于初始位姿的狀態，圖2（b）表示進行位姿調節后的狀態。圖中O-xyz是定坐標系，與鏡室固定；O1-x1y1z1是連體坐標系，與主鏡固定；O2-x2y2z2是隨動坐標系，其坐標原點與主鏡中心點重合，各坐標軸方向與O1-x1y1z1的相應坐標軸相同。主鏡作為剛體在空間中有6 個自由度，用包含6 個參數的向量q=［x y z α β γ］T表示主鏡位姿，q可以分解為位置矢量t=［x y z］T和姿態矢量s=［α β γ］T。根據圖3 中的幾何關系可以直接得出六桿硬點定位機構的運動學逆解方程：

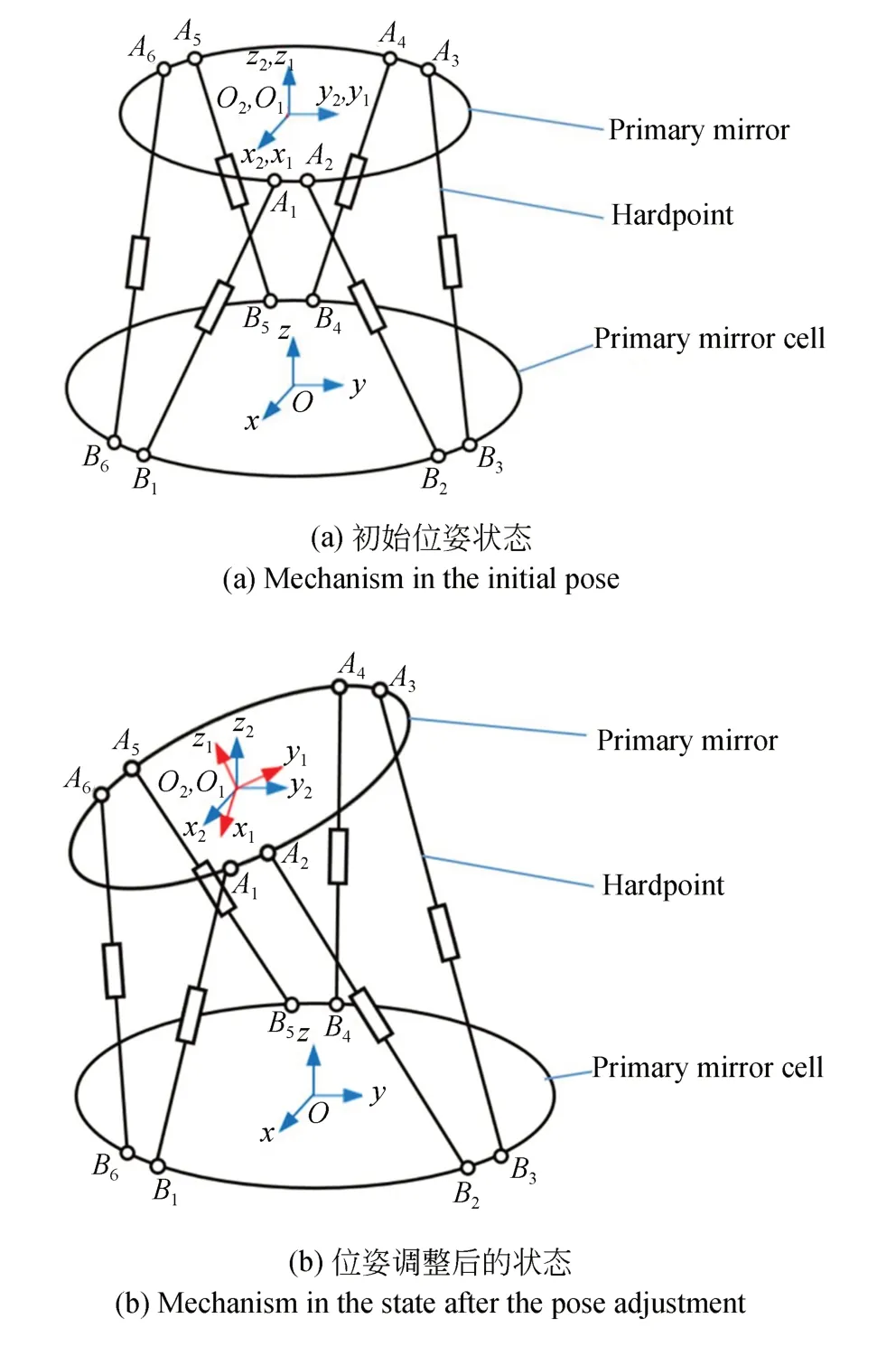
圖2 六桿硬點定位機構的結構簡圖Fig.2 Structural diagram of the six-hardpoint positioning mechanism

其中：i=1，2，…，6，對應6 個硬點；li是硬點矢量，表示硬點的方向，硬點矢量的模是硬點的長度hi；t是主鏡的位置矢量，是坐標原點O1在O-xyz中的坐標；ai是上支撐點Ai在坐標系O1-x1y1z1中的坐標，bi是下支撐點Bi在坐標系O-xyz中的坐標；R是坐標變換矩陣：

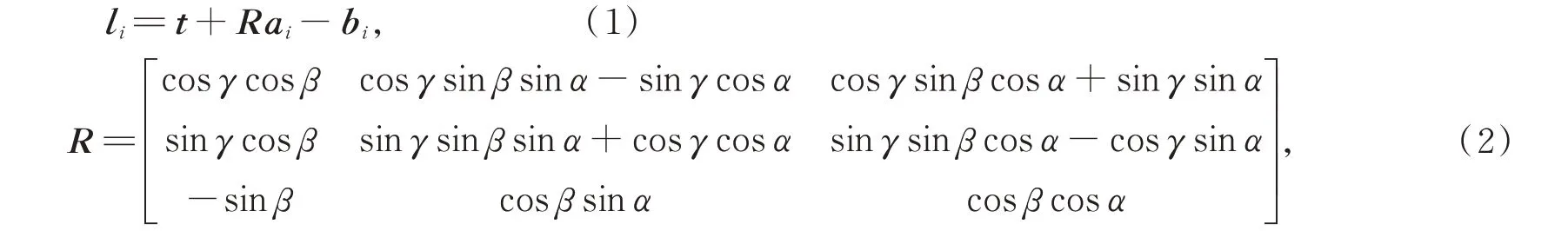
其中：α，β，γ是主鏡繞坐標軸x2，y2，z2的轉角，是姿態矢量s中的元素。在已知六桿硬點定位機構的構型參數的情況下，運動學逆解方程（1）給出了主鏡位姿和硬點長度之間的關系。ai，bi，hi統稱為六桿硬點定位機構的構型參數，通過構型參數可以確定六桿硬點定位機構的空間構型。

根據圖2 中的幾何關系，上支撐點Ai在定坐標系O-xyz中的坐標為：

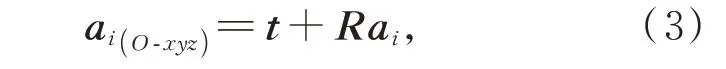
其中：ai（O-xyz）是上支撐點在O-xyz中的坐標。定義主鏡在定坐標系中的速度為q′=［t′，ω］T，ω是主鏡的角速度。對式（3）求導可得上支撐點在定坐標系中的速度vai：

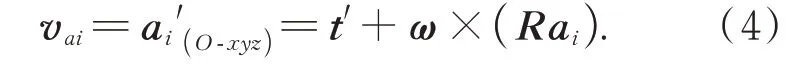
將上支撐點速度vai向硬點方向投影可得硬點的伸長速度li′：

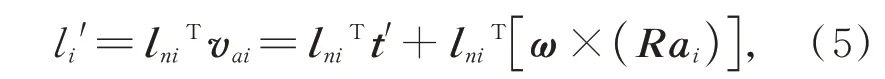
其中：lni是表示硬點方向的單位向量，表達式如式（6）所示：

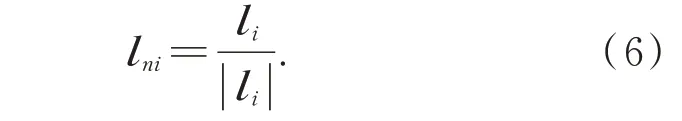
將硬點伸長速度表達式（5）寫成矩陣形式為：

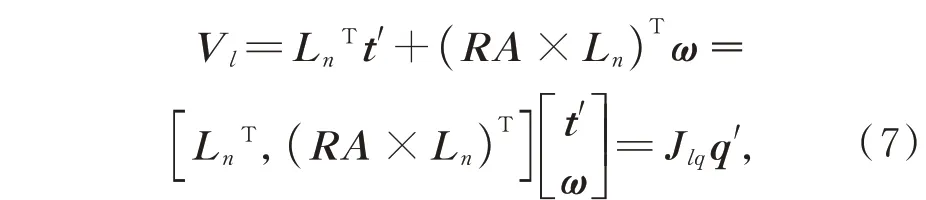
其中：Jlq=［，（RA×Ln）T］是表示主鏡速度和硬點伸長速度關系的雅可比矩陣；硬點伸長速度矩陣Vl、硬點方向矩陣Ln、上支撐點坐標矩陣A的表達式如式（8）～式（10）所示：

2.3 主鏡六桿硬點定位系統的動力學方程

由于硬點的質量遠小于主鏡的質量，因此在動力學分析中忽略硬點質量和慣性力帶來的影響。此外，由于主鏡的剛度遠大于硬點的剛度，因此將主鏡作為剛體分析，只考慮硬點的變形，不考慮主鏡的變形。在這種情況下，主鏡平動的動力學方程為：

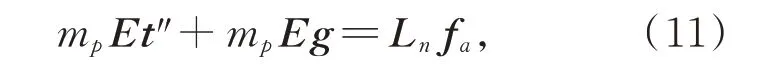
其中：mp是主鏡的質量；g是重力加速度矢量；E為三階單位矩陣；fa是各硬點對主鏡的力組成的向量。主鏡轉動的動力學方程基于歐拉動力學方程：

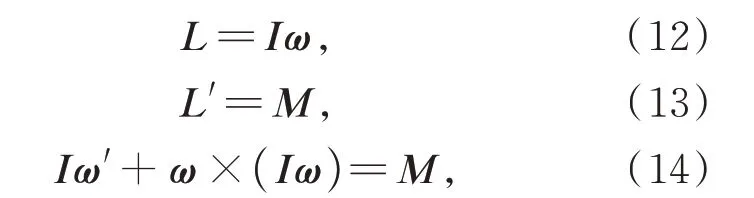
其中：L為研究對象的角動量；I是慣量矩陣；ω是角速度；M是所受的力矩。因此主鏡轉動的動力學方程為：

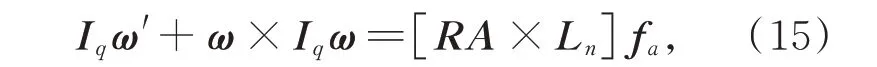
其中：Iq=RIpRT是主鏡在定坐標系中的慣量矩陣；Ip是主鏡在連體坐標系中的慣量矩陣。將主鏡平動動力學方程（11）和轉動動力學方程（15）合并為：

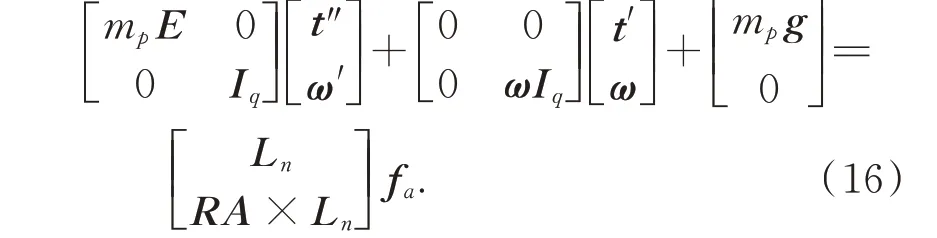
式（16）可以寫成如下形式：

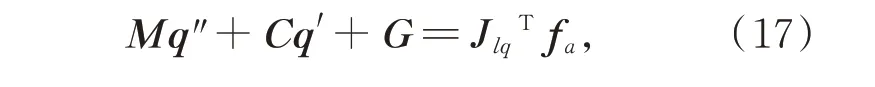
其中：M是主鏡的質量慣量矩陣，C是主鏡的哥氏向心項系數矩陣，G是主鏡的重力矩陣。式（16）和式（17）即為主鏡六桿硬點定位系統的動力學方程。

2.4 主鏡六桿硬點定位系統的固有頻率方程

固有頻率是系統的固有屬性，阻尼和外力對其沒有影響，因此由式（17）得到主鏡系統的振動方程為：

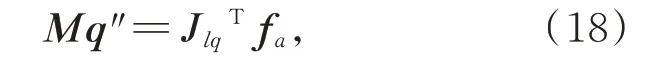
其中，fa是各硬點對主鏡的力組成的向量，表達式為：

其中：K是由各硬點軸向剛度組成的對角矩陣，6個硬點的軸向剛度相同；ΔL是各硬點長度的變化量組成的向量，表達式為：

將式（19）和式（20）帶入振動方程（18），得到主鏡系統的運動微分方程：

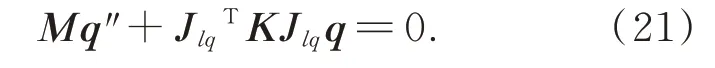
運動微分方程的特征行列式方程為：

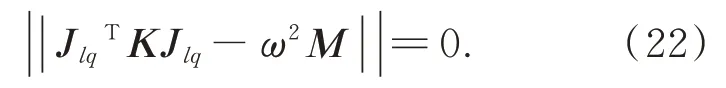
將式（22）稱為主鏡六桿硬點定位系統的固有頻率方程，通過式（22）求解ω即可得到系統的前6 階固有頻率，單位為弧度/秒（rad/s）。可以通過式（23）進行單位換算：

其中，f是固有頻率的另一種形式，單位為Hz。將Jlq和M的表達式帶入主鏡系統的固有頻率方程（22）可得：

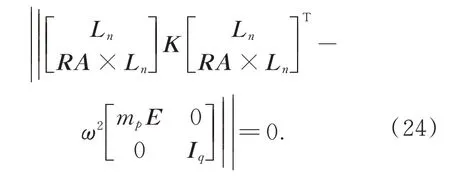
其中：mp是主鏡的質量；Iq是主鏡的慣量矩陣；K是硬點軸向剛度的矩陣；矩陣A中的元素是上支撐點的坐標；根據式（1）、式（6）、式（9），矩陣Ln由六桿硬點機構的構型參數決定。因此，固有頻率方程（22）建立了六桿硬點定位機構的構型參數、硬點的軸向剛度、主鏡的質量和慣量與主鏡系統的固有頻率之間的函數關系，可以求解系統的固有頻率，也說明對于一個特定的主鏡和一組特定結構的硬點，選擇合適的構型參數可以使主鏡系統具有更高的固有頻率。綜上，固有頻率方程（22）可以用于六桿硬點定位機構構型參數的優化設計。

3 硬點軸向剛度計算

針對4 m 口徑碳化硅主鏡設計的硬點的結構如圖3 所示，基于硬點的結構設計，對硬點中的元件分別進行有限元分析，計算他們的剛度，進而得出硬點的軸向剛度。如圖3 所示，硬點中主要包括上柔性鉸鏈、力傳感器、扭矩限制器、分離機構、位移促動器、下柔性鉸鏈等6 個元件，硬點的軸向剛度由這6 個元器件的剛度決定，由于所有元件的均為串聯，因此硬點的剛度可以通過式（25）計算：

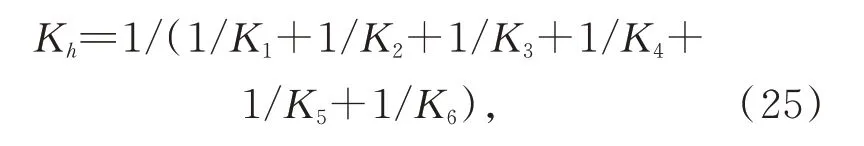
其中：Kh是硬點的軸向剛度；K1～K6分別是硬點中的6 個元件的剛度。

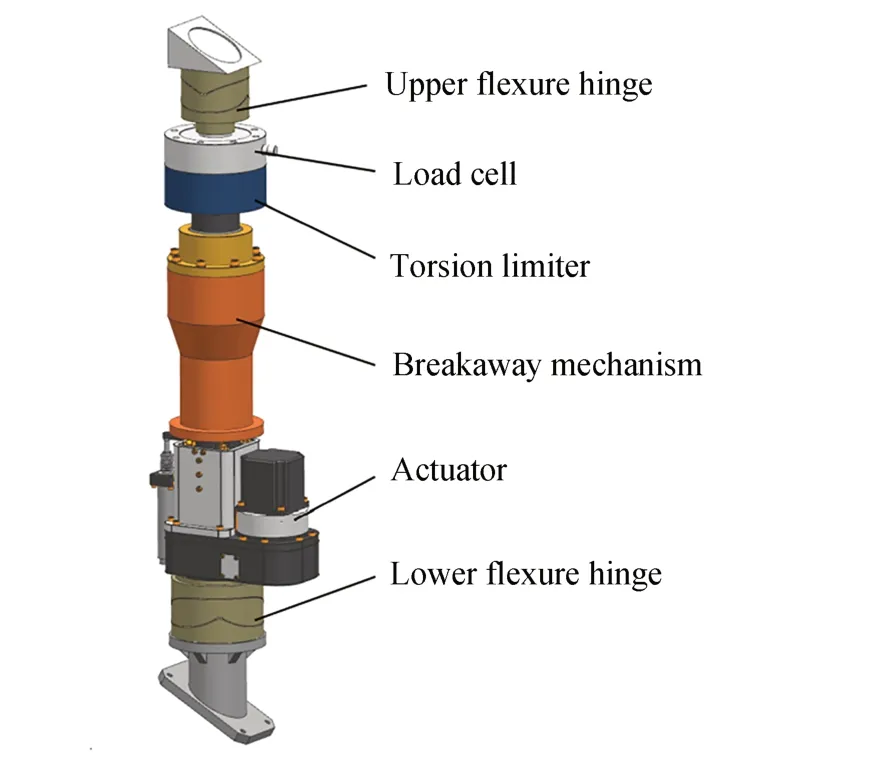
圖3 硬點的結構示意圖Fig.3 Schematic diagram of the hardpoint

在上述元件中，上柔性鉸鏈、扭矩限制器、分離機構、下柔性鉸鏈的結構比較簡單，因此可以通過有限元分析直接計算他們的剛度，向各元件施加1 000 N 的軸向力以及相應的固定約束，得到元件的變形情況，然后通過公式計算他們的剛度：

其中：Ki表示各元件的剛度；F是軸向力的大小；Δxi是通過有限元分析得到的各元件的軸向變形量。各元件的變形云圖如圖4 所示，計算剛度的結果如表1 所示。

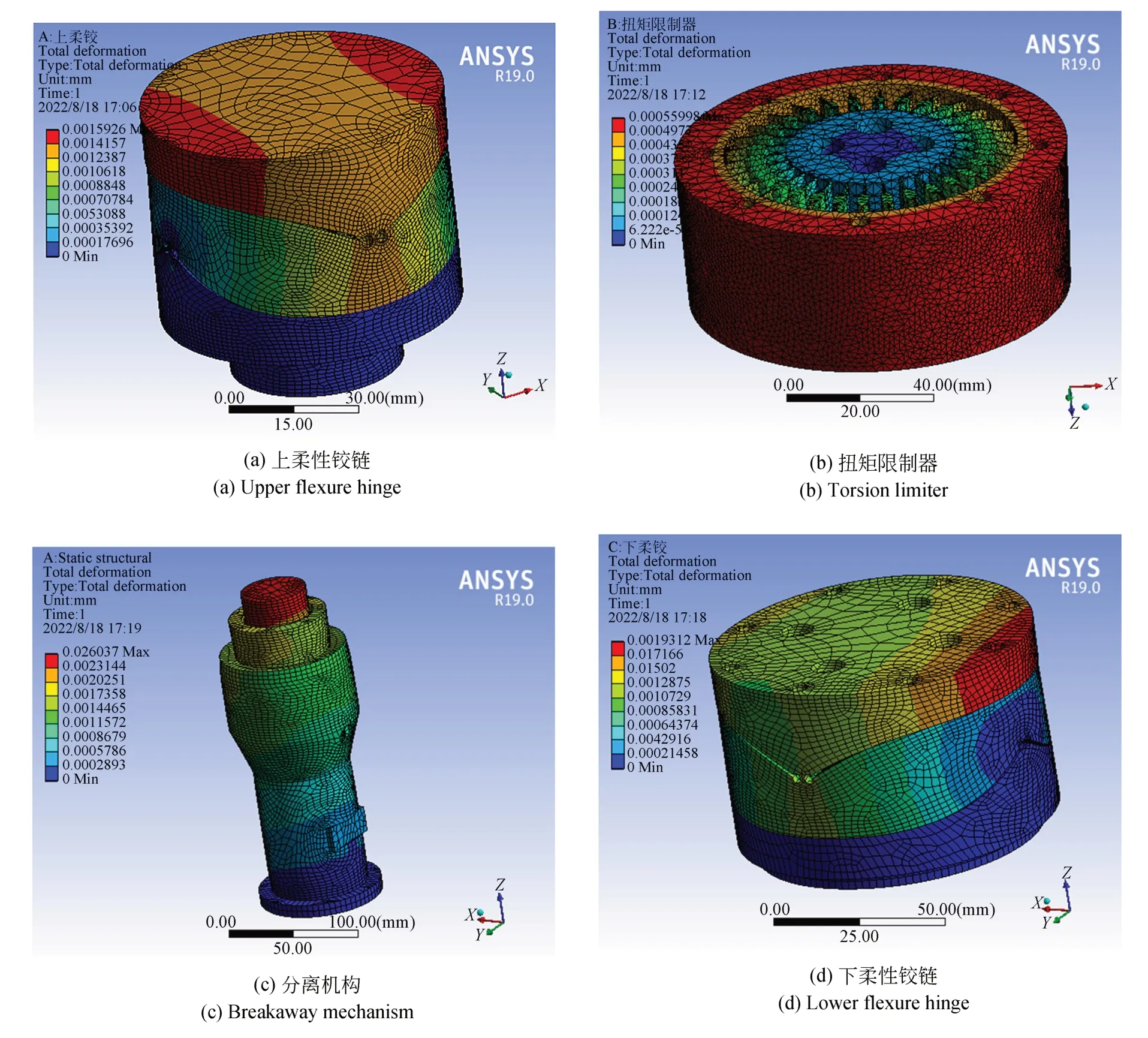
圖4 硬點中部分元件的變形云圖Fig.4 Deformation diagram of some elements in the hardpoint obtained by finite element analysis

表1 硬點中部分元件的軸向剛度的計算結果Tab.1 Calculation results of axial stiffness of some elements in the hardpoint

硬點中的力傳感器使用Interface 品牌的1000 型輪輻式力傳感器，通過查閱產品手冊，得到了力傳感器的軸向剛度為384 N/μm。

硬點中的位移促動器的結構相對復雜，其軸向剛度取決于促動器中的滾柱絲杠、支撐軸承、螺母座、軸套、外殼等多個元器件的剛度，促動器的軸向剛度由以下公式計算：

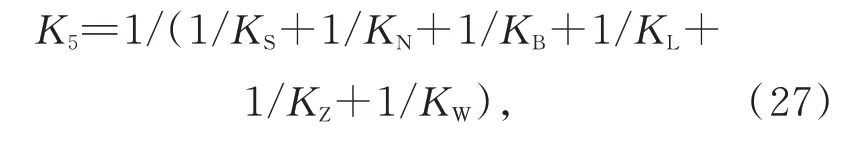
其中：KS和KN分別是滾珠絲杠中絲杠軸和螺母的軸向剛度，可以通過查閱產品手冊獲得，分別為380 N/μm 和73 N/μm；支撐軸承的剛度KB也通過查閱相應產品手冊獲得，剛度值為350 N/μm；KL，KZ，KW分別是螺母座、軸套、外殼的軸向剛度，均通過有限元分析獲得，方法與硬點中的柔性鉸鏈等元件的計算方法大致相同，3 個元件的變形云圖如圖5 所示，得到的軸向剛度分別為4 491.02 N/μm，4 300.46 N/μm，454.71 N/μm。將位移促動器中所有元件的軸向剛度帶入式（27），得到促動器整體的軸向剛度為45.78 N/μm。

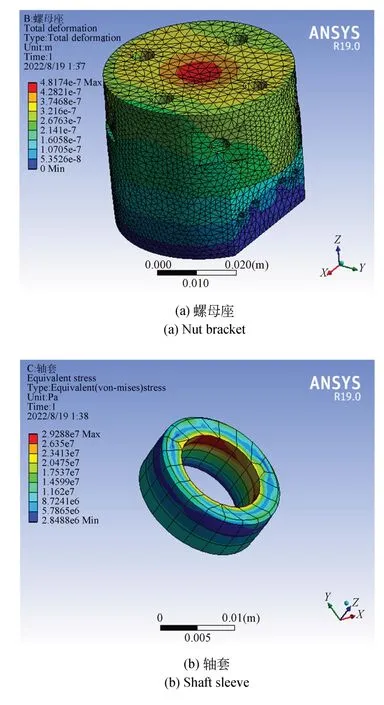
圖5 位移促動器中部分元件的變形云圖Fig.5 Deformation diagram of some elements in the actuator obtained by finite element analysis

最后，將6 個元件的軸向剛度帶入式（25），得到4 m 碳化硅主鏡的硬點的軸向剛度為33.044 N/μm。

4 構型參數的優化設計

基于固有頻率方程（22）、硬點的軸向剛度、4 m 口徑碳化硅主鏡的質量和慣量指標，以最大化主鏡系統的固有頻率為目標，使用遺傳算法對六桿硬點定位機構的構型參數進行優化。

4.1 優化目標

本文的六桿硬點定位機構構型參數優化的目標是最大化主鏡系統的一階固有頻率。一階固有頻率是望遠鏡主鏡系統最關鍵的技術指標之一。為了使望遠鏡能夠穩定觀測，要求望遠鏡有足夠高的基本固有頻率。而為了防止與望遠鏡的振動耦合，要求主鏡系統的固有頻率應高于望遠鏡的基本固有頻率，一般要求至少為該值的兩倍。如果固有頻率低于指標要求，則振動耦合將導致成像質量降低［20］。主鏡系統只有具備足夠高的一階固有頻率，才能避免異常振動，保證望遠鏡觀測穩定。因此，提高主鏡系統的固有頻率對望遠鏡的性能有重要意義。4 m望遠鏡要求主鏡六桿硬點定位系統的固有頻率高于15 Hz。

此外，由于主鏡的質量和轉動慣量已經確定，且硬點的軸向剛度不可能無限提高，因此主鏡系統的固有頻率實際上很大程度上就取決于六桿硬點定位機構的構型參數。雖然六桿硬點定位機構的運動學精度在一定程度上也受到構型參數的影響，但是相比構型參數對固有頻率的影響，構型參數對運動學精度的影響很小。此外，由于硬點中位移促動器的行程較小，因此將靈巧度等指標作為優化目標的意義也不大。綜上，本文最終選擇將最大化固有頻率作為優化目標。

4.2 優化變量及其取值范圍

六桿硬點定位機構屬于并聯機構，其上支撐點Ai和下支撐點Bi的位置分別呈中心對稱分布。用硬點的初始長度l0和支撐點的位置確定機構的構型，支撐點的位置需要4 個參數，如圖6 所示，分別是上支撐點所在的圓的半徑R1、相鄰的上支撐點之間的夾角θ1、下支撐點所在圓的半徑R2、相鄰的下支撐點之間的夾角θ2。通過上述5 個參數可以完全確定六桿硬點定位機構的空間構型。2.2 節中提到將ai，bi以及硬點的長度統稱為構型參數，由于ai和bi可以通過R1，θ1，R2，θ2求解，因此兩種表示方法的意義是相同的。硬點初始長度的設計值為800 mm，無需優化，因此構型參數優化的優化變量為R1，θ1，R2，θ2。

優化變量的取值范圍是根據結構的容許量確定的，首先注意R1和θ1，上支撐點Ai分布在主鏡背板，4 m 碳化硅主鏡屬于背部半封閉式輕量化鏡，背部有徑向筋板和環向筋板，主鏡背部的結構如圖7 所示，為了保證主鏡內部應力的合理分布，也考慮到結構的合理性，因此上支撐點Ai只能布置在徑向筋板和環向筋板的交點，因此R1和θ1的取值范圍如表2 所示。R2和θ2的取值范圍主要考慮鏡室的尺寸，初步設定R2的取值范圍為350～2 000 mm，θ2的取值范圍是0°～120°。此外，為了避免相鄰硬點在空間尺寸上發生干涉，要求相鄰的支撐點不能過于接近，因此將θ2的取值范圍修正為10°～110°，同理，θ1的取值范圍中的“0°”和“120°”應予剔除。

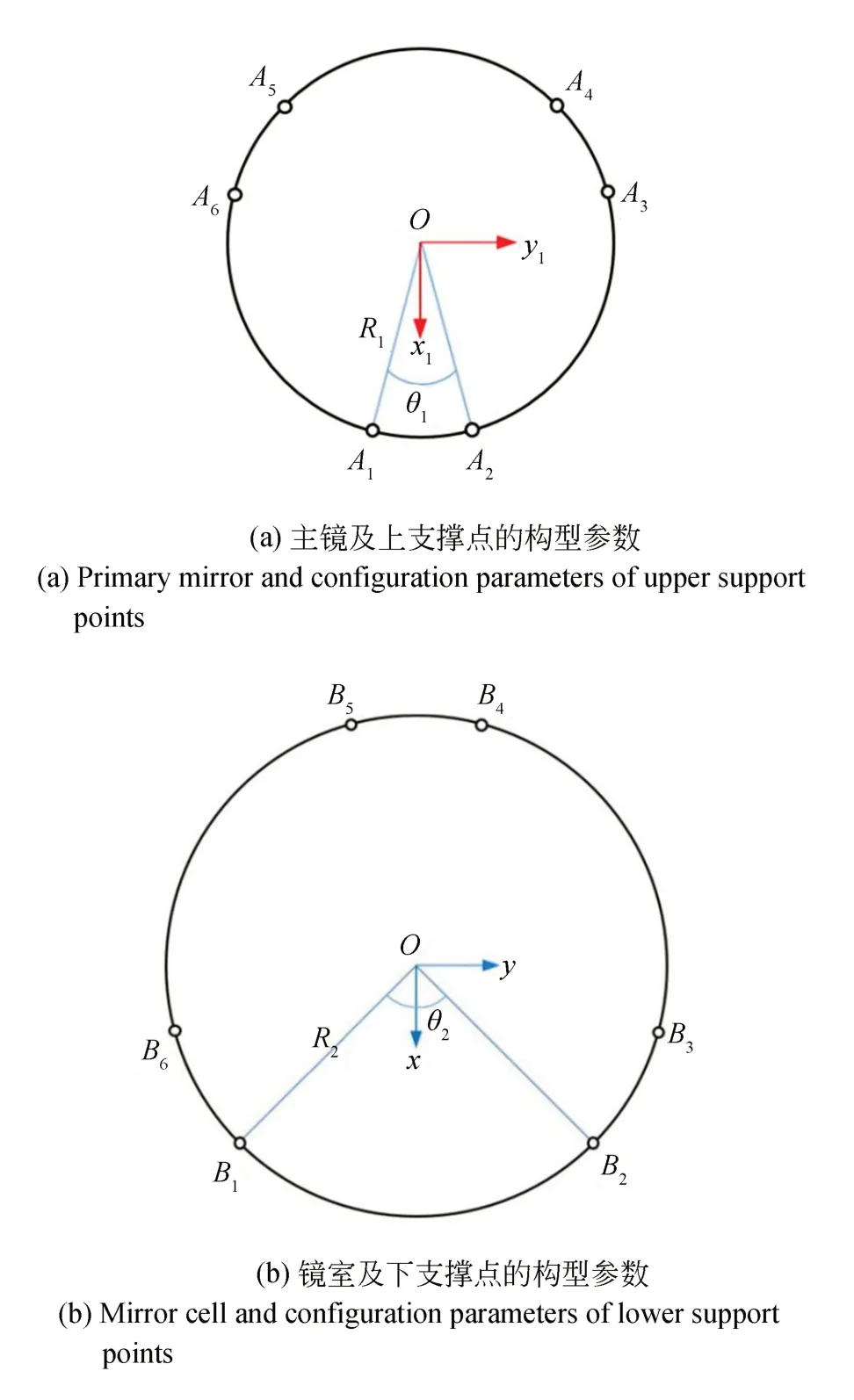
圖6 六桿硬點定位機構的構型參數示意圖Fig.6 Configuration parameters of six-hardpoint positioning mechanism

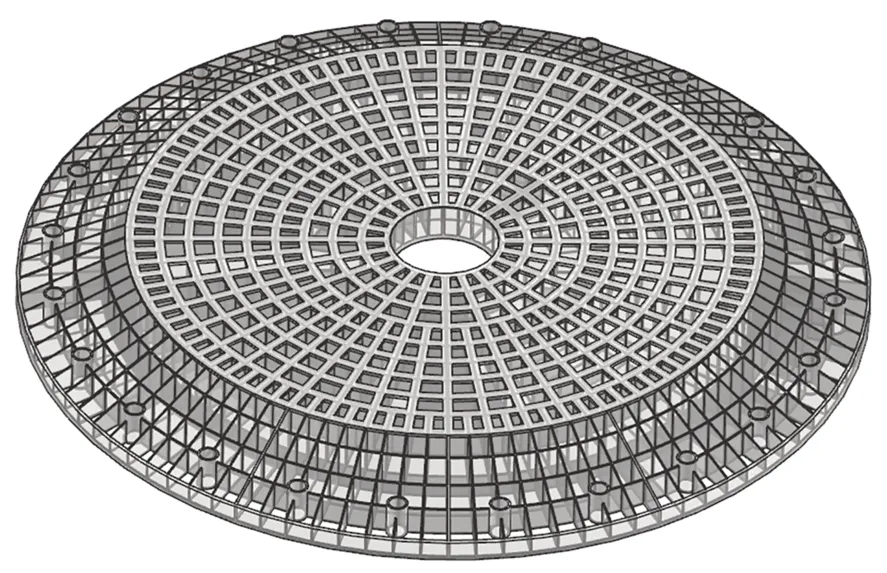
圖7 4 m 碳化硅主鏡的背部結構Fig.7 Backing plate of the 4 m SiC primary mirror

此外，上支撐點Ai和下支撐點Bi之間的距離在水平方向上的投影不能超過硬點的初始長度l0，因此優化變量還必須滿足如式（28）所示的關系：

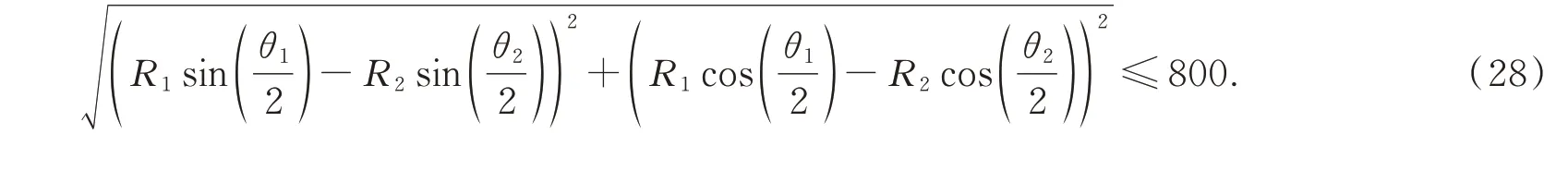
表2 上支撐點分布圓半徑R1和上支撐點之間的夾角θ1的取值范圍Tab.2 Value ranges of the radius R1 of the upper support point distribution circle and the angle θ1 between the upper support points

4.3 構型參數優化的方法

綜上所述，本文的構型參數優化問題可表示為：

本文采用遺傳算法進行構型參數優化，該算法提出于上世紀70 年代，是通過模擬生物自然進化過程搜索最優解的優化算法，其主要特點是有較好的全局搜索能力、可以自適應地調整搜索方向［21-22］。設定優化目標為最大化主鏡系統的一階固有頻率，設定優化變量R1，θ1，R2，θ2及其取值范圍。在優化中將硬點的軸向剛度按照第3 節有限元分析的結果設定為33.044 N/μm。此外，4 m碳化硅主鏡的質量為1 684.4 kg，碳化硅材料的主要力學參數包括：密度3 050 kg/m3，楊氏模量3.92×1011Pa，泊松比0.25，將以上參數也帶入優化算法。

5 結果與討論

5.1 構型參數優化的結果

構型參數優化結果如表3 所示。通過遺傳算法優化后，構型參數R1，θ1，R2，θ2的值分別為1 484 mm，30°，1 670 mm 和76°，4 m 碳化硅主鏡系統在該構型參數下的一階固有頻率為30.83 Hz，能夠滿足4 m 望遠鏡對主鏡系統的固有頻率大于15 Hz 的要求。在遺傳算法中設定的初始種群的個體數量為80，每次迭代樣本數40，最大迭代次數14 次，最終產生了395 組數據。

表3 中同時列出了主鏡系統在初始構型參數下的一階固有頻率，初始構型參數是根據經驗初步分析選定的一組較優的參數，初始構型參數下主鏡系統的一階固有頻率是14.69 Hz。將其與遺傳算法得到的結果進行對比可知，在遺傳算法得到的構型參數下，主鏡系統的一階固有頻率相對初始參數提高了109.9%。將遺傳算法得到的構型參數作為優化的最終結果，即R1，θ1，R2，θ2的最優值分別為1 484 mm，30°，1 670 mm 和76°。

表3 六桿硬點定位機構的構型參數的優化結果Tab.3 Optimization results of configuration parameters of six-hardpoint positioning mechanism

5.2 最優構型參數下的4 m 碳化硅主鏡系統的固有頻率計算和模態分析

分別用固有頻率方程和有限元分析的方法計算4 m 碳化硅主鏡系統的固有頻率，對兩種方法得到的結果進行對比和分析。

首先使用固有頻率方程（22）計算主鏡系統的固有頻率，所有物理量均使用國際單位。根據最優構型參數和2.2 節的內容計算R，A和Ln，進而得到Jlq。然后基于硬點的軸向剛度值33.044 N/μm 得到矩陣K=diag（3.304 4×107，…，3.304 4×107）。4 m 碳化硅主鏡的質量是1 684.4 kg，主鏡的慣量矩陣Iq為：

進而得到主鏡的質量慣量矩陣M=diag（1 684.4，1 684.4，1 684.4，1 659.4，1 659.4，3 283.2）。將上述物理量帶入固有頻率方程（22）并求解，使用式（23）進行單位換算，得到主鏡系統的前6 階固有頻率的計算結果如表4 所示。由于方程（22）沒有考慮主鏡的變形，因此更高階的固有頻率無法用方程（22）求解。

然后，基于最優構型參數建立主鏡和六桿硬點定位機構的模型，將硬點簡化為桿件并設定軸向剛度為33.044 N/μm，導入有限元軟件進行模態分析，得到主鏡系統的前10 階固有頻率，如表4 所示。此外，還得到了系統的前10 階模態振型，如圖8 所示，圖8（a）～圖8（j）分別為主鏡系統在最優構型參數下的1～10 階振型，其中1～6 階表現為主鏡的剛體位移：1，2 階為主鏡的橫向平移；3 階為主鏡沿光軸方向的平移；4，5 階為主鏡橫向翻轉；6 階為主鏡繞光軸方向的旋轉，6 階以上的振型則表現為主鏡本身的變形。有限元分析的結果基本驗證了前文的觀點，即主鏡系統的前6 階振型體現為主鏡的剛體位移，而更高階振型體現為主鏡的變形。

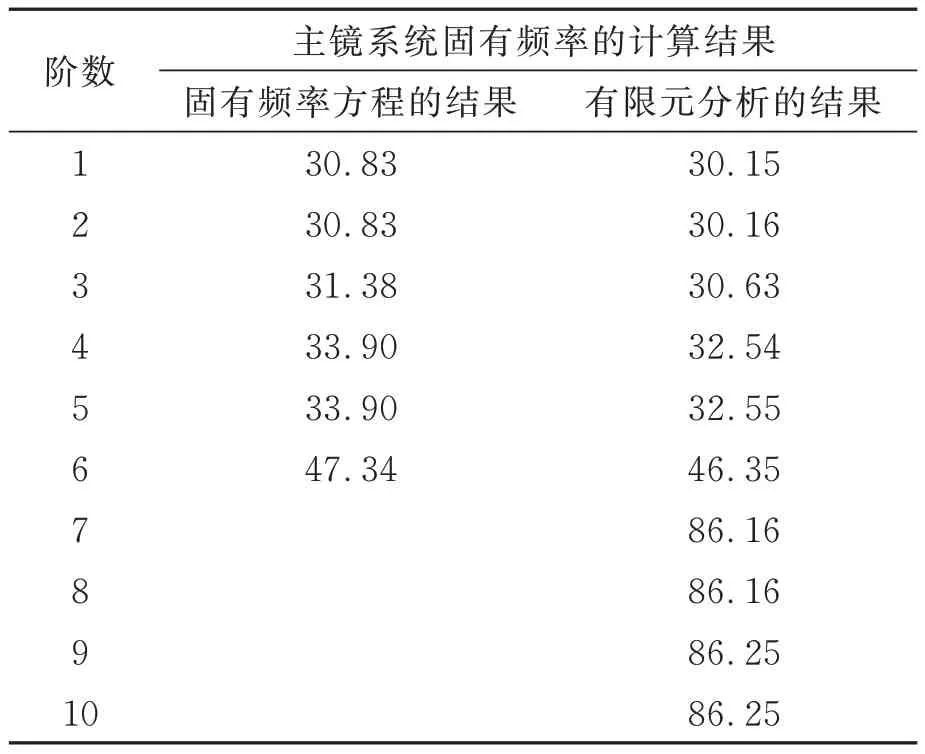
表4 主鏡系統在最優構型參數下的固有頻率Tab.4 Natural frequency of the primary mirror system under optimal configuration parameters （Hz）

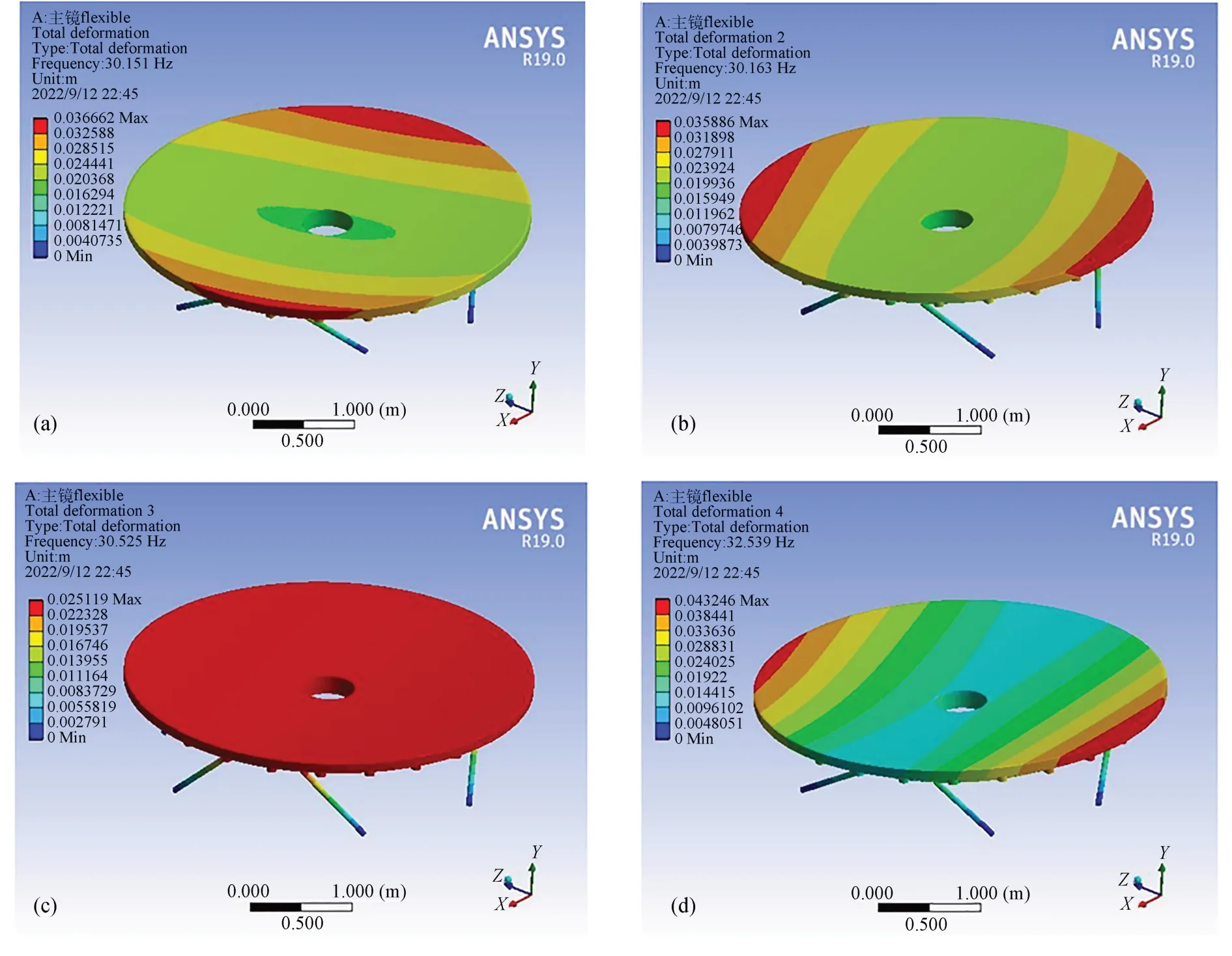
圖8 4 m 碳化硅主鏡的六桿硬點定位系統在最優構型參數下的1～10 階模態振型Fig.8 First to tenth order modes of the six-hardpoint positioning system of 4 m SiC primary mirror under the optimal configuration parameters

結果表明，使用有限元計算的固有頻率和通過固有頻率方程計算的固有頻率非常接近，說明本文推導的固有頻率方程是正確的。然而表4 的結果說明，通過固有頻率方程計算的結果與有限元分析的結果存在一定的誤差，一方面是因為有限元分析本身存在一定的誤差，另一方面是因為本文的固有頻率方程沒有考慮主鏡的變形和硬點的質量，兩個因素的共同作用導致了計算結果的誤差，整體上看，誤差的大小在可接受的范圍內。

5.3 最優構型參數下主鏡的強度校核

為了檢驗六桿硬點定位機構按最優構型參數排布時的主鏡安全性，通過有限元分析計算了極限工況下的主鏡內部應力，判斷主鏡是否安全。考慮到發生斷電、地震等意外情況時主鏡可能會因為受力過大而導致的損壞，六桿硬點定位機構中設置有安全裝置，即在每個硬點中的分離裝置，一旦其受力達到閾值，則可以快速降低剛度并提供一定的伸長或縮短，使得主鏡落于安全防護組件上，從而保護了主鏡。當硬點機構受力閾值設置為1 000 N 時，即每個硬點上施加1 000 N 的軸向力，有限元分析的結果如圖9 所示，主鏡中第一主應力的最大值出現在硬點與主鏡的接觸點處，第一主應力的最大值為0.87 MPa，該值遠小于碳化硅材料100 MPa 的抗彎強度［23］。有限元分析的結果說明，六桿硬點定位機構按照本文的最優構型參數排布時，主鏡在極限工況下可以保證安全。

6 結論

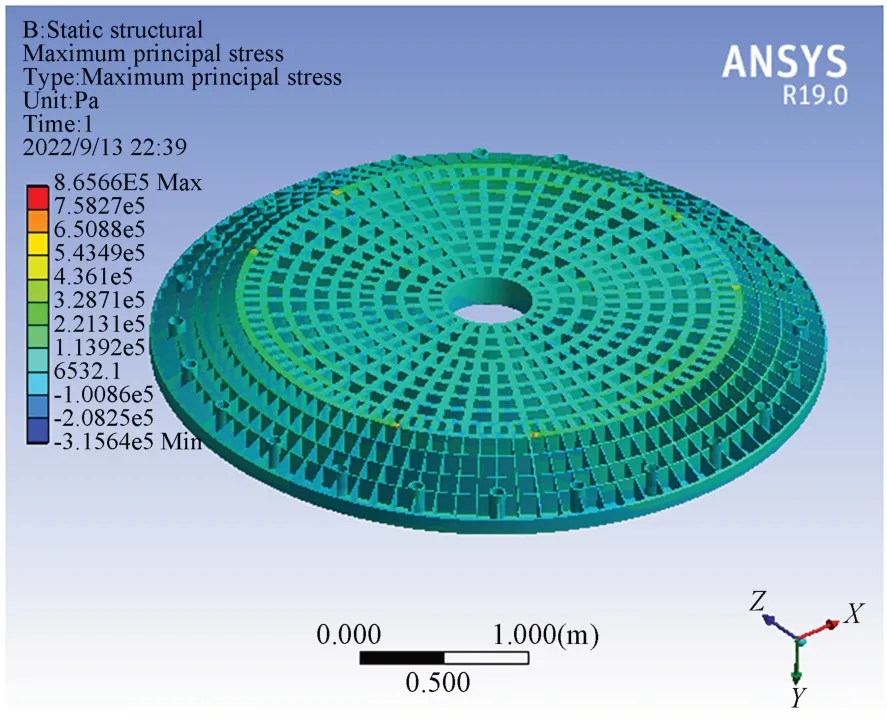
圖9 主鏡在極限工況下的最大主應力云圖Fig.9 Maximum principal stress diagram of the primary mirror under extreme working condition

為了提高4 m 口徑碳化硅主鏡的六桿硬點定位系統的一階固有頻率，對六桿硬點定位機構的構型參數進行優化設計，獲得了最優構型參數。首先推導了主鏡系統的固有頻率方程，建立了六桿硬點定位機構的構型參數與主鏡系統的固有頻率之間的函數關系。接著通過有限元分析獲得了4m 碳化硅主鏡的硬點的軸向剛度。然后基于固有頻率方程，使用遺傳算法對六桿硬點定位機構的構型參數進行優化。此外，還對最優構型下的4m 碳化硅主鏡系統進行了模態分析。優化結果表明，構型參數R1，θ1，R2，θ2的最優值分別為436 mm，30°，600 mm 和109°，在最優構型參數下，主鏡系統的固有頻率達到30.83 Hz，相對初始值有較大提高，能夠滿足4 m 望遠鏡對主鏡系統的固有頻率大于15 Hz 的要求。本文的研究為4 m 碳化硅主鏡的六桿硬點定位機構提供了最優構型參數，使主鏡系統能夠滿足固有頻率指標的要求，對保證望遠鏡的穩定觀測有重要意義。此外，本文的構型參數優化方法可以應用于與各種口徑的主鏡配套的六桿硬點定位機構，為六桿硬點定位機構的參數優化提供了可行的方法。