培養初中生數學問題解決能力的課堂教學實施策略
文/高州市教師發展中心 陳 瓊
問題解決是數學教學的中心環節,其目的不是單純的盡量多和盡量好的解決問題,而應該是以培養問題解決的能力為目的。正如貝格所說:“教授數學的真正理由是因為數學是應用極廣的科學,且特別地教授數學還有利于解決各種各樣的問題.學習怎樣解決問題是學習數學的真正目的。”現在的數學教學不僅是要教學生掌握知識,更重要的是要有由“掌握知識技能為核心”的教學轉向“發展思維訓練為核心”的教學,形成系統的知識判斷能力、高階思維解決問題能力。
一、把上課的重心轉移到預設引領下的生長教學
1.創設切近真實又開放的問題情境
情境化的教學,本質上就是在脫離數學,從實際問題到數學問題的數學抽象的過程,也就是核心素養的抽象能力。開放的情景就是我們利用這個情境素材從不同的維度展開。下面以北師大版數學九年級下冊《銳角三角函數》為課例,素材由梯子的傾斜程度問題引入正切的概念,教學時呈現多種形情形;高度相同,底邊不同;底邊相同,高度不同,等等,讓學生討論,這是一個很好的開放性的問題,學生的回答可能多種多樣,比如有的學生可能會想到度量角度,還有的學生可能會想到AC等于ED,因此比較BC和FD的長短,就可判斷梯子的傾斜長度。角的改變引起陡的程度的變化,而同樣是梯子下滑的素材,但是在2020年的中考題里面,
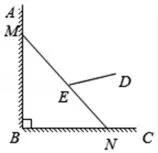
【考題】有一架豎直靠在直角墻面的梯子正在下滑,一只貓緊緊盯住位于梯子正中間的老鼠,等待與老鼠距離最小時撲捉.把墻面、梯子、貓和老鼠都理想化為同一平面內的線或點,模型如圖,∠ABC=90°,點M,N分別在墻面BA,BC上,梯子MN的長度始終保持不變,MN=6,老鼠E在MN的中點處,貓在D點處,它到墻面BA,BC的距離分別為4和3.在此滑動過程中,貓與老鼠的距離DE的最小值為 .
這個問題觀察的重心,跟本節課思考的維度不同,其觀察的不是角,而是斜邊中線在運動過程中的軌跡問題。
2.預設驅動思考又發散的問題情境
初中數學課堂教學,十多年前在基礎知識、基本技能方面落實得比較到位。但缺少了培養學生的數學思維以及四能“發現問題、提出問題、分析問題、解決問題”方面的教學。也就是要用問題引導學生去發現問題、提出問題,同時情境有一定的障礙性,需要一定的邏輯分析能力,要臨界于學生的最近發展區,使學生進入“心求通而未得,口欲言而未能”的理想狀態.例如:九年級上冊《反比例函數的應用》這節課,通過問題設計,引導學生能夠運用函數的思維方式去觀察、分析現實社會中問題,能用反比例函數解決簡單實際問題,
【問題】某蓄水池的排水管每時排水8m3,6h可將滿池水全部排空。
(1)蓄水池的容積是____?
(2)如果增加排水管,使每時的排水量達到Q(m3),那么將滿池水排空所需的時間t(h)將如何變化?
(3)寫出t與Q之間的關系;
(4)如果準備在5h內將滿池水排空,那么每時的排水量至少為____?
(5)已知排水管的最大排水量為每時12m3,那么最少____時間可將滿池水全部排空?
二、在課堂教學中發展深度學習,培養學生的思維能力
培養學生的思維能力,應該從提高學生的思維品質入手,培養學生思維的深刻性,教育學生學會透過現象看本質,學會全面地思考問題,養成追根究底的習慣。如:我在講評一道《關于線段、射線、直線概念的理解和運用》的題目“……數軸上表示不小于,且不大于3的點組成的是什么圖形?……”孩子們對此不難理解,很快根據定義得出答案:線段!我看到孩子們情緒高漲,拋出一個問題讓他們討論,“數軸上表示大于,且小于3的點組成了什么圖形?”。首先題目提出的數軸上的點組成的圖形而這圖形只能有三種:線段、射線、直線,學生們又從定義和端點個數等多方面展開思考.通過討論讓孩子們加深對相關概念的理解和提高獨立思考、分析問題的能力.在教學過程中,一方面要盡量使學生掌握數學概念、原理的本質,提高所掌握的數學知識的抽象程度,因為所掌握的知識越本質、抽象程度越高,其適應的范圍就越廣泛,思維的靈活性也就越高.在教學中要鼓勵學生提出不同的意見,使學生體驗到創新思維的樂趣,同時引導學生反思和剖析自身的思維過程,了解自已在學習中運用了哪些基本的思考方法、技能和技巧?它們的合理性如何?效果如何?有沒有更好的方法?學習中走過哪些彎路?犯過哪些錯誤?原因何在?等等.
三、在課堂教學中倡導研究性學習
研究性學習是一種能適應新形勢的需要,是培養創新意識和激發創造動機的新興教學理念。研究性學習進入課堂,是培養學生養成“研究型”認知學習方式的一種有效路徑,在研究性學習中以學生為主體,知識的獲取途徑來自于自身的研究活動,在研究過程中發展學生的分析能力、推理能力、決策能力以及問題解決的能力等。
在課堂上,研究性學習能讓學生通過自身的潛能、自主地去獲取知識,這種教學模式有助于學生將自已各項技能和各種能力得到最大化的發展,數學問題解決能力得到極大提高。例如,在探索直線平行條件一課中,如何得出“同位角相等,兩直線平行”的判定定理時,讓學生通過實踐“扮演裝修工角色”向墻上釘木條,如何使木條a平行木條b,教師從中引導,讓學生怎樣把實際問題轉化為數學問題來,從而得出木條a平行木條b的必要條件是什么?使學生初步感知“同位角”和“同位角相等,兩直線平行”的判定定理。接著再引導學生動手操作“借助三角尺畫平行線”這一過程,最后學生通過自主探索研究,討論分析、推理得出結論。
以上是從數學問題解決能力的角度,闡述了在初中數學教學中培養學生問題解決能力的一些基本做法.但問題解決能力是一種綜合能力,更需要我們教師在教學中不斷探索。

