運用改進的教學-模擬退火算法辨識關節臂式三坐標測量機的結構參數

夏軍勇 劉科進 鐘 飛 孫 穎

湖北工業大學機械工程學院，武漢，430068

0 引言

關節臂式三坐標測量機[1-3]具有質量小、使用方便、測量范圍廣等優點[2-4]，它一般由一個底座、兩個關節臂、三組旋轉關節及相應的零部件組成[5]。但是，不同于傳統的三坐標測量機，由于關節臂式三坐標測量機的測頭末端的坐標與其結構參數之間存在高非線性[2-3]的關系，所以其結構參數的較小變化就會引起測頭末端坐標較大的變化[6]，坐標誤差受結構參數的影響極大[4,7]。顯然，由于一系列因素的影響，使用一段時間后，其實際結構參數和標稱結構參數通常并不相等[6]，從而導致測頭末端的實際坐標并不等于用標稱結構參數計算出來的坐標。因此，當關節臂式三坐標測量機使用一段時間后，找到實際結構參數并將其重新植入控制設備中，從而準確地獲得測頭末端的實際坐標是迫切需要解決的問題。目前主要有兩種方法來減小關節臂式三坐標測量機測頭末端的坐標誤差并提高定位精度和降低運動不確定度[8-10]：①使用更高精度的零部件；②用合適的方法來辨識結構參數從而對其進行補償。但由于高精度零部件的制造成本很高，故使用高精度的零部件會大大增加制造成本，不利于它的推廣和廣泛應用。

基于以上分析，僅使用一個或幾個更高精度的零部件，既不經濟，也很難大幅度減小關節臂式三坐標測量機的測頭末端的坐標誤差[10-11]，因此，很有必要用合適的方法來辨識其結構參數。目前，主要的辨識方法是使用簡單的輔助工具結合合適的優化算法來進行。例如，FANG 等[12]使用基于量子行為的粒子群算法來辨識關節臂式三坐標測量機的結構參數；SANTOLARIA 等[13]用激光跟蹤儀建立多點定位系統并從激光跟蹤儀中獲取數據，從而辨識關節臂式三坐標測量機的結構參數；劉志等[14]將幾何搜索和結構參數辨識相結合，建立了兩邊辨識法；HAMANA 等[15]以球狀中心坐標測量系統作為測量工具來辨識關節臂式三坐標測量機的結構參數；KOVA等[16]用激光干涉儀和線性量規建立高精密測量系統來辨識并補償關節臂式三坐標測量機的結構參數；SANTOLARIA 等[13]在傅里葉多項式的基礎上，用標稱值和單點重復率誤差模型來辨識和補償關節臂式三坐標測量機的結構參數；王斌[17]建立了復合球坐標系并在此坐標系下通過點圓法和反轉法來辨識關節臂式三坐標測量機的結構參數，并用混合優化算法來辨識測頭的結構參數。

盡管有很多方法可辨識和補償關節臂式三坐標測量機的結構參數，但這些方法依賴于使用高精密的元器件，這些元器件極大地增加了設備的制造成本且受外部環境影響很大，會引起很大的測量不確定性。另外，使用高精密的元器件使得辨識程序復雜、不便操作，很大程度上增加了其復雜性。本文在單點重復率誤差的基礎上，將改進的教學算法和模擬退火算法進行融合，提出一種混合算法來對關節臂式三坐標測量機的結構參數進行辨識。首先，將錐型孔固定在基座上并將關節臂式三坐標測量機的測頭末端伸進錐型孔里面使其與錐型孔配合；其次，搖動關節臂式三坐標測量機到不同的位姿和構型以得到多組不同的關節轉角組合；再次，將得到的數據分別與教學算法、模擬退火算法和改進的教學-模擬退火算法結合來對關節臂式三坐標測量機的結構參數進行辨識以得到相應不同的辨識結果；然后，用辨識前后的關節臂式三坐標測量機再次進行單點重復率誤差實驗，得到相應的結果；最后，對相應的結果進行比較、分析和歸納從而得出結論。

1 運動學建模及分析

圖1是關節臂式三坐標測量機的物理結構圖和坐標系圖。

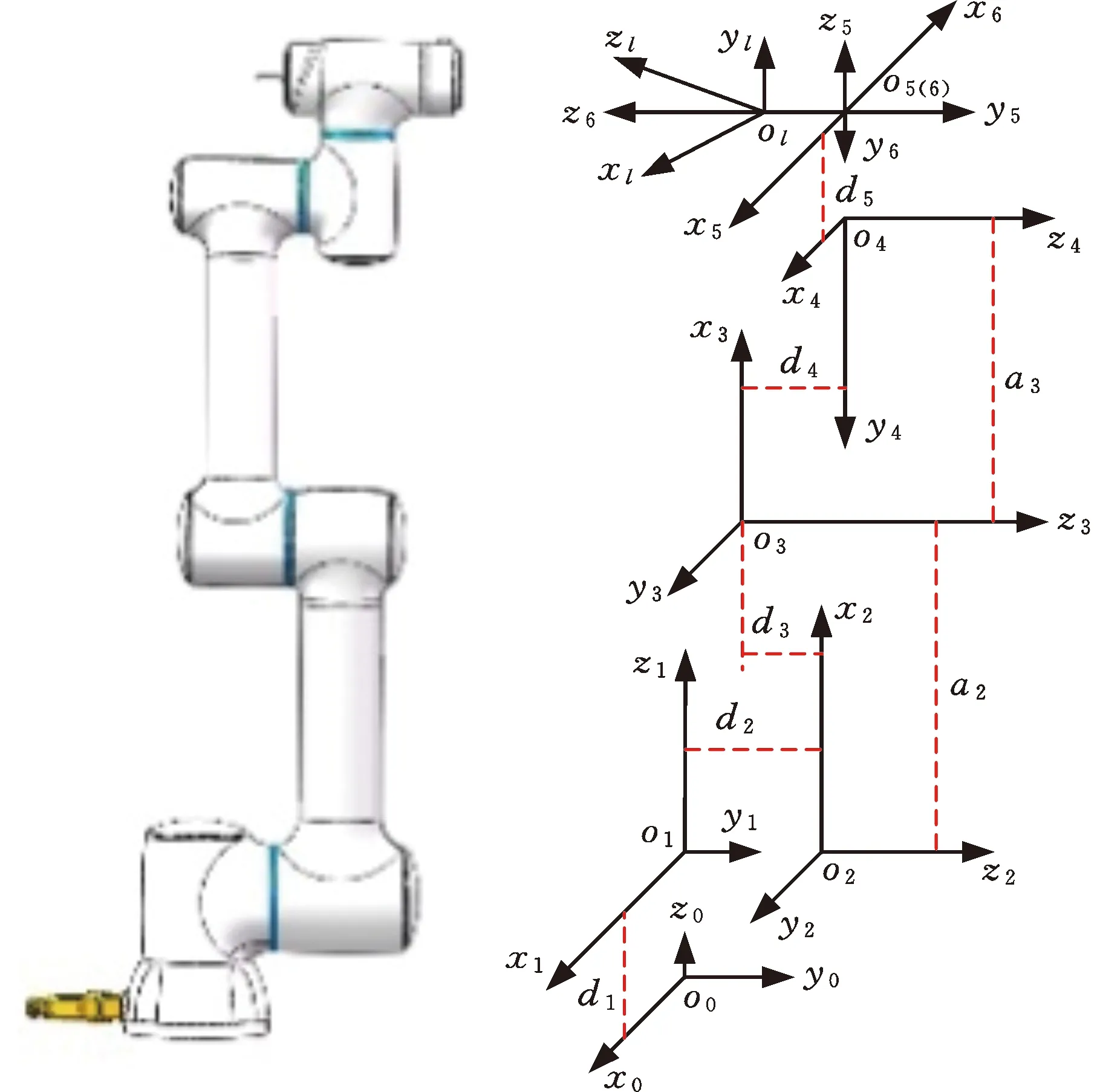
(a)結構圖 (b)坐標圖

在運動學中，關節臂式三坐標測量機的測頭末端的坐標可以通過一系列的矩陣變換得到。運動學建模的目的就是構建各關節轉角和測頭末端的坐標之間的傳遞函數。設i-1Ti表示第i個坐標系到第i-1個坐標系的變換矩陣，根據MDH模型[18]，第i個坐標系到第i-1個坐標系之間的傳遞函數為

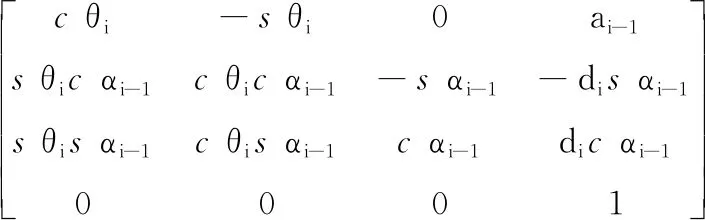
(1)

其中，θi、di、ai-1、αi-1、l分別是關節轉角、連桿長度、關節偏距、關節扭角和測頭長度；s表示sin，c表示cos。給出以上矩陣以后，關節臂式三坐標測量機的測頭末端在基坐標系中的坐標可表示為

(2)

其中，x、y、z分別是測頭末端在基坐標系中x軸、y軸和z軸三個方向的坐標。關節臂式三坐標測量機的標稱參數見表1。

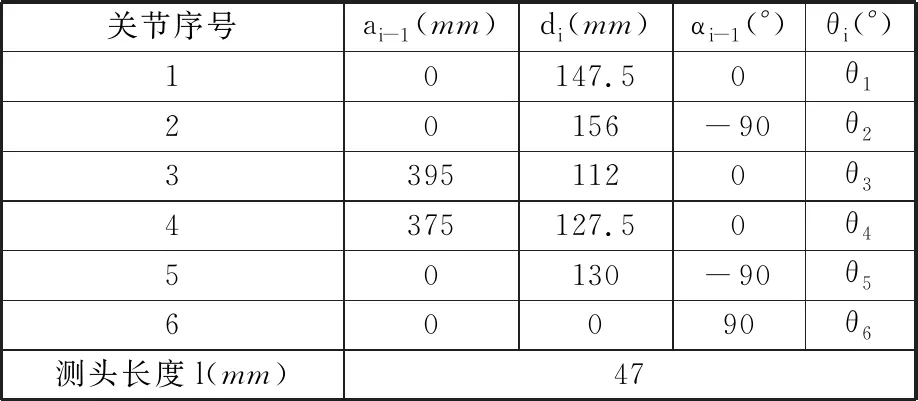
表1 關節臂式三坐標測量機的標稱參數

盡管關節臂式三坐標測量機有5組參數，但是只有關節轉角θi是動態變化的，其余4組參數均為常數，也被稱作結構參數。通常，這四組結構參數在出廠前由供應商辨識好并將其作為標稱結構參數。然而，由于一些因素的影響，當關節臂式三坐標測量機使用一段時間之后，其標稱參數發生了改變，這也會引起測頭末端坐標的誤差，故很有必要對關節臂式三坐標測量機的結構參數進行重新辨識。

2 相關分析和目標函數

測頭末端的坐標可以用式(2)計算。經過高精密儀器測量N種姿態下測頭末端的坐標Pk(kx,ky,kz)(k=1,2,…,N)及相應的關節轉角kθi(k=1,2,…,N;i=1,2,…,6)，則由式(2)可得

(3)

通過解這3N組方程，關節臂式三坐標測量機的實際結構參數就能被解出并被用作新的標稱結構參數。此方法理論上講是正確且可行的，但實際上，一方面式(3)是隱式方程，很難甚至幾乎不可能解出其解析解；另一方面，測頭末端的坐標是要通過高精密的儀器測量得到的，這就使得操作繁瑣并且很難實現。因此，本文采用單點重復率誤差的方法對其進行辨識。簡單來講，就是用關節臂式三坐標測量機在N種不同姿態下測量同一點的坐標得到N組關節轉角，再將這N組關節轉角和相關算法結合來對關節臂式三坐標測量機的結構參數進行辨識。

將關節臂式三坐標測量機的測頭末端插入錐型孔里面使其與錐型孔配合，然后搖動關節臂到N種不同姿態下，就可以得到N組不同的關節轉角kθi。設任意一組已知的結構參數為(di,ai-1,αi-1,l)，記為X=(di,ai-1,αi-1,l)，將X及kθi代入式(3)，得到測頭末端坐標的實際值與標稱值的差：

(4)

因在實際情況中，實際坐標(x,y,z)很難測量出來，所以用坐標的平均值來代替其實際值：

(5)

求出kE后，其平均值為

(6)

因kE的平均值不能反映這些數據的分布規律，所以引入其相應的標準差：

(7)

對于任意一組給定的結構參數X=(di,ai-1,αi-1,l),根據“3σ原則”，其目標函數定義為

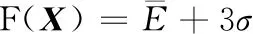
(8)

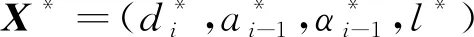
(9)

本文將式(8)定義為目標函數，并結合優化算法來尋找其最優解或可接受的解，將此最優解或可接受的解作為關節臂式三坐標測量機的實際結構參數。顯然，當X越接近X*時,F(X)越小。因此，后續算法的目的就是找到使F(X)為0或小于給定閾值的X0，此解就是需要找到的解。

3 改進的教學-模擬退火算法

3.1 教學算法

教學算法[19-21]是一種模擬教學行為機制的仿生群智能優化算法，其核心思想是模擬課堂中老師對學生的教學以及學生之間互相學習的行為機制，其運算機制主要分為兩個階段：教學階段和學習階段。

(1)教學階段。在教學階段，“教師”的位置保持不變，“學生”逐個地向“教師”學習并通過下式更新自己的位置：

Difference_Meant=rt(Mnew-TFMt)

(10)

Xnew,i=Xold,i+Difference_Meant

(11)

其中，t指整個群體進化到了第t代；rt是(0,1)之間的一個隨機數；Mnew是進化到當前代的“老師”；TF是群體平均值的改變因子；Mt是所有變量的均值，通過下式來計算：

(12)

式中，D為變量的維度。

(2)學習階段。在學習階段，第i個個體通過下式更新位置：

(13)

式中，fitness(·)是相應個體的適應度值；Xold,i、Xnew,i分別為第i個個體更新前和更新后的位置；r為(0,1)之間的隨機數。

盡管教學算法沒有參數需要設定，運算機制比較簡單，但是它的尋優速度不快，并且尋優精度不高。特別是對于像本文中這種多變量高維高非線性的問題，算法對其進行尋優的時候會急劇增加算法的運算量和運算時間，大幅降低其效率。為避免此弊端，本文對教學算法進行改進從而得到改進的教學算法來加快其尋優速度。

3.2 改進的教學算法

鑒于教學算法的這種特點，本文對其“教學階段”和“學習階段”都有所改進，以加快其收斂速度。在教學階段，分別做如下改進。

(1)動態更新“教師”角色。即當每個 “學生” 向 “老師” 學習完后，就比較該學習完的 “學生” 和當前 “老師” 的適應度值，選擇兩者中適應度值較好的個體作為新的 “老師”。更新機制如下：若fitness(Xnew,i)≥fitness(Mnew)，則Mnew=Xnew,i。其中，Xnew,i是第i個個體更新后的位置，Mnew是當前代的 “老師”。

(2)改變教學更新公式。在 “教學階段” ，“學生” 向 “老師” 學習的公式為

Xnew,i=Xold,i+Difference_Meani+cr(gbesti-Xold,i)

(14)

式中，c為(0,1)之間的隨機數；gbest為歷史最優個體。

在學習階段，做如下改進：“學生”之間通過互相學習，第i個個體的位置更新公式為

(15)

式中，r1、r2為學習因子，本文均取2。

3.3 改進的教學-模擬退火算法

雖然改進的教學算法具有較快的收斂速度，但是在增加收斂速度的同時會降低收斂精度，使算法陷入局部最優區域。模擬退火算法[22]是一種對固體的退火過程進行模擬的仿生智能優化算法，由于它采用Metropolis接受準則，所以當群體陷入局部最優區域以后，它能通過Metropolis接受準則的特殊機制將陷入局部最優區域的群體“拽出來”，從而讓群體在更廣闊的新區域重新尋優，進而達到找出全局最優個體的目的。基于模擬退火算法的這種特殊的尋優機制，本文就利用這種特殊機制來擴充在改進的教學算法階段陷入局部最優區域的解；利用此特性將這個不能接受的最優解“拽出來”，接著到更廣闊的空間來繼續尋優，從而以更大的概率來找到問題的全局最優解。兩種算法的轉換靠收斂精度轉換準則來連接。

在本文各算法中(教學算法、改進的教學算法、模擬退火算法和改進的教學-模擬退火算法)，個體的適應能力由其適應度值來度量，即具有較大適應度值的個體有更大的幾率來執行后續操作并產生下一代。就目標函數而言，使目標函數值越小的個體越優良，所以適應度函數定義成以下形式:

(16)

式中，rlim是一個極小的正數，以保證分母不為0。

改進的教學-模擬退火算法的基本原理如下。

(1)轉換準則的設計。設t、Xbest(t)和fitness(Xbest(t))分別是當前進化代數、到目前為止的最優個體和最優個體的適應度值，那么轉換準則設計為下式的關系：

(17)

其中，K是一個正整數，ε和δ是轉換閾值，并且，K、ε和δ都是提前給定的常數。以上條件說明，如果在改進的教學算法階段得到的最優解Xbest(t)滿足式(17)，則改進的教學算法終止，算法進入模擬退火階段，在模擬退火階段進一步擾動在改進的教學算法階段得到的最優解 。這兩種算法通過這種機制連接起來以后得到的新算法在本文中稱為改進的教學-模擬退火算法。

(2)終止條件的設定。對于某個智能優化算法，如果到目前為止所找到的最優解Xbest(t)不是設備的實際結構參數(或不能作為可接受的解)，或者混合智能優化算法進化了很多代以后隨著迭代次數的增加其最優解基本不再變化，那么可以認為此算法尋優失敗，應當終止此算法的運算，從而避免不必要的冗余計算，減少運算量和時間。在本文中，終止條件設定為

F(Xbest(t))≤η

(18)

或

fitness(Xbest(t))≥τ

(19)

或

t≥G

(20)

其中，G是最大迭代次數；η和τ都是結束算法運算的閾值。本文中，相關參數設定如下：種群數量M=100；G=40000；K=30；ε=0.1；δ=0.2；T0=104；Markov鏈的鏈長J=30；終止溫度Te=10-3；溫度衰減函數μ=0.9。

4 實驗結果及討論

4.1 實驗

當獲取一系列關節轉角以后，將其分別與教學算法、模擬退火算法和改進的教學-模擬退火算法相結合而進行尋優操作來優化關節臂式三坐標測量機的結構參數。用教學算法、模擬退火算法和改進的教學-模擬退火算法辨識關節臂式三坐標測量機的結構參數的流程框圖分別見圖2～圖4。

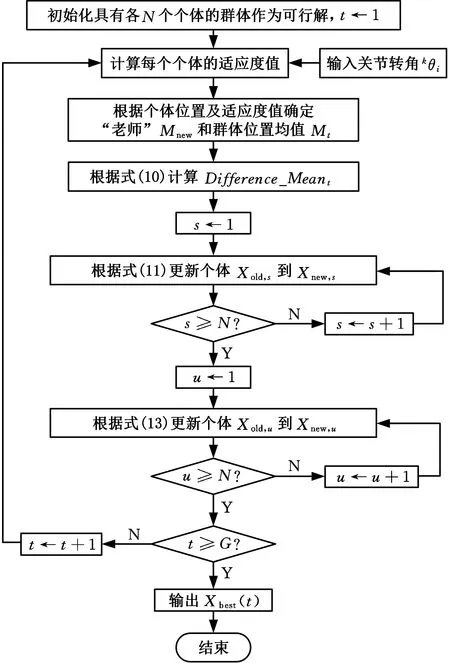
圖2 用教學算法辨識關節臂式三坐標測量機的結構參數流程圖

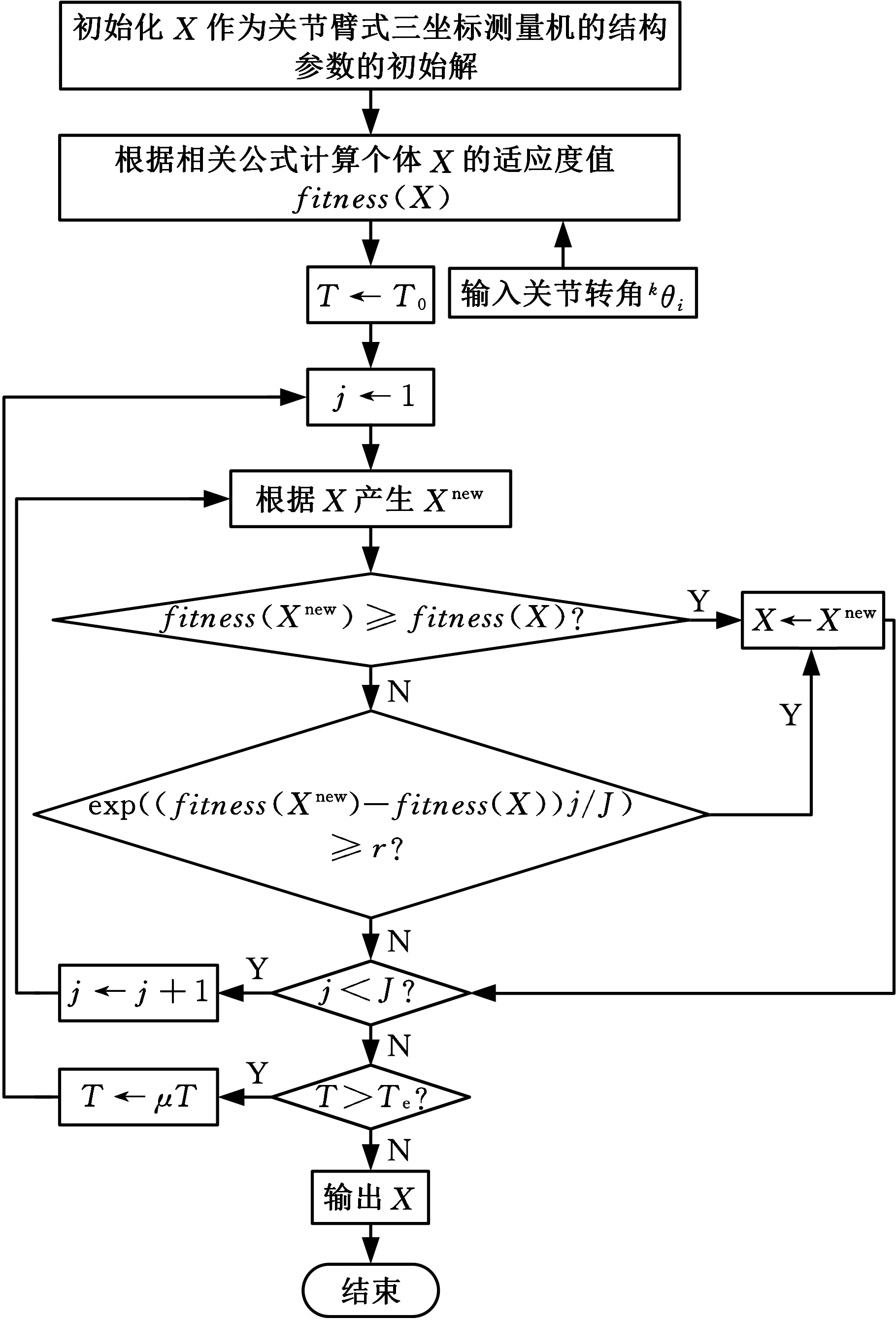
圖3 用模擬退火算法辨識關節臂式三坐標測量機的結構參數流程圖

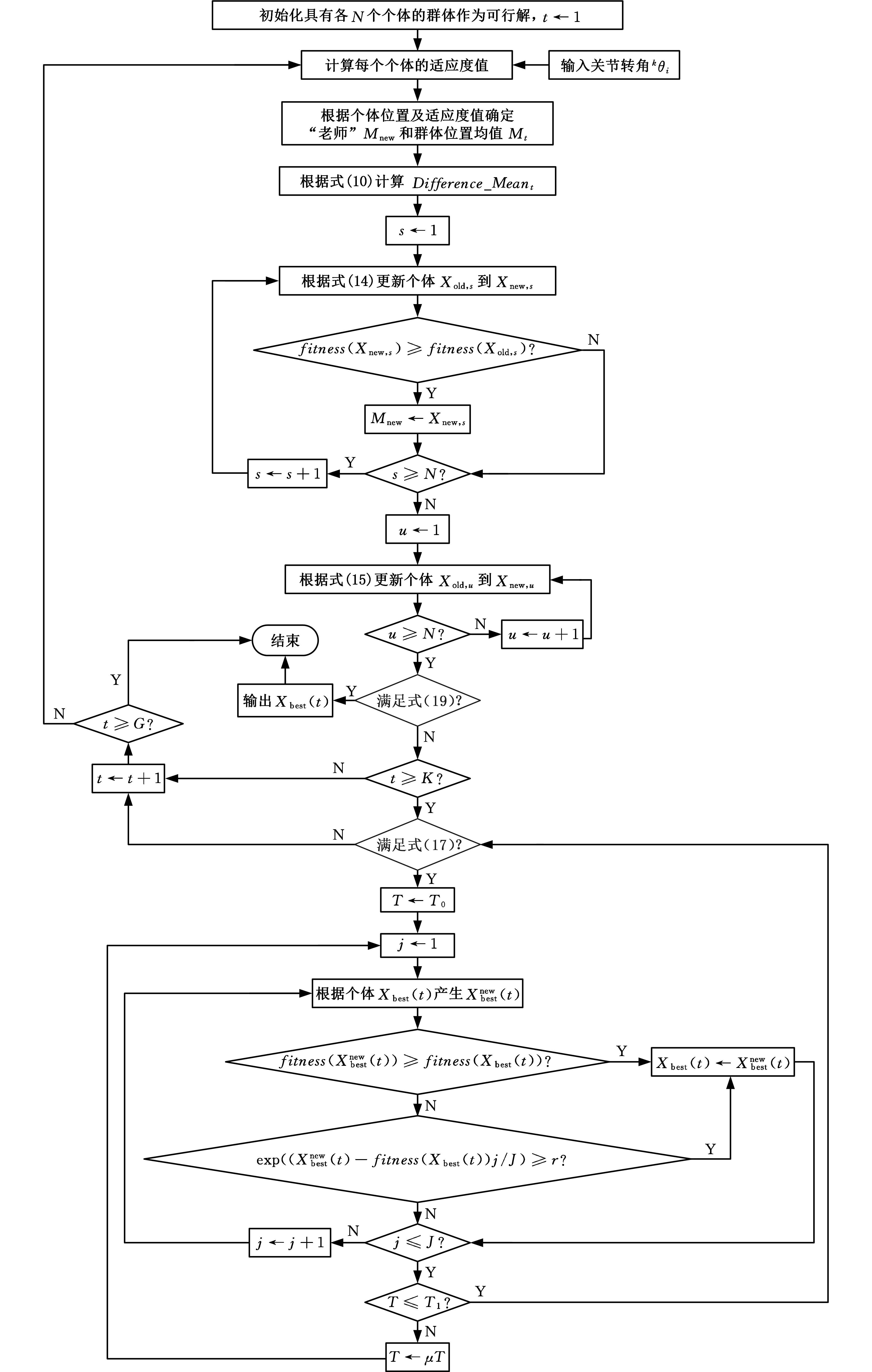
圖4 用改進的教學-模擬退火算法辨識關節臂式三坐標測量機的結構參數流程圖

如果某個最優解Xbest(t)滿足式(18)或式(19)，就認為算法尋優成功，即認為此時算法找到了關節臂式三坐標測量機的結構參數的實際值，并且將此個體Xbest(t)記為Xopt。需要注意的是，由于一些誤差原因，由算法和測得的基本數據所導出的全局最優個體Xopt一般不等于但無限接近實際值。

由于在算法執行的過程中，相關變量會經過一系列的運算操作，這可能會導致其越過對應的邊界值。本文中，由于長度結構參數是非負數并且ai-1(i=1,2,5,6)、d6和αi-1(i=1,3,4)為0，所以ai-1(i=1,2,5,6)和d6的搜索變化范圍設定為(0,10)；ai-1(i=3,4)和di(i=1,2,…,6)設定為(0，±10)；αi-1(i=1,2,…,6)設定為(0，±10°)；l設定為(0，10)。當結構參數的某個變量y越過其對應的邊界值時，則由隨機函數發生器rand生成新變量，具體生成機制如下：

若y越過相應的邊界，則

y=(ulim-llim).*rand+y

式中，ulim、llim分別為相應變量的上界和下界。

為便于比較，繪制了最優個體Xbest(t)的適應度F(Xbest(t))的進化曲線。用教學算法、模擬退火算法和改進的教學-模擬退火算法辨識關節臂式三坐標測量機時，將最優個體Xbest(t)的適應度F(Xbest(t))的進化曲線都畫在一個坐標系中，其進化曲線如圖5所示。用三種算法辨識關節臂式三坐標測量機后所得的關節臂式三坐標測量機的結構參數分別見表2～表4。

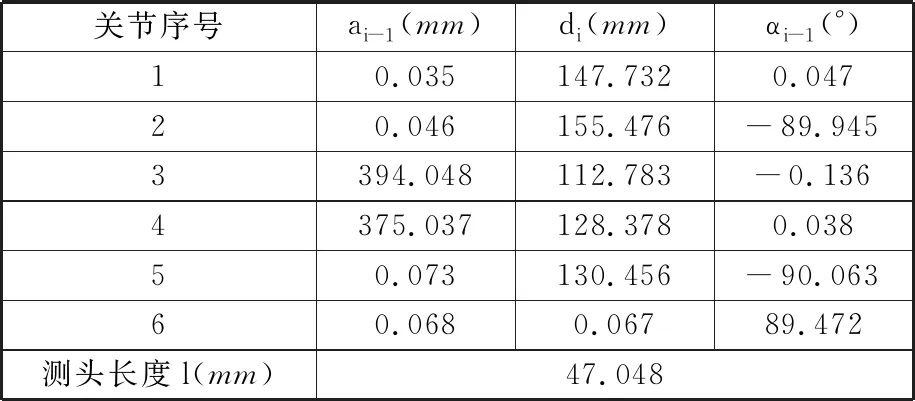
表4 用改進的教學-模擬退火算法辨識關節臂式三坐標測量機后得到的結構參數

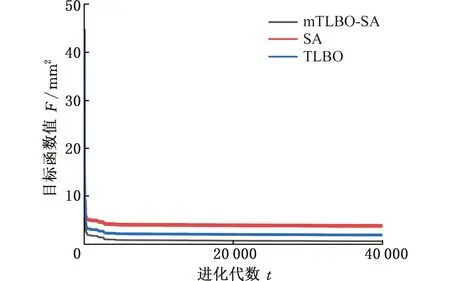
圖5 用不同的算法辨識關節臂式三坐標測量機的結構參數時目標函數的進化曲線

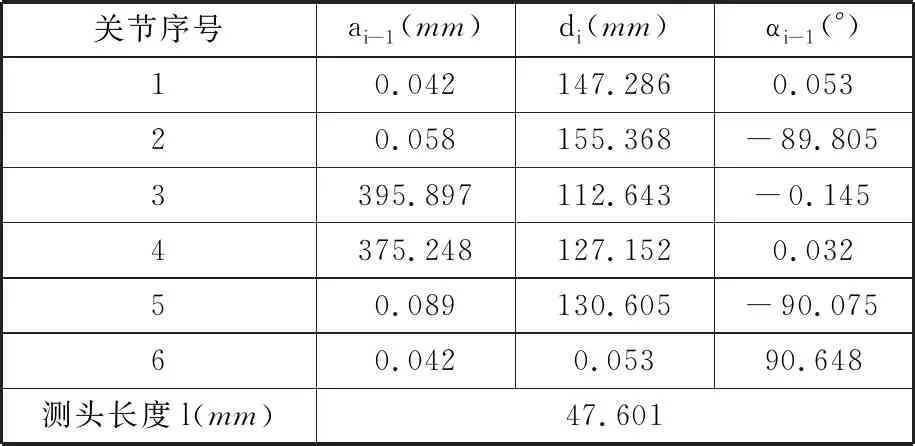
表2 用教學算法辨識關節臂式三坐標測量機后得到的結構參數

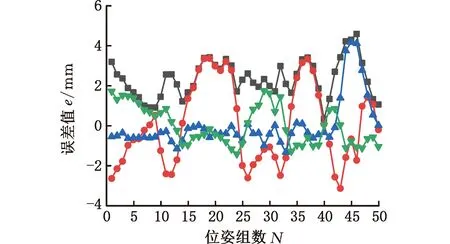
用三種算法分別尋優得到關節臂式三坐標測量機優化的結構參數以后，將三組優化后的結構參數分別植入關節臂式三坐標測量機的控制器中作為其新的標稱結構參數。為便于分析和比較，分別用辨識前和辨識后的關節臂式三坐標測量機進行新的單點重復率誤差實驗。如圖6所示，單點被重復測量多次，其單點重復率誤差曲線如圖7所示。

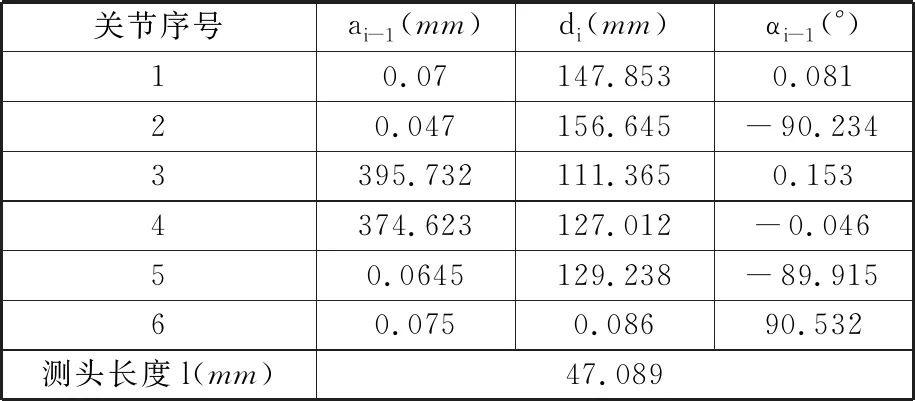
表3 用模擬退火算法辨識關節臂式三坐標測量機后得到的結構參數

(a)全局圖

(a)辨識前

4.2 結果

(1)觀察圖5可知，隨著迭代次數的增加，目標函數值逐漸趨向于0。

(2)觀察圖7可以得到以下兩組指標并分別以表格的形式列出結果：① 辨識前后單點重復率誤差值的最大值、最小值、平均值和標準差及其在三個方向上的對應分量；② 經過TLBO、SA和mTLBO-SA辨識后單點重復率誤差值的最大值、最小值、平均值和標準差及其在三個方向上減少的百分比對應分量的下降率。

其中，辨識前后的單點重復率的誤差值見表5；辨識前后的單點重復率誤差值分別在x、y和z方向的分量見表6～表8；經過TLBO、SA和mTLBO-SA辨識后單點重復率誤差值的下降率見表9；經過TLBO、SA和mTLBO-SA辨識后單點重復率誤差值的下降率在x、y和z方向的分量分別見表10～表12。

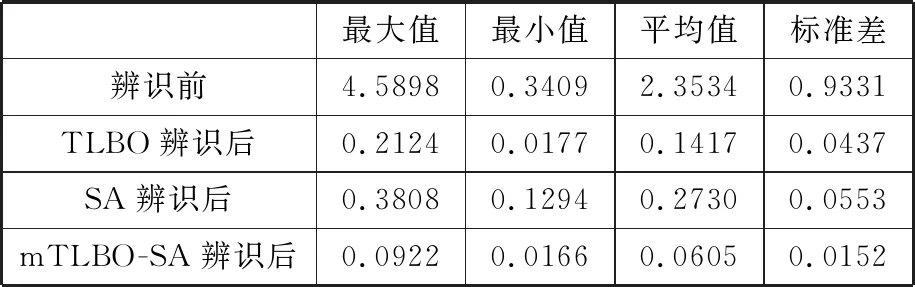
表5 辨識前后的單點重復率誤差

表6 辨識前后單點重復率誤差在x方向的分量

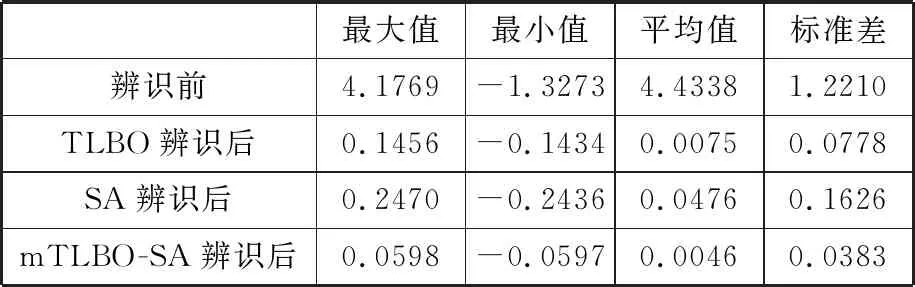
表7 辨識前后單點重復率誤差在y方向的分量

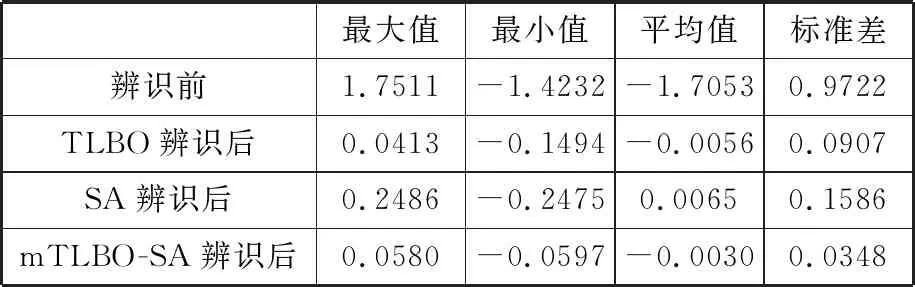
表8 辨識前后單點重復率誤差在z方向的分量

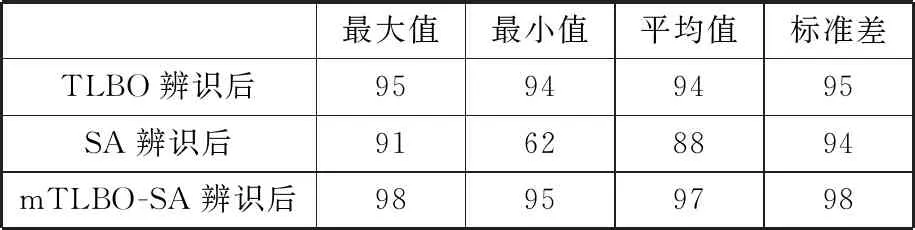
表9 辨識后單點重復率誤差下降率

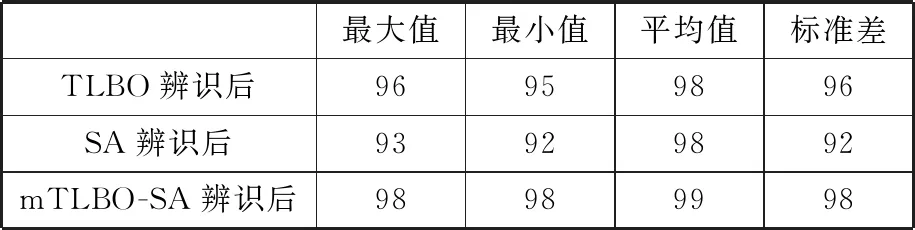
表10 辨識后單點重復率誤差下降率在x方向的分量

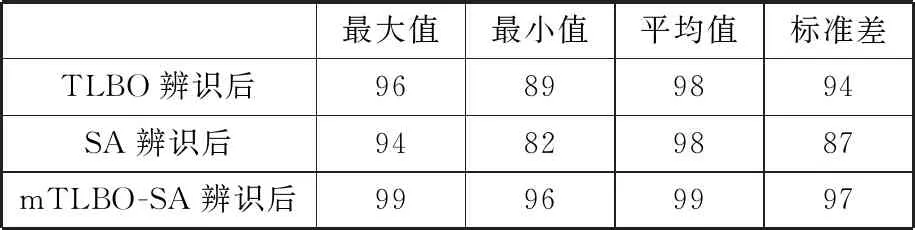
表11 辨識后單點重復率誤差下降率在y方向的分量

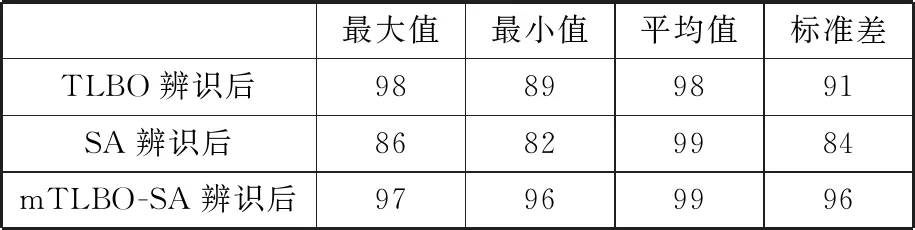
表12 辨識后的單點重復率誤差下降率在z方向的分量

4.3 討論

(1)通過教學算法、模擬退火算法及改進的教學-模擬退火算法辨識后，關節臂式三坐標測量機的單點重復率誤差值及其在三個相應坐標軸方向上的對應分量均有不同幅度的減少。

(2)經過教學算法辨識后，單點重復率誤差值及其在三個相應坐標軸方向上對應分量的減幅從89%到98%不等；經過模擬退火算法辨識后，單點重復率誤差值及其在三個相應坐標軸方向上對應分量的減幅從62%到98%不等；經過改進的教學-模擬退火算法辨識后，單點重復率誤差值及其在三個相應坐標軸方向上對應分量的減幅從95%到99%不等。

(3)除極個別情況以外，經過mTLBO-SA辨識后單點重復率誤差值的各減少幅度都超過96%，并且各減幅比經過TLBO和SA辨識后對應的減幅最少多1%，最大多33%，一般情況下也會多3%～15%。

5 結論

(1)實際情況中，很難測量到關節臂式三坐標測量機的實際結構參數，僅僅使用一些單一的傳統算法很容易使算法陷入局部最優區域從而尋優失敗。

(2)無論是用教學算法還是模擬退火算法對關節臂式三坐標測量機的結構參數進行辨識，算法都可能會陷入局部最優區域或者早熟，使得優化后的單點重復率誤差值不能很好地大幅減小。

(3)通過SA對mTLBO擾動后，算法能在新的區域進行新的尋優操作，這不僅使算法跳出局部最優區域，還能增加群體的多樣性，使得群體以更大的概率找到或更接近全局最優解。

(4)通過對比各結果不難發現:mTLBO-SA更適合關節臂式三坐標測量機的結構參數辨識，能更有效且高效地提高關節臂式三坐標測量機的精度和降低其運動不確定度。