基于時空注意力網絡的動態高速路網交通速度預測

鄒國建，賴子良，李曄

（1.同濟大學 道路與交通工程教育部重點實驗室，上海 201804；2.同濟大學 交通運輸工程學院，上海 201804）

0 概述

高速公路速度預測對于智能交通系統（ITS）至關重要，可為出行者和交通管理部門預先提供有用的交通信息［1］。目前，高速公路交通速度預測研究主要聚焦于短時預測，對于長時間速度預測能力略顯不足［2］。根據交通速度預測研究的特點，可以將現有的研究方法分為統計方法、傳統機器學習方法和深度學習方法三類。

統計方法成功應用于交通速度預測任務，包括歷史平均模型（HA）和自回歸綜合移動平均模型（ARIMA）［3-5］。HA 使用同一時間的歷史數據的平均值作為未來預測任務中相同時刻的預測值［3］。ARIMA 作為傳統的時間序列預測方法，結合了移動平均和自回歸分量來對歷史時間序列數據進行建模［4-5］。然而，由于交通速度具有非線性的性質，參數化方法基于先驗知識、理論假設和簡單的數學統計，在精準預測交通速度方面表現不佳。

傳統機器學習方法緩解了統計方法遇到的難題，此類方法通過提取交通大數據中的非線性特征來提高預測的精準度［6-10］，如：VANAJAKSHI等［6］提出一種支持向量機（SVM）的回歸技術用于交通速度的短期預測；JIANG等［7］使用隱馬爾可夫模型（HMM）來表現單個車輛的速度與路段交通速度之間的統計關系；SHIN等［8］提出一種基于隨機模型的車速預測算法，使用具有速度約束的馬爾可夫鏈作為基礎；ZHANG等［9］提出一種基于高階多元馬爾可夫模型的交通因素狀態網絡模型（TFSN）來建立速度與相關因素之間的關系。然而，傳統機器學習方法主要提取淺層數據特征，無法對復雜的交通路網時空數據特征進行深度建模［2，7-9］。

相比傳統機器學習算法，深度學習技術在處理復雜的非線性交通數據方面優勢更為明顯［11-14］，在相關研究中：CSIKóS［11］等使用人工神經網絡（ANN）進行交通速度預測；JIA等［12］提出深度信念網絡（DBN）模型用于短時交通速度預測；TANG等［13］提出一種基于改進模糊神經網絡（FNN）的交通速度預測模型。然而，這些方法處理復雜的交通路網時空數據特征能力有限，迫切需要更為有效的深度學習方法。

循環神經網絡（RNN）是一種用于時間序列預測任務的深度學習方法，可以有效提取數據的時間關聯特征［15］。目前，許多交通速度預測任務使用RNN 作為時序特征提取器來提高預測精準度［16-20］，在相關研究中：GU等［17］建立一種基于長短期記憶（Long Short-Term Memory，LSTM）網絡和GRU 的新型融合深度學習（FDL）模型，以捕捉車道短時速度預測的時空特征；WANG等［18］使用雙向長短期記憶神經網絡對每個關鍵路段進行建模的方法（Bi-LSTM NN），使用堆疊Bi-LSTM 層來合并時間信息。上述方法使用RNN 作為特征提取器來提取交通數據的時間的相關性，但是忽略了數據的空間相關性對預測產生的影響。為解決RNN 遇到的問題，基于CNN 的時空預測模型被廣泛應用于交通速度預測任務中［21-27］，在相關研究中：為捕捉復雜的動態交通信息，ZHOU等［25］提出一種稱為時空深度張量神經網絡（ST-DTNN）的速度預測方法，主要用于混合道路類型的大規模城市網絡；YANG等［26］提出基于路徑的速度預測神經網絡（PSPNN），其由CNN和雙向LSTM（Bi-LSTM）網絡組成，用于提取歷史數據的時空特征，實現基于路徑的速度預測；ZANG等［27］提出一種基于CovLSTM 的多尺度時空特征學習網絡（MSTFLN），用于高架公路長期交通速度預測的研究任務。然而，傳統的CNN 只適用于歐幾里得空間結構數據，而交通數據具有非歐幾里得空間性質。因此，基于CNN 的交通速度數據空間特征提取存在較大的缺陷。

最新研究將CNN 擴展到可以處理非歐幾里得空間結構數據的圖卷積神經網絡（GCN）［28］，并且已成功應用于交通預測任務中，其中包括交通速度預測［29-31］。高速路網中每條道路之間的相關性隨著時間動態變化，而GCN 受限于捕獲高速路網的動態空間相關性。考慮到圖注意力網絡（GAT）可解決動態的空間相關性問題［32］，本文提出一種基于時空注意力網絡的動態高速路網速度預測模型（ST-ANet），結合GAT 和LSTM 設計高速公路網絡時空特征提取塊（GLSTM-block）。首先使用基于空間注意力機制的GAT 網絡提取高速路網的動態空間相關性，然后通過LSTM 網絡提取輸入數據和GAT 輸出特征的時間相關性，最后基于時間注意力機制計算歷史輸入數據和預測值之間的時間相關性。

1 高速公路速度數據

本文的研究區域為中國寧夏回族自治區銀川市濱湖新區的高速路網，如圖1 所示，共采集8 個高速公路收費站的ETC 行車數據，包括49 條高速公路路段的交通速度數據。高速公路交通速度數據包括速度、時間和道路位置三個因素，時間跨度為2020 年5 月1 日—2020 年8 月31日。每隔1 h 采樣一次，得到交通速度數據的時間序列形式{xti|-∞＜ti＜+∞}，其中：xti∈?N×3；N表示道路的條數。道路位置不隨時間變化，共有49 條道路，即49 個位置索引。本文使用80%的數據作為訓練集，20%的數據作為測試集。

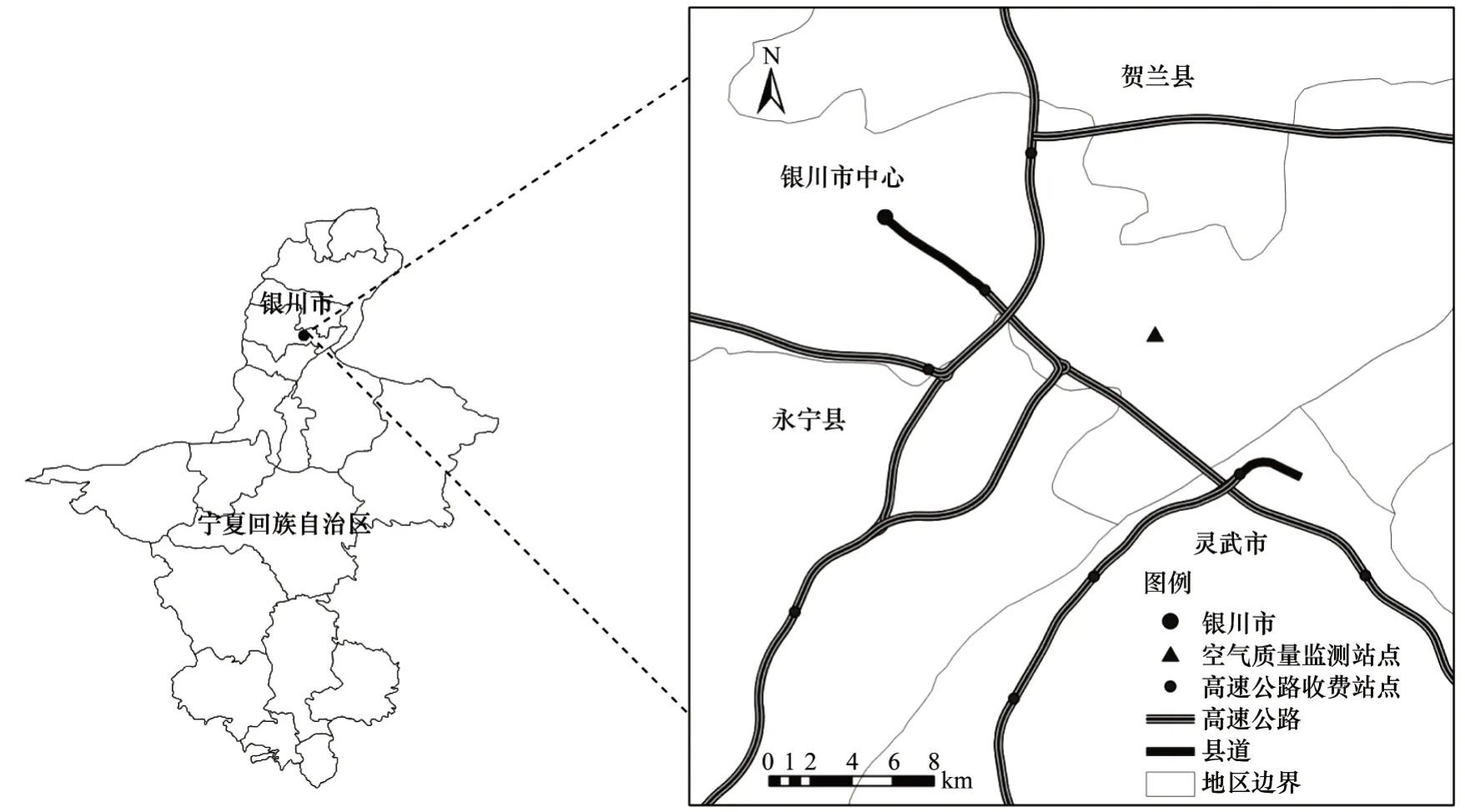
圖1 研究區域Fig.1 Study area

2 ST-ANet 模型

2.1 問題定義

本文的研究目標是：預測高速公路網絡中每一條道路未來一段時間內的交通速度情況。將輸入的高速路網圖定義為G=(V，E，A)，其中：V代表節點集；E表示邊集；A∈?N×N，表示鄰接矩陣；N表示節點的數量。需要特別強調的是高速路網圖，本文將每條道路抽象為圖中的節點，將道路的連接抽象為邊，每條線段代表一條高速公路，每條道路都可以映射為圖網絡節點。鄰接矩陣A表示道路之間連接關系，1 表示兩條道路之間存在連接，0 表示沒有連接。假設輸入時間步長為P，預測時間步長為Q，且ti∈{t1，t2，…，tP，…，tP+Q}。本文研究問題的核心是如何揭示高速路網交通數據的時空相關性。因此，使用ST-ANet來學習隱藏在公路交通數據中的時空特征，實現高速路網交通速度的精準預測。本文以有4 條道路的高速公路網絡為例，如圖2 所示（彩色效果見《計算機工程》官網HTML 版）。其中：圖2（a）表示物理高速路網，每條道路由不同的字符和顏色表示；圖2（b）為高速路網的圖表示，道路用節點表示。

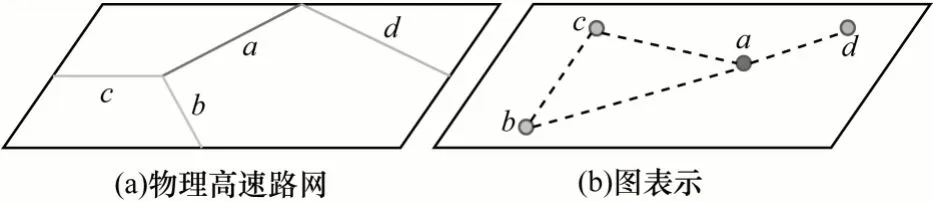
圖2 高速路網示例Fig.2 Example of expressway network

2.2 模型框架

針對時空特征提取和長期公路交通速度預測，本文提出ST-ANet 預測模型，模型框架如圖3 所示（彩色效果見《計算機工程》官網HTML 板），其中包含編碼器和解碼器2 個部分，編碼器用于提取輸入數據的時空特征，解碼器用于預測未來高速公路交通速度。

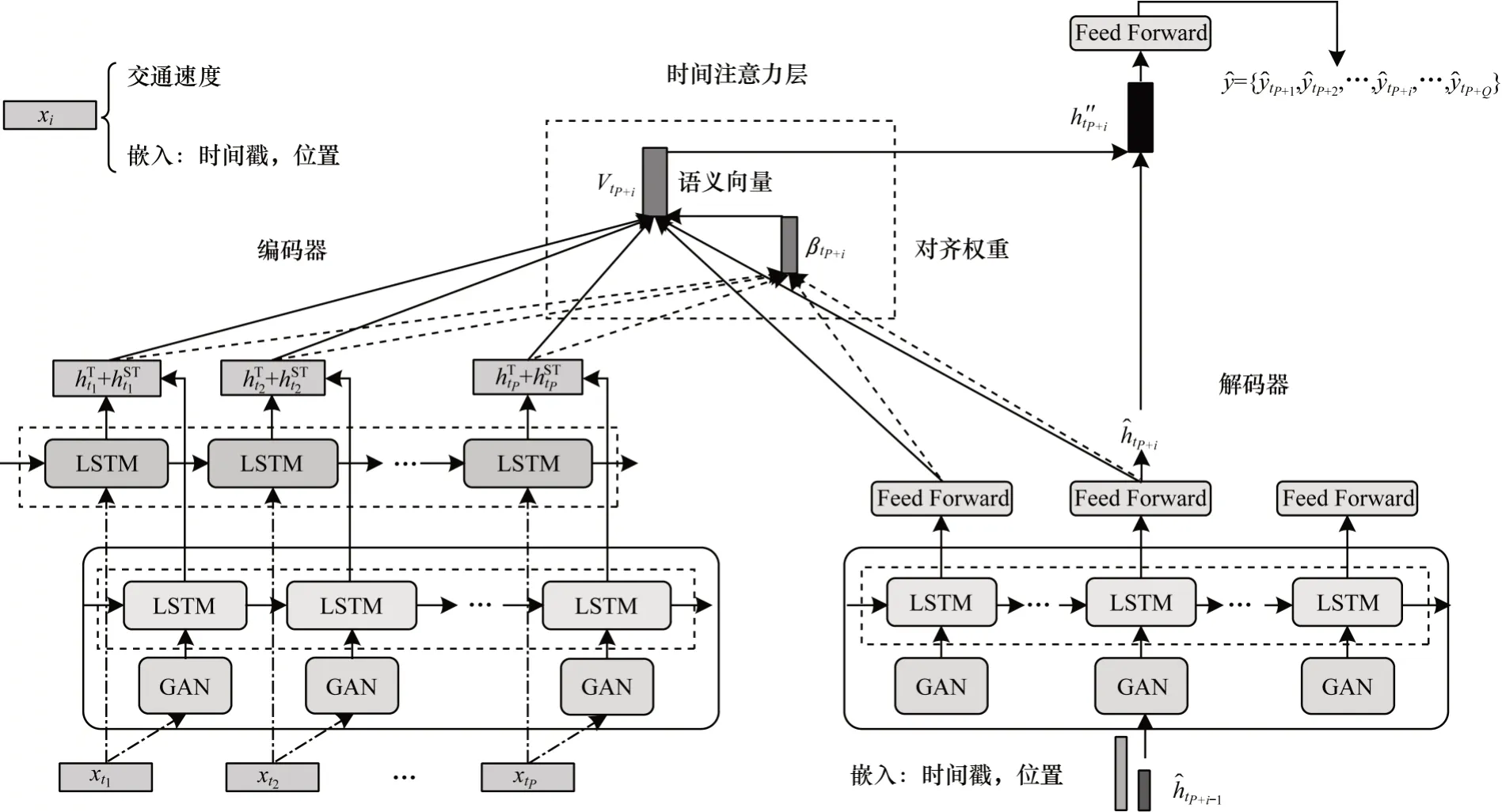
圖3 ST-ANet 預測模型框架Fig.3 Framework of ST-ANet prediction model

1）編碼器。公路交通數據x={xt1，xt2，…，xtP}，xti∈?N×dmodel以流水方式饋入到ST-ANet中，通過GLSTM-Block 學習每個時間步的時空特征。GAT 提取輸入交通數據的動態空間相關性，使用LSTM 提取GAT 輸出的空間特征的時間相關性。

2）解碼器。基于編碼器輸出，解碼器使用基于GLSTM-Block 的解碼器來預測長期高速公路交通速度。在整個解碼器預測過程中，使用時間注意力機制來計算歷史輸入數據與每個時間步預測值之間的相關性。

對于本文提出的ST-ANet，為整個網絡添加了密集連接和層歸一化技巧，以防止網絡信息丟失和內部協變量偏移問題。下文將詳細描述ST-ANet 模型每個部分的實現過程。

2.3 嵌入層

每個節點包含3 類數據信息，包括位置信息、時間戳信息和交通速度信息。輸入變量可拆分為3 種類型的嵌入表示，包括位置嵌入、交通速度嵌入和時間戳嵌入（小時、周、月）∈?N×d。時間戳和位置嵌入方法與Transformer 的嵌入方法相同，通過one-hot映射到稠密矩陣［33］。交通速度嵌入方法通過線性變換完成。對于每一個類型數據嵌入，數據維度可表示為d=dmodel/ 3=64。

2.4 GLSTM-Block

GLSTM-Block 由動態空間特征提取器和時間特征提取器兩個關鍵部分組成。在本例中，高速路網表示為圖（Graph）。在高速路網中，每條道路的通行速度受全局道路通行速度的影響，并且不同時期的影響權重w不同，定義為動態空間相關性。使用多層GAT 捕捉高速路網的動態空間相關性。此外，對于不同的時間步，同一條道路具有時間相關性，表現出動態連續變化的特性，定義為時間相關性。使用多層LSTM 來捕捉高速路網的動態時間相關性。GLSTM-Block 整體框架如圖4 所示（彩色效果見《計算機工程》官網HTML 版），其中⊕和?分別表示按元素求和和矩陣乘法。

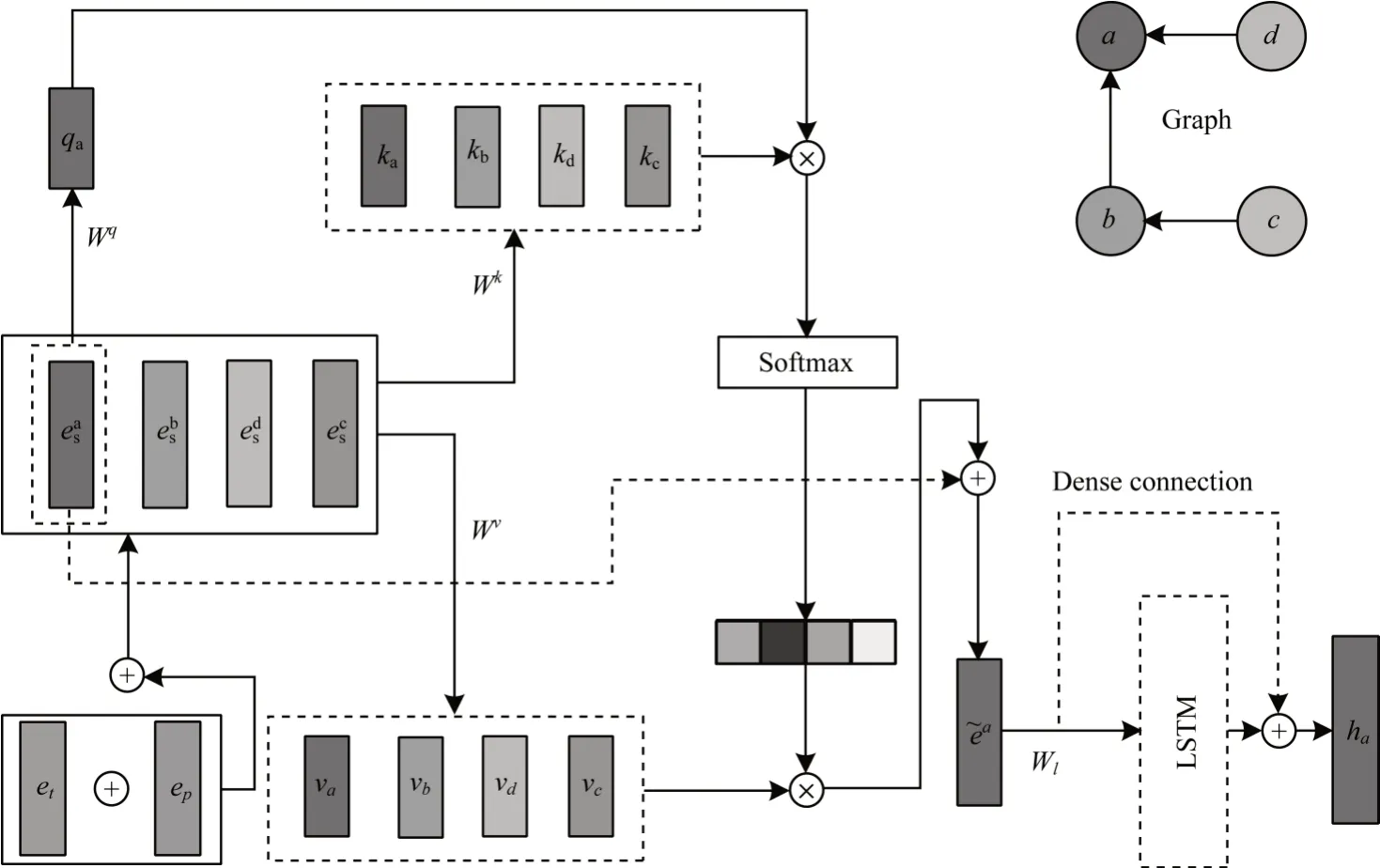
圖4 GLSTM-Block 框架Fig.4 Framework of GLSTM-Block

由于本文將會高頻使用非線性變換函數，因此首先將其定義為：

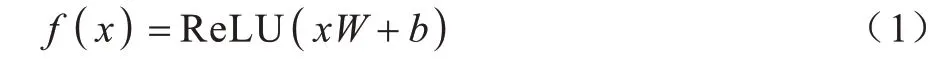
其中：x代表輸入變量；W和b代表可學習參數；ReLU 代表非線性激活函數。

1）動態空間特征提取器

本文使用GAT 在每個時間步ti提取高速公路網絡圖中任意節點vj的動態空間相關性，如圖5 所示（彩色效果見《計算機工程》官網HTML 版）。其中，圖例使用 2 層 GAT 提取高速公路交通數據的動態空間相關性，每層獲取全局空間相關性特征。

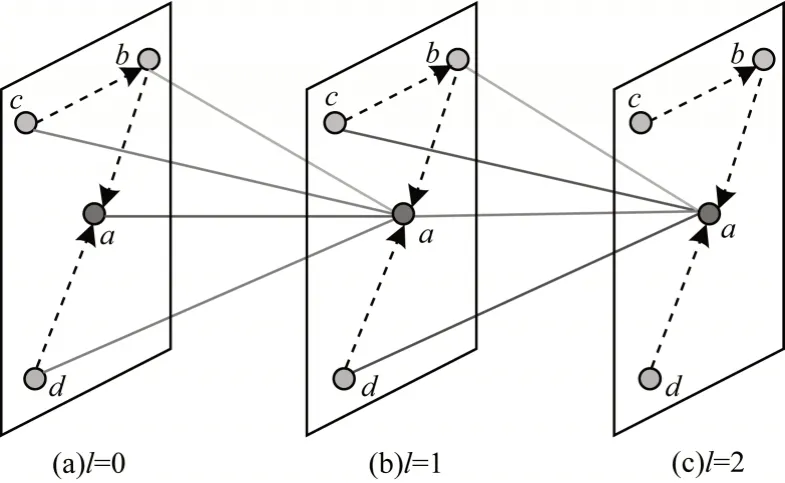
圖5 動態空間關聯特征提取過程Fig.5 Dynamic spatial correlation feature extraction process

對于案例圖節點vj，輸入為，動態空間相關性可以通過多頭自注意力機制計算得到［33］。所有節點V對節點vj的影響可通過第k頭自注意力計算得到，如式（2）所示：

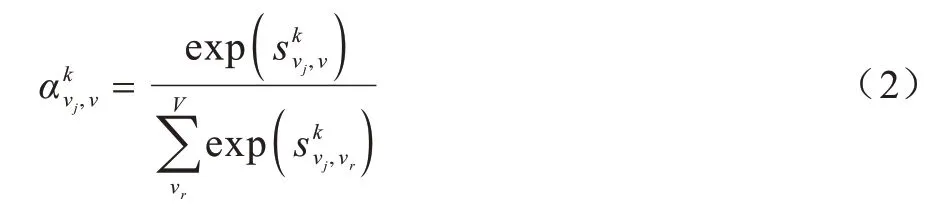
其中：表示節點vj與節點v之間的相關性。

相關性可以通過節點vj的查詢向量和v的鍵向量的內積得到，如式（3）所示：

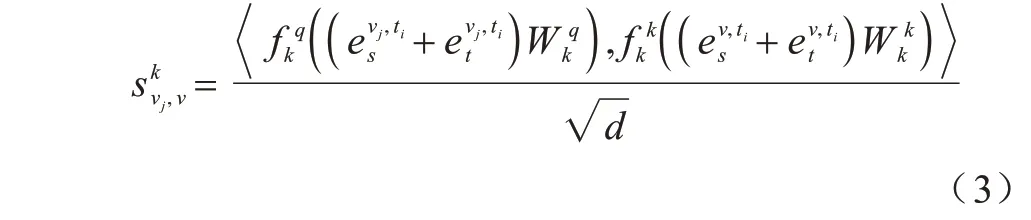
在獲得影響權重后，節點vj的隱藏狀態可以通過以下公式計算：

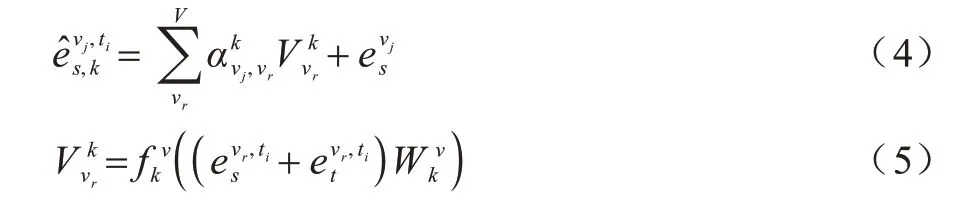
節點vj的動態空間相關性通過式（4）計算后，多頭注意力被使用。多頭注意力允許模型關注來自不同高速道路不同子空間的信息。并行M頭注意力機制并行計算，拼接不同的子空間信息，vj新的隱藏狀態可以通過式（6）更新得到：

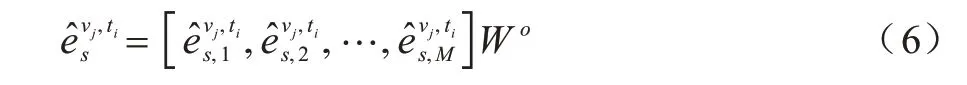
其中：Wo∈?Md×d表示映射層，它可以幫助模型整合高速道路vj所有相關方面的空間相關性。

在ti時間步，每條路vj的空間相關性可以通過式（1）～式（6）計算得到，并且整個路網的輸出為∈?N×d，如式（7）所示：

其中：表示動態空間相關性提取器的輸出；Wl∈?d×d。

2）動態時間特征提取器

時間相關性是高速公路交通數據的重要特征之一，以往的研究主要從時間維度展開［11，17］。LSTM 是時間特征提取的主流方法，本文將其用作時間特征提取器。多層LSTM 被用來捕獲公路交通數據的時間相關性。時間特征提取器的工作過程如圖6所示。

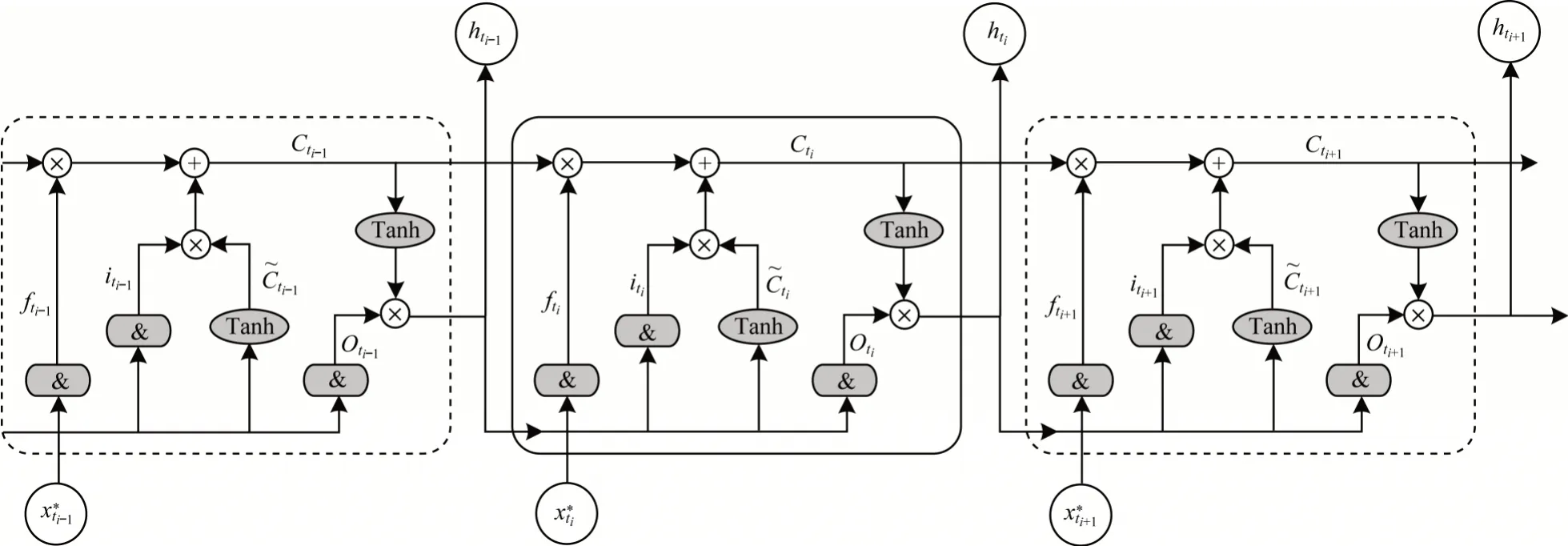
圖6 LSTM 模型結構Fig.6 LSTM model structure

對于節點vj，空間特征提取器的輸出為使用LSTM 提取其時間特征。假設i、f、o分別代表輸入門、遺忘門和輸出門，是每個時間步ti的輸入，hvj，ti是每個 時間步ti的輸出，σ代表 sigmoid 函數，tanh 代表 Tanh 函數，W和b分別代表 LSTM 的權重和偏置參數。時間相關性的提取過程如下：

步驟1LSTM 選擇性地忘記時間步ti時細胞狀態cvj，ti-1的特征信息：

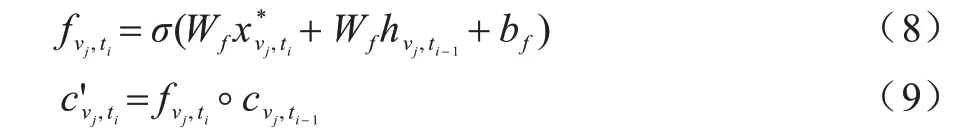
步驟2LSTM 從輸入特征中選取重要信息，用于更新狀態單元c′vj，ti：

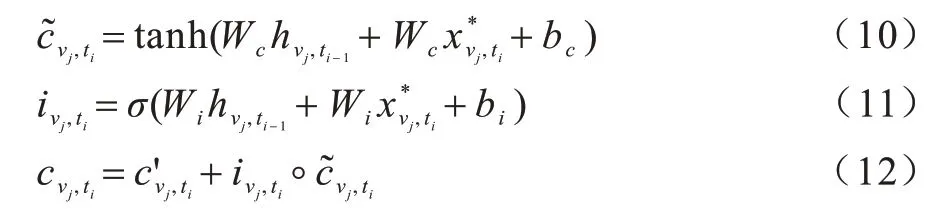
步驟3確定LSTM 輸出：

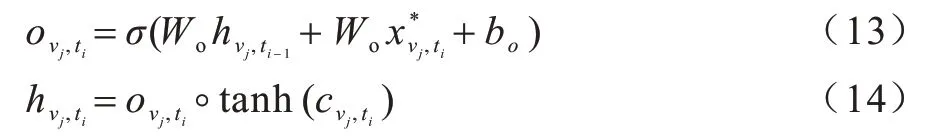
上述整個GLSTM-Block 工作流程，介紹了在時間步ti高速公路交通數據時空特征hti∈?N×d的提取過程，包括動態空間特征和時間特征。

2.5 編碼器

數據的時空特征提取過程已經在2.4節詳細介紹。為了防止每條高速道路過分依賴周邊道路信息，同時保持自身個性化的時間序列特征，本文研究獨立于GLSTM-Block，專門使用時間序列網絡LSTM 來提取原始輸入數據的時間特征，如圖3 中編碼器部分所示。LSTM 的時間序列特征提取過程如式（8）～式（14）所示，并且輸出時間特征為。最后，將LSTM 的輸出和GLSTM-Block 的輸出hST=進行相加，得到最終的時空特征

給定輸入序列x={xt1，xt2，…，xtP}，xti∈?N×d，由GLSTM-Block 和LSTM 構成的編碼器用于將輸入數據的時空 相特征轉換 為隱藏 表示，用于解碼器的時間注意力層。

2.6 解碼器

解碼器內部組成類似于模型編碼器，基于GLSTM-Block，GLSTM-Block的輸出為。不同之處在于解碼器還包含其他兩個層：一個時間注意力層和一個子任務層。時間注意力層關注歷史高速公路交通數據的時空特征對每個時間步預測值的影響［33］，子任務層用全連接層實現高速公路速度預測。

2.6.1 時間注意力

直到時間步tP+i，編碼器和解碼器輸出的時空特征和分別表示為對于示例圖節點vj，可以通過多頭自注意力機制計算時間相關性［33］。從t1到tP+i的每一時間步對時間步tP+i的影響權重通過多頭自注意力機制計算，如式（15）所示：

在時間步tP+i，時間相關性可以通過式（15）～式（19）計算得到，整個高速路網的輸出為h′′tP+i∈?N×d。

2.6.2 高速公路交通速度預測

對于高速公路交通速度預測任務，將解碼器的輸出特征直接饋送到全連接層以生成預測值：

其中：Ws∈?d×1表示全連接層的權重參數。

2.6.3 損失函數

3 實驗

3.1 基線模型和評價方法

對于高速公路交通速度預測，將本文提出的ST-ANet模型與以下基線方法進行對比：

1）HA 模型：該模型在未來預測任務中使用每天同一時間的歷史數據的平均值作為預測值［3］。

2）ARIMA 模型：該模型是一種傳統的時間序列預測方法，結合了移動平均和自回歸分量對歷史時間序列數據建模［5］。

3）SVM 模型：該模型是一種支持向量回歸技術，用于交通速度的短期預測［6］。

4）Bi-LSTM NN 模型：該模型由Bi-LSTM 網絡構成，用于對每個關鍵路徑進行建模，然后使用堆疊在一起的多個Bi-LSTM 層來合并時間序列信息［18］。

5）FI-RNNs 模型：該模型將特征注入循環神經網絡，結合時間序列數據并使用堆疊的RNN 和編碼器來學習交通數據的序列特征［19］。

6）HyperNet 模型：該模型使用LSTM 和RNN 網絡來預測交通速度，使用自動機器學習方法搜索模型超參數以執行網絡訓練［20］。

7）Multi-view CNN 模型：該模型基于傳統CNN 網絡，將歷史和實時交通數據作為模型輸入預測交通速度［21］。

8）PSPNN 基于路徑的速度預測神經網絡，由CNN和Bi-LSTM 網絡組成，用于提取歷史數據的時空特征，實現基于路徑的速度預測［24］。

9）MDL 模型：該模型是一種新穎的混合深度學習模型，用于預測車道級短期交通速度，由卷積長短期記憶（Conv-LSTM）層、卷積層和全連接層組成［26］。

10）OGCRNN 模型：該模型基于GCN 和GRU 網絡的時空神經網絡模型，用于提取路段之間交通演變的復雜時空特征以預測交通速度［30］。

11）GCN-LSTM模型：該模型基于GCN 和LSTM 網絡的融合深度模型，用于提取路段之間交通數據復雜的時空特征以預測交通速度［31］。

為評估ST-ANet 模型的預測性能，使用均方根誤差（RMSE）、平均絕對誤差（MAE）和決定系數（R2）來評估觀測值yi和預測值之間的差異。這三個評價指標的計算公式如下：

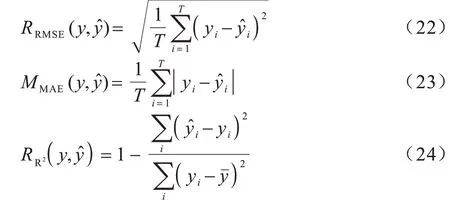
其中：T是測試集大小；yˉ表示的是觀測值的平均值。高R2和低 RMSE、MAE 值表明預測性能更精準。

3.2 模型參數

ST-ANet模型中的超參數在訓練過程中確定，即通過MAE 在測試集上選擇性能最好的模型。首先，根據經驗手動設定超參數范圍：學習率｛0.01，0.005，0.001，0.000 5｝，dropout ｛0.0，0.1，0.2，0.3，0.4，0.5｝，正則化參數 ｛0.1，0.01，0.001，0.000 1｝，衰減率｛0.99，0.95，0.90，0.85｝。對于ST-ANet 模型，發現以下設置效果最好：將 dropout 設置為0.5，衰減率設置為0.99，正則化參數設置為0.000 1，學習率設置為 0.000 5。使用基線模型時，這些設置仍然有效。所有的實驗模型通過Tensorflow框架實現，并使用Batch 大小為32 的隨機梯度下降算法（SGD）優化器訓練所有模型。在所有實驗中，模型使用了提前停止機制，即提前停止輪次和最大 epoch 分別設置為20 和50。

經過多次訓練，最終確定的模型框架參數如表1所示，其中列出了ST-ANet 模型的層數、節點數、輸出大小和相關超參數。本文提出的ST-ANet 模型和對比基線模型的具體實現代碼請參考個人GitHub主頁（https：//github.com/zouguojian/Traffic-speed-prediction/tree/main/ ST-ANet）。

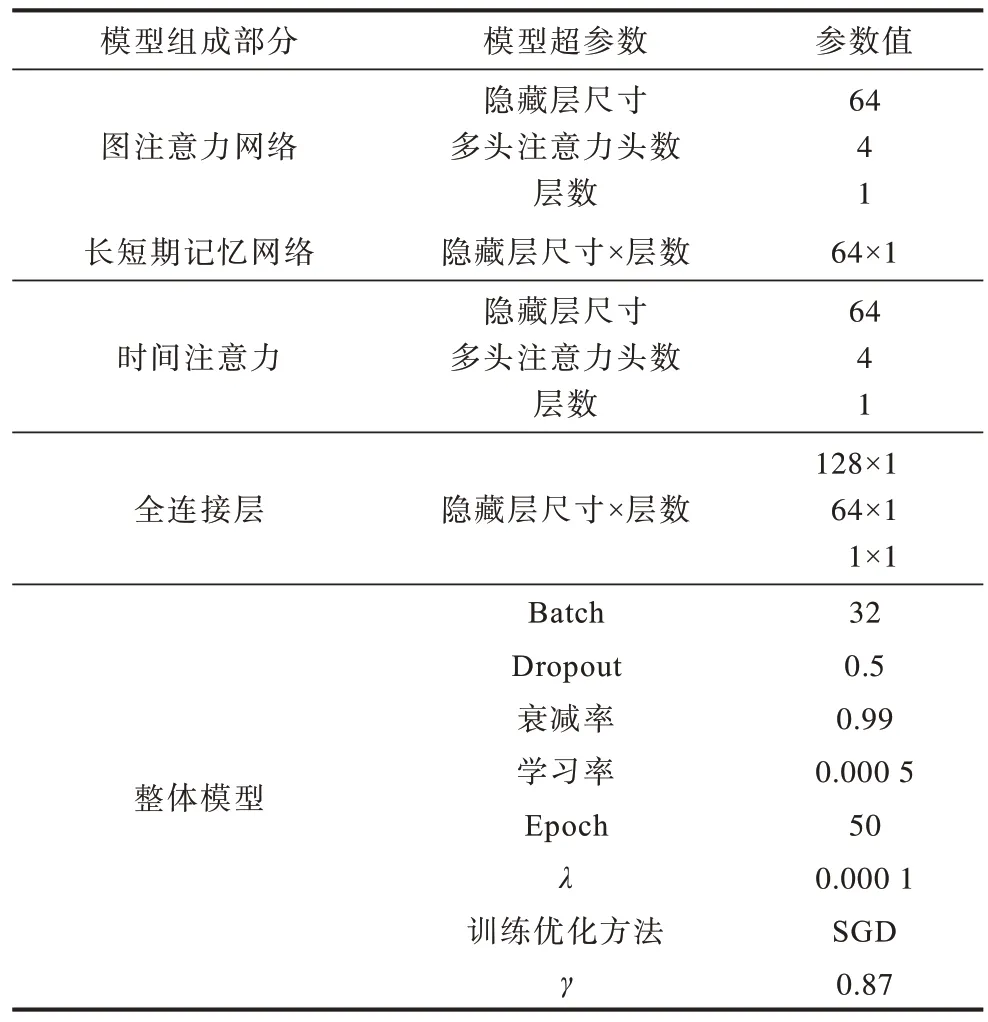
表1 模型參數 Table 1 Model parameters

3.3 不同模型表現對比

3.3.1 單步預測表現對比

交通速度單步預測任務意義顯著，也是當前的研究熱點。目前多數交通速度預測研究集中在下一時刻的單步預測，這與區域高速路網的交通運行狀況緊密相關。因此，本文繼續將下一時刻的交通速度預測作為研究目標任務，預測結果如表2 所示，其中加粗表示最優值。實驗中，使用歷史6 h 數據來預測下一小時的交通速度 ［6-1 h］。例如，上午05：00—11：00 是輸入時段，上午11：00—12：00 為預測時段。

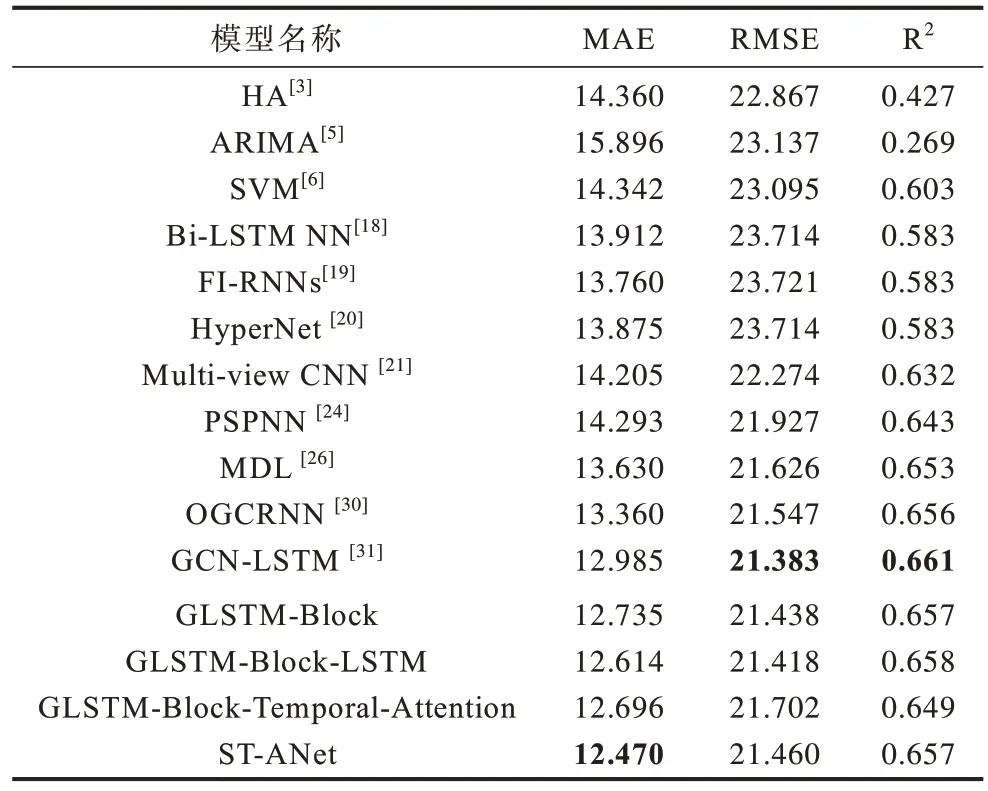
表2 不同方法的交通速度預測結果（［6-1 h］預測任務）Table 2 Traffic speed prediction results of different methods（［6-1 h］prediction task）

由表2 可以看出，HA 和ARIMA 的性能遠不如所有其他基線模型，這說明了高速公路交通速度預測的難度。統計模型最佳MAE、RMSE和R2值分別為14.360、22.867 和0.427。與統計方法相比，傳統機器學習方法和深度學習方法表現更好，因為它們更適合提取時空數據的非線性特征。因此，現有的研究正在逐漸從統計方法過渡到機器學習方法。

將基于RNN 和CNN 的基線模型分為時間依賴、空間依賴和時空依賴三大類。時間依賴模型包括Bi-LSTM NN、FI-RN Ns 和HyperNet，空間依賴模型包括Multi-view CNN，時空依賴模型包括PSPNN 和MDL。比較這些基線模型可以得出以下結論：

1）時間依賴模型的整體預測誤差低于空間依賴模型，最佳MAE 值為 13.760。實驗結果表明，時間特征顯著影響交通速度預測的精準性，體現使用基于RNN 網絡提取輸入數據時間相關性的優勢。

2）空間依賴模型的交通速度預測偏差和擬合優度優于時間依賴模型，最佳RMSE 和R2值分別為22.274和0.632。實驗結果表明，空間相關性在交通速度預測中起到了積極的作用，有效緩解了預測偏差過大和擬合優度低的問題。

3）與時間依賴模型和空間依賴模型相比，時空依賴模型顯著，提高了交通速度預測的性能。最佳MAE、RMSE 和R2值分別為13.630、21.626 和0.653。實驗結果表明，結合輸入數據的時間相關性和空間相關性兩個方面的特征，可以有效提高公路交通速度預測的準確性。

在基線模型中，基于GCN 和RNN 的時空依賴模型包括OGCRNN 和GCN-LSTM。對比OGCRNN、GCN-LSTM 和PSPNN 模型可知，OGCRNN 和GCNLSTM 的預測表現更好，對應的最優MAE、RMSE 和R2的值分別為12.985，21.383 和0.661。實驗證明GCN 解決了CNN 網絡面臨的問題，可以有效地提取非歐幾里德空間中離散道路之間交通數據的空間相關性。對比OGCRNN 和GCN-LSTM 的預測結果可知，GCN-LSTM的預測結果明顯好于OGCRNN。GCN-LSTM 的預測結果證明，LSTM 相對于GRU 更適用于時間序列特征提取。本文研究繼續考慮非歐式空間中交通數據的空間離散分布問題，將GCN 延伸到GAT 模型：

1）使用基于空間注意力的GAT 提取高速公路網絡動態空間相關性。

2）與GCN-LSTM 模型類似，使用LSTM 作為時間特征提取器獲取輸入數據的時間相關性。

3）使用時間注意力機制計算歷史輸入數據與當前預測值之間的相關性，以完成交通速度預測。通過將本文提出的ST-ANet模型與基線模型對比，ST-ANet模型的預測性能得到較大的提升。與最優基線模型GCNLSTM 相比，模型的預測誤差減小了4.0%。

3.3.2 消融實驗

使用以下模型進行消融實驗并對結果進行分析：

1）GLSTM-Block。與GCN-LSTM 模型相比，GLSTM-Block 模型也是使用LSTM 作為時間特征提取器；不同之處是，GLSTM-Block 使用基于空間注意力機制的GAT 提取輸入數據的動態空間相關性，而GCN-LSTM 是依托于GCN 提取靜態空間相關性的。與GCN-LSTM 相比，GLSTM-Block 取得了更好的表現，MAE 降低了1.9%。實驗結果證明：一方面，相比于GCN，GAT 考慮到了空間特征的動態變化，這對高速公路網路的空間相關性特征提取效果要更加顯著；另一方面，考慮路段之間的動態影響可以有效緩解預測能力不足的問題。

2）GLSTM-Block-LSTM。高速路網中的每條公路不僅受周邊公路影響，更受到自身速度的影響。相比于GLSTM-Block，GLSTM-Block-LSTM模型在Encoder部分添加獨立于GLSTM-Block 模塊用于提取每條公路速度時間序列特征的LSTM 網絡，目的是為了保留每個路段自身的時序特征而不受周邊路段的影響。與GLSTM-Block 預測結果相比，GLSTM-Block-LSTM 模型的預測表現得到提升，并且MAE、RMSE 和 R2這3 個評判指標測量值都得到更新，分別改善了1.0%、0.1%和0.2%。通過實驗可知，道路的自身固有時序特征對道路交通速度預測任務影響較大。因此，在高速公路速度預測任務中，不僅需要考慮高速路網時空特征問題，而且還需要保留每一條道路固有的時間序列特征。

3）GLSTM-Block-Temporal-Attention。高速公路未來時間段的交通速度預測值會受到過去一段時間的交通速度影響。為此，本文提出基于時間注意力的GLSTM-Block-Temporal-Attention 模型。與GLSTM-Block相比，GLSTM-Block-Temporal-Attention在預測階段會考慮當前預測與歷史輸入數據之間的相關性。通過與GLSTM-Block實驗對比可知，添加時間注意力后的模型預測表現整體誤差減小，MAE值降低了0.3%。誤差降低的可能原因是，模型更加關注時間維度歷史輸入數據與預測值之間的相關性。這也反映了時間注意力機制在交通預測任務中的積極作用，可作為交通速度預測模型的重要組件之一。

4）ST-ANet。通過對GLSTM-Block，GLSTM-Block-LSTM和GLSTM-Block-Temporal-Attention 模型預測結果的分析，可總結得到基于空間注意力的GAT、LSTM和時間注意力機制對交通速度的預測具有不同程度的影響。為了綜合三者的優勢，本文在GLSTM-Block 模型中添加用于獨立提取高速公路每條道路交通速度時間序列特征的LSTM，以及用于計算歷史輸入數據與當前預測值相關性的時間注意力機制，最終得到ST-ANet模型。與最優基線模型GCN-LSTM 相比，ST-ANet 的預測誤差得到了大幅改善，MAE 減小了 4.0%。

3.3.3 長期預測表現對比

目前的交通速度預測研究主要集中在短期預測，不足以滿足實際應用場景的需要。高速公路交通速度的長期預測對于預測模型來說是一項具有挑戰性的任務，它關系到未來一段時間公路交通的精確管控。對于表2 中的結果，已經證明了ST-ANet在短期預測任務中的有效性，并分析了模型各部分的貢獻。為了驗證ST-ANet在長期預測任務中的優勢，表3 分別顯示了基線模型和ST-ANet 模型在未來2 h 和3 h 的交通速度預測任務中的表現。由于基線模型的局限性，本階段從表2 中選擇性能好，并適用于長期預測的基線模型進行實驗對比。對于［6-2 h］交通速度預測任務，使用6 h的歷史交通數據作為輸入，預測未來2 h 的交通速度，例如05：00—11：00 為輸入時段，11：00—13：00 為預測時段。對于［6-3 h］交通速度預測任務，使用6 h 的歷史交通數據作為輸入，預測未來3 h 的交通速度，例如05：00—11：00為輸入時段，11：00—14：00為預測時段。

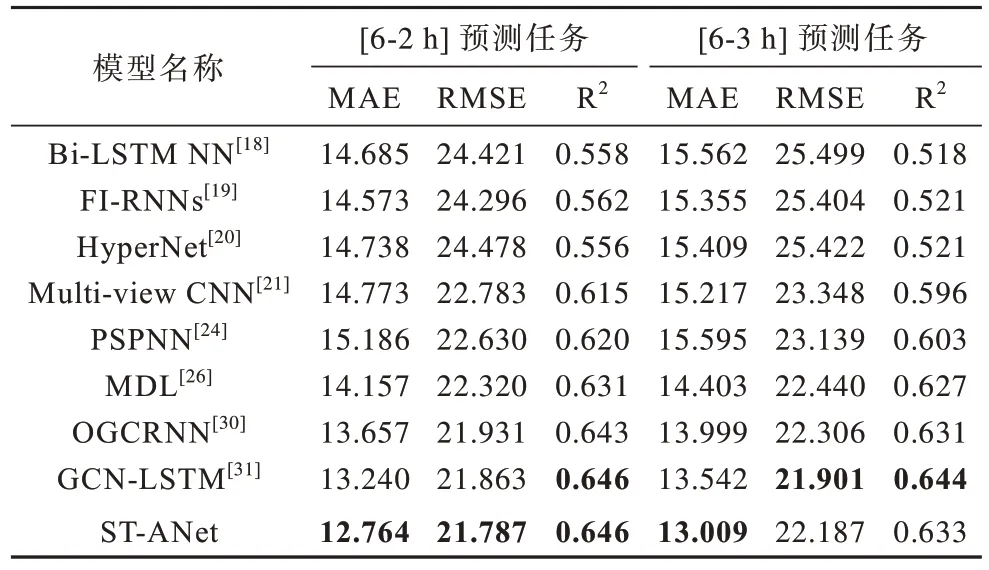
表3 不同方法的交通速度預測結果（［6-2 h］和［6-3 h］預測任務）Table 3 Traffic speed prediction results of different methods（［6-2 h］and ［6-3 h］prediction tasks）

為了更清楚地對不同模型的預測結果進行對比，對每個模型的預測誤差、偏差和擬合優度進行可視化，如圖7 所示。結合圖7 和表3 可知，與用于長期預測任務的基線模型相比，ST-ANet表現最佳。對于交通預測任務［6-2 h］，與最優基線模型GCN-LSTM 相比，MAE改進為3.6%，RMSE 改進為0.3%。對于交通預測任務［6-3 h］，與基線模型相比，MAE 改進為 3.9%。此外，如圖7 所示，與基線模型相比，ST-ANet 的誤差隨著時間步數的增加變動幅度較小，且誤差小于所有基線模型。由于ST-ANet 的預測結果優勢顯著，因此具有巨大的應用前景。值得注意的是，ST-ANet 的預測偏差和擬合優度要略低于GCN-LSTM，原因可能是GCN對于降低模型偏差和提高擬合優度方面的作用要好于GAT，而GAT 對于降低模型的誤差方面起著不可或缺的作用。ST-ANet 和GCN-LSTM 模型的特性給未來的交通路網交通速度預測帶來了新的啟發，深度結合GCN 和GAT 的優勢將是未來研究的一個重要方向。

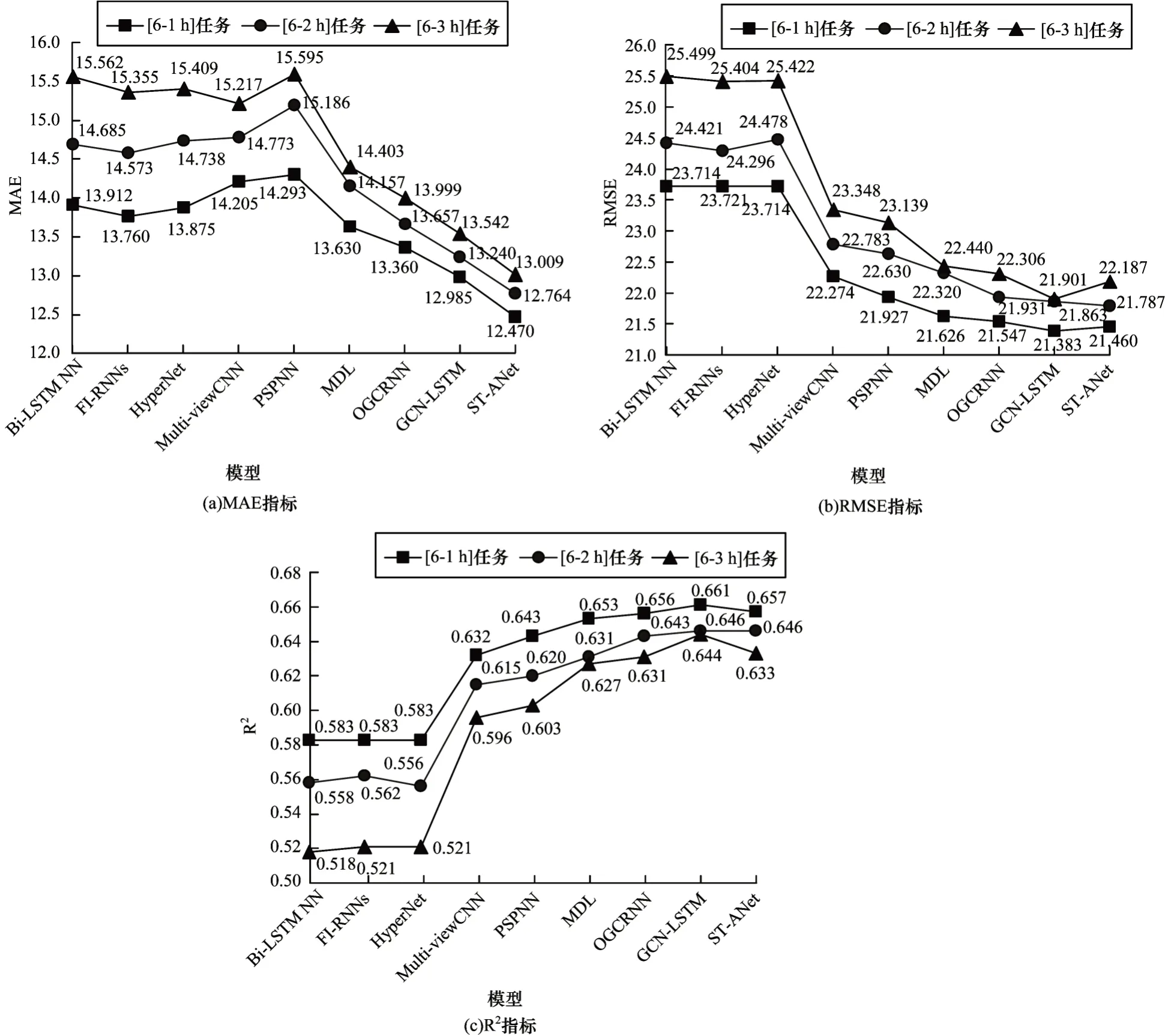
圖7 長期交通速度預測能力Fig.7 Long-term traffic speed prediction ability

4 結束語

本文基于時空注意力網絡，提出一種面向動態高速路網的交通速度預測模型ST-ANet。為評估模型性能，對真實世界的高速公路交通數據進行多次實驗。對于高速公路交通速度短時預測，在相同的測試集上，ST-ANet比基線方法具有更準確的交通速度預測性能。對比最優基線模型GCN-LSTM，ST-ANet模型對于未來1 h 預測誤差MAE降低4.0%。此外，對于長期預測任務，ST-ANet的預測誤差、偏差和擬合優度的變化范圍較小。對比次優基線模型GCN-LSTM，ST-ANet模型對于未來2 h和3 h內高速路網交通速度的預測誤差MAE 分別降低3.6%和3.9%。后續將在ST-ANet模型中添加GCN 網絡，進一步減小模型的預測誤差并提高模型的擬合優度，同時并探索用于未來預測的高性能模型。