無裝配條件下角接觸球軸承旋轉精度測量方法研究＊

季曄 鄭昊天 王東峰 馬新忠

（①洛陽理工學院智能制造學院，河南 洛陽 471023；②洛陽軸承研究所有限公司，河南 洛陽 471039）

角接觸球軸承（ACBB）在機床主軸中廣泛應用，其旋轉精度直接決定機床加工精度。高檔精密機床中所使用的ACBB精度為P2或P4級，套圈采用超精密加工，但成品合格率仍然較低，往往需要多次合套選配。合套和拆套過程不僅耗費工時，還可能引起精度下降，甚至喪失。因此，開展無裝配條件下的成品旋轉精度研究非常必要。

高精度機床市場需求旺盛，軸承精度直接決定機床加工精度，其旋轉精度引起了國內外學者廣泛關注。王曉明等[1]根據角接觸球軸承的幾何和運動關系，建立了考慮外圈溝道圓度誤差的軸承外圈徑向跳動、軸向跳動數值仿真模型，分析了外圈溝道圓度誤差階次、圓度誤差幅值和鋼球個數對外圈旋轉精度的影響，并進行了理論驗證。魏建波等[2]建立了多種基于Copula函數數學分析模型，分別研究了兩組不同分布狀態的特征變量與軸承徑向跳動的相關系數與條件概率。陳月等[3-4]針對機器人用四點接觸球軸承旋轉精度難以預測和控制的問題，提出了同時考慮軸承內圈溝道和外圈溝道圓度誤差的軸承旋轉精度數值計算方法。余永健等[5-6]針對圓柱滾子軸承旋轉精度，提出了軸承外圈徑向跳動數值計算方法，并對外圈滾道形狀誤差進行了試驗研究，分析了外圈滾道圓度誤差幅值、諧波階次對軸承旋轉精度的影響規律。崔立等[7]建立了ACBB套圈溝道輪廓圓度誤差模型，考慮軸承圓度誤差、諧波次數等溝道參數將軸承組與主軸裝配，建立了高速電主軸動力學仿真模型，分析了軸承溝道參數及預緊對主軸旋轉精度的影響以及軸承公差等級與溝道參數的匹配。周元坤等[8]根據圓柱滾子軸承各零件間的幾何關系，推導出軸承幾何協調方程，將幾何協調方程與載荷平衡方程聯立進行迭代求解，建立基于載荷平衡與幾何協調共同作用下軸承旋轉精度的數學模型，研究了內圈滾道圓度誤差諧波幅值、諧波階次對軸承內圈徑向跳動的影響。

目前判斷滾動軸承旋轉精度是否滿足要求，需要合套后在專用儀器上檢測，現有的研究大多是旋轉精度預測及分析某些參數對旋轉精度的影響。本文分析了ACBB工作狀態下的幾何學關系，建立了基于套圈精度要素的ACBB旋轉精度數學模型，提出了不合套條件下的旋轉精度測量方法，分析了套圈精度要素對成品ACBB的影響。通過ACBB旋轉精度檢測，證明了數學模型的準確性，實現了無合套條件下成品軸承旋轉精度檢測。

1 ACBB旋轉精度測量原理

ACBB工作狀態如圖1所示，根據旋轉精度檢測方法[9]，將外圈基準端面放置于一水平面，內圈在重力和預載荷作用下下移，球與內圈和外圈溝道接觸，形成接觸角α。測頭放置于內圈內徑面與溝底水平的A'處（測量點1）。內圈旋轉，A'處表針擺動量即為旋轉精度。

2 ACBB幾何學關系分析

ACBB工作狀態可以建立如圖1所示的幾何關系。O′O為軸承外圈確定的中心線，O為ACBB外圈的幾何中心，O′是內圈溝底處水平中心線與外圈豎直中心線交點，O′O右側虛線為內圈中心線；點m為內圈溝道圓心，點n為外圈溝道圓心；Oi為球與內圈接觸點，Oe為球與外圈接觸點；OKi為內圈溝底，OKe為外圈溝底；ODw為球的中心，Of為球豎直中心線與外圈水平中心線交點；OiOe與O′O交點為O′′，與內圈內徑的交點為A′′，O′與m的連線與內徑交點為A′，建立笛卡爾坐標系如圖1所示。

圖1 ACBB工作狀態

不失一般性，在xoy面內，如圖2所示，假設內圈和外圈第1個檢測點均與x軸重合，內圈其余點相對第1個檢測點的位置角用θi表示，外圈其余點相對第1個檢測點的位置角用θe表示。內圈轉速為ωi，θ表示相對于外圈第1個檢測點即A′處表針某時刻的位置角。

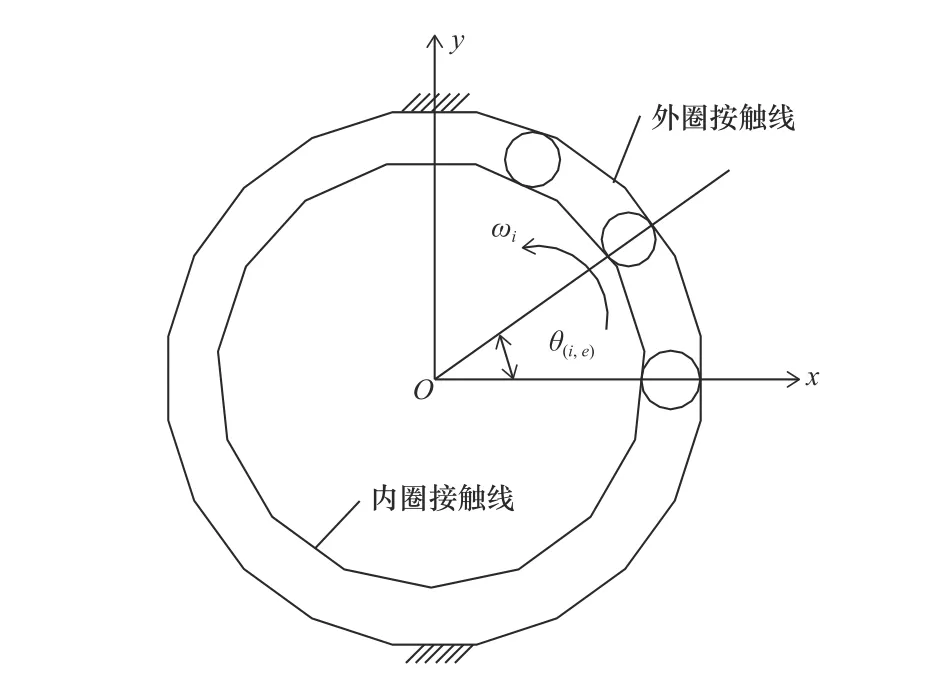
圖2 套圈初始位置

α為球與內、外圈接觸點的作用線與垂直于軸承軸線的平面夾角；旋轉精度用徑向跳動值Kia衡量，表示內圈內孔表面某測量位置相對外圈一固定點間的最大與最小徑向距離之差。OO′′表示線段OO′′長度，其余同理；公式中變量下標表示圖2中套圈或成品在位置角為θi,e或θ時的瞬時值。根據三角形關系，α滿足[10]

圖1中，△O′O′′m與△A′A′′m相似，且∠O′′O′m和∠A′′A′m均為直角。以外圈外徑為基準，存在

根據幾何關系，OO′表示的軸向游隙(θ)，滿足

施加預緊力后，內圈旋轉，O′A′的變化量表示ACBB內圈徑向跳動值Kia（測量點1），表示為

對于第j個球對應的O"點的坐標[0;0;zO”(θ)]T滿足

式中：k1、k2為鏡頭徑向畸變參數；p1、p2為切向畸變參數。采用主流的相機標定方法[12],可獲得相機的內外參數及鏡頭畸變參數。

其中：di(θi)為 θi位置處的內圈溝底直徑；de(θe)為 θe位置處的外圈溝底直徑。

O′O′′長度為點O′′與點O′的z軸坐標值之差，即

在△O′O′′m中，存在

A′OKi(θ)表示內圈壁厚，表示為

根據幾何關系，存在

其中：d(θi)為 θi位置處的內徑。

3 ACBB旋轉精度測量原理

考慮計算精度和檢測效率，在內圈和外圈非基準端面打9個均勻分布的標記點，測量標記點處精度參數，根據零件設計參數測量結果求解成品精度，步驟如圖3所示。

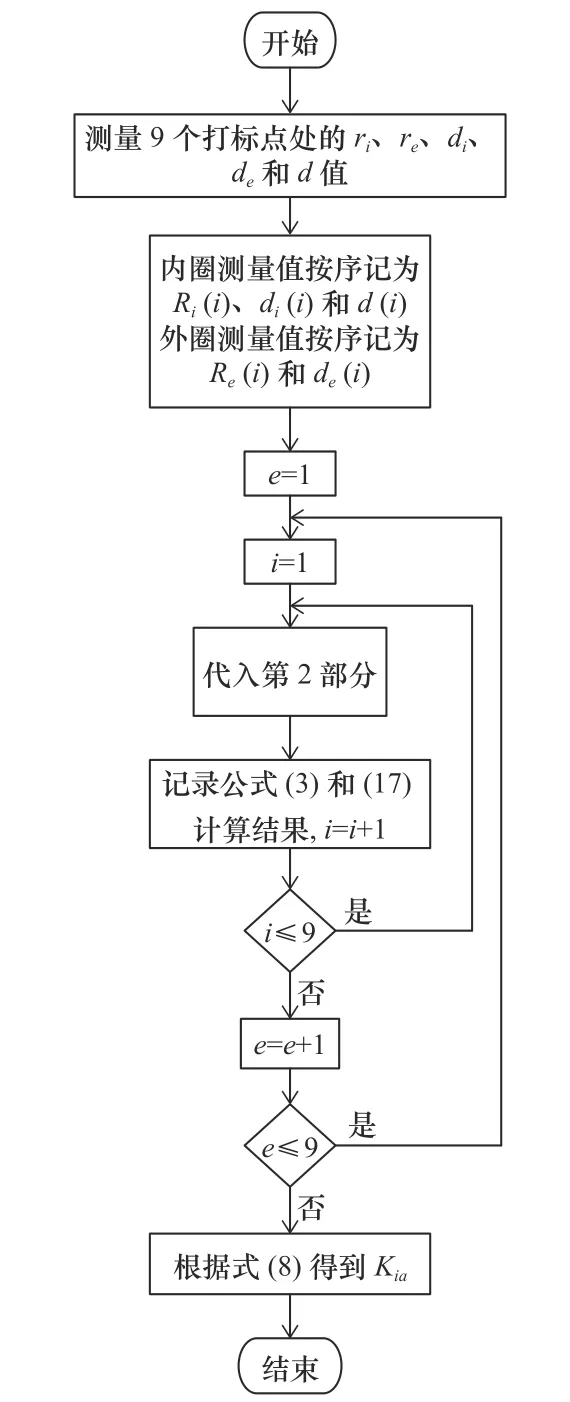
圖3 ACBB旋轉精度計算流程

4 算例

4.1 套圈精度檢測和成品精度分析

以7006-ACBB套圈為例，在9個檢測點處利用表面形貌測量儀、圓度測量儀，長度測量儀和旋轉精度測量儀分別對套圈和成品進行檢測和計算結果驗證。

（1）套圈精度檢測

用長度測量儀完成內徑參數測量，9個點檢測結果如表1所示。

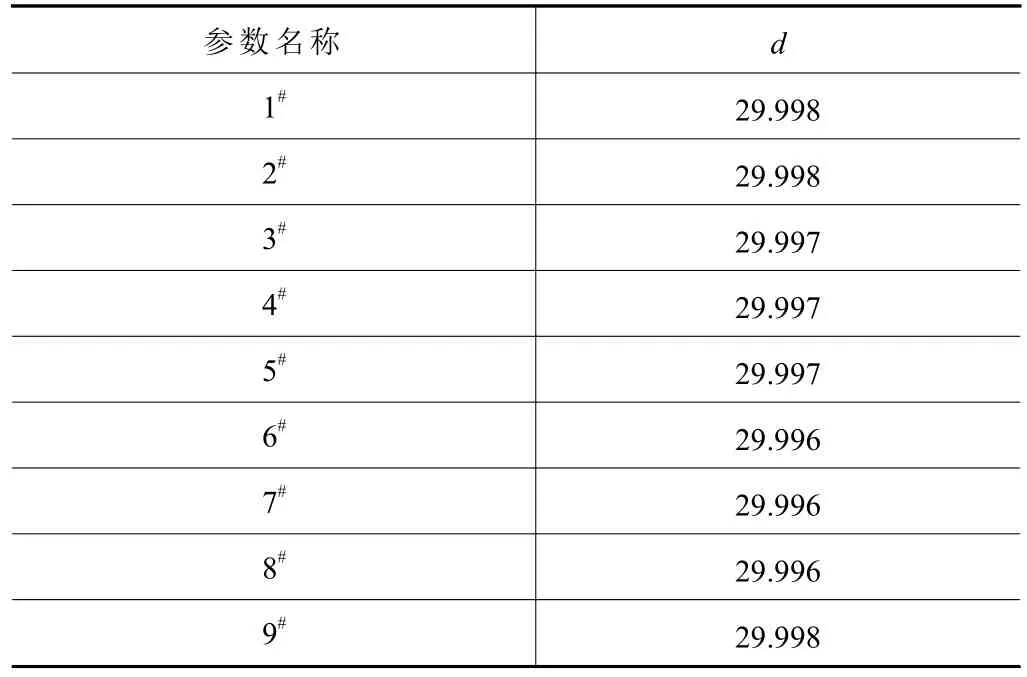
表1 內徑測量結果

溝底直徑用圓度測量儀檢測，9個標記點檢測結果如表2所示。

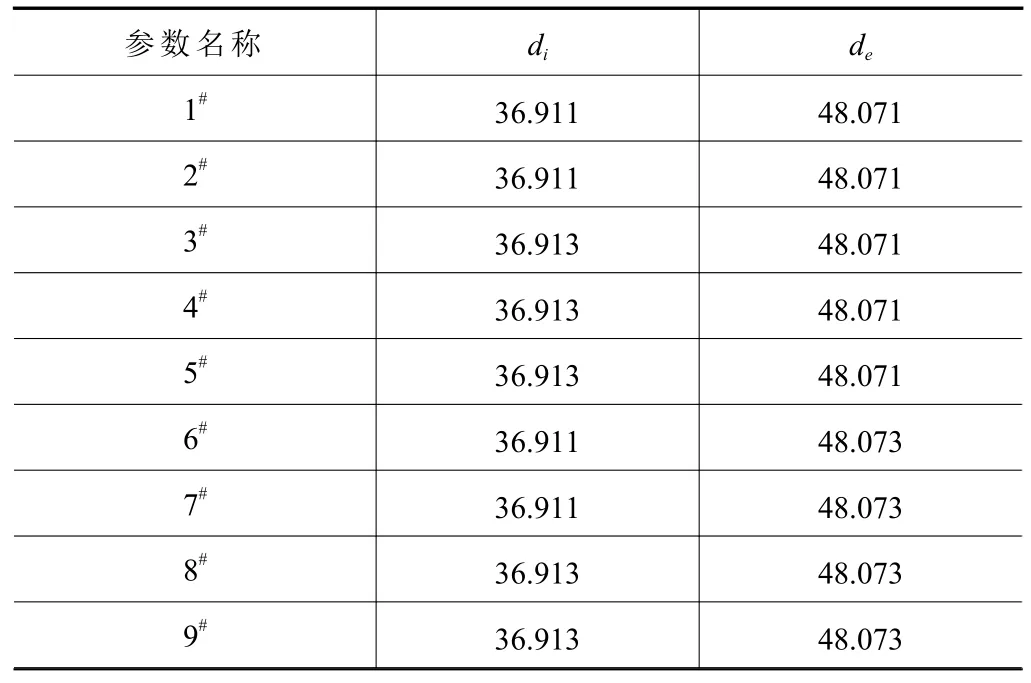
表2 溝底直徑檢測結果

套圈的溝曲率半徑采用表面形貌測量儀檢測，檢測結果如表3所示。

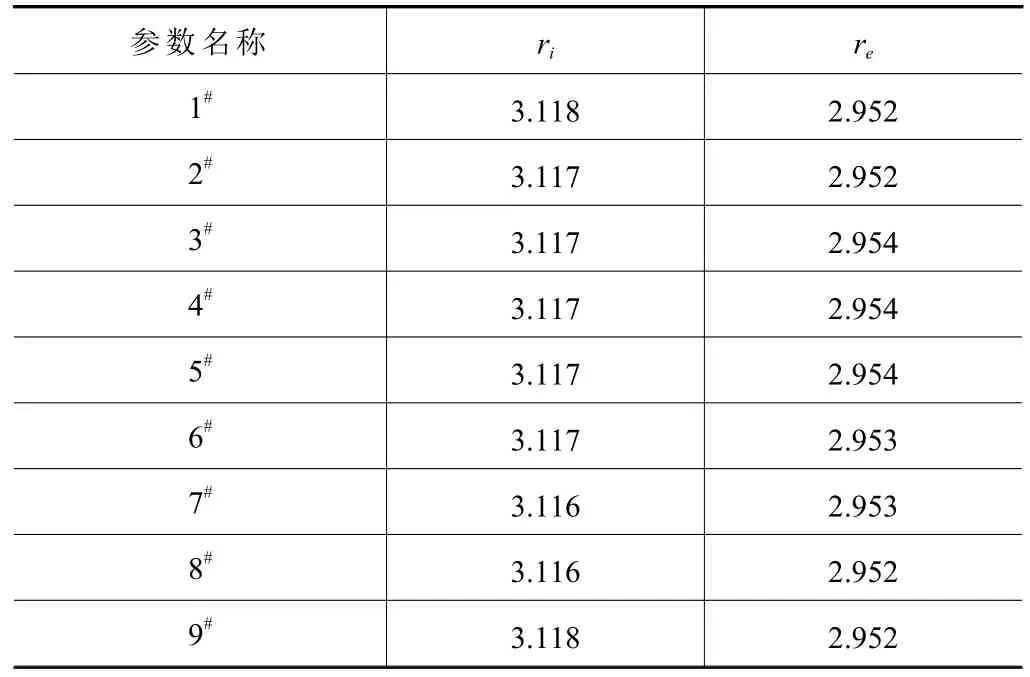
表3 溝曲率半徑檢測結果

（2）成品精度分析

根據圖3計算得到α最大值為17.98 °，最小值為17.17 °；Kia等于0.002 mm。利用旋轉精度測量儀（圖4）檢測無潤滑、不帶保持架的成品7006-ACBB徑向跳動為0.002 mm，與計算結果一致。

圖4 旋轉精度測量儀

4.2 ACBB旋轉精度分析

（1）ACBB旋轉精度變化趨勢預測

ACBB旋轉精度變化規律由套圈精度參數分布規律決定，影響轉子系統周期性變化規律。套圈精度測量參數為離散數據，分別采用指數擬合、多項式擬合、傅里葉擬合和線性擬合描述輪廓曲線，方程如式（18）～（21）所示。

其中：θ為套圈輪廓曲線某一點相對第1個測量點的位置角；其余字母為擬合曲線系數。

將內圈精度參數ri、di、d和外圈精度參數re、de檢測的9個點用于擬合，每個參數可以得到4種不同的輪廓曲線。輪廓曲線方程代入第二部分，求解流程如圖5所示。

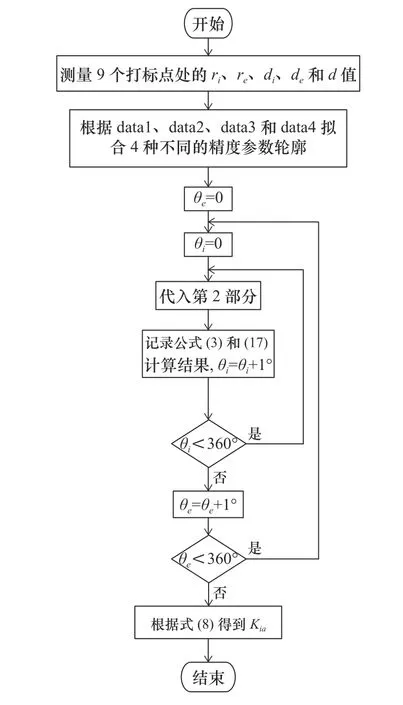
圖5 不同擬合輪廓的ACBB旋轉精度計算流程

運用data1、data2、data3和data4擬合曲線得到的套圈輪廓計算得到的Kia分別為0.006 4 mm、0.003 2 mm、0.000 7 mm和0.001 8 mm，旋轉精度變化趨勢如圖6所示

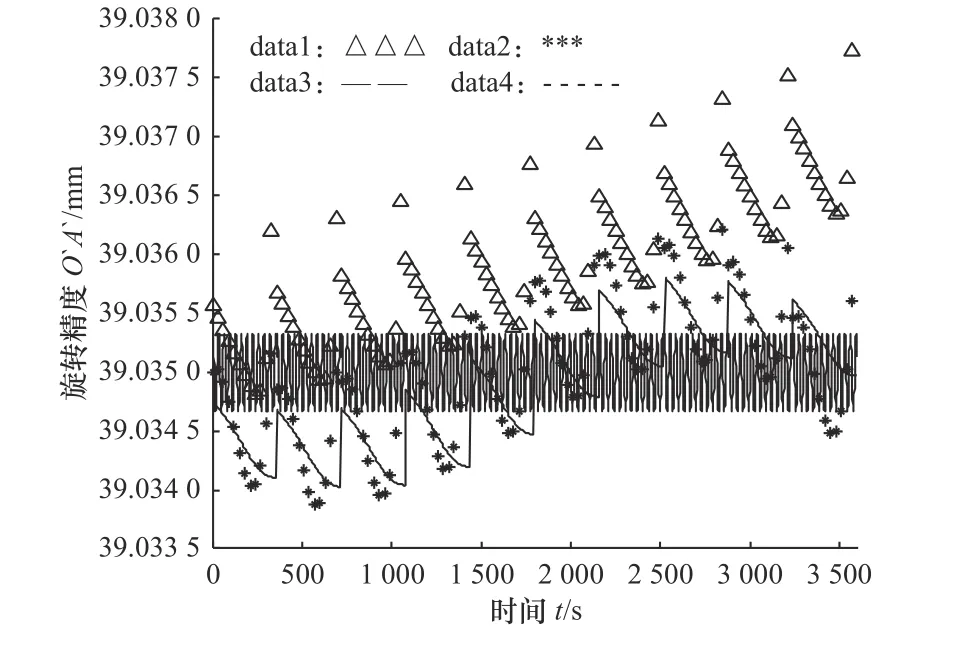
圖6 不同擬合輪廓旋轉精度變化趨勢

與檢測結果對比發現，data1變化明顯偏大，data2略大且變化趨勢與檢測結果有差異，data3明顯偏小，data4與檢測結果最為接近。因此，采用data4得到的擬合輪廓與真實輪廓接近。

（2）溝曲率半徑對ACBB旋轉精度的影響

ri和re按data4的擬合輪廓，其余參數取9次檢測的平均值，計算得到的Kia為2.84×10-14mm，說明溝曲率半徑對旋轉精度影響很小，非敏感因素。

（3）溝底直徑對旋轉精度的影響

di和de按data4的擬合輪廓，其余參數取9次檢測的平均值，計算得到的Kia為0.001 2 mm，旋轉精度變化規律如圖7所示。顯然，di和de為敏感因素，其精度直接決定ACBB旋轉精度。

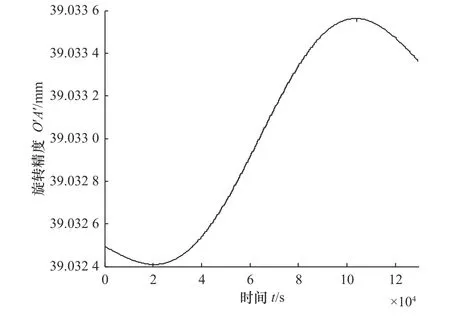
圖7 di和de與旋轉精度關系

（4）內徑對旋轉精度的影響

內徑d按data4的擬合輪廓，其余參數取9次檢測的平均值，計算得到的Kia為0.000 7 mm，說明d會影響旋轉精度。

5 結語

（1）通過對角接觸球軸承工作狀態下的幾何關系分析，建立了套圈精度參數與成品軸承的解析模型，可以充分研究內徑、溝曲率半徑和溝底直徑等因素對角接觸球軸承旋轉精度的綜合影響。

（2）本文所采用的計算方法可以在僅檢測套圈設計參數的條件下，得出成品旋轉精度，避免因合套和拆套引起的精度喪失，有助于提高成品合格率。

（3）通過對內徑、溝底直徑與旋轉精度關系的分析，結合套圈設計精度參數，為了保證ACBB具有良好的旋轉精度，需嚴格控制內徑變動量和壁厚差。