聚脲彈性體力學性能與本構關系研究進展1)

龔臣成 陳艷 戴蘭宏

(中國科學院力學研究所非線性力學國家重點實驗室,北京 100190)

(中國科學院大學工程科學學院,北京 100049)

引言

近十幾年來,聚脲(polyurea)作為一種新型聚合物彈性體材料,憑借其高強度、高韌性等優異的力學性能以及與各類工程材料良好的黏接性,在防爆抗沖擊領域得到了廣泛的關注與應用[1-9].由于合成聚脲的反應物種類繁多[10-12],且反應物比例對聚脲性能具有顯著影響[11-13],使得聚脲的性能呈現很大的可調節性.此外,聚脲還具有良好的耐磨、耐腐蝕、防水、防輻射和阻燃等性質[14-18],這些特點使得其成為一類適用于多種工程應用場景的多功能材料.

聚脲優異的性能與其微結構密不可分.聚脲是一類主鏈上含有重復脲基(-NH-CO-NH-)鏈段的聚合物,一般通過異氰酸酯組分(含異氰酸根-N=C=O)與氨基組分(含氨基-NH2)的聚合反應形成[15,19-21].聚脲的共聚反應原理圖如圖1 所示,其中R 表示一種芳香官能團,R'表示一種芳香族或脂肪族長鏈官能團.其中,R'官能團部分非常柔順,一般呈無規則蜷曲狀態,被稱為柔性鏈段(或軟段);而脲基與R 官能團組成的基團比較剛硬,不易改變構象,通常被稱為剛性鏈段(或硬段)[16].因此,聚脲是一種由軟段和硬段交替連接而成的(AB)n型嵌段共聚物.由于聚脲軟硬段熱力學上不相容,且硬段中脲基的極性使得其傾向于結合在一起,促進硬段間氫鍵形成,從而在聚脲內形成納米級的硬段聚集區域,稱為硬疇或硬相.硬疇的玻璃化轉變溫度要高于常溫,在常溫下呈玻璃態[22].而軟段和少量離散的硬段組成包裹硬疇的基體,稱為軟基或軟相,其玻璃化轉變溫度低于常溫,常溫下呈橡膠態[22].聚脲這種硬疇分散于軟基中的結構被稱為微相分離結構.圖2 是通過原子力顯微鏡獲得的聚脲微相分離結構的示例圖[19],圖中明亮條帶是硬疇,隨機分布在連續相軟基(暗區)中.硬疇在聚脲中起著兩種主要作用,一是作為增強體提高結構的剛度,二是通過氫鍵將大分子鏈交聯在一起.由于這種氫鍵交聯不同于共價鍵交聯,聚脲呈現出一定的熱塑性,是一種具有微相分離結構的熱塑性彈性體聚合物或納米級彈性體基復合材料[23].

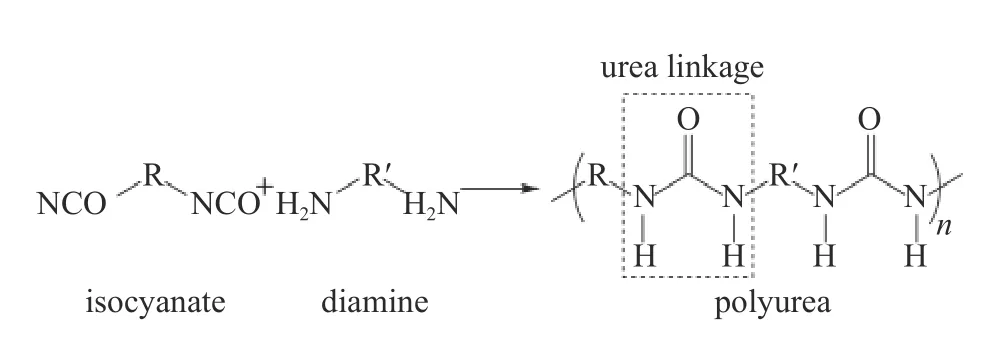
圖1 聚脲共聚反應原理圖Fig.1 Schematic of the copolymerization reaction resulting in the formation of polyurea

圖2 聚脲微相分離結構AFM 圖像[19]Fig.2 AFM image of the microphase-segregated structure in polyurea[19]

聚脲獨特的微結構賦予了其優異的力學性能,同時也導致了其復雜的靜動態力學行為.已有的研究表明,聚脲應力?應變響應具有非線性大變形的特點,且呈現顯著的溫度、應變率及壓力敏感性,循環加載下表現出類似于炭黑填充橡膠的Mullins 效應[24],即循環加載軟化現象.

聚脲的靜動態力學性能研究是認識其防爆抗沖擊機理的基礎,從理論及模型上定量描述材料的力學行為是有效預測材料變形失效行為及優化材料性能的關鍵.因此,本文主要從實驗和理論兩方面分別對聚脲彈性體材料的靜動態力學性能與本構模型研究現狀進行綜述: 首先,對聚脲力學性能實驗研究現狀進行概述.其次,根據建模方法,對國內外學者所建立的各類聚脲本構模型進行簡要介紹和評述.最后,對后續聚脲力學性能和本構關系理論的研究工作提出相關建議和展望.

1 聚脲力學性能

聚脲在防爆及抗沖擊領域顯示出的重要應用價值使得研究人員開始關注聚脲的力學性能研究.深入認識聚脲在不同載荷下的力學行為對于厘清其防爆抗沖擊機理至關重要.對聚脲力學性能的研究主要可以分為兩部分: 小變形條件下的線性黏彈性行為和大變形下的非線性黏彈性行為.

1.1 小變形線性黏彈性

小變形情況下的線性黏彈性反映了材料微結構不隨變形改變情形下的性質,是對材料動態力學性能的初步認識.動態力學分析DMA、小變形松弛實驗、超聲實驗等作為常用的材料線性黏彈性分析的手段[25],被用于聚脲小變形線性黏彈性性能的研究中.

Knauss[26]較早地針對聚脲進行了不同溫度(?53 °C～ 0 °C)下的小變形松弛實驗,并基于時溫等效原理將不同溫度下的數據平移疊加得到材料在參考溫度為0 °C 下的10?10～ 104s 時間范圍內的松弛模量(如圖3),相應的時溫轉換因子與WLF 方程[27]預測較為吻合,其數據也被用于下文2.2.1 中Amirkhizi-Nemat-Nasser 模型[15]的參數擬合.Knauss 的實驗表明,通過時溫等效的方法將聚脲不同溫度下較窄時間范圍的黏彈性力學數據擴展到參考溫度下更寬時間范圍是可行的.Zhao 等[28]之后用同樣方式獲得了聚脲的松弛模量主曲線,并將數據用于線性黏彈性模型,模擬了聚脲小變形條件、不同溫度下的霍普金森桿壓縮實驗,且與實驗結果吻合較好.

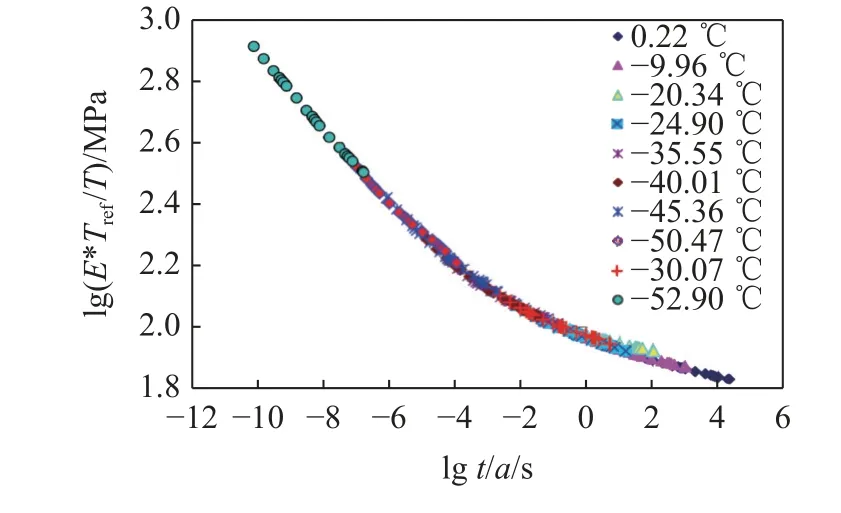
圖3 聚脲時溫等效得到的松弛主曲線[26]Fig.3 Master relaxation curve of polyurea obtained through Time-Temperature superposition[26]

Chevellard 等[29]對聚脲進行了不同溫度(?58 °C～40 °C)下的Arcan 剪切松弛實驗、單軸壓縮松弛實驗以及不同壓強(62～ 850 MPa)下的側限壓縮松弛實驗,得到了聚脲的剪切松弛模量主曲線和體積松弛模量主曲線,并研究了溫度、壓強對材料線性黏彈性的影響.實驗發現在松弛時間范圍內,松弛模量由1 GPa 降低到10 MPa 水平,而體積模量僅由2.5 GPa 降到1.5 GPa,即體積松弛模量的時間相關性遠弱于剪切松弛模量.此外,當聚脲受到壓強作用時,壓強越大,材料表現出松弛模量越大或松弛時間更長;類似于時溫轉換因子,他們得到了相應的時壓轉換因子,表現為隨壓強增大而增大,但增速減小,即壓強對松弛的影響隨壓強增大逐漸飽和.

Qiao 等[30]結合DMA 和超聲實驗研究了聚脲不同溫度、不同頻率下的線性黏彈性性能.DMA實驗測量了聚脲在?80 °C～ 70 °C、5 組頻率下的儲能模量和損耗模量,并基于時溫等效原理獲得了參考溫度為1 °C 下的主曲線及松弛譜,并通過時溫轉換因子數值求得了聚脲α松弛的表觀激活能隨溫度的關系: 隨溫度降低,激活能增大.他們進一步通過超聲實驗測量了聚脲的縱波和剪切波在溫度范圍為?60 °C～ 30 °C、頻率范圍為0.5～ 2 MHz 的波速及衰減情況,并通過線性黏彈性理論公式將數據轉換為儲能模量和損耗模量,與DMA 數據進行對比(如圖4).超聲實驗轉換的儲能模量與DMA 數據吻合,但損耗模量比DMA 獲得的數據大,他們認為這是硬疇在高頻下共振的結果.

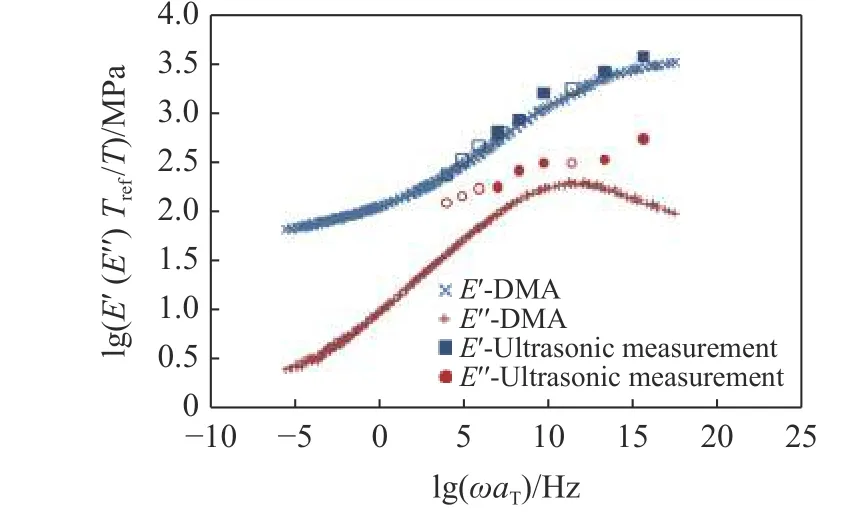
圖4 聚脲DMA 動態模量主曲線與超聲實驗對比[30]Fig.4 Comparison of the master dynamic modulus curves from the DMA tests and ultrasonic measurements on polyurea[30]

Nantasetphong 等[31]通過改造的霍普金森壓桿裝置研究了聚脲在kHz 頻率水平的小變形線性黏彈性性能,填補了DMA 實驗低頻10?2～ 102Hz 和超聲實驗高頻(20 kHz～ 200 MHz)間的空隙.實驗借助小球撞擊壓桿產生kHz 頻率水平的小應力波,通過記錄入射桿和透射桿中的信號得到材料的波速、信號衰減信息,并通過線性黏彈性理論轉化為儲能模量和損耗模量數據.進一步將不同溫度(?50 °C～50 °C)的數據通過時溫等效得到參考溫度下的主曲線.與通過DMA 實驗和超聲實驗得到的數據比較發現,3 種實驗得到的儲能模量相當,但對于損耗模量,超聲實驗、小球沖擊實驗和DMA 實驗的數值依次降低,即不同頻率范圍測試手段獲得的數據通過時溫等效原理得到的主曲線不重合,這表明聚脲不是一種理想的熱流變簡單材料或不完全符合時溫等效原理.

通過發展不同溫度、不同頻率范圍的線性黏彈性測試手段,結合時溫、時壓等效原理等理論,研究人員對聚脲材料的小變形線性黏彈性有了一定的認識.借助于這些測試手段,研究人員進一步研究了軟硬段長度、種類、化學計量比、退火溫度等對聚脲黏彈性的影響.

Das 等[32]通過DMA 研究了不同軟段長度和不同硬段種類(六亞甲基二異氰酸酯HDI、1,4-環己烷二異氰酸酯CHDI 和對苯二異氰酸酯pPDI)對非擴鏈聚脲線性黏彈性力學性能的影響.實驗表明: 增加軟段長度,3 種聚脲的低溫(?130 °C～ ?100 °C,玻璃化轉變溫度以下)儲能模量均增大(低溫下軟段結晶度增大),而橡膠態平臺模量均減小,橡膠平臺溫度范圍變窄;由于軟段長度增大導致軟段結晶度增大,損耗因子在玻璃化轉變區形成肩峰;對于不同的硬段(包括脂肪族和芳香族),由于其性質、對稱性和剛度的不同,也對聚脲橡膠平臺溫度范圍有很大影響,如硬段含環己烷的CHDI 聚脲和硬段含苯環的pPDI 聚脲的上軟化點溫度遠大于硬段只含甲基的HDI 聚脲.

呂平等[33-35]針對擴鏈劑擴鏈的聚天冬氨酸酯(PAE)脂肪族聚脲進行了一系列合成、表征及測試.研究發現,在實驗溫度范圍內(?80 °C～ 80 °C),三官能度PAE-F 擴鏈劑聚脲(硬段剛度更大)的儲能模量比直鏈二胺PAE-a 擴鏈劑聚脲的儲能模量大,且硬段玻璃化轉變溫度更高,轉變區域更寬;增大軟段分子量,聚脲儲能模量降低,微相分離度增大.

Shahi 等[10]通過DMA 實驗和超聲實驗研究了聚脲軟段長度及硬段含量對材料性能的影響.實驗制備了PU105(VP1000 長軟段,低硬段含量)、PU605(VP650 中軟段,高硬段含量)以及PU-HB05(VP1000 與VP250 混合,硬段含量與PU605 一致),通過DMA 實驗及超聲實驗測量相應儲能模量和損耗模量.實驗發現,PU605 和PU-HB05 的儲能模量和損耗模量均大于PU105,且損耗峰更寬,計算得到的松弛譜也更平緩,而PU605 和PU-HB05 的動態模量、松弛譜均相當.這表明硬段含量與材料的線性黏彈性性能密切相關.

Holzworth 等[13]通過DMA 研究了聚脲軟硬段組分化學計量比對材料線性黏彈性性能的影響.研究人員制備了硬段化學計量指標(硬段物質的量/軟段物質的量)為0.9～ 1.2 的多組試樣并進行了?80 °C～50 °C、5 組頻率下的DMA 實驗,通過時溫等效得到了相應的主曲線、松弛譜.比較發現,隨著硬段組分比例增加: 聚脲玻璃化轉變溫度以上的儲能模量和損耗模量均增大,而玻璃化轉變溫度以下的模量大小幾乎一致;時溫轉換因子?溫度曲線更加陡峭,表明材料溫度敏感性增大;松弛譜峰形更加平緩,表明材料松弛時間分布更寬.

Li 等[19]對不同溫度(120 °C～ 200 °C)退火處理的聚脲進行了DMA 實驗比較,發現退火處理對材料橡膠平臺儲能模量有較大影響,退火溫度低于150 °C,橡膠平臺儲能模量略有降低;退火溫度高于150 °C,橡膠平臺儲能模量急劇減小;而退火處理對聚脲玻璃化轉變溫度以下的儲能模量幾乎無影響.結合紅外光譜、小角散射實驗及原子力顯微鏡對聚脲微結構的觀察,他們將原因歸于高溫下氫鍵和硬疇的破壞,以及恢復常溫后結構未完全回復.

這些針對聚脲軟硬組分以及退火處理的研究既表明了影響聚脲黏彈性的因素多樣,同時也展現了聚脲性能的可調節性.

1.2 大變形非線性黏彈性

防爆抗沖擊材料在爆炸沖擊載荷下往往經歷大變形直至最終破壞,認識聚脲大變形下的力學行為是提升和優化其防爆抗沖擊性能的前提.

Yi 等[22]通過材料試驗機和霍普金森壓桿研究了聚脲和聚氨酯在低應變率10?3～ 100s?1和高應變率103～ 104s?1下的單軸壓縮應力?應變關系(如圖5).實驗發現聚脲和聚氨酯均表現出應力?應變曲線的高度非線性,且加卸載過程中應力?應變曲線表現出遲滯回線形狀,二次加載出現軟化現象.對比不同應變率下的流動應力,發現聚脲和聚氨酯的應力水平均隨應變率的增加而增加,表現出明顯的應變率敏感性,且應力與應變率對數在低應變率和高應變率范圍內分別呈不同斜率的近線性關系,這表明了不同的應變率依賴性機制.他們認為聚脲在低應變率情況下表現的是類橡膠行為,在高應變率情況下表現的是類玻璃行為,結合DMA 實驗發現聚脲的這種轉變是由于其動態玻璃化轉變溫度隨應變率增大而增大.

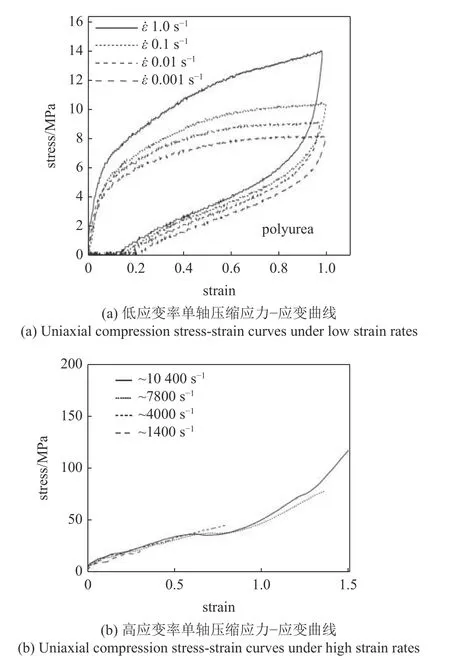
圖5 聚脲低、高應變率單軸壓縮應力?應變曲線[22]Fig.5 Uniaxial compression stress-strain curves of polyurea under low or high strain rates[22]

Amirkhizi 等[15]通過霍普金森壓桿對聚脲進行了高應變率壓縮實驗,包括常溫下的非側限壓縮以及不同溫度(273 K,294 K 和333 K)的側限壓縮.非側限壓縮結果與Yi 等[22]的結果一致,側限壓縮應力?應變曲線整體表現為線性關系,且具有一定的溫度相關性.

Roland 等[36]通過改造新型落錘試驗機實現了對聚脲中應變率下拉伸力學行為的研究,填補了低應變率材料試驗機和高應變率霍普金森桿的空隙.實驗得到了聚脲在0.06～ 573 s?1應變率范圍內的拉伸應力?應變曲線,同樣表現出明顯的應變率敏感性.同時,他們還對比了軟硬段組分不同化學計量比(軟段/硬段: 86%～ 106%)聚脲的拉伸性能,發現硬段組分增加,屈服應力增大,斷裂伸長比減小,斷裂強度增大,而韌性(應力?應變曲線與應變軸圍成的面積)幾乎不變.Qiao 等[37]在Roland 等[36]的基礎上補充了同種聚脲低應變率(5.3 × 10?4～ 5.1 × 10?2s?1)拉伸實驗,也對比了該應變率范圍下軟硬段組分化學計量比對材料性能的影響,實驗結果與Roland 等[36]結果一致.但即使兩組研究人員制備的聚脲組分一致,Qiao 等[37]制備的聚脲表現出更高的強度和更低的斷裂伸長比,這說明除了組分的影響,具體的制備過程對材料的性能也存在一定的影響.

Shim 等[38]通過一種液壓活塞驅動霍普金森壓桿對聚脲進行了中應變率壓縮實驗,獲得了101～103s?1中應變率范圍內的壓縮應力?應變曲線.通過與材料試驗機和傳統霍普金森桿獲得的數據進行比較,驗證了該設備測試數據的準確性.同時,對比不同應變下的流動應力與應變率的關系可以發現: 應變越大,應變率敏感性越高.

Sarva 等[39]通過Zwick 扭轉驅動材料試驗機(低應變率)、增強型伺服液壓試驗機MTS 810 (中應變率) 以及霍普金森壓桿(高應變率),對聚脲在10?3～ 103s?1應變率范圍內的壓縮力學行為進行了更全面的研究.實驗結果如圖6(a)所示,聚脲具有明顯的應變率敏感性,存在由低應變率下的橡膠態向高應變率下的類皮革態轉變的特點.實驗數據與Yi 等[22]和Roland 等[36]的結果具有一致性和互補性(如圖6(b)),這些數據也多次被后來的研究者用于聚脲本構模型的驗證[16-17, 40-41].

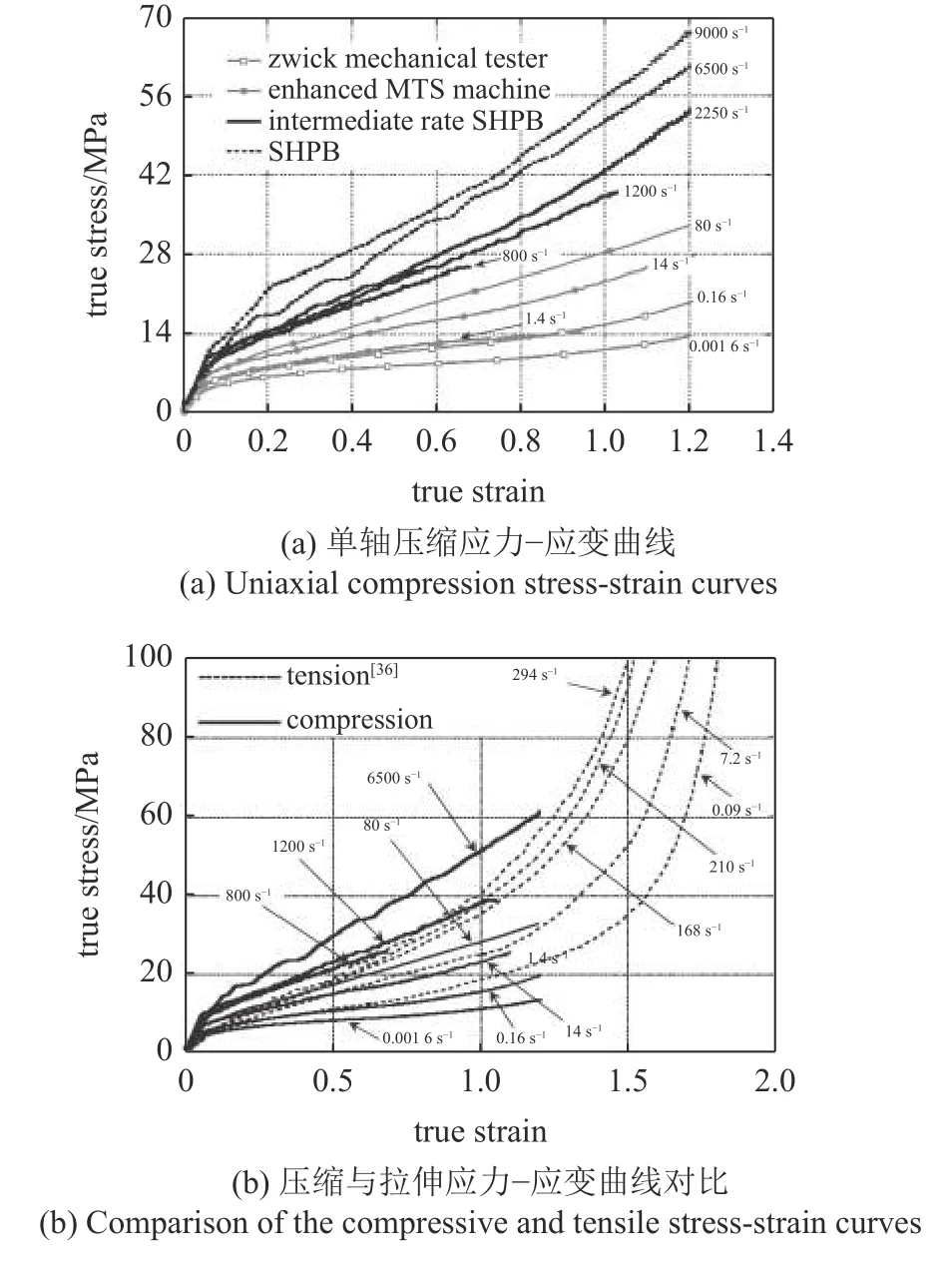
圖6 聚脲不同應變率下拉壓應力?應變曲線[39]Fig.6 Tensile and compressive stress-strain curves of polyurea under different strain rates[39]

隨著不同應變率范圍的加載實驗設備和方法的完善,越來越多的研究者針對聚脲寬應變率范圍內的大變形力學行為開展實驗研究[42-45].實驗均表明聚脲具有明顯的應變率效應,表現為初始彈性模量、屈服應力和斷裂強度等隨應變率增大而增大;拉伸曲線與壓縮曲線整體相似,但拉伸下具有更大的斷裂應變.

在聚脲常溫拉伸、壓縮力學性能得到廣泛研究的基礎上,研究人員開始關注聚脲的溫度敏感性,研究其不同溫度下的大變形力學行為.

Chevellard 等[29]對聚脲開展了室溫及以下溫度范圍(?43 °C～ 20 °C)內的低應變率(10?4～ 10?3s?1)Arcan 剪切實驗、單軸壓縮實驗和側限壓縮實驗.聚脲應力?應變曲線表現出明顯的應變率和溫度敏感性,隨著應變率增大或溫度降低,材料的模量、流動應力均增大.剪應力?剪應變曲線和單軸壓縮應力?應變曲線表現出非線性黏彈性,體應力?體應變曲線表現為近線性的關系.

Guo 等[46]針對兩種不同軟段長度的聚脲開展了常溫下的低應變率(0.001 s?1和0.1 s?1)壓縮實驗和?40 °C～ 20 °C 溫度范圍內的高應變率(3400 s?1～12000 s?1)壓縮實驗(如圖7).與Chevellard 等[29]低應變率下的結果一致,聚脲單軸壓縮應力?應變曲線高度非線性,而側限壓縮應力?應變幾乎為線性關系;聚脲高應變率下同樣表現出明顯的溫度敏感性和應變率敏感性,但側限壓縮應力?應變曲線表現出的溫度、應變率敏感性較非側限單軸壓縮顯著降低;相同加載條件下,PU605(短軟段聚脲)的應力均高于PU105(長軟段聚脲).

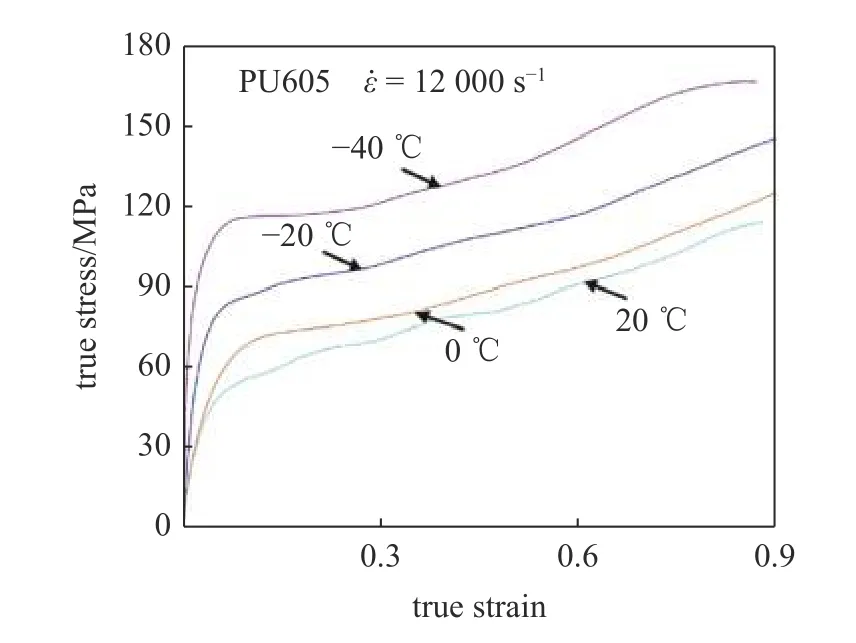
圖7 聚脲不同溫度下動態壓縮應力?應變曲線[46]Fig.7 Dynamic compression stress-strain curves of polyurea at different temperatures[46]

Miao 等[47]對聚脲進行了常溫下的低應變率(10?4～ 100s?1)和高應變率(10?3s?1)拉伸實驗,發現低應變率和高應變率拉伸具有相同的近線性的應變率敏感性以及相似的應變硬化行為.進一步通過間歇加載實驗(每加載一段位移后保持一定時間,然后繼續加載) 與連續拉伸實驗應力?應變曲線對比發現(圖8),應變率為0.001 s?1的間歇加載實驗的應力與同樣應變率的連續加載實驗幾乎一樣,而應變率為0.1 s?1的間歇加載實驗的應力高于同樣應變率的連續加載實驗,這意味著材料變形過程中塑性功轉化為了熱,提高了聚脲的溫度(與Mott 等[48]對聚脲變形過程中溫升的測量結果一致),導致材料軟化,而這在應變率提高時更為明顯,這間接說明聚脲具有較高的溫度敏感性.

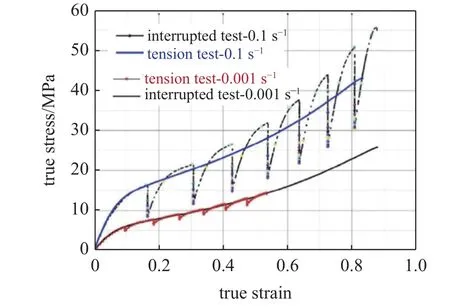
圖8 聚脲不同應變率下間歇拉伸與連續拉伸應力?應變曲線[47]Fig.8 Stress-strain curves of polyurea under the interrupted and continuous tensile experiments at different strain rates[47]

Liu 等[49]針對一種添加了少量納米碳化硅的聚脲材料開展了室溫及室溫以上溫度(20 °C～ 80 °C)的高應變率壓縮實驗.與低溫情況一致,聚脲在室溫以上同樣表現出應變率及溫度敏感性.

Gong 等[41]針對一種典型聚脲系統地研究了其低溫到高溫(?30 °C～ 60 °C)下的靜(10?3s?1)、動態(103s?1)壓縮力學行為(如圖9).與其他研究數據一致,聚脲應力?應變曲線表現出明顯的非線性、應變率和溫度敏感性,初始模量和流動應力均隨應變率增大或溫度降低而增大.

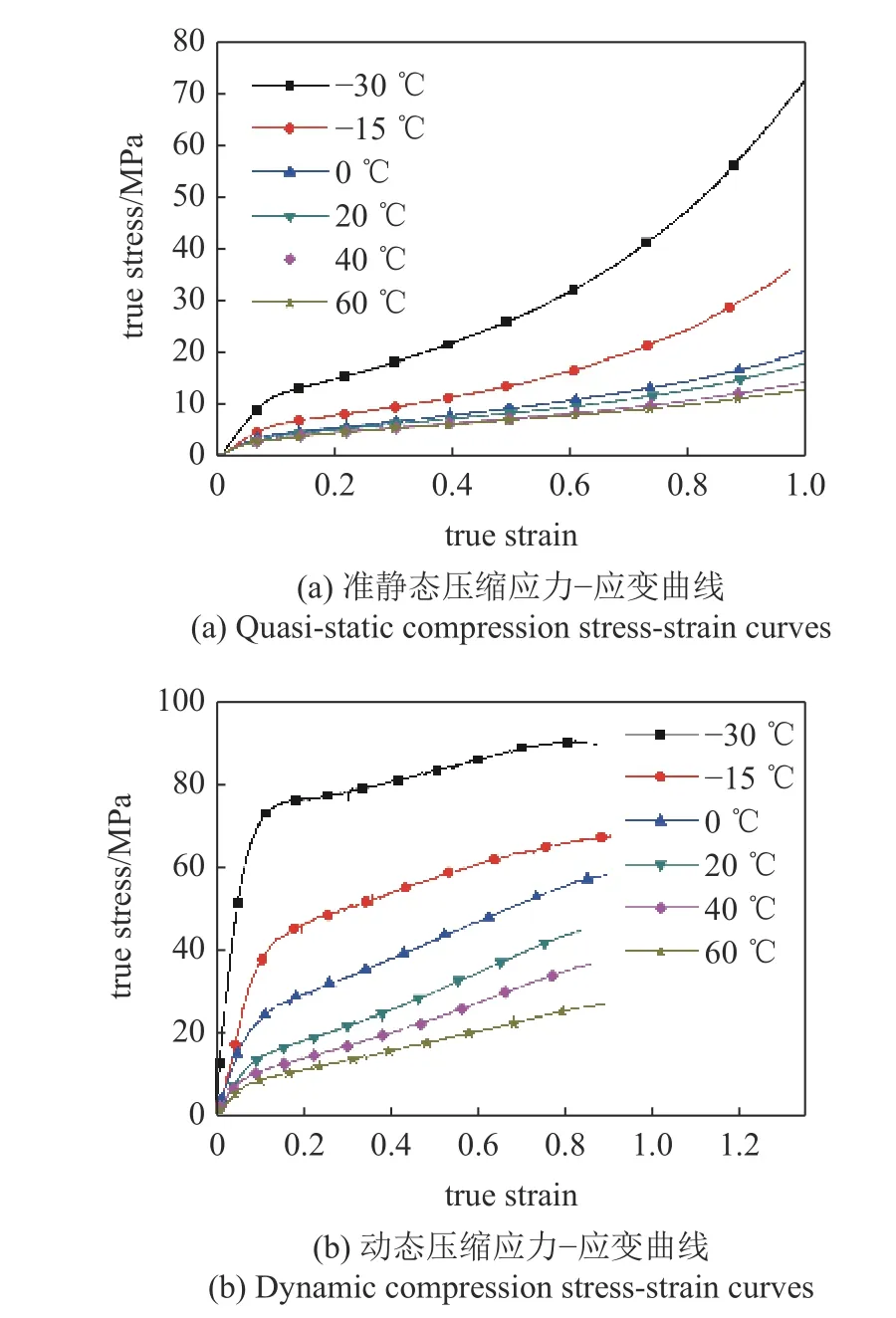
圖9 聚脲不同溫度下靜動態壓縮應力?應變曲線[41]Fig.9 Quasi-static and dynamic compression stress-strain curves of polyurea under different temperatures[41]

2 聚脲本構模型

隨著對聚脲力學性能研究的不斷深入,應變率、溫度敏感性等宏觀變形特點得到了較充分的認識,另一方面,針對聚脲特有微結構的研究也在同步進行,如何有效建立兩者之間的內在關聯？如何通過數學、物理模型定量描述和有效預測聚脲彈性體的黏彈性力學行為？這些成為研究者們關注的重要問題.過去十幾年間,研究者們應用不同的建模方式,提出了多種針對聚脲的本構模型,并在一定范圍內對聚脲的力學行為實現了滿意預測.根據聚脲黏彈性模型建立時依據的主要框架及思想,可以將這些本構模型歸為以下3 類: 變形梯度乘法分解法、遺傳積分法以及應變?時間解耦法[41].需要說明的是,部分本構建模中可能涉及多種建模方法,文中將按照其主要建模方式進行歸類.下文將對以上3 種主要建模方式及其他建模方式的代表模型進行介紹.

2.1 變形梯度乘法分解法模型

不同于傳統小變形彈塑性理論中總應變加和分解為彈性應變和塑性應變的假設,變形梯度乘法分解法基于宏觀變形梯度可以乘法分解為彈性變形梯度和塑性變形梯度的原則,這使得其對大變形問題具有更好的適用性.通常以彈簧單元、塑性或黏性黏壺單元等通過并聯或串聯的方式描述模型,不同的單元組合可以用于表示材料不同的力學行為,因此不同的模型往往有不同的單元組合方式.此外,相同單元的力學模型可以有多種選擇,這也導致了通過這種方法建立本構模型的多樣性.對于聚脲材料,目前主要有以下6 個通過變形梯度乘法分解框架建立的本構模型.

2.1.1 Qi-Boyce 模型

Qi 等[50]最早針對聚氨酯材料建立了以變形梯度乘法分解法為框架的本構模型,由于聚氨酯是一種和聚脲一樣具有微相分離結構、且力學響應相似的彈性體材料,因此該模型也可用于描述聚脲材料的力學行為.

Qi 等[50]基于聚氨酯低應變率下應力?應變曲線表現出來的應變率敏感性、循環加載下應力?應變曲線表現的遲滯性、循環軟化等特點,提出將聚氨酯的應力?應變行為分解為一個時間無關(平衡構型)的超彈性分支和一個時間相關(偏離平衡構型)的黏彈?塑性分支的并聯,如圖10 所示,兩分支的變形梯度張量(超彈性分支變形梯度張量FN,黏彈?塑性分支變形梯度張量FV)均與宏觀變形梯度張量(F)一致,即F=FN=FV.

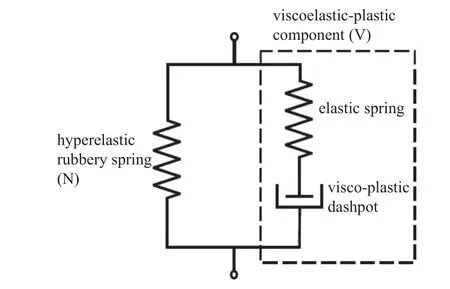
圖10 Qi-Boyce 模型的一維流變圖[50]Fig.10 One-dimensional schematics of the Qi-Boyce model[50]

Qi 等[50]認為平衡超彈性分支主要由軟基在變形過程中構型熵改變產生,可以由Arruda-Boyce 八鏈模型[51]描述,在此基礎上,考慮硬疇對軟基變形的放大作用,得到如下超彈性應力表達式[52]

對于聚氨酯循環軟化的特點,Qi 等[50]認為是由部分被硬疇阻塞而不能變形的軟基在分子鏈拉伸過程中逐漸被釋放導致,因此,提出了軟基等效體積分數隨最大分子鏈伸長比的演化方程

其中,A是與演化速率相關的一個常數,vss是飽和軟基等效體積分數,是分子鏈極限伸長比,是當前狀態下已經達到過的分子鏈最大伸長比.

黏彈?塑性分支由一個線性彈簧單元和一個非線性黏塑性黏壺單元串聯組成,變形梯度張量滿足乘法分解分別是此分支彈簧和黏壺的變形梯度張量).該分支應力可以由線性彈簧單元得到,即

其中,vh=1?vs是硬疇等效體積分數,是的雅可比行列式,Le是4 階彈性剛度張量,是線性彈簧單元的左伸長張量.

考慮黏塑性變形無旋的情況(旋率=0),黏彈?塑性分支的速度梯度張量可以做如下分解

其中,vh0是初始硬疇等效體積分數,s0是初始無熱剪切強度.

至此,平衡超彈性分支和非平衡黏彈?塑性分支的應力均已得到,總的宏觀應力由這兩分支的應力疊加得到.Qi-Boyce 模型是較早針對具有微相分離結構彈性體建立的本構模型,模型以硬疇、軟基的等效體積分數及其演化方程唯象地建立了模型與微觀微相分離結構的關系,可以較好地擬合聚氨酯在低應變率下的應力?應變曲線,從而有效預測低應變率下的應變率敏感性、遲滯以及循環軟化特點.但模型認為所有率相關效應是由硬疇(以及硬疇/軟基交界面)貢獻,而沒有考慮軟基的黏彈性;另外,單一熱激活能模型對高聚物松弛過程多分散的特點難以表征,因而對更寬范圍的應變率敏感性較難預測.

2.1.2 Jiao 模型

與Qi-Boyce 模型類似,Jiao 等[53]基于變形梯度乘法分解框架將聚脲總的宏觀響應分解為時間無關的超彈性分支(A) 和時間相關的黏彈?塑性分支(B).不同之處是其黏彈?塑性分支考慮了壓力敏感性,且超彈性分支應力用Neo-Hookean 模型[54]進行描述,即

其中,σA表示超彈性分支應力,2C10是該分支初始剪切模量,B′是左柯西?格林變形張量B=FFT的偏量,KA是該分支的體積模量,I是單位二階張量.

黏彈?塑性分支的應力同樣由線性彈簧單元得到,表示為一個偏應力與體應力之和,即

其中,Ap等于內聚能的 1/6,由擬合得到.

與Qi-Boyce 模型相同,需要定義黏壺的流動法則,且考慮塑性流動是無旋的,即

其中,υ是激活體積,τ0=?G/υ是剪切強度(?G是激活能),α=?(p)/υ(? (p)是壓力激活體積).表達式(12)與Qi-Boyce 模型的式(6)不一樣的地方是加入了壓力敏感項(即p相關項),用于表征壓剪板實驗中發現的聚脲剪切強度的壓力敏感性,即隨加載壓強增大,材料剪切強度增大.

Jiao 等[53]將模型應用于模擬壓剪板沖擊實驗,對于法向速度,模擬結果與注射成型試樣的實驗結果較為一致,與擠壓成型試樣的實驗結果存在偏差;但剪切波到達后試樣的剪切響應與實驗結果都較為一致,體現出了聚脲剪切強度的壓力敏感性.然而與Qi-Boyce 模型一樣,Jiao 模型僅對實驗涉及的很小應變率范圍內的結果擬合較好;另外Jiao 模型沒有考慮材料的微結構關聯性,以及材料軟化的特點.

2.1.3 Shim-Mohr 模型

Shim 等[14]針對聚脲開展了不同應變率下的分段壓縮實驗,即加載或卸載過程分為多段應變進行,每段加載或卸載后保持應變,記錄材料的應力松弛過程(Qi 等[50]針對聚氨酯進行了單一應變率下的多步壓縮實驗).實驗發現聚脲的“平衡”應力隨應變率增大而增大,即聚脲不存在所謂的“平衡”分支.因此,他們提出了雙麥克斯韋單元并聯的本構模型,如圖11 所示.A 分支主要描述聚脲軟基相關的力學行為,由一個非線性超彈性彈簧單元和一個非線性黏壺單元組成;B 分支主要描述聚脲硬疇相關的力學行為,由一個線性彈簧單元和一個非線性黏壺單元組成.

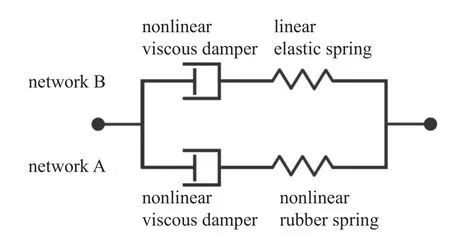
圖11 Shim-Mohr 模型的一維流變圖[14]Fig.11 One-dimensional schematics of the Shim-Mohr model[14]

A 分支的非線性彈簧單元由Gent 橡膠彈性模型[55]描述,其偏應力公式為

對于黏壺的流動法則,A 和B 分支具有相同的形式,表示為

A 和B 分支黏壺的不同之處在于其等效Mandel應力和等效黏性變形率的定量關系不一樣.它們分別是

疊加A 和B 分支的應力得到宏觀應力的偏量部分,對于體積變形,Shim 等[14]使用如下形式

Shim-Mohr 模型沒有采用Qi-Boyce 模型、Jiao 模型中常用的Zener 流變模型(即平衡超彈性彈簧單元并聯一個麥克斯韋單元),對軟基和硬疇的率相關性均進行了考慮.模型計算的松弛模量與聚脲在10?3～103s時間內的實驗結果吻合較好,對聚脲在10?3～101s?1應變率范圍內的壓縮應力應變曲線也具有較好的擬合效果,但卸載過程模型過于剛硬,卸載的殘余變形也比實驗結果偏大.

2.1.4 Grujicic 模型

Grujicic 等[16]建立了一個基于聚脲分子水平微結構的率無關彈塑性模型.Grujicic 等[16]認為聚脲微觀結構上包含3 種區域: 純軟基區域、軟基與完整硬疇區域、軟基與破壞的硬疇區域;因而力學模型上將聚脲響應分為3 個分支,如圖12 所示.小應變下,聚脲為彈性響應,模型僅包含一、二分支: 第一分支是超彈性彈簧,用于表示純軟基區域;第二分支包含一個剛性結構單元和超彈性彈簧,分別表示幾乎不可變形、完整的硬疇以及相鄰的軟基.當變形增大到一定值,硬疇開始發生破壞、塑性流動,此時加入塑性結構單元和超彈性彈簧(第二分支逐漸向第三分支轉化)來表示.

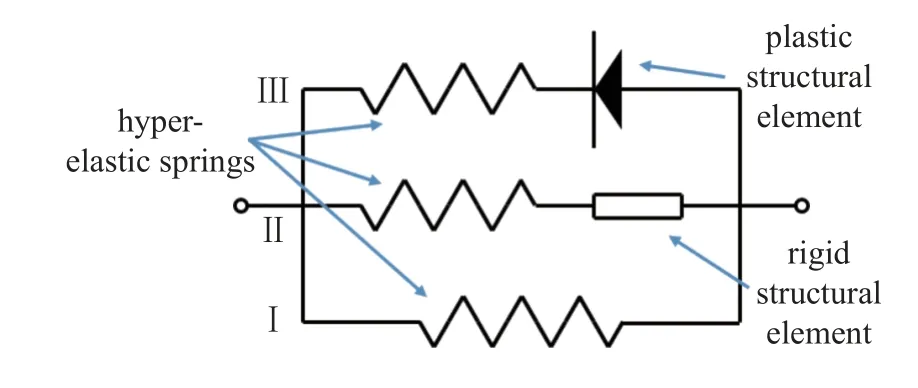
圖12 Grujicic 模型的流變圖[16]Fig.12 Schematics of the Grujicic model[16]

考慮到3 種區域隨機分布且相互連接,Grujicic 等將Arruda-Boyce 八鏈模型[51]中的超彈性分子鏈替換為圖12 中的3 個并聯分支結構,將宏觀變形與3 條分支的變形聯系起來,即其中,λchain表示每個分支的伸長比,I1是宏觀左柯西?格林變形張量的第一不變量.因此,類比八鏈模型的應變能密度函數,得到模型小變形下的應變能密度函數為

其中vh是硬疇體積分數.

柯西應力可以由下式得到

其中,B′是左柯西?格林變形張量的偏量,p是靜水壓,采用Tait 狀態方程,即

其 中,V0是參考 比體積;θ是溫度;a0,a1,a2,C,b0和b1是材料常數.

將式(19)代入式(21),可以得到單軸加載應力表達式為

隨著變形增大到特定值,硬疇開始發生塑性流動,引入第三分支,塑性結構單元考慮為理想塑性單元.因此,第三分支保持常應力 σy.總的應力在式(23)的基礎上加上vIIIσy,并假定體積不變.

第二分支向第三分支轉變,第三分支體積分數演化由下式確定

其中,是第二分支的初始體積分數,λchain,max表示已經達到的最大伸長比,是第三分支出現時的臨界伸長比,aIII是材料常數.

對于聚脲存在的軟化現象,考慮第三分支剪切模量是氫鍵破壞參數的線性函數(μIII=μ(1?d)),氫鍵破壞參數與變形關系為

其中,c是材料常數.

Grujicic 模型充分考慮了聚脲微結構以及演化的特點,對聚脲力學響應與微結構的關系有一定認識.但最大的問題在于模型是率無關的,這對于聚脲材料的應變率敏感性,以及其常用場景抗沖擊來說是不適用的;其次,模型中演化方程多為唯象提出,相應的材料常數無實際物理意義.

2.1.5 Cho-Boyce 模型

Cho 等[56]在Qi-Boyce 模型[50]基礎上提出了一個可以細致描述聚脲軟硬相力學行為的模型,如圖13 所示.宏觀響應由硬疇的響應和軟基的響應組成,且它們又包含相應的分子間作用和分子鏈網絡拉伸兩部分.Cho-Boyce 模型的大變形運動學公式與Qi-Boyce 模型一樣,包括變形梯度張量的乘法分解、速度梯度張量、塑性或黏性變形無旋假設、流動法則等.不同地方包括相應的超彈性彈簧模型、塑性或黏性剪切應變率表達式、軟化相關演化方程.

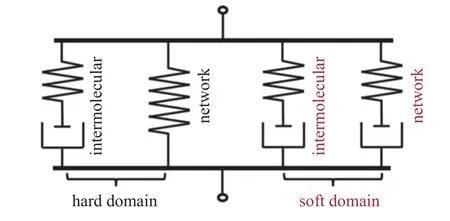
圖13 Cho-Boyce 模型的一維流變圖[56]Fig.13 One-dimensional schematics of the Cho-Boyce model[56]

對于分子間作用分支,其彈簧單元采用了可壓縮Neo-Hookean 模型,應力表達式為

其中,α代表“IH(分子間作用?硬疇)”或“IS(分子間作用?軟基)”,μα是初始剪切模量,是彈簧的左柯西?格林變形張量的偏量,K是體積模量.分子間作用分支上黏壺單元的率相關屈服過程用熱激活模型描述,相應的等效塑性剪切應變率表達式為

對于分子鏈網絡分支,其彈簧單元選用Arruda-Boyce 八鏈模型[51]進行描述,即

其中,β代表“NH(分子鏈網絡?硬疇)”或“NS(分子鏈網絡?軟基)”,Nβ是單分子鏈中等效鏈段數,λc,β=是平均分子鏈伸長比.軟基的分子鏈網絡分支還包含一個非線性黏壺,用于描述其黏彈性性質,其等效黏性剪切應變率表示為

對于聚脲的軟化性質,Cho-Boyce 模型考慮了硬疇、軟基對應分子間作用分支的軟化和硬疇分子鏈網絡分支的軟化.分子間作用分支的軟化體現為剪切強度和剪切模量隨塑性應變增大而減小,具體演化方程為

其中,hα和mα是控制軟化速率的常數,sss,α和μss,α分別是穩態剪切強度和穩態剪切模量.硬疇分子鏈網絡分支的軟化考慮為隨變形增大,剪切模量減小,分子鏈極限伸長比 λlock或等效 鏈段數NNH增大分子鏈極限伸長比的演化方程為

其中,λss,lock是率相關的飽和分子鏈極限伸長比,slock是硬疇分子鏈網絡的破壞強度,其隨變形演化,是該分支的等 效應 力,c0,c1,c2,m和r是材料常數.分子鏈極限伸長比增大或等效鏈段數增加伴隨著剪切模量的減小,且保持如下關系

不同于前文中的模型僅能單獨擬合低應變率或高應變率的情況,Cho-Boyce 模型在同一組參數下可以同時與低應變率和高應變率實驗數據達到較好的吻合,這源于它不僅考慮了硬疇和軟基變形的率相關性,且分別考慮了相應相內分子間作用和分子鏈網絡的率相關性.此外,Cho-Boyce 模型還能較好地描述聚脲的軟化行為.然而,正是因為Cho-Boyce模型考慮了多種率相關因素,導致其形式較為復雜,材料參數較多.

2.1.6 Chu-Liu 模型

最近,針對聚脲受子彈沖擊加載的情形,Chu等[57]建立了一個考慮強非線性體積響應以及沖擊誘導剪切強化特點的聚脲本構模型.模型將總的應力響應分為體積響應和偏應力響應,偏應力響應又考慮為分子鏈網絡超彈性和分子間黏塑性的疊加,其一維流變圖與Qi-Boyce 模型一樣,即圖10.

對于體積響應,Chu 等[57]采用了Mie-Grüneisen狀態方程,壓強表達式為

其中,Γ0是Grüneisen 參數,ρ0是材料初始密度,e和e0分別是現時和初始內能密度,其演化方程可以表示為

其中,σ是柯西應力張量,D是變形率張量.pH是Hugoniot 狀態下的壓強,表達式為

其中,C0和S分別是 沖擊波波速US為粒子速度UP線性函數(即US=C0+S UP)的截距和斜率.

分子鏈網絡超彈性采用了Arruda-Boyce 八鏈模型[51],偏應力表達式與式(28)類似,但加入了熱軟化函數k(θ) 和沖擊強化因子χ,即

熱軟化函數采用如下指數關系

其中,ak和bk是常數,θr是參考溫度.

與Cho-Boyce 模型類似,Chu 等[57]考慮了分子鏈網絡隨變形的軟化,體現為初始模量減小和單分子鏈中等效鏈段數的增大.初始模量演化表達式為

其中,μN0是初始剪切模量,?是一個表征分子鏈排列取向程度的量,與Cho-Boyce 模型定義一致,即式(30),?0是相應的初始量,qm是控制軟化程度的常數.等效鏈段數的演化與Cho-Boyce 一樣,即保持式(36)成立.

對于分子間黏塑性,彈簧單元應力響應采用Neo-Hookean 模型,且加入了熱軟化函數和沖擊強化函數,表達式為

其中,k(θ)是熱軟化函數,表達式與分子鏈網絡一致即式(41),g(J)是沖擊強化函數,采用了如下Lennard-Jones 函數形式

黏壺的塑性流動考慮為無旋且與分子間作用偏應力張量共軸.為了考慮溫度、壓強對黏塑性的影響,Chu 等[57]加入了自由體積對黏塑性流動率的影響,定義相應的等效黏塑性剪切應變率為

其中,?fJ是等熵壓縮導致的自由體積變化,?fθshear是剪切變形溫升導致的自由體積變化,AJ和BJ是擬合常數,αV0是自由體積在常壓下的熱膨脹系數,mV是表征自由體積熱膨脹系數壓強敏感性的參數,?θshear是剪切變形導致的溫度變化.

最后,變形過程中溫度的演化同樣考慮為等熵壓縮和黏塑性剪切兩部分構成

其中,Cp=cpθ+dp是聚脲常壓下的比熱,假設與溫度線性相關.

Chu-Liu 模型對常溫下的低應變率和高應變率拉伸壓縮數據、對273 K～ 333 K 溫度范圍內的動態壓縮結果都有較好的擬合效果,與壓剪板沖擊實驗結果的比較也表明模型的有效性.借助該本構模型,Chu 等[57]進一步對聚脲涂層鋼板抗破片過程進行了模擬,很好地揭示了聚脲涂層抗沖擊耗能的機理.

2.2 遺傳積分法模型

遺傳積分是黏彈性理論的一個非常重要的概念,可以用于表示線性黏彈性模型的本構方程,如式(48)是一維情況下基于松弛模量E(t),以應變 ε (t)表示應力 σ (t)的線性黏彈性本構方程

其中的積分項即稱為遺傳積分.對于復雜高聚物材料,線性黏彈性模型一般不足以描述材料大變形下的非線性性質,研究者通常通過引入松弛模量隨變形變化的規律實現黏彈性模型的非線性化,如將平衡模量考慮為應變相關,假設變形導致材料松弛時間減小等.

2.2.1 Amirkhizi-Nemat-Nasser 模型

Amirkhizi 等[15]最早通過遺傳積分法建立了聚脲的線性黏彈性本構模型,且考慮了溫度敏感性及壓力敏感性.模型將總的響應分為體脹響應和偏量響應,體脹響應表示如下

其中,p為壓強,K是體積模量且與溫度滿足線性關系,即

其中,Kref是參考溫度 θref下的體積模量,mK是體積模量的溫度系數.

模型的偏量響應用遺傳積分表示為

其中,D′(τ) 是 τ 時刻變形率張量的偏量,Gref(t)是參考狀態下的松弛模量,ξ (t)是縮減時間,它是考慮溫度變化后的等效時間,具體為

其中,a(θ)是時溫轉換因子,用于考慮溫度和時間的等效關系.對于線性非晶高聚物,溫度范圍在玻璃化轉變溫度以上100 K 范圍內,a(θ)可以用WLF 方程[27]表示,即

其中,C1和C2是與參考溫度 θref相關的常數.在溫度效應的基礎上,Amirkhizi 等[15]引入了壓力效應,通過將其線性等效為溫度減小對時溫轉換因子產生的影響,得到

其中,Ctp是壓強溫度轉換系數.對于式(51)中的松弛模量,可通過多種函數形式表達,其中主要包括冪律形式和Prony 級數形式.冪律形式參數少、公式簡潔,但數值計算難實現;Prony 級數形式方便用于數值計算,但對于高聚物,尤其是松弛時間不均勻性較強的高聚物,通常需要較多級數項才能很好的擬合全時間段的松弛模量.Amirkhizi-Nemat-Nasser 模型選用了Prony 級數形式,即

其中,G∞是平衡剪切模量,n為級數項數,qi為第i個松弛時間,G∞pi是第i個松弛過程的松弛模量.

對于材料內溫度的演化,模型使用絕熱假定(高應變率),變形中耗散的機械能完全轉換為熱能,溫度變化率表達式為

其中,CV是恒容熱容,Wd是耗散功密度,(t) 是第i個松弛過程的耗散應變,定義為

Amirkhizi-Nemat-Nasser 模型對霍普金森桿實驗得到的不同溫度下聚脲側限壓縮結果具有較好的擬合效果,但對其無側限單軸壓縮結果擬合較差,中高應變下模型應力水平遠高于實驗.這主要是由于Amirkhizi-Nemat-Nasser 模型的偏量響應是基于線性黏彈性模型建立的,沒有考慮真實材料的非線性黏彈性.因此,模型僅對體積變形主導的情況具有較好的預測,而很難模擬剪切變形主導的過程.

2.2.2 Li-Lua 模型

不同于Amirkhizi-Nemat-Nasser 模型是基于線性黏彈性,Li 等[17]建立了聚脲的非線性黏彈性模型.模型將總的響應分為低應變率下的超彈性響應和高應變率下不可忽略的黏彈性響應.

他們考慮準靜態下的應力完全由超彈性響應提供,并采用了Ogden 超彈性模型[58],相應的應變能密度函數為

其中,μi和 αi是材料參數,λ1,λ2和λ3是宏觀變形的主伸長比.通過應變能密度函數對格林應變的偏導可以得到第二類P-K 應力,再結合第二類P-K 應力與柯西應力的關系、體積不變假定以及單軸加載橫向應力為零的條件,可以得到軸向柯西應力為

對于率相關黏彈性響應,模型采用了非線性黏彈性模型,應力表達式為

其中,pv是黏彈性響應的壓強,A1和A2是常數,I2是右柯西?格林變形張量的第二不變量,是格林應變率張量,Gv(t)是不包含平衡模量的松弛模量函數,同樣采用Prony 級數形式.通過考慮單軸加載橫向應力為零,便可以得到軸向黏彈性應力.疊加超彈性應力和黏彈性應力得到總的宏觀應力.

Li-Lua 模型模擬結果與不同應變率的單軸壓縮數據吻合較好,這源于其是非線性黏彈性模型.但模型沒有給出體積響應本構方程,須通過邊界確定,因此Li-Lua 模型適用于簡單邊界條件加載情況;此外,Li-Lua 模型中Ogden 模型和Prony 級數需要的參數較多,與Amirkhizi-Nemat-Nasser 模型不同,該模型沒有考慮溫度、壓強效應.

Zhang 等[59]在Li-Lua 模型的基礎上,進一步發展了適用于聚氨酯材料的本構模型.他們用三參數Mooney-Rivlin 模型替代Ogden 超彈性模型,大幅減少了材料參數;黏彈性模型中考慮了各參數的溫度、應變率相關性,使得模型也可以描述材料的溫度敏感性.

2.2.3 Chevellard-Liechti 模型

為了修正Knauss 等[60-61]經典自由體積黏彈性模型無法描述高聚物剪切變形主導的非線性黏彈性行為的問題,Popelar 等[62-63]曾建立了剪切修正自由體積本構模型,并針對環氧樹脂和聚氨酯材料進行了驗證.Chevellard 等[29]將該模型應用于聚脲材料,擬合得到了聚脲本構模型及相應參數.模型將材料的響應分為體脹響應和剪切響應,可以由玻爾茲曼疊加原理或遺傳積分表示,即

其中,Kr和μr表示相應的橡膠態體積和剪切模量,Kg和μg表示相應的玻璃態模量,τc表示特征松弛時間,q是表示松弛時間離散度的常數.

不同于Amirkhizi-Nemat-Nasser 模型中轉換因子a僅通過WLF 經驗公式與溫度相關,Chevellard-Liechti 模型采用了自由體積模型,轉換因子a通過Doolittle 方程[64]與自由體積分數相關聯,即

其中,B是常數,f0是參考狀態的自由體積分數.在Knauss 等[60-61]提出的經典自由體積黏彈性模型中,自由體積分數假設為溫度、溶劑濃度和體脹應變的線性函數,即

其中,αV是自由體積的熱膨脹系數,βV是溶劑濃度改變導致的自由體積膨脹系數,δ是體應變導致的自由體積膨脹系數.

因此,將式(66)代入式(65)得到轉換因子與溫度、溶劑濃度和體應變的關系.在不考慮溫度及溶劑的情況下,δ εkk項的引入使得該黏彈性模型具有非線性性質,然而僅引入體脹對自由體積的影響不能描述材料剪切變形主導情況下的非線性黏彈性響應,因此,Popelar 等[62-63]仿照體脹相關項唯象地加上了剪切變形相關項,表達式為

其中,Bd和fd是體脹相關常數和初始自由體積,Bs和fs是剪切相關項參數,εeff是等效應變.由于式(67)中剪切修正項的引入,對于純剪這種幾乎無體積變形的加載情況,黏彈性模型也是非線性的.

Chevellard-Liechti 模型通過松弛實驗、Arcan剪切實驗、受限壓縮實驗以及一組單軸壓縮實驗結果擬合材料參數,并通過其他常溫及低溫下、不同低應變率單軸壓縮實驗結果驗證了模型的效果.通過在經典自由體積非線性黏彈性模型基礎上引入剪切修正項,擴大了該模型的適用性.但剪切修正項僅在轉換因子公式上唯象引入,沒有深入考慮自由體積的演化機制.

2.2.4 Gong-Chen-Dai 模型

不同于Chevellard-Liechti 模型唯象地對轉換因子進行剪切修正,Gong 等[41]從微觀角度引入了剪切誘導自由體積的機制,并給出了自由體積隨剪切變形的演化方程,進而建立了基于自由體積的聚脲非線性黏彈性本構模型.

模型首先從分子層面認識聚脲變形過程中的微觀運動,包括分子鏈段相對運動、分子鏈網絡的拉伸以及共價鍵的微小拉伸,它們分別產生了宏觀上的黏彈性響應、熵彈性響應以及能彈性響應.

分子鏈段相對運動產生的黏彈性剪應力通過遺傳積分描述,即

不同的是,分母中的減號換成了加號,可以有效避免t=τc時的奇異性.式(69)應用到式(68)時不包含時間無關的Gr項,而是由下文中的非線性熵彈性和能彈性響應代替.

用于計算縮減時間的轉換因子a仍然通過Doolittle 方程即式(65)與自由體積分數關聯.不同于Chevellard-Liechti 模型唯象地對轉換因子進行剪切修正,Gong 等[41]從微觀角度引入了剪切誘導自由體積的機制,即剪切變形導致聚脲硬疇、氫鍵破壞,從而導致自由體積增加.相應的自由體積分數的率演化方程如下

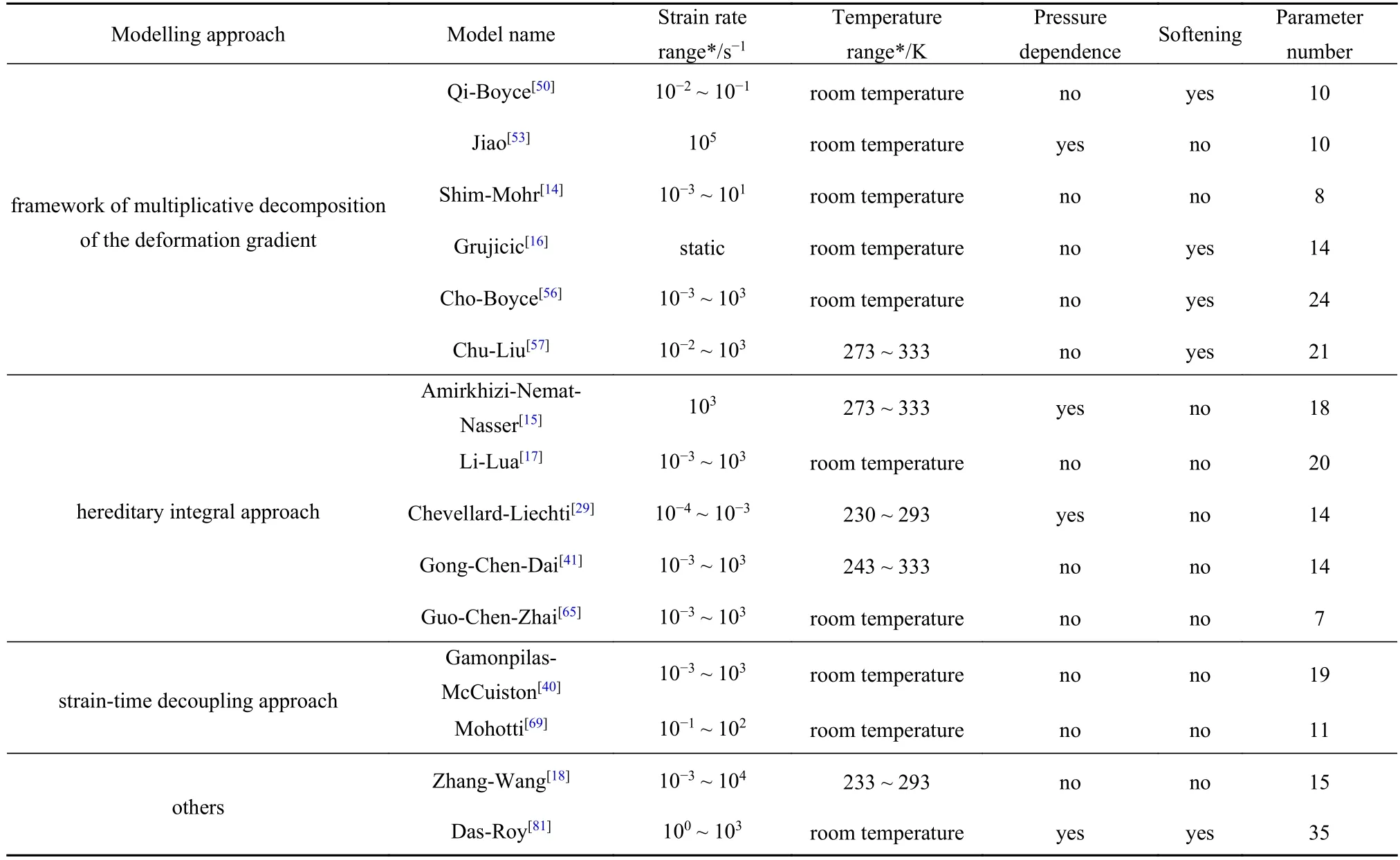
其中,式(70)前三項與Knauss 等[60-61]的經典自由體積黏彈性模型中的自由體積演化表達式即式(66)一致,但在Gong-Chen-Dai 模型中以率形式表達,ε ˙eff是等效應變率,δs是單位等效應變導致的自由體積分數變化,是一個隨自由體積分數變化的系數,即式(71),δs0是常數,fc是臨界自由體積分數,當f>fc,剪切變形不再產生新的自由體積.式(71)表示當f

分子鏈網絡的拉伸產生熵彈性響應,Gong-Chen-Dai 模型采用Arruda-Boyce 八鏈模型[51],應力為

其中nc是分子鏈密度,kB是玻爾茲曼常數,θ是溫度,N是單分子鏈中等效鏈段數,λchain是分子鏈等效伸長比,L?1(·)表示朗之萬函數的逆函數.為了考慮不同溫度下的熵彈性應力,在原八鏈模型基礎上,Gong 等[41]考慮了分子鏈密度nc的溫度相關性.假設分子鏈總數保持不變,結合高聚物比體積在玻璃化轉變溫度上下隨溫度以不同斜率線性變化,且模型僅考慮玻璃化轉變溫度以上范圍,可以得到如下關系

其中,A1和A2是常數.

最后,考慮到聚脲相較于一般彈性體具有更高的初始模量,結合其微觀上微相分離結構中硬疇對軟段運動的約束作用,Gong-Chen-Dai 模型加入了由共價鍵的微小拉伸導致的能彈性響應,具體應力為

其中,σmax是能彈性最大應力,ε0是參考應變.

由以上3 部分響應疊加得到整體宏觀響應,另外Gong-Chen-Dai 模型的體積響應采用了Amirkhizi-Nemat-Nasser 模型相同的形式,即式(49)和式(50).Gong-Chen-Dai 模型可以很好地預測聚脲在較寬的溫度范圍(?30 °C～ 60 °C)和較寬的應變率范圍(10?3～103s?1)內的力學響應行為,且因其從微觀層面引入剪切誘導自由體積的機制,模型可以得到材料自由體積隨變形的演化過程,可以用于進一步分析聚脲微結構與宏觀性能的關系.由于實驗集中于單軸壓縮模式,體積變形為小量,因此模型驗證過程中忽略了式(70)中的體脹項參數.但在高壓加載條件下,若材料體積變形明顯,其對自由體積的影響不可忽略,需要完整考慮剪切變形和體積變形的影響.

2.2.5 Guo-Chen-Zhai 模型

Guo 等[65-66]將彈性體材料的應變能密度函數考慮為時間無關的超彈性應變能和應變歷史相關的黏彈性應變能的疊加,即

根據熱力學框架的推導可以得到應力與應變能的關系式如下

其中,p是靜水壓,ρ0是材料密度,I1,I2和I3是左柯西?格林變形張量B的第一、第二和第三不變量.

對于超彈性應變能函數,Guo 等采用了Attard和Hunt[67]建立的有限變形超彈性模型,表達式為

其中,αh,βh和γh是材料常數.

對于黏彈性應變能,Guo 等[65-66]采用式(78)所示的遺傳積分形式,其中變形能耗散因子g(t)由三參數Mooney-Rivlin 模型(應變相關)和單一松弛時間的指數衰減函數(時間相關)組成,即

其中,τ0是松弛時間,aMR,bMR和cMR是Mooney-Rivlin 模型參數,E是格林?拉格朗日應變張量.

將式(77)和式(78)代入式(75),再代入式(76),得到相應的應力表達式.Guo-Chen-Zhai 模型對聚脲低、高應變率下的受限壓縮實驗數據[46]和中、高應變率下的非受限單軸壓縮實驗數據[39]具有較好的擬合效果,且模型同樣適用于如炭黑填充橡膠、硅橡膠等彈性體.但模型中靜水壓需由邊界條件確定,這降低了模型對復雜加載情況的適用性.

2.3 應變?時間解耦法模型

應變?時間解耦法假設材料本構響應中與應變相關的項和與時間相關的項不存在耦合關系,可以分別單獨考慮.通過分別建立應變相關項和時間相關項兩部分的具體形式后,進行組合,得到完整的本構模型.

2.3.1 Gamonpilas-McCuiston 模型

通過分析Sarva 等[39]獲得的聚脲應力應變數據,Gamonpilas 等[40]發現聚脲相同應變下的應力對數?加載時間(不同應變率)對數呈線性關系,且不同應變下的曲線保持相互平行,因此認為聚脲的應力可以表示為應變相關項乘以時間相關項,即

其中,σ0(ε) 是瞬時應力,與時間無關,g(t)是時間相關的松弛函數,沒有量綱.

對于瞬時應力,Gamonpilas-McCuiston 模型采用了九參數Mooney-Rivlin 模型[68],對于單軸加載情況,軸向真應力表達式為

其中,C01,C10,C11,C20,C02,C21,C12,C30和C03是材料常數,I1和I2是左柯西?格林變形張量第一和第二不變量.

時間相關松弛函數采用了Prony 級數形式,即

其中,τi是松弛時間,g∞和gi是無量綱常數,且滿足

Gamonpilas-McCuiston 模型建立的思路較為簡單,對聚脲不同應變率的拉伸壓縮數據也具有較好的擬合效果.但模型僅從一維角度建立,未考慮材料的可壓縮性,對更復雜的加載情況不具有適用性,且模型擬合參數較多.

2.3.2 Mohotti 模型

Mohotti 等[69]同樣采用應變?時間解耦法,從應變能密度角度出發建立聚脲的本構模型.傳統的Mooney-Rivlin 模型[68,70]不考慮加載歷史,與應變率無關,限制了其在彈性體不同加載速率時的應用.他們對Mooney-Rivlin 模型進行了應變率相關性的修正.

Mohotti 等[69]針對聚脲開展了中應變率拉伸實驗,實驗發現由應力?應變曲線得到的應變能密度與加載應變率的對數呈近乎線性關系,因此提出如下率相關應變能函數

其 中Cij和D是材料常數,是等容左柯西-格林變形張量第一和第二不變量.

應力表達式仍采用超彈性材料應力與應變能密度的關系式,單軸加載下軸向應力為

Mohotti 等[69]提出的率相關Mooney-Rivlin 模型可以較好地擬合實驗得到的中應變率拉伸應力應變數據.但模型過于簡單,僅針對一維恒定應變率的情況進行建模,復雜加載情況下模型的適用性未知.

Wang 等[42]在此基礎上進一步改善模型,將式(82)中率相關項即替 換為(其中Ar和Br是常數,且在低中應變率和高應變率下具有兩組不同的數值,用于描述聚脲不同的應變率敏感性),這使得模型對更寬應變率范圍的應力?應變關系具有較好的預測.

2.4 其他模型

除了上述模型以外,Zhang 等[18]將聚脲應力?應變曲線簡化為雙段線性關系,并考慮相應模量、屈服應力等的溫度和應變率敏感性,這些敏感性關系式在玻璃態高聚物中得到了Richeton 等[71-72]和Yu 等[73-74]的系統研究.此外,常被用于非晶合金[75-77]和其他高聚物[78-80]本構描述的構型溫度概念也被Das 等[81]應用到聚脲中.

2.4.1 Zhang-Wang 模型

Zhang 等[18]針對聚脲提出一個簡易的本構模型,模型考慮了單軸受限壓縮和非受限壓縮兩種情況,因此將總的軸向應力分為靜水壓和零壓應力疊加,而零壓應力與軸向應變的關系簡化為屈服前的線彈性段和屈服后的線性超彈性段,即

其中,αp是壓力敏感系數,σp=0是靜水壓為零時的軸向應力,E是非受限單軸壓縮初始線彈性模量,σy是屈服應力,Eh是屈服后硬化模量.

實驗應力?應變曲線得到的屈服應力表現為低應變率 (10?3～10?1s?1)下應變率不敏感,高應變率(103～ 104s?1) 下應變率敏感,且實驗溫度范圍(233 K～ 293 K)內,屈服應力隨溫度增加近乎線性減小.因此,Zhang-Wang 模型參考Richeton 等[72]的模型給出了如下屈服應力與溫度、應變率的關系式

其中,σy0是溫度為0 K 時的屈服應力,cy是常數,V是激活體積,是特征應變率,n1是一個表征鏈段運動的常數.

初始線性模量的溫度相關性采用了Mahieux等[82]通過考慮次級鍵斷裂強度韋伯分布得到的模型,應變率相關性采用了Richeton 等[71]提出的模型,可以表示為

其中,Eref是參考模量,是選定的參考應變率,sr是模量的應變率敏感系數,m1是模量與溫度相關的指數,θg,ref是參考應變率下的玻璃化轉變溫度,和是WLF 方程[27]的參數.

屈服后的超彈性段采用簡單的線性應力?應變關系,模量為式(85)中的Eh,從實驗應力應變曲線發現其溫度不敏感,僅與應變率相關,因此采用了如下關系式

其中,A,B和n2是常數.

Zhang-Wang 模型將聚脲的應力應變關系簡化為以屈服為分界點的雙段線性關系,并給出了兩個線性模量及屈服應力與溫度、應變率的關系式,模型預測可以大致與實驗應力應變曲線吻合.模型的簡化忽略了聚脲應力應變關系的細節,且不能描述材料更大應變下的極限伸長硬化階段.另外,模型適用于單軸加載情況.

2.4.2 Das-Roy 模型

Das 等[81]應用基于構型溫度(或有效無序溫度)的非平衡熱力學框架對聚脲本構關系進行了建模.該框架將材料考慮為緩慢演化的構型子系統和快速演化的振動子系統的耦合,不同子系統有相應的熱力學溫度、內能、熵、自由能等,子系統間由于溫度差導致能量傳遞,從而相互耦合.

對于聚脲,由于其存在微相分離結構,其微觀松弛過程不是單一的,而是包含軟基和硬疇的松弛過程,因此他們考慮了硬疇和軟基的兩個構型溫度和一個系統振動溫度.模型首先考慮材料總的內能、熵及自由能可由各子系統相應量通過混合率公式得到,即

其中,Y表示內能 ε、熵 η 或自由能 ψ,c 1表示軟基構型子系統,c 2表示硬疇構型子系統,k 表示振動子系統,vh是硬疇體積分數.將上式代入熱力學第一、第二定律,推導可得如下一般本構關系

其中,S是第二類P-K 應力,C是右柯西?格林張量,θc1,θc2和 θk分別是軟基構型溫度、硬疇構型溫度和振動溫度.根據以上表達式可知,建立具體形式的自由能函數代入可得到本構表達式.他們分別定義了兩個構型子系統和一個振動子系統的自由能,再根據式(90)得到系統總的自由能表達式.

在得到具體本構表達式后,需要進一步得到各溫度、內變量的演化方程.引入構型子系統與振動子系統間的能量傳輸,并將一般本構關系式(91)和式(92)代入,可將熱力學第一定律分解為如下3 個方程,分別對應3 個溫度的演化方程

其中,qk,qc1和qc2分別是從振動子系統、軟基構型子系統和硬疇構型子系統流出的熱流,qck1和qck2分別表示軟基構型子系統和硬疇構型子系統與振動子系統的熱交換,這體現了構型子系統與振動子系統間的耦合.

為簡化耗散不等式,進一步定義如下熱流傅里葉關系

其中,gci和gk分別是構型子系統和振動子系統的溫度梯度,kci和kk是相應的導熱系數,kcki是構型子系統與振動子系統間的導熱系數,由力學相關分量和熱學相關分量組成,控制構型溫度隨變形演化到穩定值,控制材料無載荷下的結構松弛行為.

利用熱流傅里葉關系簡化后的耗散不等式為

Das-Roy 模型可以較好的擬合聚脲常溫下不同應變率的壓縮實驗數據,也能反映材料循環加卸載軟化的特點以及拉壓不對稱性.模型從物理的角度出發應用了構型溫度的概念,且是在非平衡熱力學框架下建立,這使得模型較為嚴謹.而同時,這也導致了模型構成較為復雜,涉及參數多達35 個.

2.5 模型對比

為了更加直觀的對比各模型的區別,表1 列出了以上各聚脲本構模型經實驗數據驗證的應變率范圍、溫度范圍、是否考慮壓力敏感性、是否考慮軟化行為,以及模型參數的數量.

從適用的應變率范圍來看,變形梯度乘法分解框架模型的應變率范圍往往與其模型參數的數量正相關,這是由于聚脲微觀上具有非常寬時間范圍的松弛過程,模型需要更多的率相關單元進行描述,也就導致更多的模型參數.同樣,遺傳積分法模型適用的應變率范圍往往由模型中松弛模量函數覆蓋的時間范圍決定,對于采用Prony 級數形式松弛函數的模型,模型參數會較多.應變?時間解耦法模型的應變率范圍取決于研究者對時間相關項的構造.

對于溫度敏感性,從表1 可以看出變形梯度乘法分解框架建立的模型較少考慮聚脲的溫度敏感性,而遺傳積分法建模方式往往涉及到材料寬范圍的松弛模量,以及實驗上獲取寬時間范圍松弛模量涉及到的時溫等效原理,因此遺傳積分法對聚脲溫度敏感性的考慮具有天然的優勢.應變?時間解耦法通常只考慮了應變率效應,是否有相應的應變?時間?溫度解耦有待研究人員進一步深入探討.

表1 各模型對比Table 1 Comparison of all models

此外,壓力相關性的考慮往往取決于研究人員關注的問題是否涉及到高靜水壓,如Jiao 模型[53]、Amirkhizi-Nemat-Nasser 模型[15]均被用于壓剪板沖擊實驗的模擬.聚脲的軟化行為較少被研究者考慮,對其有考慮的主要是變形梯度乘法分解框架中運用Arruda-Boyce 八鏈模型的相關本構模型.Das-Roy 模型運用構型溫度的概念,對壓力相關性、軟化行為等均有考慮,但模型復雜且參數眾多.

3 結語與展望

本文從小變形線性黏彈性和大變形非線性黏彈性兩個方面討論了聚脲的力學性能,同時根據不同的建模方式(包括變形梯度乘法分解法、遺傳積分法、應變?時間解耦法等)綜述了聚脲的本構模型.盡管針對聚脲力學性能,目前已有許多相關的實驗和理論研究,但由于聚脲微結構和力學行為的復雜性,已開展實驗測試手段的相對單一,使得我們對聚脲宏微觀變形與失效行為的認識仍存在一定的局限性,相關理論描述有待進一步發展完善.針對聚脲力學性能與本構關系下一步研究須重點關注的若干問題如下.

(1)目前對聚脲大變形力學行為的研究多集中在簡單加載方式,通過各向同性假定和各向同性強化假定推算復雜加載情況下的力學行為.而已有微結構的研究表明聚脲硬疇的取向會隨著變形發生重排[32,84-85],即聚脲的變形會導致各向異性的出現.因此,聚脲微結構隨變形的演化,以及這些演化對宏觀力學行為和沖擊耗能等的影響需要進一步通過復雜加載測試手段(尤其是高應變率下的復雜加載,如多軸霍普金森桿加載[86]),結合微結構表征實驗進行研究.

(2)聚脲是一種溫度敏感材料,且其應用場景多為高速加載,往往伴隨著黏性、塑性功轉化為熱量,導致材料溫度的升高,這也是影響聚脲變形耗能的重要因素之一.而目前研究者較少從實驗上定量研究聚脲變形與溫升的關系,因此需要建立針對高聚物高速變形過程的溫度測量手段,結合實驗和理論厘清聚脲變形過程中的功熱轉換關系.

(3)研究者雖針對聚脲建立了多種不同形式的本構模型,但模型在適用范圍(未全面考慮聚脲的力學特性)或實用性(參數過多)等方面仍有待進一步發展完善.同時,高應變率加載下聚脲發生橡膠態向玻璃態的轉變,這一轉變的微介觀機理是什么？其與聚脲的宏觀應力應變響應、能量吸收性能等的內在關聯如何？均是尚待解決的重要問題.如何從微觀物理層次出發,構建聚脲的微相分離及其演化與宏觀力學行為的定量關聯,建立對聚脲復雜宏觀力學行為的理論描述,值得進一步深入研究.

(4)已有研究較多關注聚脲應力?應變關系,對聚脲失效行為研究較少.而聚脲在防彈等強沖擊作用下往往涉及到材料的失效破壞,材料的失效破壞又與其耗能行為密切相關.因此,闡明應變率對失效行為的影響,進而建立有效的聚脲失效準則非常有必要.