淺談流體力學(xué)發(fā)展
——從Batchelor 百年誕辰紀(jì)念大會(huì)談起1)

朱偉 王國華

(蘭州大學(xué)湍流-顆粒研究中心,蘭州 730000)

引言

為了紀(jì)念流體力學(xué)界極具傳奇色彩的大師George Keith Batchelor 誕辰100 周年,劍橋大學(xué)應(yīng)用數(shù)學(xué)與理論物理系(DAMTP)舉辦了主題為“Batchelor精神下的流體力學(xué)”的紀(jì)念大會(huì).會(huì)議從2019 年開始籌備,2021 年3 月29—31 日舉行,受到國際理論與應(yīng)用力學(xué)聯(lián)盟(IUTAM) 和歐洲力學(xué)學(xué)會(huì)(EUROMECH)的資助和高度重視,邀請了包括3 位Batchelor 獎(jiǎng)獲得者在內(nèi)的共6 位在當(dāng)代流體力學(xué)研究非常活躍的前沿領(lǐng)域?qū)W者各自介紹其所在領(lǐng)域的研究成果和進(jìn)展,中國的鄭曉靜教授是亞太地區(qū)唯一一位受邀的大會(huì)報(bào)告人.作為大會(huì)的組織者之一,IUTAM 前主席、Batchelor 的學(xué)生、流體力學(xué)家Keith Moffatt 教授為大會(huì)手冊設(shè)計(jì)了一張封面(圖1),列出了近300 年為流體力學(xué)發(fā)展做出杰出貢獻(xiàn)的150 位學(xué)者.這150 位學(xué)者中有115 位男性、35 位女性,已故學(xué)者34 位,仍在世的學(xué)者116 位;從國籍看包括英國及英聯(lián)邦國家學(xué)者58 位,北美(美國、加拿大)學(xué)者45 位,歐盟國家學(xué)者27 位,俄羅斯學(xué)者13 位,亞洲學(xué)者7 位分別是3 位印度學(xué)者、2 位日本學(xué)者和2 位中國學(xué)者.其中包括理論流體動(dòng)力學(xué)的奠基人歐拉(Leonhard Euler),首次導(dǎo)出黏性流體運(yùn)動(dòng)基本方程的納維(Claude-Louis Navier)和斯托克斯(George Gabriel Stokes);在流體力學(xué)理論體系中開宗立派的大師普朗特(Ludvig Prandtl)、泰勒(Geoffrey Ingram Taylor)、馮·卡門(Theodore von Karman)、柯爾莫哥洛夫(Andrey Nikolaevich Kolmogorov),來自中國的世界流體力學(xué)巨人周培源先生,以及在當(dāng)代流體力學(xué)諸多分支的代表性學(xué)者,如地球環(huán)境流體動(dòng)力學(xué)的先驅(qū)Stewart Turner,計(jì)算流體力學(xué)的奠基人Brain Spalding 等等.整個(gè)封面可謂“群星璀璨”,每一位學(xué)者的代表性工作都是流體力學(xué)發(fā)展長河中的一顆珍珠,它們一起勾勒出從經(jīng)典到近現(xiàn)代流體力學(xué)的發(fā)展譜線.

圖1 “Batchelor 精神下的流體力學(xué)”紀(jì)念大會(huì)手冊封面(由Keith Moffatt 教授設(shè)計(jì)并提供)Fig.1 The notebook cover of the Batchelor’s Centennial Symposium “Fluid Mechanics in the Spirit of G.K.Batchelor” (designed and provided by Prof.Keith Moffatt)

本文將圍繞Batchelor 誕辰100 周年紀(jì)念大會(huì)封面對流體力學(xué)近300 年的發(fā)展進(jìn)行簡要回顧.第1 部分將簡要介紹Batchelor 生平及學(xué)術(shù)貢獻(xiàn);第2 部分將回顧經(jīng)典流體力學(xué)到近代流體力學(xué)階段標(biāo)志性的學(xué)術(shù)成就及其影響;第3 部分介紹現(xiàn)代流體力學(xué)流派特點(diǎn)及其傳承;第4 部分以環(huán)境流體力學(xué)的發(fā)展為例,淺談流體動(dòng)力學(xué)理論發(fā)展與應(yīng)用需求的結(jié)合,研究手段的更替以及發(fā)展趨勢;最后是對未來的思考和展望.

1 Batchelor 生平及學(xué)術(shù)貢獻(xiàn)概要

1.1 Batchelor 生平簡介

1920 年3 月8 日,Batchelor (圖2)出生于澳大利亞墨爾本,17 歲時(shí)以高分被墨爾本大學(xué)錄取,并于1941 年獲得了數(shù)學(xué)和物理雙學(xué)士學(xué)位.由于二戰(zhàn)的原因,從大學(xué)畢業(yè)的Batchelor 加入墨爾本(Commonwealth Scientific and Industrial Research,CSIR) 航空部從事與戰(zhàn)爭有關(guān)的航空課題研究,期間對湍流研究特別是當(dāng)時(shí)流體力學(xué)大師泰勒(G.I.Taylor)在1930 年代提出的湍流統(tǒng)計(jì)理論產(chǎn)生了濃厚的興趣.1945 年1 月,Batchelor 前往英國劍橋大學(xué)卡文迪許實(shí)驗(yàn)室跟隨泰勒從事湍流問題的研究,1947 年他便當(dāng)選為劍橋三一學(xué)院研究員(Fellow),后歷任劍橋大學(xué)流體力學(xué)副教授(1948—1959),應(yīng)用數(shù)學(xué)理論物理系主任(1959—1983),應(yīng)用數(shù)學(xué)教授(1964—1983),榮譽(yù)教授(1984—2000).1956 年,Batchelor 創(chuàng)辦了流體力學(xué)頂級期刊Journal of Fluid Mechanics(JFM)并擔(dān)任其首任主編40 余年;1959年創(chuàng)建了劍橋大學(xué)應(yīng)用數(shù)學(xué)與理論物理系(Department of Applied Mathematics and Theoretical Physics,DAMTP)并擔(dān)任系主任至1986 年;倡導(dǎo)成立了歐洲力學(xué)聯(lián)盟(EUROMECH)并擔(dān)任第一任主席.他是英國劍橋大學(xué)Adams 獎(jiǎng)(1951)、意大利Agostinelli獎(jiǎng)(1986)、英國皇家學(xué)會(huì)獎(jiǎng)?wù)?1988)、美國機(jī)械工程師協(xié)會(huì)Timoshenko 獎(jiǎng)?wù)?1988)等獎(jiǎng)項(xiàng)的獲得者.此外,Batchelor 還先后當(dāng)選為倫敦皇家學(xué)會(huì)(1959)、美國藝術(shù)與科學(xué)院(1959)、波蘭科學(xué)院(1974)、法國科學(xué)院(1984)和澳大利亞科學(xué)院(1989)等眾多學(xué)會(huì)與國家科學(xué)院院士.

1.2 Batchelor 學(xué)術(shù)貢獻(xiàn)概要

Batchelor 的研究工作主要集中在1945—1960年間,其學(xué)術(shù)貢獻(xiàn)主要涉及到兩個(gè)領(lǐng)域: 湍流和低Reynolds 數(shù)的微流體力學(xué)(也被稱為懸浮力學(xué)).

在湍流研究領(lǐng)域Batchelor 的貢獻(xiàn)包括: 對Kolmogorov 局部各向同性湍流理論(又稱K41 理論)的解釋和推廣、均勻湍流衰減、快速畸變和湍流擴(kuò)散理論.在K41 理論的解釋和推廣方面,Batchelor 最早發(fā)現(xiàn)并意識到K41 理論的重要科學(xué)意義,對其中的假設(shè)和猜想進(jìn)行嚴(yán)格論證,并賦予清晰的物理解釋.1947 年,Batchelor[2]發(fā)表長文向西方世界介紹Kolmogrov,Sedov 等蘇聯(lián)學(xué)者的湍流研究工作,重新推導(dǎo)了各向同性湍流3 階結(jié)構(gòu)函數(shù),被Uriel Frisch 評價(jià)為湍流動(dòng)力理論中唯一精確且非平凡的結(jié)果[3].此外,他還進(jìn)一步挖掘Kolmogrov 隨機(jī)場理論的內(nèi)涵以及推廣,包括將其應(yīng)用于非對稱湍流、時(shí)滯相關(guān)、湍流擴(kuò)散等問題中.在均勻湍流衰減問題方面,Batchelor 和Alan Townsend 一起對均勻湍流衰減率進(jìn)行了研究,指出各向同性湍流中均方渦度的變化率與平均渦度立方成正比,而平均渦度的立方與湍流速度導(dǎo)數(shù)的偏度因子有關(guān),并發(fā)現(xiàn)均勻湍流衰減過程中,黏性耗散衰減占主導(dǎo),非線性效應(yīng)占次要地位,隨著雷諾數(shù)增加二者的貢獻(xiàn)能達(dá)到相當(dāng);在“衰減的最后階段”非線性效應(yīng)變得可以忽略,此時(shí)所有尺度的渦通過直接黏性耗散衰減[4-6].在快速畸變理論方面,Batchelor 繼承了他的導(dǎo)師泰勒對此問題的思考,通過對湍流場的所有傅里葉分量進(jìn)行積分,確定了在初始各向同性湍流場中誘導(dǎo)各向異性的方式,指出如果畸變尺度遠(yuǎn)大于湍流漩渦的時(shí)間尺度,線性處理是合理的[7].這一認(rèn)識以及線性處理明顯優(yōu)于完全不處理的事實(shí)促進(jìn)了快速畸變理論的許多后續(xù)發(fā)展和在廣泛環(huán)境中的應(yīng)用.在湍流擴(kuò)散理論方面,Batchelor 推導(dǎo)了有限體積內(nèi)顆粒的平均濃度滿足的擴(kuò)散方程,建立了兩個(gè)粒子的相對擴(kuò)散與Richardson 擴(kuò)散定律的理論聯(lián)系,提出了Batchelor 尺度,奠定了被動(dòng)標(biāo)量輸運(yùn)問題的研究基礎(chǔ)[8].

在低Reynolds 數(shù)的微流體力學(xué)領(lǐng)域,Batchelor發(fā)現(xiàn)了愛因斯坦在推導(dǎo)小顆粒擴(kuò)散的有效黏度時(shí)的漏洞,即,沒有計(jì)算由于一個(gè)粒子的存在而產(chǎn)生的總附加耗散的體積積分,而是使用了另一個(gè)類似的非絕對收斂積分.在1972 年的文章“Sedimentation in a dilute dispersion of spheres”[9]中Batchelor 借用湍流理論的思想,通過更嚴(yán)謹(jǐn)?shù)姆绞浇o出了小顆粒在黏性流體中的擴(kuò)散以及擴(kuò)散的有效黏度的數(shù)學(xué)推導(dǎo).由于小顆粒擴(kuò)散與氣溶膠、沉降、布朗運(yùn)動(dòng)、流變學(xué)和復(fù)合材料等學(xué)科都有密切關(guān)聯(lián),Batchelor 在這一領(lǐng)域的開創(chuàng)性工作引領(lǐng)了后續(xù)許多學(xué)者一起參與到這個(gè)領(lǐng)域的研究中.

在Batchelor 的學(xué)術(shù)研究過程中,他形成了以物理的洞察力為基礎(chǔ),將物理思想注入數(shù)學(xué)之中,根據(jù)問題的特點(diǎn)建立模型并提出或者引入簡化、近似方案的方法論與研究風(fēng)格.1953 年,Batchelor 獨(dú)立完成了湍流專著The Theory of Homogenous Turbulence[10],系統(tǒng)地總結(jié)了他和在他之前湍流理論的主要進(jìn)展,是湍流領(lǐng)域影響深遠(yuǎn)的著作.而由他編寫的流體力學(xué)的理論專著An Introduction to Fluid Dynamics[11]也將這種思想和方法論貫穿始終,成為流體力學(xué)的傳世佳作.期間許多研究成果被后人以Batchelor 的名字命名,例如Batchelor 渦、Prandtl-Batchelor 定理、Batchelor-Chandrasekhar 公式、Batchelor 尺度等,至今仍是湍流研究領(lǐng)域中熱議的話題.

2000 年3 月30 日,Batchelor 逝世.為了紀(jì)念他,2007 年國際理論與應(yīng)用力學(xué)聯(lián)盟(IUTAM)設(shè)立了The Batchelor Prize in Fluid Mechanics.該獎(jiǎng)項(xiàng)被譽(yù)為流體力學(xué)界的“諾貝爾獎(jiǎng)”,每4 年評選一次,是流體力學(xué)的最高榮譽(yù)之一.

2 流體力學(xué)發(fā)展回顧

圖1 列舉的150 位流體力學(xué)家橫跨了近300 年,歷經(jīng)流體力學(xué)發(fā)展的3 個(gè)階段: 經(jīng)典流體力學(xué)(17 世紀(jì)中葉至19 世紀(jì)末)、近代流體力學(xué)(19 世紀(jì)末至20 世紀(jì)中葉) 和現(xiàn)代流體力學(xué)(20 世紀(jì)中葉至今),所涉及的領(lǐng)域包括流體動(dòng)力學(xué)理論、實(shí)驗(yàn)流體力學(xué)、計(jì)算流體力學(xué)、湍流及穩(wěn)定性、空氣動(dòng)力學(xué)、環(huán)境流體力學(xué)、多相流體力學(xué)、生物流體力學(xué)、磁流體力學(xué)、微納米尺度流體動(dòng)力學(xué)等.以下將結(jié)合學(xué)者與他們對流體力學(xué)的主要貢獻(xiàn),回顧流體力學(xué)的發(fā)展歷程.

2.1 經(jīng)典流體力學(xué)階段

經(jīng)典流體力學(xué)階段始于力、速度、加速度、流場等經(jīng)典力學(xué)概念的建立以及質(zhì)量、動(dòng)量、能量三大守恒定律的誕生,時(shí)間上大致處于17 世紀(jì)中葉至19 世紀(jì)末之間.150 人的名單中有8 位處于經(jīng)典流體力學(xué)階段的學(xué)者,他們分別是歐拉(L.Euler)、納維(C.L.Navier)、泊肅葉(Jean-Louis-Marie Poiseuille)、弗勞德(William Froude)、斯托克斯(G.G.Stokes)、麥克斯韋爾(James Clerk Maxwell)、瑞利(Lord Rayleigh)和索菲?柯瓦列夫斯卡婭(Sofia Kovalevskaya),他們在流體力學(xué)領(lǐng)域作出的主要成就見表1.Kelvin 勛爵(William Thomson)評價(jià)這一時(shí)期的流體力學(xué)是“所有物理科學(xué)的根本,并且具有首屈一指的數(shù)學(xué)之美”[12].一方面這一時(shí)期數(shù)學(xué)分析方法包括微積分、微分方程等的建立和應(yīng)用為流體力學(xué)基本理論框架奠定了牢固的基礎(chǔ),另一方面當(dāng)時(shí)科學(xué)和技術(shù)的前沿研究對象大都繞不開流體力學(xué)的基本問題,而后者在數(shù)學(xué)描述上的成功也使得這一學(xué)科首先得到了蓬勃的發(fā)展.

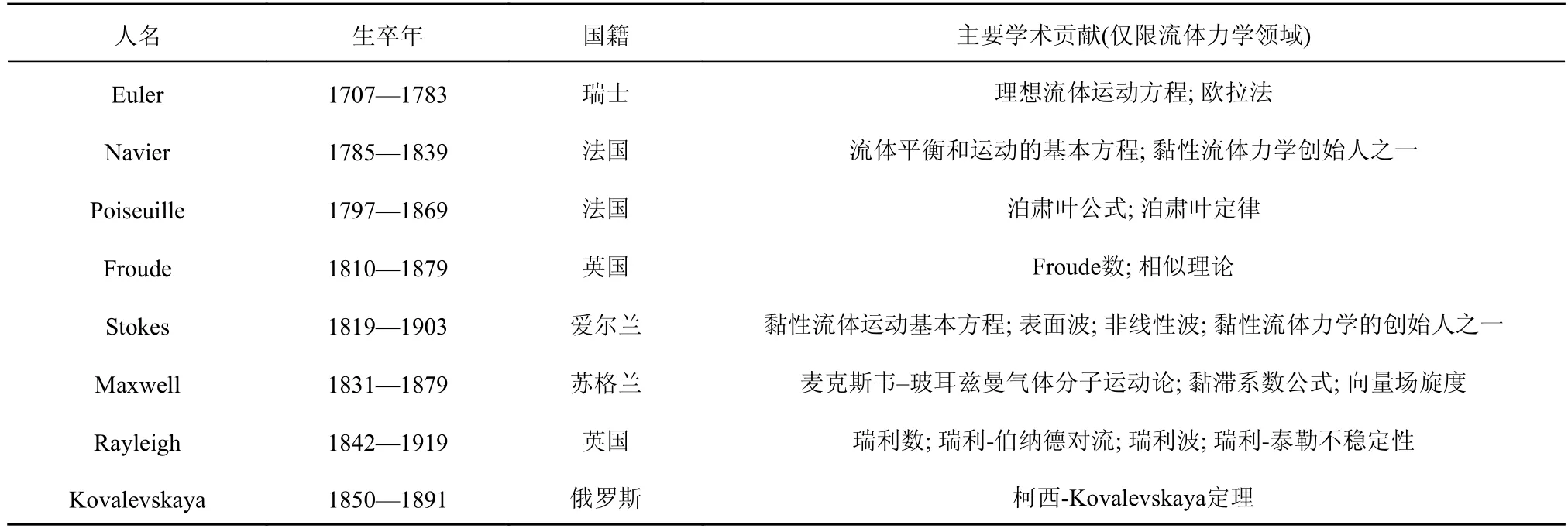
表1 圖1 中處于經(jīng)典流體力學(xué)階段的學(xué)者信息[13]Table 1 Information and contributions of the fluid dynamicists in the stage of classical fluid mechanics listed in Fig.1[13]

1665 年,牛頓(Isaac Newton)發(fā)現(xiàn)了微積分,在他的著作《數(shù)學(xué)原理》中研究了流體中運(yùn)動(dòng)物體受到的阻力,認(rèn)為黏性切應(yīng)力是流體黏度與速度梯度的乘積,提出了牛頓黏性定律.1738 年伯努利(Daniel Bernaulli)證明了“壓力梯度與流體的加速度成正比”提出了“伯努利方程(原理)”.1752 年,歐拉提出理想流體概念,并基于連續(xù)介質(zhì)(流體微團(tuán))假設(shè)和牛頓第二定律給出了描述理想流體運(yùn)動(dòng)的基本方程——?dú)W拉方程.這是第一個(gè)將微分方程應(yīng)用到流體力學(xué)領(lǐng)域的方程,同時(shí)也奠定了流體力學(xué)流場描述的標(biāo)準(zhǔn)形式.歐拉方程與牛頓黏性定律、伯努利原理一起構(gòu)成了經(jīng)典流體動(dòng)力學(xué)大廈的3 塊基石.從這3 位奠基人都兼具數(shù)學(xué)家身份這一點(diǎn)可以看出,經(jīng)典流體動(dòng)力學(xué)對現(xiàn)象的研究和理解都是建立在嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)基礎(chǔ)之上的,而對物理現(xiàn)象的數(shù)學(xué)處理也通過經(jīng)典流體動(dòng)力學(xué)的發(fā)展達(dá)到了登峰造極的地步.

同樣是基于嚴(yán)格的數(shù)學(xué)推導(dǎo),1752 年達(dá)朗貝爾(Jean le Rond d'Alembert)從歐拉方程出發(fā)得到了“達(dá)朗貝爾佯謬”,即: 不可壓縮、無黏勢流中勻速運(yùn)動(dòng)的物體不受力.這一結(jié)論意味著以相對于流體以恒定速度運(yùn)動(dòng)的物體受到的拖曳力為0.這與實(shí)驗(yàn)觀測和工程實(shí)際中觀察到的相對于流體(空氣和水)勻速移動(dòng)的物體受到阻力作用的現(xiàn)象有著尖銳的矛盾.

為了尋求達(dá)朗貝爾悖論的解答,19 世紀(jì)眾多流體力學(xué)家和應(yīng)用數(shù)學(xué)家針對物體在黏性流體中運(yùn)動(dòng)受到的阻力進(jìn)行建模,并將其引入流體動(dòng)力學(xué)基本方程.當(dāng)時(shí)流體力學(xué)界的普遍觀點(diǎn)認(rèn)為造成達(dá)朗貝爾悖論的主要原因是歐拉方程不考慮流體的內(nèi)摩擦,即黏性對流體運(yùn)動(dòng)的影響,只要在歐拉方程中增加一個(gè)摩擦項(xiàng)便能彌補(bǔ)理論與實(shí)踐的不符.1822 年,法國工程師納維基于分子機(jī)制的摩擦在歐拉方程的基礎(chǔ)上加入一個(gè)額外項(xiàng),建立了黏性不可壓縮流體動(dòng)量守恒的運(yùn)動(dòng)方程;隨后柯西(1828)、泊松(1829)和圣維南(1943)等也對黏性機(jī)制進(jìn)行了研究;1840 年,泊肅葉發(fā)表《小管徑內(nèi)液體流動(dòng)的實(shí)驗(yàn)研究》,通過實(shí)驗(yàn)得到了圓管中黏性流體的流量公式——泊肅葉公式(定律),后世將也黏性流體在管道中的流動(dòng)稱為泊肅葉流動(dòng)[14].在此基礎(chǔ)上,1845 年,劍橋?qū)W者斯托克斯以更合理嚴(yán)謹(jǐn)?shù)姆绞綄?dǎo)出了黏性流體運(yùn)動(dòng)方程,開啟了黏性流體運(yùn)動(dòng)理論.這組方程就是沿用至今的納維?斯托克斯方程(簡稱N-S 方程).N-S 方程一經(jīng)建立便被公認(rèn)為是黏性流體運(yùn)動(dòng)理論的第一原理,它與描述電磁場的麥克斯韋爾方程、彈性介質(zhì)的柯西方程一同成為19 世紀(jì)三大最著名的偏微分方程(組),是當(dāng)時(shí)數(shù)學(xué)、物理、力學(xué)理論研究的前沿課題.1870 年,俄羅斯女?dāng)?shù)學(xué)家柯瓦列夫斯卡婭完成了柯西-柯瓦列夫斯卡婭定理的證明,該定理作為偏微分方程理論中第一個(gè)普遍性解的存在定理,保證了上述幾類偏微分方程解的存在性.此后,諸多科學(xué)和工程問題得以建立在N-S 方程的基礎(chǔ)上進(jìn)行定量揭示和描述.然而,基于力學(xué)觀點(diǎn)增加的對流項(xiàng)卻成為N-S 方程的非線性項(xiàng),處理非線性問題數(shù)學(xué)上的困難一定程度上也限制了黏性流體力學(xué)的全面發(fā)展.

除了黏性流體力學(xué)的發(fā)展,19 世紀(jì)流體力學(xué)的主要進(jìn)展還包括非線性波動(dòng)、旋渦運(yùn)動(dòng)和流動(dòng)不穩(wěn)定性方面的研究.非線性水波方面,1834 年羅素觀察到了孤立波的存在,1847 年斯托克斯建立了非線性水波理論.1869 年,蘭金給出了激波前后的關(guān)系式,這是對流動(dòng)可壓縮性的初步研究結(jié)果[15];旋渦運(yùn)動(dòng)方面,1857 年亥姆霍茲發(fā)表了“論描述渦旋運(yùn)動(dòng)的流體動(dòng)力學(xué)方程之積分”,糾正了流動(dòng)只能是勢流的錯(cuò)誤觀點(diǎn),首次研究了有旋流動(dòng)并建立了3 個(gè)渦定理,開創(chuàng)了渦旋動(dòng)力學(xué)的研究;流動(dòng)不穩(wěn)定性方面,1880 年瑞利(Lord Rayleigh)對平行剪切流的不穩(wěn)定性(瑞利-泰勒不穩(wěn)定性)進(jìn)行了開創(chuàng)性研究,提出了“瑞利方程”.他在研究上下溫差引起的對流(瑞利?伯納德對流)時(shí)引入了一個(gè)描述浮力驅(qū)動(dòng)對流的無量綱數(shù)(瑞利數(shù)),一直被沿用于解釋由于地面?大氣對流引起的現(xiàn)象.此外,他對超聲速氣流的雙曲型方程數(shù)學(xué)理論方面也做出了奠基性的貢獻(xiàn).

2.2 近代流體力學(xué)階段

近代流體力學(xué)時(shí)間軸上位于19 世紀(jì)末到20 世紀(jì)中葉.受到第二次工業(yè)革命的影響,這一時(shí)期實(shí)驗(yàn)技術(shù)手段有了巨大的進(jìn)步,誕生了風(fēng)洞、水槽實(shí)驗(yàn)以及熱線等實(shí)驗(yàn)裝置和測量儀器,因此流體力學(xué)的發(fā)展呈現(xiàn)出鮮明的理論與實(shí)驗(yàn)相互促進(jìn)的特點(diǎn),同時(shí)工業(yè)生產(chǎn)的實(shí)際需求也成為這一時(shí)期流體力學(xué)發(fā)展的“催化劑”.近代流體力學(xué)的主要研究對象是湍流和空氣動(dòng)力學(xué),在這兩個(gè)領(lǐng)域中,諸多新概念的提出極具想象力,結(jié)合數(shù)學(xué)推導(dǎo)建立模型并將其應(yīng)用于解釋或揭示新現(xiàn)象及其規(guī)律,是這一時(shí)期的流體力學(xué)研究的風(fēng)格.多位流體力學(xué)開宗立派的大師均誕生于這兩個(gè)領(lǐng)域,各具風(fēng)格和特色鮮明的學(xué)派也于這一時(shí)期開始形成.圖1 列舉的處于這一時(shí)期的學(xué)者對流體力學(xué)發(fā)展的貢獻(xiàn)見表2(摘選自文獻(xiàn)[16]).

表2 圖1 中處于近代流體力學(xué)階段的學(xué)者貢獻(xiàn)[16]Table 2 Major contributions of the fluid dynamicists in the stage of modern fluid mechanics listed in Fig.1[16]

1883 年,雷諾(Osborne Reynolds)通過圓管內(nèi)水流實(shí)驗(yàn)向人們展示了管道中黏性流體從平滑流線型流動(dòng)(層流)向不規(guī)則帶旋渦的流動(dòng)(湍流)的過渡,這是流動(dòng)從層流向湍流轉(zhuǎn)捩的首次實(shí)驗(yàn)展示,此外,雷諾還引入了表征流動(dòng)中流體慣性力和黏性力之比的一個(gè)無量綱數(shù),即雷諾數(shù),作為判別兩種流態(tài)的標(biāo)準(zhǔn).此后,流動(dòng)的雷諾數(shù)成為描述流體流動(dòng)狀態(tài)的關(guān)鍵參數(shù).1895 年,雷諾在N-S 方程的基礎(chǔ)上推導(dǎo)出時(shí)均流動(dòng)的N-S 方程,同時(shí)提出了湍流切應(yīng)力概念.可以說,雷諾的工作開啟了長達(dá)一個(gè)多世紀(jì)湍流研究的序幕.

1904 年,在海德堡舉行的第3 屆國際數(shù)學(xué)家大會(huì)上,德國流體力學(xué)家路德維希·普朗特(Ludvig Prandtl)作了一個(gè)有劃時(shí)代意義的演講“關(guān)于非常小摩擦下的流動(dòng)”[17],從物理直覺出發(fā)提出了邊界層概念,這樣就可以將整個(gè)流動(dòng)分成兩部分來處理,即“滿足壁面附近黏附條件的黏性流動(dòng)解和遠(yuǎn)離壁面處理想流動(dòng)解”.邊界層理論是突破性的,沿著這一思路,達(dá)朗貝爾悖論從實(shí)際應(yīng)用的角度上得到了解決.同時(shí),在邊界層理論框架下,無黏流的理論找到了應(yīng)用范圍,而黏性計(jì)算限制在很薄的邊界層內(nèi),使得N-S 方程得以大大的簡化,很多實(shí)際問題能夠得到解答,黏性理論也得到了一條新的發(fā)展道路.邊界層理論適用于匹配漸近展開推導(dǎo)近似解,為流體力學(xué)中物面摩擦阻力、熱傳導(dǎo)、流動(dòng)分離的計(jì)算奠定了基礎(chǔ),由此開創(chuàng)的奇異攝動(dòng)理論也是20 世紀(jì)應(yīng)用數(shù)學(xué)的重要成就之一.在航空領(lǐng)域,該理論可以直接應(yīng)用于計(jì)算翼型的阻力,為航空工程也里程碑式的貢獻(xiàn).由此,普朗特被認(rèn)為是空氣動(dòng)力學(xué)之父和近代流體力學(xué)奠基人.

1925 年,普朗特仿照氣體分子運(yùn)動(dòng)論提出混合長度理論,用湍渦的混合長度代替分子自由路徑,將湍渦的無規(guī)則脈動(dòng)速度就和平均流場的平均速度梯度聯(lián)系起來,化解了未知的雷諾應(yīng)力,使雷諾方程封閉.雖然混合長度理論將雷諾應(yīng)力化解掉了,但又多出一個(gè)混合長未知數(shù)需要確定.1930 年普朗特的學(xué)生馮·卡門(Theodore von Karman)提出一種相似理論來解決混合長度計(jì)算問題,然而這個(gè)方法比較復(fù)雜.1933 年,普朗特本人又提出一種簡單直觀的方法,即直接假定湍渦的混合長和距離壁面的距離成正比,而該比例系數(shù)只能由實(shí)驗(yàn)確定.因此,普朗特的混合長度理論前面加上了“半經(jīng)驗(yàn)”二字,被稱為“半經(jīng)驗(yàn)混合長度理論”.將半經(jīng)驗(yàn)混合長度理論應(yīng)用到一種最簡單的平面平板流動(dòng)中,就可以推導(dǎo)出著名的平均流場的對數(shù)分布律,而后來的大量實(shí)驗(yàn)也證實(shí)了這種對數(shù)律的存在.隨后,前蘇聯(lián)學(xué)者莫寧(Andrei Sergeevich Monin)和奧本霍夫(Alexander Mikhailovich Obukhov)將混合長度理論成功推廣到大氣邊界層的中風(fēng)速的分布問題中,為解決大氣物理中大氣擴(kuò)散等問題開辟了道路.

同在1920 年代,Batchelor 的老師、劍橋大學(xué)數(shù)學(xué)、力學(xué)家泰勒致力于通過建立能與實(shí)驗(yàn)數(shù)據(jù)直接和定量比較的數(shù)學(xué)理論來描述湍流.在研究湍流擴(kuò)散問題時(shí),泰勒引入了流場中同一點(diǎn)在不同時(shí)刻脈動(dòng)速度的相關(guān)(又稱拉格朗日相關(guān))描述流動(dòng)的擴(kuò)散能力,得到了在時(shí)間間隔小于相關(guān)時(shí)間時(shí)湍流擴(kuò)散的彌散度與時(shí)間的平方成正比,而在時(shí)間間隔遠(yuǎn)大于相關(guān)時(shí)間時(shí),彌散度與時(shí)間的一次方成正比的規(guī)律.1935 年,泰勒又引進(jìn)同一時(shí)刻不同點(diǎn)上速度分量的相關(guān)(又稱歐拉相關(guān)),并提出一種數(shù)學(xué)上容易處理的理想湍流?均勻各向同性湍流,用于簡化脈動(dòng)速度相關(guān)矩方程,以解決雷諾方程的封閉性問題.盡管最終泰勒沒有完成這個(gè)理論,但他利用相關(guān)矩和譜分析等統(tǒng)計(jì)方法處理湍流問題的模式奠定了湍流統(tǒng)計(jì)理論發(fā)展的基礎(chǔ).不僅限于湍流領(lǐng)域,泰勒在低雷諾數(shù)流動(dòng)、流動(dòng)不穩(wěn)定性、渦旋流動(dòng)領(lǐng)域中也作出了諸多開創(chuàng)性的工作,包括闡明了激波內(nèi)部結(jié)構(gòu);得出同軸兩轉(zhuǎn)動(dòng)圓軸間流動(dòng)失穩(wěn)條件,在研究原子彈爆炸中提出強(qiáng)爆炸的自模擬理論;指出在液滴中起主要作用的是表面張力而不是黏性力等.在IUTAM“世紀(jì)之交的力學(xué)”報(bào)告中由IUTAM 大會(huì)委員會(huì)成員及諸位主席推薦的24 篇20 世紀(jì)的“力學(xué)學(xué)科里程碑式論文”中,泰勒的論文就占了4 篇之多.

1938 年,馮·卡門和霍沃思(Leslie Howarth)在泰勒的均勻各向同性概念的基礎(chǔ)上,從N-S 方程出發(fā)得到了空間兩點(diǎn)縱向二階相關(guān)矩方程,即Karman-Howarth (K-H)方程.雖然K-H 方程仍不閉合,但它證明了N-S 方程不僅是支配層流運(yùn)動(dòng)的基本方程,也是支配湍流運(yùn)動(dòng)的基本方程,早期的均勻各向同性相關(guān)理論就是研究這一方程的各種封閉方法和解的形式.在近似條件下,K-H 方程能直接導(dǎo)出湍動(dòng)能衰變的規(guī)律: 前蘇聯(lián)學(xué)者M(jìn)ikhail Dimitrievich Millionshchikov (A.N.Kolmogorov 的博士生)導(dǎo)出了湍流發(fā)展末期的?5/2 次方律;湍流衰減的初期,忽略黏性項(xiàng)的K-H 方程可直接導(dǎo)出?10/7 次方律.結(jié)合泰勒由實(shí)驗(yàn)總結(jié)出的?2 次方衰減律,一起完整的刻畫了湍動(dòng)能衰減規(guī)律.

作為20 世紀(jì)最偉大的航天工程學(xué)家,馮·卡門還是鈍體阻力理論、亞聲速和跨聲速流空氣動(dòng)力學(xué)、超聲速流細(xì)長體理論等的建立者.不得不提的還有他在1943 年《美國應(yīng)用數(shù)學(xué)季刊》創(chuàng)刊號卷首發(fā)表的“用數(shù)學(xué)武裝工程科學(xué)”一文中號召工程師為非線性問題拼搏,預(yù)見到非線性力學(xué)在今后科學(xué)發(fā)展中的重要地位[18],開創(chuàng)了數(shù)學(xué)和基礎(chǔ)科學(xué)在航空航天和其他技術(shù)領(lǐng)域的應(yīng)用.

同在1940 年代,圖1 中的兩位中國籍力學(xué)家之一、中國近代力學(xué)奠基人周培源先生從另一途徑出發(fā),先對N-S 方程求解,再對所得的基元渦進(jìn)行統(tǒng)計(jì)平均來研究均勻各向同性湍流,也得到了相關(guān)量的衰減律.此外,他還引進(jìn)了湍流脈動(dòng)的二階和三階矩方程,首先得到了相關(guān)函數(shù)的微分方程,為現(xiàn)代湍流高階矩模式理論奠定了基礎(chǔ),之后還提出了湍流的旋渦結(jié)構(gòu)模型,其建立的湍流模式理論是CFD 模擬湍流的關(guān)鍵.1995 年,周培源先生在《流體力學(xué)年鑒》(Annual Review of Fluid Mechanics)上發(fā)表了題為“中國湍流研究50 年(50 years of turbulence research in China)”的文章[19],回顧了上述成果.康奈爾大學(xué)教授約翰·拉姆利 (John Lumley)為這篇文章作序稱: “在湍流領(lǐng)域,他(周培源)被認(rèn)為是計(jì)算模式之父.在其發(fā)表于《中國物理雜志》一篇原創(chuàng)文章及以后發(fā)表在國際期刊上更為詳細(xì)的3 篇論文中,他引進(jìn)了湍流脈動(dòng)二階和三階矩的方程……,遺憾的是,周的建議是在計(jì)算機(jī)發(fā)明之前,要靠手來進(jìn)行大量的計(jì)算是很難的.盡管如此,毫無疑問的是,今天全世界數(shù)以百計(jì)正在從事發(fā)展湍流計(jì)算模式,使之可用于CFD 設(shè)計(jì)和規(guī)范的人們,追本溯源都可以算作周1940 年文章的后繼……在這一代人中,在流體力學(xué)中至少有來自不同國家的4 位巨人,他們以自己的方法在國內(nèi)外都產(chǎn)生了很大的影響.既是由于他們對流體力學(xué)的貢獻(xiàn),也是由于他們提供的智慧和指引.在每一個(gè)國家,那些非凡的后繼者,在流體力學(xué)中的出色的工作者,都可以追蹤為這些巨人的學(xué)術(shù)繼承人.我所說的4 位巨人是: 美國的馮·卡門、前蘇聯(lián)的柯爾莫哥洛夫、英國的泰勒和中國的周培源.”

3 現(xiàn)代流體力學(xué)學(xué)派與傳承

從20 世紀(jì)中葉開始,流體力學(xué)進(jìn)入到現(xiàn)代流體力學(xué)階段.圖1 列舉的這一時(shí)期流體力學(xué)學(xué)者主要的學(xué)術(shù)貢獻(xiàn)見表3(摘選自文獻(xiàn)[16]).這一時(shí)期流體力學(xué)發(fā)展形成了風(fēng)格獨(dú)特、特色鮮明的學(xué)派,包括德國的普朗特為代表的“哥廷根學(xué)派”、英國的泰勒為代表的“劍橋?qū)W派”、前蘇聯(lián)的柯爾莫哥洛夫?yàn)榇淼摹澳箍茖W(xué)派”以及美國的馮·卡門為代表的“加州理工學(xué)派”.其中“哥廷根學(xué)派”的研究受到當(dāng)時(shí)德國工業(yè)需求影響,關(guān)注工業(yè)、工程應(yīng)用中的流體力學(xué)問題,提出了混合長度模式,建立了邊界層理論,將理論與航空需求相結(jié)合創(chuàng)立了空氣動(dòng)力學(xué);“劍橋?qū)W派”的研究風(fēng)格是通過小型室內(nèi)實(shí)驗(yàn)了解機(jī)理,挖掘物理本質(zhì),再用應(yīng)用數(shù)學(xué)方法求解問題,研究對象更側(cè)重于自然界中的湍流(如大氣、海洋)問題;“莫斯科學(xué)派”的特點(diǎn)是將純數(shù)學(xué)領(lǐng)域的工作拓展到實(shí)際應(yīng)用中;而馮·卡門離開哥廷根加入美國加州理工大學(xué)后,沿襲了應(yīng)用力學(xué)研究范式,以航空航天工程中的力學(xué)問題為對象,將現(xiàn)代力學(xué)中的數(shù)學(xué)理論和工程實(shí)際緊密結(jié)合,奠定了現(xiàn)代力學(xué)的基本方向,形成了“加州理工學(xué)派”.

表3 圖1 中處于現(xiàn)代流體力學(xué)階段的學(xué)者貢獻(xiàn)[16]Table 3 Major contributions of the fluid dynamicists in the stage of contemporary fluid mechanics listed in Fig.1[16]

3.1 流體力學(xué)的四大學(xué)派

流體力學(xué)“哥廷根學(xué)派”的創(chuàng)始人普朗特一生培養(yǎng)了90 名博士,圖1 中列出了其中3 位對流體力學(xué)作出了突出貢獻(xiàn)的學(xué)者,他們分別是: Theodore von Karman (1881—1963),Hermann Schilichting(1907—1982),Dietrich Küchemann (1911—1976).H.Schilichting 因其對邊界層轉(zhuǎn)捩狀態(tài)的Tollmien-Schilichting 波的研究而聞名,此外,他在黏性效應(yīng)的流體流動(dòng)和翼型空氣動(dòng)力學(xué)方面也有突出貢獻(xiàn),著有《邊界層理論》[20];D.Küchemann 的工作集中在高速飛行、后掠翼理論方面,第一款商用超音速飛機(jī)“協(xié)和飛機(jī)”采用的就是由他設(shè)計(jì)的“Küchemann Coke Bottle”外形,此外,他設(shè)計(jì)的飛機(jī)后緣防震體被稱為“Küchemann Carrot”.

“劍橋?qū)W派”的創(chuàng)始人泰勒培養(yǎng)了15 名博士,除了第1 節(jié)中介紹過的Batchelor 外,圖1 中還列出了5 位,他們分別是: Alan Townsend (1917—2010),Stewart Turner (1930—),Owen Phillips (1930—2010),Philip Drazin (1934—2002),Francis Bretherton(1935—2021).Townsend 除了通過實(shí)驗(yàn)測量與Batchelor 一起揭示了湍流大尺度渦的間歇性外,他還是湍流擬序結(jié)構(gòu)研究早期的開創(chuàng)者,Townsend 附著渦、Batchelor-Howell-Townsend 譜以及Townsend-Perry 常數(shù)均以他的名字命名,代表性著作The Structure of Turbulent Shear Flow[21].S.Turner 是地球物理流體動(dòng)力學(xué)的奠基人,在分層流和重力流中的湍流輸運(yùn)、海洋中的混合層動(dòng)力學(xué)、浮力羽流和熱氣流、室內(nèi)通風(fēng)流動(dòng)動(dòng)力學(xué)、雙擴(kuò)散對流等領(lǐng)域均作出了開創(chuàng)性的研究工作,1969 年和1974 年分別就浮力羽流和熱氣流、雙擴(kuò)散對流問題在《流體力學(xué)年鑒》上發(fā)表了2 篇綜述[22-23].O.Phillips 的代表性工作是大氣渦旋引發(fā)的海浪,即Phillips-Miles 過程,以及海浪能量傳輸模型,著有The Dynamics of the Upper Ocean[24].P.Drazin 致力于水動(dòng)力穩(wěn)定性問題的研究,提出N-S 方程全局模態(tài)解的概念,將非線性動(dòng)力系統(tǒng)概念引入流體力學(xué)研究.F.Bretherton 則是弱非線性波擴(kuò)散方程的建立者,波-平均流相互作用和大氣鋒生研究的開創(chuàng)性先驅(qū),此外還領(lǐng)導(dǎo)了美國氣象學(xué)會(huì)的全球氣候變化研究項(xiàng)目.

此外,150 人中還包括4 位Batchelor 培養(yǎng)的博士: Brue Morton (1926—2012),Ian Proudman (1927—1999),Phillip Saffman (1931—2008)以及Adrian Gill(1937—1986).B.Morton 在煙囪、火焰流動(dòng),橋梁與飛機(jī)周圍的氣流以及渦度等方面作出了諸多成就;I.Proudman 致力于剪切流動(dòng)穩(wěn)定性以及各向同性湍流統(tǒng)計(jì)理論的深入研究;P.Saffman 的研究生涯成果豐碩,包括Saffman-Taylor 不穩(wěn)定性、船舶與飛機(jī)在水和空氣中運(yùn)動(dòng)產(chǎn)生的渦度理論、尾流湍流、流體中球形顆粒的運(yùn)動(dòng)等方面均有卓越建樹,著有渦動(dòng)力學(xué)經(jīng)典著作Vortex Dynamics[25];A.Gill 則是氣象學(xué)和海洋學(xué)的著名學(xué)者,在管道流動(dòng)穩(wěn)定性、熱對流、南大洋環(huán)流、海洋的季節(jié)變化、旋轉(zhuǎn)流體中的波浪、風(fēng)引起的上升流以及海岸流和海平面變化等領(lǐng)域均作出了理論貢獻(xiàn),著有教材Atmosphere-Ocean Dynamics[26].此外,圖1 的設(shè)計(jì)者K.Moffatt也是Batchelor 的學(xué)生,他是當(dāng)代湍流理論和磁流體動(dòng)力學(xué)領(lǐng)域公認(rèn)的大家.

“莫斯科學(xué)派”創(chuàng)始人柯爾莫哥洛夫一生培養(yǎng)了82 名學(xué)生,圖1 列舉了其中6 位投身于流體力學(xué)領(lǐng)域的學(xué)者: M.Millionshchikov (1913—1973),A.Obukhov (1918—1989),Akiva Yaglom (1921—2007),A.S.Monin (1921—2007),Grigory Isaakovich Barenblatt (1927—2018)以及Vladimir Igorevich Arnold (1937—2010).M.Millionshchikov 在湍流理論方面提出了準(zhǔn)正規(guī)封閉模式,在應(yīng)用方面建立了應(yīng)用氣體動(dòng)力學(xué)理論,提出了油氣開采的新方法,并為前蘇聯(lián)軍事工業(yè)包括氣體噴射器和核工業(yè)的發(fā)展作出了奠基性工作;A.Obukhov 是大氣物理學(xué)和現(xiàn)代邊界層氣象學(xué)的奠基人之一,M-O 相似理論的提出者;A.Yaglom 建立了均勻各向同性、黏性可壓縮湍流理論,導(dǎo)出了湍流溫度場的動(dòng)力學(xué)方程,是繼柯爾莫哥洛夫速度場動(dòng)力學(xué)方程之后湍流理論中的第二個(gè)精確結(jié)果;A.S.Monin 是M-O 相似理論的另一位作者,領(lǐng)導(dǎo)了前蘇聯(lián)在海洋湍流方面的研究,A.S.Monin 和A.Yaglom 合著的Statistical Fluid Mechanics卷1 和卷2[27]是湍流統(tǒng)計(jì)理論的經(jīng)典著作;G.I.Barenblatt 建立了湍流中重顆粒傳輸?shù)臄?shù)學(xué)模型,中間漸近與不完全相似性方法,穩(wěn)定分層湍流中湍斑動(dòng)力學(xué)、非穩(wěn)態(tài)傳熱和傳質(zhì)、溫度階躍形成的數(shù)學(xué)模型,層間湍流演化的數(shù)學(xué)模型,湍流切變的比例定律以及沙塵暴、熱帶颶風(fēng)的數(shù)學(xué)模型等;V.I.Arnold 是可積系統(tǒng)穩(wěn)定性KAM 定理的3 位作者之一,在流體動(dòng)力學(xué)領(lǐng)域提出奇點(diǎn)理論和ADE 分類問題.

“加州理工學(xué)派”創(chuàng)始人馮·卡門共培養(yǎng)了38 名博士,圖1 只列舉了其中2 位: Hans Liepmann (1914—2009)和林家翹(1916—2013).林家翹先生在流體穩(wěn)定性理論方面用漸近方法獲得了Orr-Sommerfeld 方程的解,發(fā)展了平行流動(dòng)穩(wěn)定性理論,確認(rèn)流動(dòng)失穩(wěn)是引發(fā)湍流的機(jī)理,所得結(jié)果為實(shí)驗(yàn)所證實(shí).他和馮·卡門一起提出了各向同性湍流的湍譜理論,發(fā)展了馮·卡門的相似性理論;H.Liepmann 在流動(dòng)不穩(wěn)定性、湍流剪切流、跨音速流動(dòng)、稀薄氣體流動(dòng)、沖擊波?邊界層相互作用、湍流超音速摩擦、飛機(jī)抖振、磁流體動(dòng)力學(xué)、等離子體物理、液氦流體動(dòng)力學(xué)等領(lǐng)域均有建樹,他的著作《可壓縮流的空氣動(dòng)力學(xué)》[28]和Elements of Gas Dynamics[29]對現(xiàn)代空氣動(dòng)力學(xué)發(fā)展影響深遠(yuǎn).

H.Liepmann 一生任職于加州理工學(xué)院,培養(yǎng)了55 名博士,圖1 中有5 位師承于他的學(xué)者,分別是:Stanley Corrsin (1920—1986),John Laufer (1921—1983),Donald Coles (1924—2013),Satish Dhawan(1920—2002),Roddam Narasimaha (1933—2020).S.Corrsin 因其在被動(dòng)標(biāo)量湍流統(tǒng)計(jì)理論和外區(qū)間歇性方面的工作而聞名,此外他在湍流混合、湍流-非湍流界面以及生物流體力學(xué)方面也都作出了杰出的貢獻(xiàn);J.Laufer 在槽道湍流、湍流混合層以及各向同性湍流方面的工作至今仍被頻繁引用;D.Coles 因其在流動(dòng)實(shí)驗(yàn)裝置設(shè)計(jì)與制造方面而聞名,是壁湍流尾流律的發(fā)現(xiàn)者,也是最早將群論用于流體力學(xué)研究的學(xué)者之一;S.Dhawan 是最早獲得表面摩擦阻力直接測量結(jié)果的學(xué)者,他是印度實(shí)驗(yàn)流體動(dòng)力學(xué)研究之父,建立了印度首個(gè)高速空氣動(dòng)力學(xué)和邊界層實(shí)驗(yàn)室,領(lǐng)導(dǎo)了印度空間計(jì)劃;R.Narasimaha 在湍流降噪、激波結(jié)構(gòu)、湍流尾流和混合流方面成績斐然,他還領(lǐng)導(dǎo)了印度的并行計(jì)算流體動(dòng)力學(xué)研究計(jì)劃、開發(fā)了印度第一套天氣預(yù)報(bào)代碼,參與設(shè)計(jì)了印度輕型戰(zhàn)斗機(jī)等.此外,圖1 中還有幾位馮·卡門第3 代甚至第4 代的學(xué)生,包括師承于S.Corrsin的John Lumley (1930—2015)及J.Lumley 的學(xué)生Nadine Aubry 和Emily Stone;師承于R.Narasimha的Rama Govindarajan 等.可以說,“加州理工學(xué)派”為戰(zhàn)后流體力學(xué)研究在美國的發(fā)展源源不斷的輸送著養(yǎng)分,使之迅速成為引領(lǐng)流體力學(xué)研究發(fā)展的中心之一.

3.2 其他分支

開放交流的發(fā)展模式才能讓學(xué)科青春永駐,現(xiàn)代流體力學(xué)的發(fā)展亦是如此.除了有清晰師承關(guān)系的學(xué)者外,圖1 列舉的現(xiàn)代流體力學(xué)者還呈現(xiàn)出百花齊放之勢,他們?yōu)楝F(xiàn)代流體力學(xué)發(fā)展作出的貢獻(xiàn)同樣值得銘記.

首先是現(xiàn)代流體力學(xué)圣地之一的劍橋大學(xué).圖1中的Harold Jefferys (1891—1989)是一位統(tǒng)計(jì)學(xué)家,在與其同時(shí)期的泰勒交流中他對海浪的生成、海嘯的形成產(chǎn)生興趣,并進(jìn)行了大量深入的研究,他培養(yǎng)的學(xué)生Longuet-Higgins (1925—2016)在海浪、洋流和自然現(xiàn)象的數(shù)學(xué)模型上做出了杰出的貢獻(xiàn);他的另一位學(xué)生Sydney Goldstein (1903—1989)則因在穩(wěn)定層流邊界層方程和流體中圓盤旋轉(zhuǎn)的湍流阻力方面的工作被譽(yù)為“20 世紀(jì)對流體動(dòng)力學(xué)的進(jìn)步影響最大的人之一”[30].此外,與Batchelor 同時(shí)代的Fritz Ursell (1923—2012)和Milton Van Dyke (1922—2010)經(jīng)常參加泰勒和巴切勒的流體力學(xué)討論班,前者建立了當(dāng)代波動(dòng)預(yù)測理論的數(shù)學(xué)基礎(chǔ),是波-結(jié)構(gòu)作用研究領(lǐng)域的先驅(qū),后者則是空氣動(dòng)力學(xué)中擾動(dòng)分析法的創(chuàng)建者以及Annual Review of Fluid Mechanics的創(chuàng)刊人.此外,建立橢球粒子在黏性流體中的運(yùn)動(dòng)方程的George Jeffery(1891—1957)、氣動(dòng)聲學(xué)奠基人James Lighthill(1924—1998)、磁流體動(dòng)力學(xué)及應(yīng)用領(lǐng)域的Arthur Shercliff (1927—1983)、波浪理論和氣動(dòng)聲學(xué)領(lǐng)域的David Crighton(1942—2000)也均是這一時(shí)期劍橋大學(xué)流體力學(xué)學(xué)派濃郁學(xué)術(shù)交流氛圍的參與者和受益者.他們的學(xué)生中也不乏享譽(yù)世界的流體力學(xué)大家,例如A.Shercliff的學(xué)生Julian Hunt 便是當(dāng)代環(huán)境流體力學(xué)領(lǐng)域的翹楚,培養(yǎng)了包括目前湍流多相流領(lǐng)域的著名學(xué)者S.Balachandar 在內(nèi)的一大批流體力學(xué)家;J.Lighthill則培養(yǎng)了超音速推進(jìn)器、動(dòng)力波、非線性擴(kuò)散波理論和連續(xù)介質(zhì)振動(dòng)理論方面的著名學(xué)者Gerald B.Whitham (1927—2014),后者是目前湍流邊界層和壁湍流領(lǐng)域著名學(xué)者Javier Jimenez 的導(dǎo)師.此外,環(huán)境和工業(yè)流動(dòng)領(lǐng)域的著名學(xué)者Paul Linden、高雷諾數(shù)壁湍流領(lǐng)域的著名學(xué)者Ivan Marusic、湍流動(dòng)力系統(tǒng)理論方面著名學(xué)者Rich Kerswell 也都可追根溯源到劍橋大學(xué)的師承關(guān)系.

其次是現(xiàn)代流體力學(xué)的另一處圣地美國.約翰霍普金斯大學(xué)的著名學(xué)者Charles Meneveau 師承于紐約大學(xué)的流體力學(xué)家Katepalli R.Sreenivasa,后者的導(dǎo)師則是上文提到的加州理工學(xué)派的R.Narasimha;圖1 中的Robert Kraichnan (1928—2008)是愛因斯坦的最后一任助手,也是湍流統(tǒng)計(jì)理論近現(xiàn)代方法的建立者,他培養(yǎng)了目前湍流動(dòng)力系統(tǒng)理論領(lǐng)域的著名學(xué)者U.Frisch.計(jì)算流體力學(xué)領(lǐng)域,大渦模擬(LES)方法的先驅(qū)William Craig Reynolds (1933—2004)是斯坦福湍流研究中心的創(chuàng)始人,他培養(yǎng)了渦動(dòng)力學(xué)、湍流小尺度結(jié)構(gòu)動(dòng)力學(xué)領(lǐng)域的著名學(xué)者Fazle Hussain 和DNS 方法的奠基人Parviz Moin,后者是目前DNS 應(yīng)用數(shù)值計(jì)算領(lǐng)域著名學(xué)者Robert Moser的導(dǎo)師.

近現(xiàn)代流體力學(xué)發(fā)展史中還有一支不得不提的分支——中國學(xué)派.圖1 中只列出了兩位中國籍的流體力學(xué)家: 周培源和鄭曉靜,事實(shí)上陸士嘉、錢學(xué)森、郭永懷、羅時(shí)鈞、莊逢甘等均是“哥廷根學(xué)派”和“加州理工學(xué)派”在中國的傳承者.其中陸士嘉先生是普朗特的唯一女弟子,是我國第一個(gè)空氣動(dòng)力學(xué)專業(yè)的創(chuàng)始人;錢學(xué)森(1911—2009)先生同馮·卡門一起建立了高亞聲速流氣動(dòng)力的卡門一錢公式,提出跨聲速流動(dòng)相似律、上下臨界馬赫數(shù)等概念,開創(chuàng)了高超聲速流和稀薄氣體動(dòng)力學(xué)新領(lǐng)域[31];郭永懷先生在跨聲速流的穩(wěn)定性、激波邊界層相互作用及高超聲速流等領(lǐng)域均作出了突出的貢獻(xiàn),為解決邊界層的奇異性,他改進(jìn)了龐加萊、萊特希爾的變形參數(shù)和變形坐標(biāo)法,發(fā)展了奇異攝動(dòng)理論,后被錢學(xué)森命名為PLK 方法[32];羅時(shí)鈞先生是我國最早使用有限差分法計(jì)算飛機(jī)空氣動(dòng)力的學(xué)者,主持完成了我國跨音速?機(jī)身?平尾?垂尾組合體縱向空氣動(dòng)力差分計(jì)算程序,首次解決大迎角非線性氣動(dòng)力計(jì)算收斂問題,系國際上首次得到非對稱氣動(dòng)力計(jì)算結(jié)果,并取得計(jì)算方法上的突破,具有很高的理論和應(yīng)用價(jià)值[33];莊逢甘先生在旋渦、激波和非平衡起主導(dǎo)作用的復(fù)雜流動(dòng)方面取得了當(dāng)時(shí)國際領(lǐng)先水平的成果,長期從事導(dǎo)彈、火箭、再入飛行器的空氣動(dòng)力學(xué)研究,在大型風(fēng)洞設(shè)計(jì)與建造、運(yùn)載工具的氣動(dòng)研究試驗(yàn)、非定常旋渦主導(dǎo)的空氣動(dòng)力學(xué)、計(jì)算流體學(xué)研究等方面均做出了重要貢獻(xiàn),在湍流統(tǒng)計(jì)理論方面,在Heisenberg 譜傳輸項(xiàng)的假設(shè)下,首次得到了準(zhǔn)確的湍流譜解,給出了Burger 方程的初值問題的準(zhǔn)確解,對有隨機(jī)邊界條件的N-S 方程進(jìn)行了長期的研究,提出了雙尺度湍流概念[34].此外,我國在科技發(fā)展和應(yīng)用需求的大背景下涌現(xiàn)處了一批杰出的流體力學(xué)學(xué)者,并對現(xiàn)代流體力學(xué)發(fā)展做出了重要貢獻(xiàn).文獻(xiàn)[19,35]對流體力學(xué)在中國的發(fā)展及中國學(xué)者的貢獻(xiàn)進(jìn)行了系統(tǒng)的論述,受篇幅所限,本文不再詳述.

4 流體力學(xué)理論發(fā)展與應(yīng)用需求的結(jié)合

現(xiàn)代流體力學(xué)的活力源于不同學(xué)科中流體力學(xué)應(yīng)用需求的強(qiáng)力驅(qū)動(dòng).隨著研究對象一步一步的拓展細(xì)化,從20 世紀(jì)中后期開始流體力學(xué)發(fā)生了與多個(gè)學(xué)科的交叉融合,流體力學(xué)自身也從對普適流動(dòng)機(jī)理、模型的孜孜追求拓展變得更加務(wù)實(shí).針對環(huán)境流動(dòng)問題,通過應(yīng)用流體力學(xué)的基本原理解釋自然界,特別是大氣和海洋中流動(dòng)現(xiàn)象的動(dòng)力學(xué)性質(zhì),逐漸形成了環(huán)境流體力學(xué),派生出海岸/海洋工程流體力學(xué)、大氣環(huán)境流體力學(xué)、水環(huán)境流體力學(xué)和地球流體力學(xué)等分支學(xué)科,主要研究地球表層(土壤上層,海洋表層與大氣近地層)的流動(dòng)與輸運(yùn);針對生物醫(yī)學(xué)等領(lǐng)域的流動(dòng)現(xiàn)象機(jī)理,發(fā)展演變出了生物流體力學(xué),主要研究動(dòng)物和人體內(nèi)循環(huán)、呼吸系統(tǒng)的生理流體(如血液、氣體、尿液、淋巴液和其他體液等)的流體力學(xué)問題;針對核物理、天體物理中的等離子體流動(dòng),發(fā)展了磁流體力學(xué),主要研究導(dǎo)電流體與磁場相互作用的動(dòng)力學(xué)或運(yùn)動(dòng)規(guī)律,包括磁流體力學(xué)波與穩(wěn)定性問題等;針對工業(yè)中的界面和摩擦問題,發(fā)展了浸潤與界面力學(xué);針對物理化學(xué)過程中與燃燒、擴(kuò)散、滲析、電泳、聚并、流態(tài)化、毛細(xì)流等現(xiàn)象,發(fā)展了物理化學(xué)流體力學(xué)等等.根據(jù)我國力學(xué)學(xué)會(huì)流體力學(xué)專委會(huì)下設(shè)的專業(yè)組的劃分,也可以看出學(xué)科分支發(fā)展的不斷衍生.目前下設(shè)的專業(yè)組有相對傳統(tǒng)的分支,如湍流與穩(wěn)定性,非牛頓流體力學(xué)等,也有包含了顯著應(yīng)用背景和學(xué)科交叉特征的分支,如工業(yè)流體力學(xué)、高溫氣體動(dòng)力學(xué)等.

新興的分支為流體力學(xué)發(fā)展注入了新的發(fā)展動(dòng)能,成為了流體力學(xué)研究活躍的前沿領(lǐng)域,新興分支的重要代表性研究成果也引起了學(xué)術(shù)界的積極評價(jià)和鼓勵(lì).以Batchelor 獎(jiǎng)為例,自2007 年該獎(jiǎng)項(xiàng)設(shè)立以來每四年評選一次,至今共評出了4 位獲獎(jiǎng)?wù)?分別是: Howard Stone (2008),Detlef Lohse (2012),Raymond E.Goldstein (2016)和Alexander J.Smits(2020).這些獲獎(jiǎng)?wù)邚氖碌难芯考捌浍@獎(jiǎng)的代表性工作均來自新興的學(xué)科分支,其中H.Stone 從事的是生物流體動(dòng)力學(xué)、膠體動(dòng)力學(xué)方面的研究,包括建立了新的廣義泡沫排水方程,提出和檢驗(yàn)了表面張力和表面活性劑效應(yīng);D.Lohse 從事的是多相流、氣泡聲致發(fā)光、湍流對流和微流體動(dòng)力學(xué)方面的研究;R.E.Goldstein 從事的是自然界中的非平衡現(xiàn)象,特別是生物物理學(xué)方面的研究,貢獻(xiàn)包括對活性物質(zhì)的實(shí)驗(yàn)研究、多細(xì)胞物理學(xué)等;A.J.Smits 從事的是高雷諾數(shù)和高馬赫數(shù)下壁面湍流結(jié)構(gòu)的實(shí)驗(yàn)研究,以及仿生推進(jìn)和減阻方面的工作.隨著流體力學(xué)與其他學(xué)科交叉融合的深入,來自應(yīng)用流體力學(xué)分支的學(xué)者獲得Batchelor 獎(jiǎng)將成為趨勢.

流體力學(xué)的新興學(xué)科分支的產(chǎn)生并非突然,而是伴隨著流體力學(xué)基本理論、計(jì)算模擬和實(shí)驗(yàn)研究方法的不斷發(fā)展更替以及實(shí)際應(yīng)用需求的不斷萌生而逐漸衍生出來的.諸多流體力學(xué)分支學(xué)科的發(fā)展都驗(yàn)證了此規(guī)律,如文獻(xiàn)[36]介紹的等離子體流體力學(xué)、文獻(xiàn)[37]介紹的爆炸氣動(dòng)力學(xué)、文獻(xiàn)[38]介紹的小型器件中的工程流體力學(xué)、文獻(xiàn)[39]介紹的化學(xué)流體動(dòng)力學(xué)等等.此處僅以環(huán)境流體力學(xué)的研究為例,圖1 列舉的流體力學(xué)家中,環(huán)境力學(xué)領(lǐng)域的學(xué)者占了20 席,其中5 位處于20 世紀(jì)中葉前,有15 位處于現(xiàn)代流體力學(xué)階段.最早的環(huán)境力學(xué)研究可追溯到1904 年挪威物理學(xué)家Vilhelm Bjerknes(1862—1951)開始的從動(dòng)力學(xué)和熱力學(xué)角度研究大尺度大氣和海洋運(yùn)動(dòng),以及他在Meteorologische Zeitschrift雜志上發(fā)表的文章“Das problem der wettervorhersage,betrachtet von standpunkt der mechanik und physik (從力學(xué)和物理學(xué)的角度研究天氣預(yù)報(bào)問題)”[40].20 世紀(jì)初近代流體力學(xué)的4大學(xué)派創(chuàng)始人也都不約而同的將理論研究的成果應(yīng)用到環(huán)境流動(dòng)規(guī)律的揭示和理解中.1915 年,泰勒在Phil.Trans.R.Soc.Lond.A上發(fā)表的“Eddy motion in the atmosphere”[41]可視為大氣湍流研究的最早文獻(xiàn);1932 年,普朗特在德文期刊上發(fā)表過題為“Meteorologische anwendung der str?mungslehre (流動(dòng)理論的氣象應(yīng)用)”[42]的論文,將邊界層理論應(yīng)用于氣象學(xué)的研究;1940 年代,柯爾莫哥洛夫最得意的兩位學(xué)生A.Obukhov 和A.S.Monin 將K41 理論成功應(yīng)用于大氣和海洋湍流的研究,建立了至今仍是大氣邊界層研究的理論基礎(chǔ)O-M 相似理論;即使是身為航空航天大師的馮·卡門,在1947 年也發(fā)表過題為“Sand ripples in the desert”[43]的論文,試圖通過風(fēng)剪切的渦旋結(jié)構(gòu)對風(fēng)成沙波紋的形成進(jìn)行建模.

時(shí)至今日,環(huán)境流體力學(xué)的研究內(nèi)容已經(jīng)發(fā)展得十分豐富,根據(jù)李家春先生在《力學(xué)進(jìn)展》上的綜述[44],大致可以分為: 大氣海洋環(huán)流,大氣海洋中的旋渦運(yùn)動(dòng),大氣海洋中的湍流運(yùn)動(dòng),污染物、溶質(zhì)的輸運(yùn)與湍流擴(kuò)散,沉積物異重流,風(fēng)沙、泥沙運(yùn)動(dòng),海氣相互作用,陸氣相互作用8 個(gè)方面,雖然各個(gè)方向針對的問題不同,但其共性特征是流動(dòng)過程中的多相多組分、多場多過程耦合、多尺度和跨尺度、高度非線性和多自由度等.

以環(huán)境流體力學(xué)中的重要分支風(fēng)沙環(huán)境力學(xué)為例,簡要回顧其研究歷程可以清楚地看出在應(yīng)用需求明顯的分支發(fā)展過程中,流體力學(xué)基本理論、方法的發(fā)展在其中起到的重要作用.從流體力學(xué)的角度,風(fēng)沙運(yùn)動(dòng)被定義為高雷諾數(shù)氣-固兩相稀疏流動(dòng).R.A.Bagnold (1941)在最初建立經(jīng)典風(fēng)沙物理學(xué)體系時(shí)就用到了流體力學(xué)的剪切應(yīng)力、摩阻速度、粗糙度等概念,并利用邊界層理論對風(fēng)沙邊界層的流場進(jìn)行簡化[45],當(dāng)時(shí)邊界層理論由普朗特建立不久,并由馮·卡門等逐漸發(fā)展完善.1964 年,P.R.Owen在Journal of Fluid Mechanics上發(fā)表了“Saltation of uniform grains in air”[46],首次對風(fēng)沙運(yùn)動(dòng)進(jìn)行了流體力學(xué)角度的建模,其中的風(fēng)場模型仍是采用邊界層理論中的平均流廓線基本解.隨著計(jì)算機(jī)技術(shù)的發(fā)展,雷諾平均方程封閉模式的數(shù)值求解成為可能,風(fēng)沙流的研究很快也跟上數(shù)值模擬的步伐.Anderson等[47]利用RANS 對一維風(fēng)沙流開展了模擬研究,獲得與實(shí)驗(yàn)上量級可比的輸沙通量模擬結(jié)果.此后,數(shù)值模擬研究成為了風(fēng)沙流問題研究的重要手段,計(jì)算流體技術(shù)上的每一次進(jìn)步都推動(dòng)著風(fēng)沙環(huán)境力學(xué)的躍變.例如1960 年代,J.Smagorinsky發(fā)展了流動(dòng)的大渦模擬(LES)技術(shù)[48],這種方法可以解析大尺度渦,彌補(bǔ)了RANS 模擬對全尺度湍流進(jìn)行平均導(dǎo)致的完全忽略湍流脈動(dòng)的不足.I.Vinkovic 等[49]首先基于Smagorinsky-Germano 亞格子模型(SGS)的大渦模擬研究顆粒在湍流邊界層的擴(kuò)散問題,獲得了與風(fēng)洞實(shí)驗(yàn)在躍移高度、沖擊速度等方面定量上較RANS 模擬吻合更好的結(jié)果;上世紀(jì)70 年代初,J.W.Deardorff[50]發(fā)展了大雷諾數(shù)流動(dòng)的壁解析大渦模擬(WRLES)技術(shù),考慮到床面顆粒運(yùn)動(dòng)的隨機(jī)性及其對壁面湍流結(jié)構(gòu)的影響,Zheng 等[51]將WRLES方法運(yùn)用到可侵蝕床面風(fēng)沙流的模擬,并第一次將該方法兩相壁湍流模擬的摩擦雷諾數(shù)(Reτ)擴(kuò)展到4200 以上,獲得了與自然界真實(shí)風(fēng)沙流情況一致的比較結(jié)果,同時(shí)刻畫了實(shí)驗(yàn)上難以獲得的沙粒對壁面湍流結(jié)構(gòu)調(diào)制影響的規(guī)律.

流體力學(xué)應(yīng)用學(xué)科中產(chǎn)生的需求也反過來促進(jìn)著流體力學(xué)的內(nèi)生發(fā)展.仍以風(fēng)沙環(huán)境力學(xué)為例,沙塵暴的形成和發(fā)展是一項(xiàng)重要的研究內(nèi)容.作為大氣邊界層內(nèi)發(fā)生的一類極端流動(dòng)過程,Reτ高達(dá)1.0×(106～ 107),湍流結(jié)構(gòu)的最大尺度與其攜帶的顆粒特征尺度相差9 個(gè)量級,且存在多結(jié)構(gòu)層次、多物理場、多過程、多演化速率的強(qiáng)非線性耦合.1990 年代末,高雷諾數(shù)壁湍流中超大尺度結(jié)構(gòu)在管道流動(dòng)中被發(fā)現(xiàn),隨后被大氣表面層的實(shí)驗(yàn)觀測證實(shí)[52].這一壁湍流外區(qū)的典型湍流結(jié)構(gòu)已經(jīng)被證實(shí)對質(zhì)量、動(dòng)量、能量的輸運(yùn)具有重要的影響.鄭曉靜教授領(lǐng)導(dǎo)蘭州大學(xué)風(fēng)沙研究團(tuán)隊(duì)在巴丹吉林沙漠邊緣的青土湖地區(qū)設(shè)計(jì)建設(shè)了廣受關(guān)注和好評并被認(rèn)為全球范圍內(nèi)“獨(dú)一無二”的青土湖觀測列陣,用于對大氣表面層凈風(fēng)和沙塵暴流動(dòng)進(jìn)行觀測研究,并圍繞高雷諾數(shù)壁湍流和兩相流問題取得了一系列成果,她在其有關(guān)高雷諾數(shù)壁湍流研究的綜述論文中系統(tǒng)回顧了該領(lǐng)域的研究脈絡(luò)和重要研究進(jìn)展[53],同時(shí)也指出目前的高雷諾數(shù)壁湍流研究仍面臨著許多困難和挑戰(zhàn),尤其是對沙塵暴這一類極端流動(dòng)的深入研究需要流體力學(xué)發(fā)展新的理論、新的計(jì)算模型甚至模式,并需要針對這一類流動(dòng)全面系統(tǒng)的實(shí)驗(yàn)觀測以及新的數(shù)據(jù)分析手段作為基礎(chǔ),這種需求無疑將對湍流及其穩(wěn)定性、多相流體力學(xué)、計(jì)算流體力學(xué)、實(shí)驗(yàn)流體力學(xué)等的內(nèi)生發(fā)展提供驅(qū)動(dòng)力.

5 總結(jié)與展望

以Batchelor 誕辰100 周年紀(jì)念大會(huì)封面為據(jù),本文簡要回顧了流體力學(xué)近300 年的發(fā)展歷程,發(fā)現(xiàn)流體力學(xué)歷經(jīng)了3 個(gè)重要階段: 第1 個(gè)階段是與應(yīng)用數(shù)學(xué)、物理學(xué)伴生的階段,得益于嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)基礎(chǔ),流體力學(xué)很早便建立了完美的方程,成為數(shù)學(xué)“皇冠”上最閃耀的寶石,但此階段建立的理論在描述廣泛的真實(shí)流動(dòng)現(xiàn)象時(shí)還存在挑戰(zhàn);第2 階段是由工程和自然環(huán)境背景的應(yīng)用需求驅(qū)動(dòng)的發(fā)展階段,這一階段流體力學(xué)的核心進(jìn)步集中在湍流和空氣動(dòng)力學(xué)領(lǐng)域,逐漸形成了通過對實(shí)際問題的觀察、分析,提煉力學(xué)模型,并利用數(shù)學(xué)方法計(jì)算和求解模型,最終獲得規(guī)律或方案的研究范式,這一時(shí)期誕生了4 位對流體力學(xué)發(fā)展產(chǎn)生深遠(yuǎn)影響的“大師”以及諸多“豐碑式”的成就,形成了特色鮮明的學(xué)派;第3 階段是4 大學(xué)派的傳承和多樣性拓展的階段,流體力學(xué)的發(fā)展呈現(xiàn)百花齊放的勢態(tài),與多個(gè)學(xué)科的交叉融合一方面拓寬了流體力學(xué)的外延,另一方面也為流體力學(xué)的內(nèi)生發(fā)展注入了新鮮活力和驅(qū)動(dòng)力.

此外,通過對近300 年來流體力學(xué)重要進(jìn)展的回顧,可以發(fā)現(xiàn)未來流體力學(xué)的進(jìn)一步突破會(huì)更依賴于理論方法和技術(shù)的持續(xù)進(jìn)步和創(chuàng)新,包括但不限于以下領(lǐng)域: 理論方面,非線性方程普適理論與數(shù)值方法、統(tǒng)計(jì)理論的現(xiàn)代方法、群論在流體力學(xué)研究中的更廣泛運(yùn)用、湍流的動(dòng)力系統(tǒng)理論、湍流結(jié)構(gòu)的數(shù)學(xué)理論等;數(shù)值計(jì)算方面,RANS,LES,DNS,Lattic-Boltzmann 法、小波等數(shù)值算法在更廣泛流動(dòng)應(yīng)用范圍上的拓展以及計(jì)算效率、分辨率、緊致性、網(wǎng)格自適應(yīng)性等方面的大幅提升等;實(shí)驗(yàn)方面,面向極端(極高雷諾數(shù)、馬赫數(shù)或微納米尺度)流動(dòng)的實(shí)驗(yàn)裝置與測量顯示技術(shù)、面向非平穩(wěn)數(shù)據(jù)的處理分析方法、面向大數(shù)據(jù)的同化與人工智能方法等.