垂向雙蝠鲼變攻角滑翔水動(dòng)力性能研究1)

高鵬騁 劉冠杉 黃橋高 ,2) 潘 光 馬云龍

* (西北工業(yè)大學(xué)航海學(xué)院,西安 710072)

? (中國船舶集團(tuán)有限公司系統(tǒng)工程研究院,北京 100094)

引言

魚類集群運(yùn)動(dòng)的現(xiàn)象隨處可見,集群游動(dòng)能幫助魚群中各個(gè)體有效規(guī)避捕食者,提升捕食效率,增加繁殖機(jī)會(huì)等[1-3].此外,許多學(xué)者認(rèn)為魚類可以通過高度組織化的群體運(yùn)動(dòng)來保存能量,獲得水動(dòng)力優(yōu)勢,提高個(gè)體的運(yùn)動(dòng)性能.

大多數(shù)研究認(rèn)為,魚群游動(dòng)的水動(dòng)力優(yōu)勢是由于渦流假說和槽道效應(yīng)[4].其中,渦流假說認(rèn)為,魚群中后魚置身于前魚的尾渦中,通過傳入的尾渦結(jié)構(gòu)的誘導(dǎo)速度降低了魚和水流間的相對速度,后魚同時(shí)還能借助前魚尾渦提高游動(dòng)效率.槽道效應(yīng)指出,通過增加相鄰魚之間在游泳方向的水流速度來降低魚和水流間的相對速度,同時(shí)魚類還可以借助相鄰魚渦街誘導(dǎo)出的流動(dòng)來提高游動(dòng)效率.

近年來,隨著計(jì)算方法以及數(shù)值仿真軟件的發(fā)展,學(xué)者們對魚群水動(dòng)力性能進(jìn)行了大量仿真計(jì)算,并得到了許多有意義的結(jié)論.Deng 等[5]采用改進(jìn)的浸入邊界法對菱形魚群中的3 條魚單元進(jìn)行了數(shù)值模擬.結(jié)果表明,位于前一列兩條魚之間的后魚可以利用上游魚脫落的反卡門渦街來提高推進(jìn)效率以及降低功耗.隨后,Chung[6]在文獻(xiàn)[5]的基礎(chǔ)上進(jìn)行了深入研究,給定了3 條魚最優(yōu)的位置及運(yùn)動(dòng)參數(shù)設(shè)置,即兩條前魚橫向間距為0.4 倍弦長,進(jìn)行反相波動(dòng)運(yùn)動(dòng),后魚的前緣距前魚后緣0.2 倍弦長.Tian 等[7]通過有限元法數(shù)值求解不可壓縮的Navier-Stokes 方程來研究子母魚對的游泳性能和渦結(jié)構(gòu),計(jì)算結(jié)果表明母魚和小魚在串聯(lián)和交錯(cuò)排列中都受益,通過改變它們的相位差和相速度,可增加推力和降低功耗.目前,還有不少學(xué)者利用強(qiáng)化學(xué)習(xí)算法來對先導(dǎo)-跟隨群游結(jié)構(gòu)中的跟隨魚進(jìn)行運(yùn)動(dòng)控制,其中先導(dǎo)魚的運(yùn)動(dòng)方式固定,跟隨魚通過強(qiáng)化學(xué)習(xí)來調(diào)整運(yùn)動(dòng)方式,以實(shí)現(xiàn)跟隨魚利用先導(dǎo)魚的渦流來提升推進(jìn)效率[8-9].

王亮[10]對二維仿真魚群游動(dòng)進(jìn)行了數(shù)值模擬,指出當(dāng)魚群中各個(gè)體存在體形差異時(shí)主要利用側(cè)向水動(dòng)力(即槽道效應(yīng))來提高推進(jìn)效率;當(dāng)個(gè)體體形相近時(shí),主要利用前魚尾渦提高效率.Li 等[11]對串聯(lián)、并聯(lián)、菱形和矩形4 種編隊(duì)的魚群游動(dòng)進(jìn)行了數(shù)值模擬.結(jié)果表明,效率受到尾流和側(cè)向壓力的影響,其中尾流主要影響推力,橫向功率損失受到側(cè)向壓力影響.Lin 等[12-15]對二維鰻式游動(dòng)魚群開展了系列研究,探究了相位差、間距對串聯(lián)魚群及傾斜布置魚群的水動(dòng)力性能影響.

隨著電機(jī)驅(qū)動(dòng)技術(shù),傳感器技術(shù)以及流場顯示技術(shù)的發(fā)展,一些學(xué)者開始設(shè)計(jì)搭建實(shí)驗(yàn)裝置來研究魚群游動(dòng)的節(jié)能機(jī)理[16-21].Dewey 等[16-17]與Boschitsch 等[18]分別實(shí)驗(yàn)研究了兩個(gè)柔性撲翼在并聯(lián)與串聯(lián)布置時(shí)的水動(dòng)力性能,并利用DPIV 系統(tǒng)進(jìn)行流場記錄及顯示.實(shí)驗(yàn)結(jié)果表明,對于并聯(lián)結(jié)構(gòu),兩個(gè)翼形的推進(jìn)特性相同: 同相拍動(dòng)時(shí),效率提升而推力減小(相對于單個(gè)翼形);反相拍動(dòng)時(shí),推力增加而效率基本不變.對于串聯(lián)結(jié)構(gòu),前翼的推力和效率在分離距離較大時(shí)與單個(gè)翼形一致,而后翼由于受到前翼尾流的影響,其動(dòng)力學(xué)特性與分離距離和相位差相關(guān).

當(dāng)前國內(nèi)外關(guān)于集群水動(dòng)力特性研究廣泛集中于二維翼型而非三維生物的研究.并且,研究主要集中在二維平面的群游,而沒有考慮到集群中各單體沿垂向分布的情況,然而通過Vicsek 等[22]的研究表明生物在實(shí)際游動(dòng)過程中往往采取上下錯(cuò)落分布隊(duì)形.此外,目前的研究對象大多為尾鰭擺動(dòng)推進(jìn)魚群,忽略了對采用滑撲結(jié)合推進(jìn)的鰩科生物的研究.

蝠鲼屬鰩科生物,有著扁平形的身體、較大的展弦比,巡游速度在0.25～0.47 m/s[23].蝠鲼采用撲動(dòng)與滑翔相結(jié)合的推進(jìn)方式[24],效率可高達(dá)89%,高于鰻科、鲹科等水中生物[25-27],在機(jī)動(dòng)性、隱蔽性等方面具有超凡的優(yōu)越性.為彌補(bǔ)現(xiàn)有研究的不足以及探究雙蝠鲼垂向間距和攻角(α)對各個(gè)蝠鲼水動(dòng)力性能的影響,本文針對沿垂向分布的雙蝠鲼進(jìn)行滑翔運(yùn)動(dòng)時(shí)的水動(dòng)力特性開展研究,其中垂向間距選取了0.25TL(TL為體厚),0.5TL,0.75TL,1TL4 種工況,在每種工況下進(jìn)行了攻角變換,變化范圍為?8°～8°(每2°取一個(gè)特征攻角),以期為仿蝠鲼滑撲一體航行器在滑翔時(shí)的隊(duì)形設(shè)置提供參考數(shù)據(jù).

1 數(shù)值計(jì)算方法

1.1 仿真模型及計(jì)算域設(shè)置

采用逆向工程技術(shù)建立蝠鲼數(shù)值計(jì)算模型,通過測量實(shí)際物體的尺寸,獲得物體的三維點(diǎn)數(shù)據(jù),再通過點(diǎn)數(shù)據(jù)構(gòu)建三維曲線,進(jìn)一步構(gòu)建三維曲面,進(jìn)而重構(gòu)實(shí)物的CAD 模型[28],如圖1 所示.其中展長(SL)為2900 mm,體長(BL)為1800 mm,最大體厚為350 mm.

圖1 蝠鲼模型Fig.1 Manta ray model

我們將4 種間距排布統(tǒng)一展示在圖2 中,計(jì)算域尺寸根據(jù)實(shí)際排布方式進(jìn)行適應(yīng)性調(diào)整,其中保證入口與蝠鲼間距4 倍體長,出口與蝠鲼間距7 倍體長,展向壁面距蝠鲼3 倍展長,上、下壁面分別距上下蝠鲼3 倍體厚.邊界條件設(shè)置如下: 入口邊界設(shè)為速度入口,出口邊界設(shè)為壓力出口,壁面設(shè)為自由滑移壁面,蝠鲼表面設(shè)為靜止無滑移壁面.

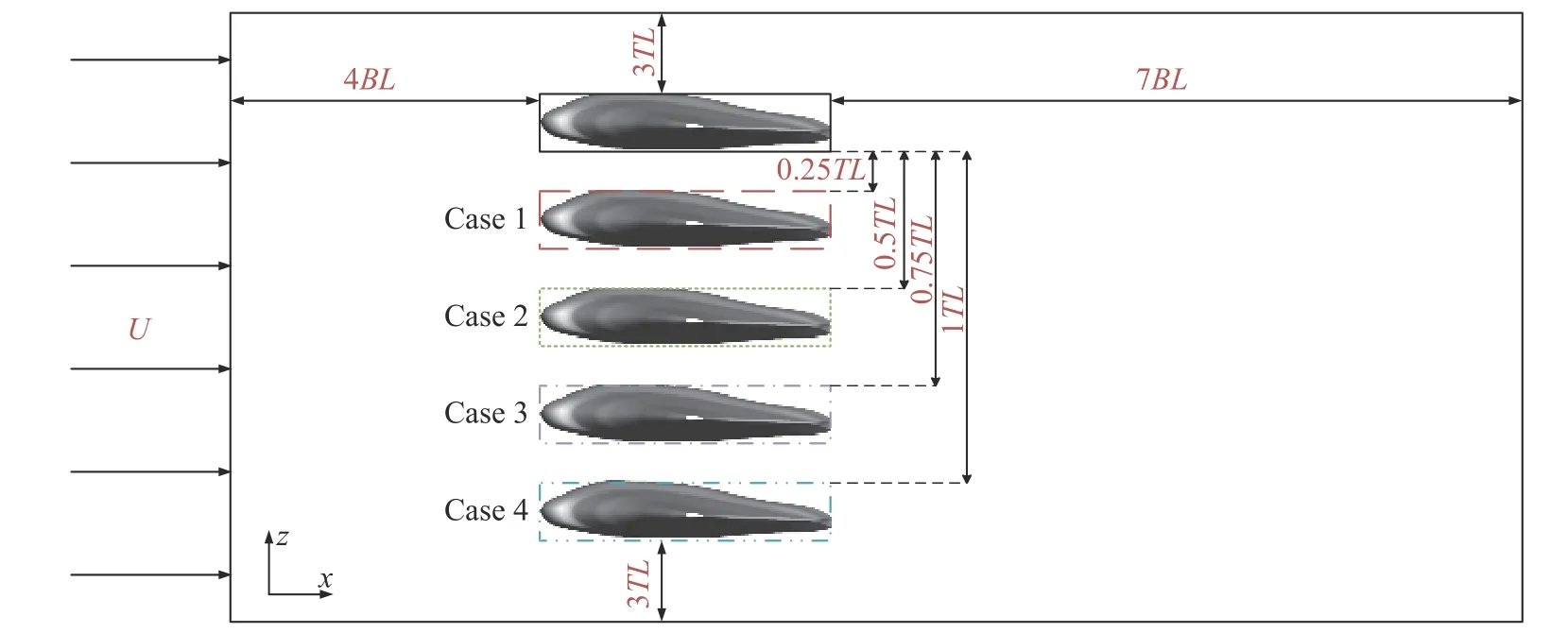
圖2 計(jì)算域設(shè)置Fig.2 Calculation domain setting

本文在4 組垂向間距(0.25TL～1TL)以及9 組攻角(?8°～8°)組合下進(jìn)行了仿真計(jì)算,探究了集群滑翔時(shí),垂向間距和攻角對集群中各單體和集群系統(tǒng)的水動(dòng)力特性的影響.

1.2 水動(dòng)力參數(shù)定義

根據(jù)文獻(xiàn)[29],雙體蝠鲼滑翔狀態(tài)下的系統(tǒng)平均阻力(Ddouble)按照下式計(jì)算

其中,Dup和Ddown分別代表了上、下蝠鲼所受到的阻力.

將蝠鲼集群滑翔過程中的受力無量綱化

其中,D,L為蝠鲼所受的阻力、升力,ρ為流體密度,U為來流速度,BL為蝠鲼體長.

2 網(wǎng)格無關(guān)性驗(yàn)證與數(shù)值驗(yàn)證

2.1 網(wǎng)格無關(guān)性驗(yàn)證

本文借助ICEM 進(jìn)行結(jié)構(gòu)網(wǎng)格繪制,由疏到密繪制了4 套網(wǎng)格(網(wǎng)格數(shù)量分別為1.5 × 106,3 × 106,4.5 × 106,6 × 106)進(jìn)行單體仿真計(jì)算,以期確定出在保證計(jì)算精度前提下兼顧計(jì)算速度的網(wǎng)格節(jié)點(diǎn)設(shè)置(如圖3(a)所示).圖3(b)展示了在4 套網(wǎng)格下,蝠鲼單體在0°攻角下以0.5 m/s 速度滑翔的阻力系數(shù)(CD)、升力系數(shù)(CL)數(shù)值仿真結(jié)果.可以看出當(dāng)單體網(wǎng)格設(shè)置為4.5 × 106時(shí),計(jì)算結(jié)果精確度已經(jīng)達(dá)到最優(yōu),為節(jié)省計(jì)算成本,提高計(jì)算速度,在后續(xù)的雙體蝠鲼仿真計(jì)算中我們沿用了此時(shí)的節(jié)點(diǎn)設(shè)置.

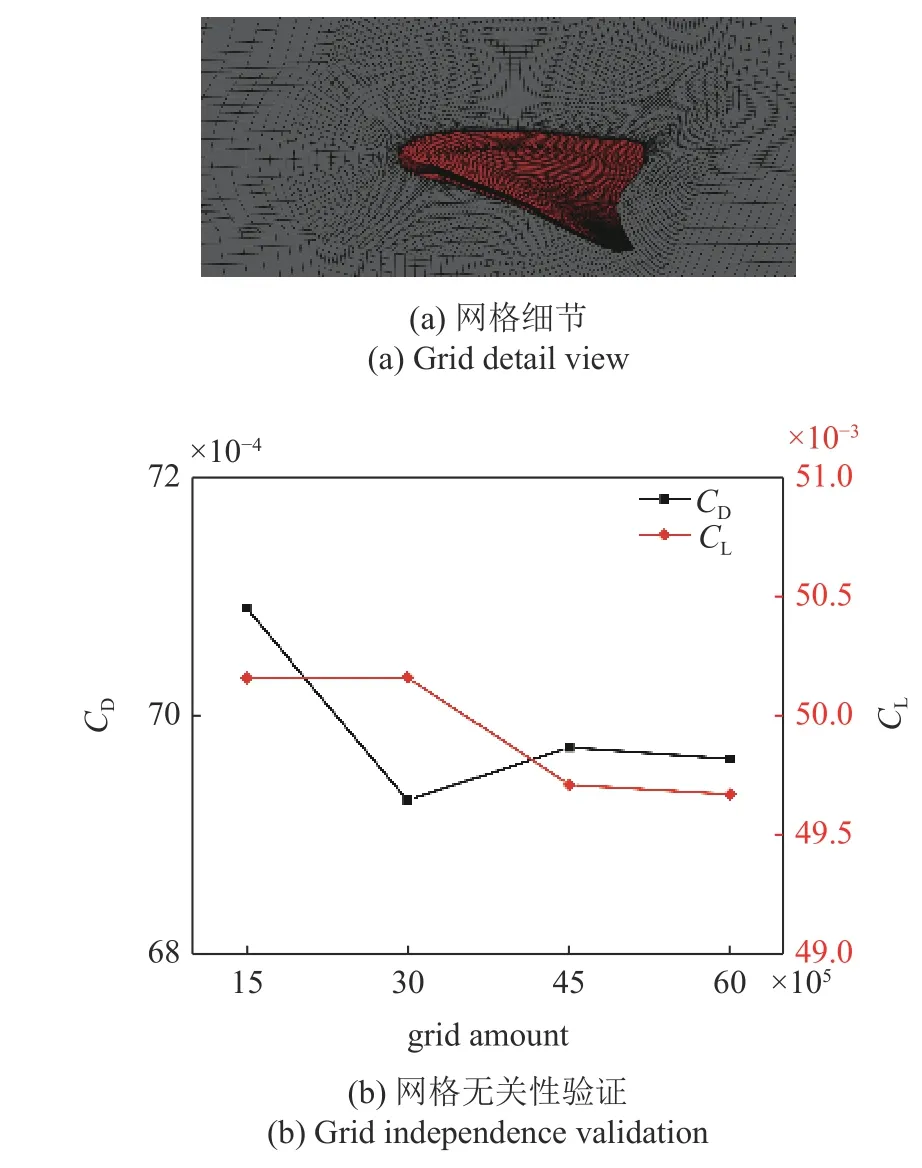
圖3 網(wǎng)格細(xì)節(jié)及無關(guān)性驗(yàn)證Fig.3 Grid detail and independence verification

2.2 數(shù)值計(jì)算方法驗(yàn)證

本文借助 FLUENT 軟件進(jìn)行計(jì)算,湍流模型設(shè)置為SSTk-ω模型,采用 SIMPLEC 算法對連續(xù)方程中的壓力和速度的耦合,收斂殘差設(shè)置為1.0 × 10?5.

采用此方法對三維漸變NACA0009 翼型在雷諾數(shù)Re=1.0 × 106時(shí)不同攻角下的阻力系數(shù)(CD)、升力系數(shù)(CL)進(jìn)行了仿真計(jì)算,并與文獻(xiàn)[30]的實(shí)驗(yàn)數(shù)據(jù)進(jìn)行比對,如圖4 所示.由圖4 可知: 數(shù)值仿真所得到的CD和CL與實(shí)驗(yàn)值接近,確保了數(shù)值計(jì)算方法的可靠性.

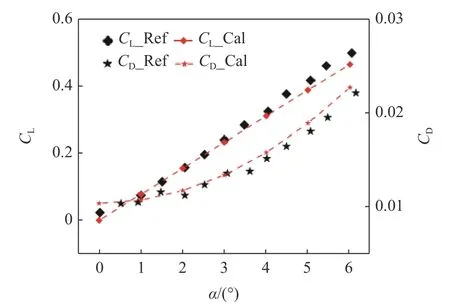
圖4 方法驗(yàn)證Fig.4 Method validation

3 數(shù)值計(jì)算結(jié)果與分析

本節(jié)展示了雙蝠鲼以0.5 m/s 速度滑翔時(shí),不同垂向間距下阻力(升力)系數(shù)隨攻角的變化情況.研究發(fā)現(xiàn),間距和攻角對各阻力系數(shù)產(chǎn)生較大影響,但對升力系數(shù),尤其是系統(tǒng)平均升力系數(shù)影響較小.因此,本節(jié)按照垂向間距劃分小節(jié),在每小節(jié)中結(jié)合壓力云圖對各阻力系數(shù)進(jìn)行分析,在垂向間距為0.25TL時(shí)結(jié)合蝠鲼表面壓力云圖探究升力系數(shù)變化.

3.1 垂向間距0.25TL

本小節(jié)對垂向間距0.25TL的雙蝠鲼集群滑翔進(jìn)行了數(shù)值模擬,集群中各單體攻角保持同步變化,變化范圍為?8°～8°.圖5 展示了上(下)方蝠鲼阻力(升力)系數(shù)、雙蝠鲼系統(tǒng)平均阻力(升力)系數(shù)以及單體蝠鲼阻力(升力)系數(shù)隨攻角變化的改變情況.由圖5(a)可以看出,系統(tǒng)平均阻力均大于單體滑翔時(shí)所受到的阻力.但當(dāng)雙蝠鲼以負(fù)攻角滑翔時(shí),下方蝠鲼受到阻力遠(yuǎn)低于單體滑翔,尤其是在?8°攻角時(shí),幾乎不受到阻力;當(dāng)以正攻角滑翔時(shí),上方蝠鲼受到的阻力減小,下方蝠鲼受到阻力增加.與此同時(shí),我們還發(fā)現(xiàn)當(dāng)攻角為?2°時(shí),上下兩蝠鲼受到的阻力幾乎相同.由圖5(b)可以看出,當(dāng)滑翔攻角小于?2°時(shí),系統(tǒng)平均升力大于單體滑翔時(shí)的升力;當(dāng)滑翔攻角大于?2°時(shí),系統(tǒng)平均升力小于單體滑翔時(shí)的升力;當(dāng)滑翔攻角為?2°時(shí),系統(tǒng)平均升力與單體滑翔升力接近.此外,我們還發(fā)現(xiàn)上方蝠鲼所受升力始終小于下方蝠鲼.

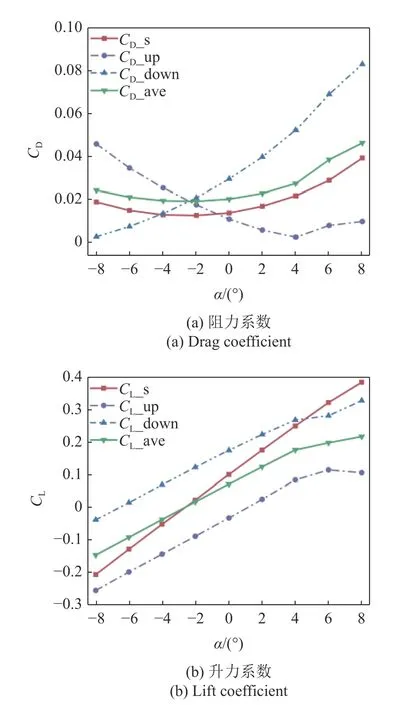
圖5 0.25TL 垂向間距時(shí)不同攻角下的阻力/升力系數(shù)Fig.5 Drag/lift coefficient at different attack angles at 0.25TL vertical distance

為進(jìn)一步探究阻力(升力)出現(xiàn)變化的原因,我們將壓力/速度云圖繪制在了圖6 中,其中壓力取值范圍為?300～150 Pa,速度取值范圍為0～0.8 m/s,后續(xù)所有云圖中取值范圍保持一致.從圖6(a)和圖6(b)可以看出,無論以何種攻角進(jìn)行集群滑翔時(shí),蝠鲼外圍壓力場分布相似,即在蝠鲼的頭部及尾部附近各存在著一個(gè)高壓區(qū),高壓區(qū)的面積及壓力大小幾乎一致.當(dāng)蝠鲼集群以不同攻角集群滑翔時(shí),集群中各單體出現(xiàn)阻力差異的原因在于各單體的表面壓力出現(xiàn)變化.由圖6(a)可以看出,下方蝠鲼頭部的中下部分處于低壓區(qū),而上方蝠鲼頭部完全處于高壓區(qū),這必然導(dǎo)致下方蝠鲼的阻力減小,上方蝠鲼的阻力增加.由圖6(b)可以看出,當(dāng)以正攻角進(jìn)行集群滑翔時(shí),上方蝠鲼頭部的中上部分處于低壓區(qū),下方蝠鲼頭部完全處于高壓區(qū),因此下方蝠鲼的阻力增加,上方蝠鲼的阻力減小.接下來,結(jié)合圖6(c)解釋上下兩蝠鲼升力表現(xiàn),從圖6(c)中可以看出,上下兩蝠鲼上表面壓力分布基本相似,下方蝠鲼頭部壓力略高于上方蝠鲼;下方蝠鲼下表面壓力明顯高于上方蝠鲼,尤其是在蝠鲼的中腹部,上方蝠鲼存在著明顯的低壓區(qū).又因?yàn)樯κ鼙砻鎵毫τ绊戄^大,因此下方蝠鲼所受升力總是大于上方蝠鲼.由圖6(d)可以看出兩蝠鲼中間區(qū)域速度最高,尾部速度最低,頭部存在小面積低速區(qū),因此在蝠鲼尾部及頭部出現(xiàn)高壓區(qū),在兩蝠鲼中腹部周圍出現(xiàn)低壓區(qū),這和壓力云圖相契合.通過結(jié)果統(tǒng)計(jì),我們發(fā)現(xiàn)雙蝠鲼沿垂向分布集群滑翔時(shí)各升力系數(shù)幾乎不受間距和攻角的影響,在后續(xù)小節(jié)中為避免重復(fù),僅結(jié)合壓力云圖對阻力表現(xiàn)進(jìn)行分析.與此同時(shí),我們發(fā)現(xiàn)隨著間距的增加,集群滑翔對速度場影響逐步減弱,我們后續(xù)僅在間距為1TL時(shí)展示速度云圖.

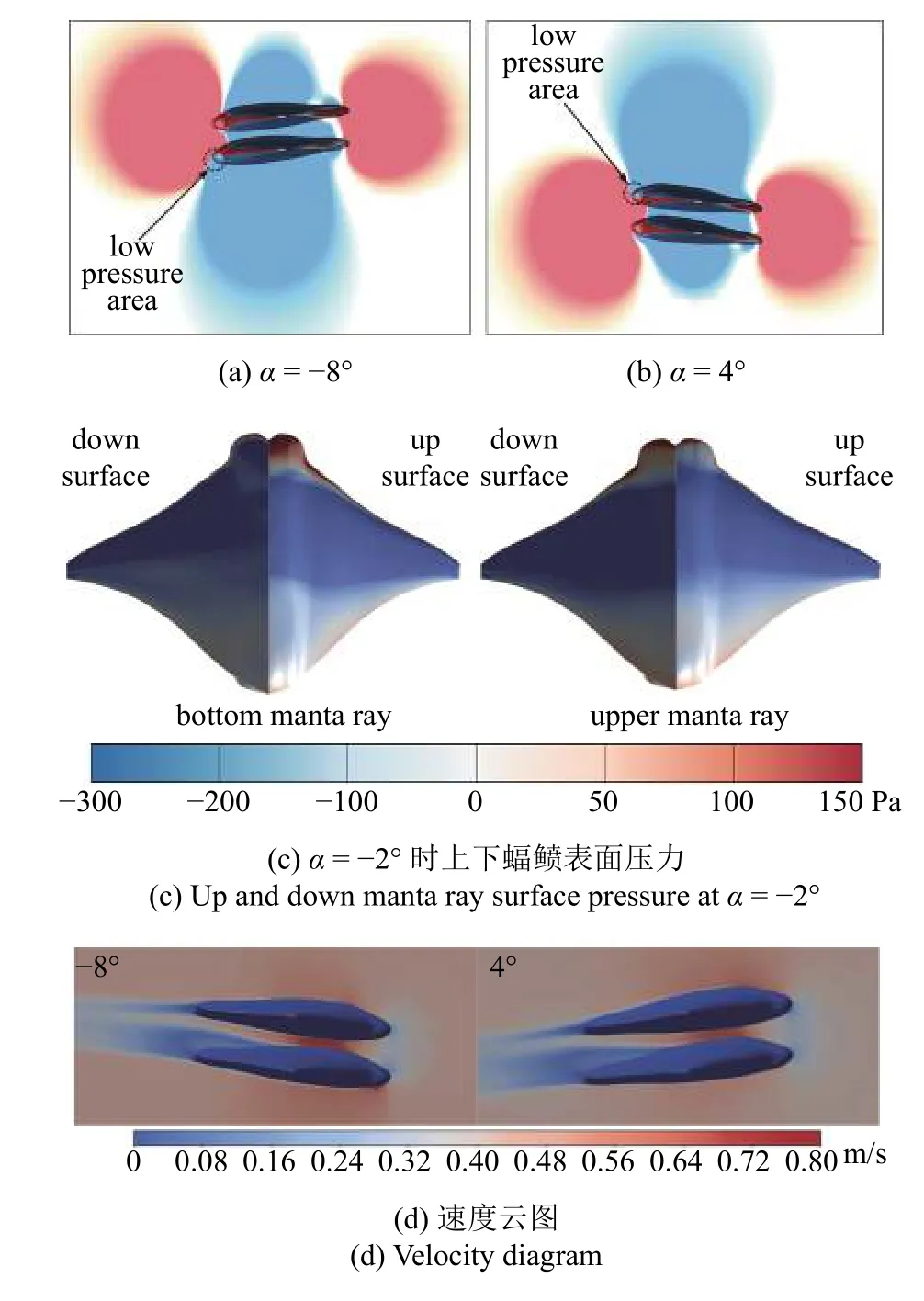
圖6 0.25TL 垂向間距時(shí)不同攻角下的壓力/速度云圖Fig.6 Pressure/velocity diagram at different attack angles at 0.25TL vertical distance

3.2 垂向間距0.5TL

同3.1 節(jié),圖7 展示了當(dāng)垂向間距為0.5TL時(shí),上(下)方蝠鲼阻力(升力)系數(shù)、系統(tǒng)平均阻力(升力)系數(shù)以及單體蝠鲼阻力(升力)系數(shù)隨攻角變化的改變情況.由圖7(a)可以看出,系統(tǒng)平均阻力仍大于單體滑翔時(shí)所受到的阻力,但相較于0.25TL間距時(shí),有所下降.上(下) 方蝠鲼的阻力變化趨勢同0.25TL一致.由圖7(b)可以看出,系統(tǒng)平均升力變化不大,上下兩蝠鲼升力差值減小.

同樣,我們將?8°,4°時(shí)的壓力云圖繪制在了圖8 中,壓力云圖分布情況同間距為0.25TL時(shí)大致相同,從圖8(a)可以看出,在以負(fù)攻角滑翔時(shí),上方蝠鲼頭部的中下部開始出現(xiàn)低壓區(qū),這將導(dǎo)致上方蝠鲼的阻力出現(xiàn)下降,這與圖5 和圖7 的阻力系數(shù)曲線圖相符.當(dāng)以正攻角滑翔時(shí),上下蝠鲼的表面壓力相較于間距為0.25TL時(shí)沒有明顯變化,因此在推力曲線上也幾乎一致.

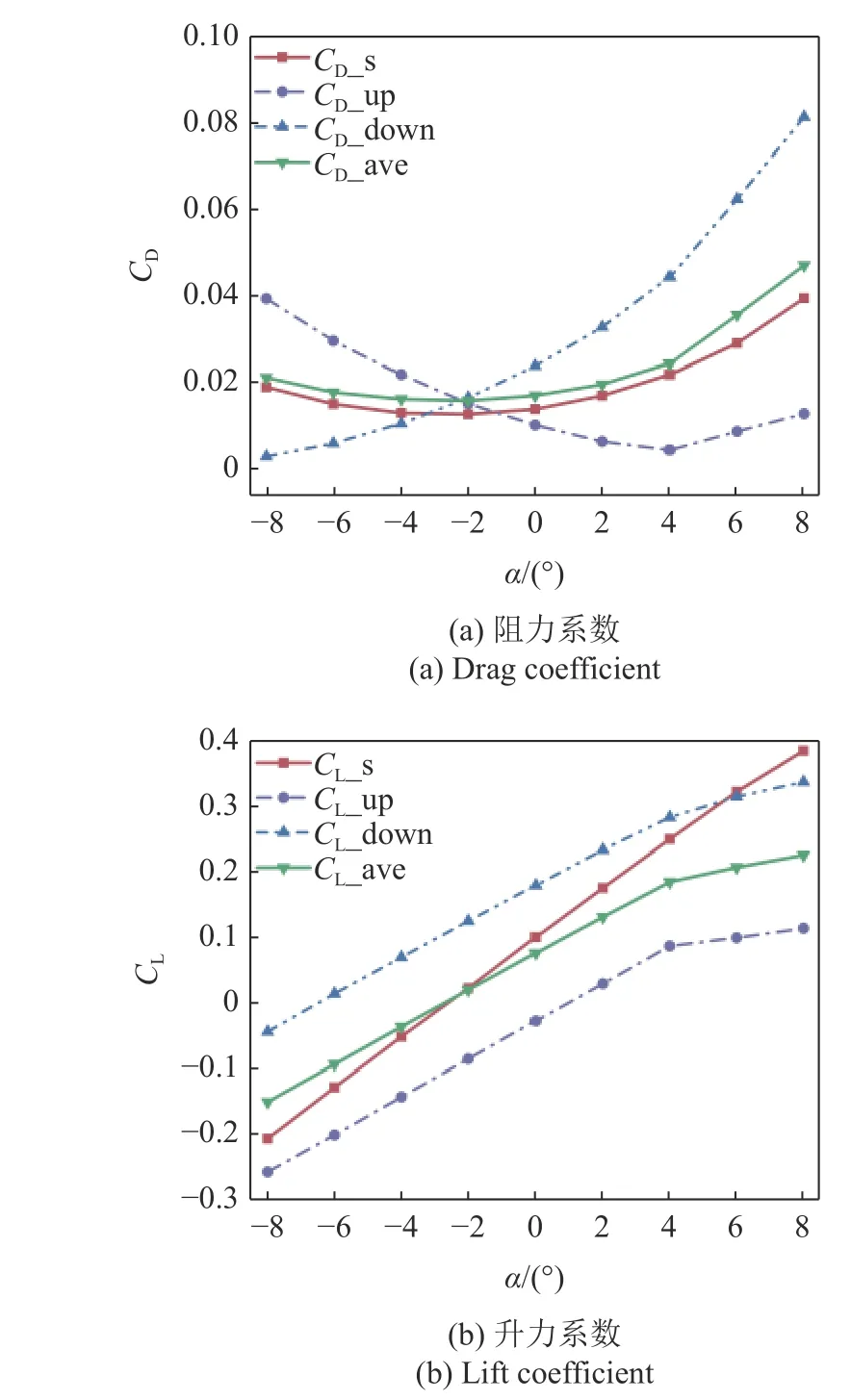
圖7 0.5TL 垂向間距時(shí)不同攻角下的阻力/升力系數(shù)Fig.7 Drag/lift coefficient at different attack angles at 0.5TL vertical distance

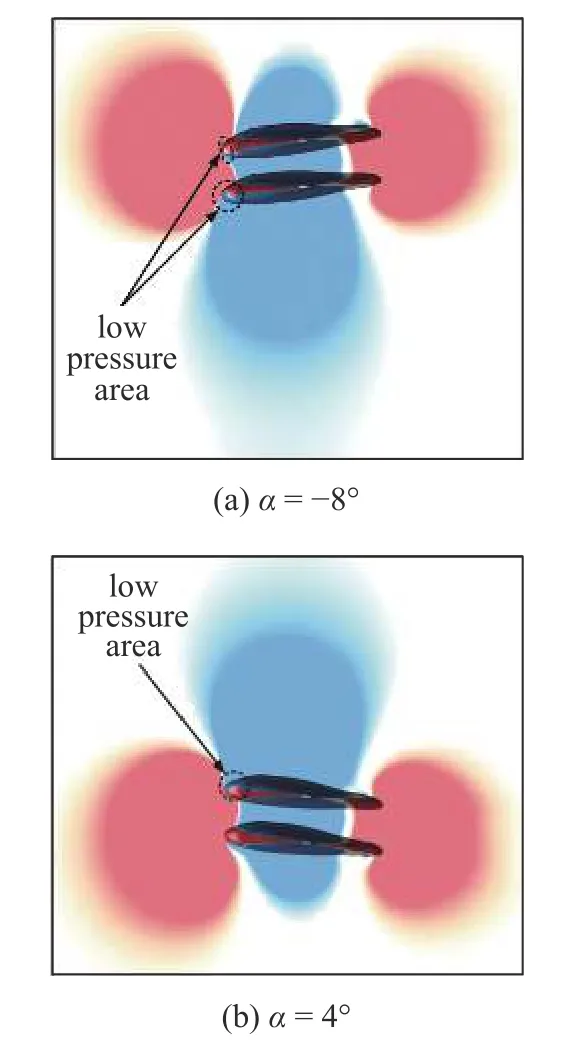
圖8 0.5TL 垂向間距時(shí)不同攻角下的壓力云圖Fig.8 Pressure diagram at different attack angles at 0.5TL vertical distance

3.3 垂向間距0.75TL

同前,圖9 展示了當(dāng)垂向間距為0.75TL時(shí),上(下) 方蝠鲼阻力(升力) 系數(shù)、系統(tǒng)平均阻力(升力)系數(shù)以及單體蝠鲼阻力(升力)系數(shù)隨攻角變化的改變情況.由圖9(a)可以看出,系統(tǒng)平均阻力更加接近單體滑翔時(shí)所受到的阻力,上、下方蝠鲼的阻力差值也減小,說明垂向間距的增大,集群中單體間相互影響降低.同樣,我們將?8°,4°時(shí)的壓力云圖繪制在了圖10 中,從圖10(a)可以看出,在以負(fù)攻角滑翔時(shí),上方蝠鲼頭部的中下部低壓區(qū)面積擴(kuò)大,使得上方蝠鲼阻力進(jìn)一步降低(見圖9).從圖10(b)可以發(fā)現(xiàn)以正攻角滑翔時(shí),下方蝠鲼頭部開始出現(xiàn)低壓區(qū),使得下方蝠鲼的阻力減小(見圖9).由此可以看出,隨著垂向距離的增加,集群中各單體間的相互作用減弱,系統(tǒng)平均阻力和單體滑翔阻力逐步接近.由圖9(b)可以看出,系統(tǒng)平均升力變化不大,上下兩蝠鲼升力差值進(jìn)一步減小.

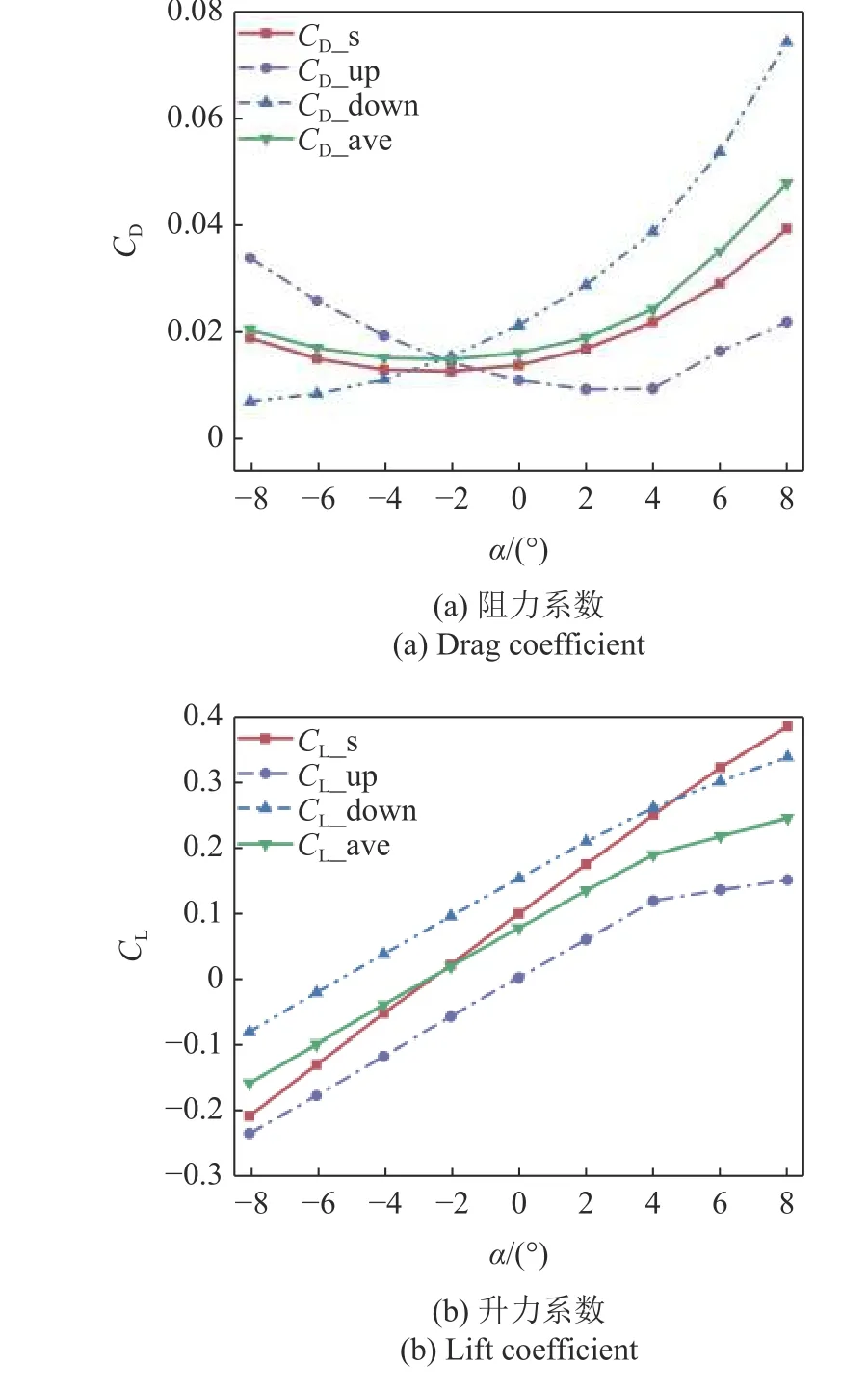
圖9 0.75TL 垂向間距時(shí)不同攻角下的阻力/升力系數(shù)Fig.9 Drag/lift coefficient at different attack angles at 0.75TL vertical distance

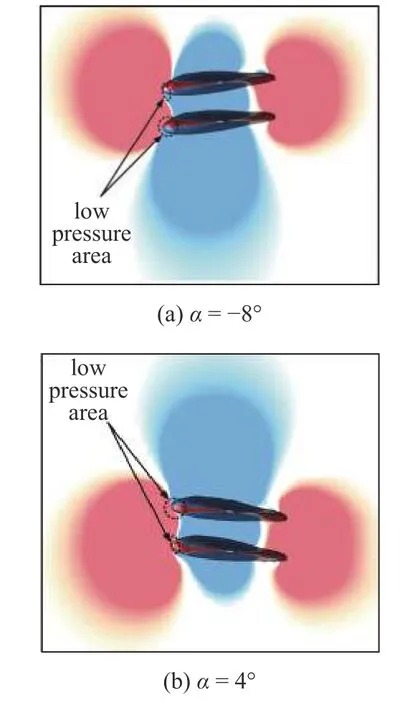
圖10 0.75TL 垂向間距時(shí)不同攻角下的壓力云圖Fig.10 Pressure diagram at different attack angles at 0.75TL vertical distance

3.4 垂向間距1TL

同前,圖11 展示了當(dāng)垂向間距為1TL時(shí),上(下)方蝠鲼阻力系數(shù)、系統(tǒng)平均阻力系數(shù)以及單體蝠鲼阻力系數(shù)隨攻角變化的改變情況.由圖11(a)可以看出,當(dāng)攻角在?8°,?4°時(shí),系統(tǒng)平均阻力與單體滑翔時(shí)所受到的阻力幾乎保持一致,上、下方蝠鲼的阻力差值也進(jìn)一步減小,集群中單體間相互影響進(jìn)一步削弱.由圖11(b)可以看出,系統(tǒng)平均升力變化不大,隨著垂向距離的增加,上下兩蝠鲼的升力差值也隨之減小.我們將?8°,4°時(shí)的壓力/速度云圖繪制在了圖12 中,從圖12(a)和圖12(b)可以看出,當(dāng)以負(fù)攻角滑翔時(shí),上方蝠鲼頭部的中下部低壓區(qū)面積擴(kuò)大,使得上方蝠鲼阻力進(jìn)一步降低,類似的,當(dāng)以正攻角滑翔時(shí),下方蝠鲼頭部的低壓區(qū)面積也有所增加,因此此時(shí)下方蝠鲼的阻力也隨之減小.由圖12(c)可以看出隨著間距的增大,上下兩蝠鲼的速度云圖幾乎保持一致,集群滑翔對集群中各單體的速度場影響減弱.

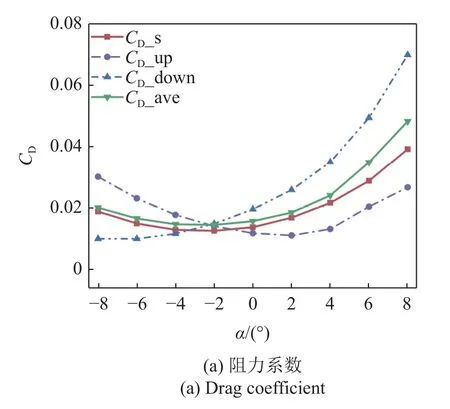
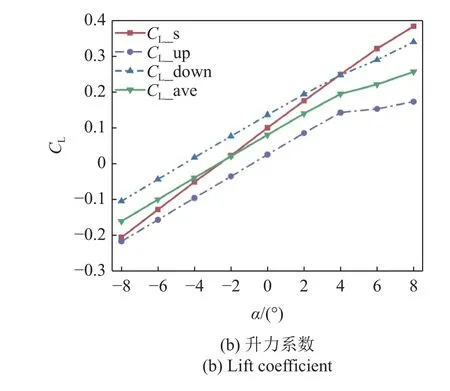
圖11 1TL 垂向間距時(shí)不同攻角下的阻力/升力系數(shù)Fig.11 Drag/lift coefficient at different attack angles at 1TL vertical distance

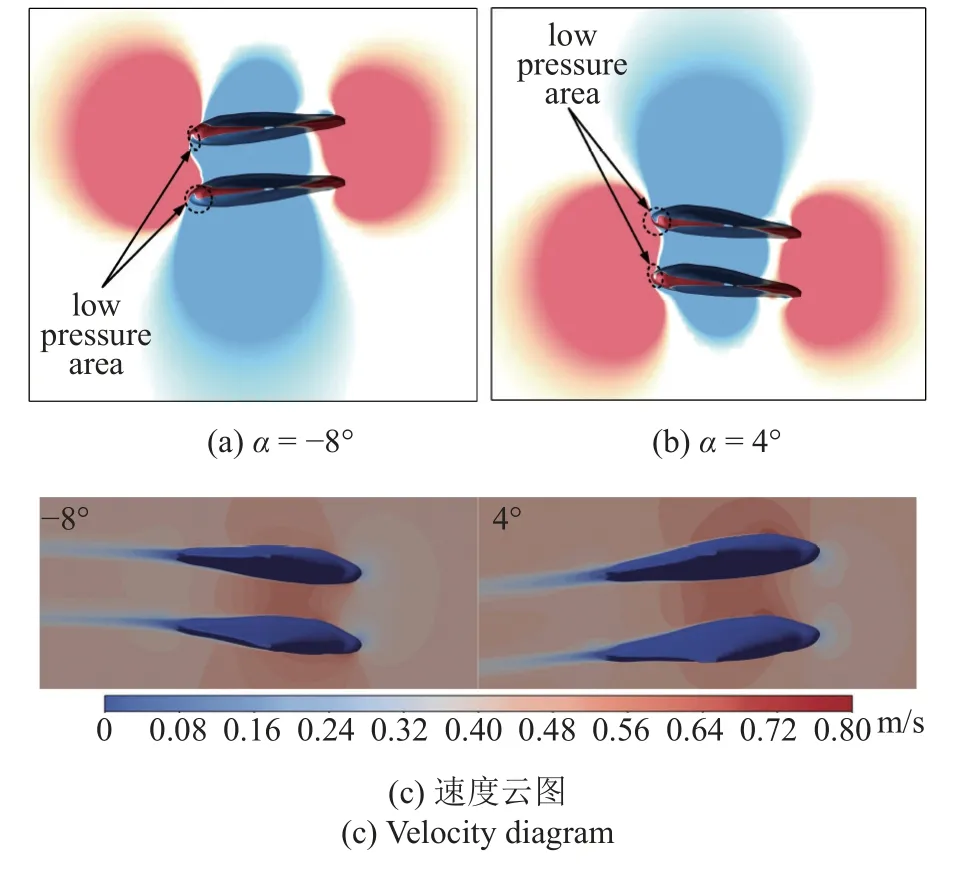
圖12 1TL 垂向間距時(shí)不同攻角下的壓力/速度云圖Fig.12 Pressure/velocity diagram at different attack angles at 1TL vertical distance

4 結(jié)論

本文借助Fluent 軟件對沿垂向分布的雙蝠鲼集群滑翔狀態(tài)進(jìn)行了數(shù)值仿真,得到了升力、阻力系數(shù)曲線,并結(jié)合壓力云圖進(jìn)行分析,得到了如下結(jié)論.

(1)系統(tǒng)平均升力受垂向間距影響較小,當(dāng)滑翔攻角小于?2°時(shí),系統(tǒng)平均升力大于單體滑翔時(shí)的升力;當(dāng)滑翔攻角大于?2°時(shí),系統(tǒng)平均升力小于單體滑翔時(shí)的升力;當(dāng)滑翔攻角為?2°時(shí),系統(tǒng)平均升力與單體滑翔升力接近.下方蝠鲼升力總大于上方蝠鲼,但隨著垂向間距增加,上下兩蝠鲼升力差距減小.

(2)雙蝠鲼沿垂向分布在攻角范圍為?8°～8°進(jìn)行集群滑翔時(shí)未能發(fā)現(xiàn)系統(tǒng)平均阻力低于單體滑翔時(shí)所受阻力的情況,但隨著垂向間距的增加,單體間相互影響降低,系統(tǒng)平均阻力趨近于單體滑翔阻力.

(3)系統(tǒng)平均阻力雖未能發(fā)現(xiàn)減阻效果,但集群中單體能從集群滑翔中獲得減阻收益.當(dāng)雙蝠鲼以負(fù)攻角集群滑翔時(shí),下方蝠鲼獲得減阻收益,且垂向間距越小,獲得的減阻效果越明顯;當(dāng)以正攻角集群滑翔時(shí),則是上方蝠鲼獲得減阻收益.

(4) 雙蝠鲼集群滑翔過程中各單體阻力(升力)表現(xiàn)的差異性主要來源于蝠鲼頭部、中腹部壓力區(qū)的變化,垂向間距的變化改變了壓力區(qū)分布,從現(xiàn)有結(jié)果可以看出隨著垂向間距的進(jìn)一步加大,上(下)蝠鲼壓力分布會(huì)趨于一致.