平面冪律塑性I型裂紋尖端應(yīng)力場全解1)

王志強(qiáng) 蔡力勛 黃茂波

(西南交通大學(xué)力學(xué)與航空航天學(xué)院,應(yīng)用力學(xué)與結(jié)構(gòu)安全四川省重點(diǎn)實(shí)驗(yàn)室,成都 610031)

引言

在航空航天、船舶、核電和化工等工程中,裂紋構(gòu)件的裂紋尖端應(yīng)力場與斷裂強(qiáng)度是結(jié)構(gòu)安全評(píng)價(jià)的重要基礎(chǔ).

Cherepanov[1]和Rice[2]分別在1967 年和1968年針對含I 型裂紋無限體各自獨(dú)立提出與裂紋尖端環(huán)向積分路徑無關(guān)的J積分.隨后,Hutchinson[3]、Rice 等[4](HRR) 針對冪律硬化材料,基于J積分和塑性解析求解在理論上給出描述裂尖應(yīng)力場的HRR 奇異解,該解關(guān)于角度分布的解析描述一直未得到解決.1983 年,Shih[5]考慮冪律塑性應(yīng)力?應(yīng)變關(guān)系,通過有限元分析計(jì)算了HRR 解中的積分常數(shù)IN和無量綱角度函數(shù),相關(guān)結(jié)果均由數(shù)值表格形式給出.1991 年,Betegon 等[6]利用邊界層方法研究小范圍屈服條件下不同T應(yīng)力(T11,作用于裂紋面且垂直于裂紋前沿的應(yīng)力分量)對彈塑性應(yīng)力場的影響,提出J-T11方法,該方法以T11作為表征裂尖約束程度的彈性參量用于描述I 型裂紋有限尺寸試樣的彈塑性裂尖場.后繼研究[7-9]表明,具有彈性屬性的T應(yīng)力不適用于大范圍或全范圍屈服條件.1991 年,對于中心裂紋板和單邊裂紋彎曲兩個(gè)有限幾何尺寸試樣,O’Dowd等[10-11]為反映有限尺寸對裂尖場的幾何約束效應(yīng),考慮在HRR 場基礎(chǔ)上進(jìn)行約束補(bǔ)償,提出J-Q方法,該方法對不同材料和試樣的不同幾何尺寸,完全依賴有限元分析,所獲得Q值有不同結(jié)果,無普適性Q方程,應(yīng)用不便.1986 年Li 等[12]提出含高次展開項(xiàng)的冪律塑性漸進(jìn)解作為HRR 場約束補(bǔ)償項(xiàng)的新思路,1991 年Sharma 等[7]及1993 年Yang 等[13]采用一次高階漸近項(xiàng)作為HRR 場補(bǔ)償項(xiàng)提出了裂尖場描述模型,該模型通過復(fù)雜數(shù)值分析僅對特定材料和幾何工況給出漸進(jìn)解參數(shù),相較HRR 場描述精度上有了提升,不過,對于不同材料和不同幾何工況需給出不同漸進(jìn)解參數(shù),普適性仍然不足.Yang等[8,14]基于裂紋尖端應(yīng)力場的3 項(xiàng)漸近展開式,給出了第二和第三展開項(xiàng)的系數(shù)之間的近似關(guān)系,提出了J-A2理論.Nikishkov 等[9,15]采用類似方法,提出J-A理論,本質(zhì)上和J-A2理論一樣[16-17].隨后,Ding 等[18-19]進(jìn)行廣泛的有限元分析,獲得經(jīng)驗(yàn)方程,預(yù)測約束參數(shù)A,Q,A2等參數(shù).上述應(yīng)力漸進(jìn)解均無關(guān)于角度的描述函數(shù).事實(shí)上,任何復(fù)雜函數(shù)關(guān)系都可以由不同函數(shù),如高階級(jí)數(shù)函數(shù)、特殊函數(shù)等函數(shù)同時(shí)表征,描述形式并非唯一.Ji 等[20-21]通過數(shù)值分析提出特殊的指數(shù)函數(shù)來表征特定材料具有奇異性的彈塑性應(yīng)力場,雖然該修正的奇異性指數(shù)并沒有適用于不同材料和幾何條件的統(tǒng)一表達(dá)式,但這是針對塑性裂尖奇異場研究提出的一個(gè)重要概念和新方法.

此外,也有學(xué)者在研究斷裂韌性時(shí)嘗試將裂尖塑性區(qū)與裂尖約束聯(lián)系起來.Anderson 等[22]提出A-D 法,即用裂尖前最大正應(yīng)力σ1與屈服應(yīng)力σy的比值來表征約束,比值越大,約束越大.Mostafavi等[23-26]對A-D 法進(jìn)行了改進(jìn),用試樣或結(jié)構(gòu)斷裂時(shí)的裂尖塑性區(qū)面積Ac與標(biāo)準(zhǔn)高約束平面應(yīng)變斷裂韌性試樣斷裂時(shí)的裂尖塑性區(qū)面積Assy(參考塑性區(qū)面積)的比值 φ來表征約束水平來表征約束水平,用φ可以將任何約束(不同的面內(nèi)和面外約束)水平下的斷裂韌性JIC試驗(yàn)數(shù)據(jù)關(guān)聯(lián)起來,建立一致性的斷裂韌性與約束的關(guān)聯(lián)線.

本文考慮冪律塑性本構(gòu)關(guān)系,基于能量密度等效原理[27-29]和量綱分析提出具有中值能量密度的代表性體積單元 (representative volume element,RVE)的等效應(yīng)力(σM)解析方程,以能量密度等效體積單元的應(yīng)力因子為應(yīng)力特征量,提出平面冪律塑性I 型裂紋尖端應(yīng)力場半解析模型.針對有限平面應(yīng)變和平面應(yīng)力緊湊拉伸(compact tension,CT)試樣和單邊裂紋彎曲(single edge bend,SEB)試樣,給出應(yīng)力場半解析模型參數(shù)的確定方法,并進(jìn)行數(shù)值分析的模型驗(yàn)證.

1 理論模型

1.1 等效應(yīng)力解析方程

假設(shè)延性材料均勻連續(xù)、各向同性,對于受單向加載的任意構(gòu)元(見圖1),Chen 等[27-29]基于復(fù)雜應(yīng)力與單軸應(yīng)力下 RVE 應(yīng)變能密度等效(圖1中任意A點(diǎn)RVE)及應(yīng)變能密度中值等效(圖1 中值M點(diǎn)RVE),提出彈塑性應(yīng)變能U控制方程為

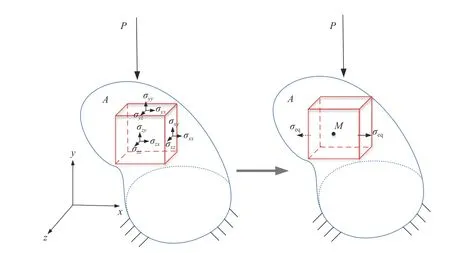
圖1 能量密度等效示意圖Fig.1 Schematic diagram of energy density equivalence

式中,Veff為有效變形域體積,εeq?M為RVE 等效應(yīng)變.

冪律塑性條件下,設(shè)材料應(yīng)力應(yīng)變關(guān)系符合冪律

式中,εp?eq為等效塑性應(yīng)變,σeq為等效應(yīng)力,K為材料的應(yīng)變硬化系數(shù),N為應(yīng)力硬化指數(shù).進(jìn)一步假定Veff,εp?eq與加載線位移hp之間符合冪律關(guān)系

式中,特征體積V*為A*h*,A*為特征面積;h*為特征位移;k1和k2分別為有效體積系數(shù)和有效體積指數(shù),k3和k4分別為等效塑性應(yīng)變系數(shù)和等效塑性應(yīng)變指數(shù).

由式(1)、式(2)和式(3)得到冪律塑性應(yīng)變能Up控制方程

根據(jù)文獻(xiàn)[27-28],受單向加載構(gòu)元的載荷?位移關(guān)系表示為

式中,P為載荷,P*為特征載荷,ζp和mp分別為冪律塑性條件下的無量綱載荷?位移關(guān)系系數(shù)和指數(shù),m為體積折減系數(shù).

能量密度中值點(diǎn)RVE 的等效應(yīng)力σM與載荷P及加載線位移hp與構(gòu)元特征尺寸分別構(gòu)成相似判據(jù)π1,π2,設(shè)為

假定π1和π2之間關(guān)系符合冪律

式中,k5和k6分別為等效應(yīng)力系數(shù)和等效應(yīng)力指數(shù).由式(6)和式(7)可得

聯(lián)立式(4)和式(8),整理可得

在準(zhǔn)靜態(tài)加載和冪律塑性條件下,根據(jù)功-能原理,載荷對構(gòu)元試樣所做的功等于構(gòu)元試樣的變形能(U),進(jìn)而由上式可得

將式(5)的載荷P代入式(10)中整理可得

上式等號(hào)左右項(xiàng)積分整理可得

考慮到等號(hào)右端項(xiàng)為常數(shù),則等號(hào)左端項(xiàng)的無量綱變量hp/h*的指數(shù)項(xiàng)必為0,則1?(k2+k4+k6)=0,此時(shí)右端項(xiàng)必為1,進(jìn)而可得

結(jié)合冪律應(yīng)變式(4)、關(guān)于P與hp的無量綱式(8)及k5,k6表達(dá)式(13),可得σM解析方程,定義該應(yīng)力為應(yīng)力因子

1.2 平面I 型裂紋尖端應(yīng)力場半解析模型

對于I 型裂紋構(gòu)元,有效變形體積在加載過程中保持不變,則式(4)中k2為0;由文獻(xiàn)[30]可知冪律塑性條件下中值點(diǎn)RVE 等效應(yīng)變與試樣加載線位移之間呈線性關(guān)系,即,式(4)中k4為1.則k5=(k1k3)?1,k6=0.進(jìn)一步由式(4)、式(5) RVE 等效應(yīng)力的解析方程可簡化為

對于有限尺寸試樣,裂紋尖端應(yīng)力場不再符合HRR 解.考慮HRR 解的奇異性,對裂尖應(yīng)力,以應(yīng)力因子σM作為特征應(yīng)力,則基于特征應(yīng)力的無量綱裂尖應(yīng)力表為

式中,當(dāng)sub 為eq 時(shí),σeq是等效應(yīng)力,當(dāng)sub 為ij時(shí),σij是應(yīng)力張量(ij=11 時(shí)為rr,ij=22 時(shí)為θθ,ij=12 時(shí)為rθ),σM是特征應(yīng)力,L是特征長度(通常取為1 mm),f和λ為關(guān)于N與θ的函數(shù),m為試樣尺寸a/W的綜合指數(shù).

考慮到HRR 場奇異性指數(shù)為1/(N+1),對分子、分母各疊加一個(gè)關(guān)于θ增量β’sub,即(1+β’sub)/(N+1+β’sub),可進(jìn)一步假設(shè)fsub=βsub/(N+βsub),βsub=1+β’sub,βsub為與三角函數(shù)相關(guān)的特殊函數(shù),即

式中,dsubp(p=0,1,2,3)為待定參數(shù).

有限元計(jì)算表明冪律塑性條件下裂尖等效應(yīng)力等值線在平面應(yīng)變和平面應(yīng)力下分別具有蝶翅輪廓和扇貝輪廓的特征,為描述這兩類特殊的等應(yīng)力輪廓線,設(shè)應(yīng)力分布系數(shù)λsub為三角特殊函數(shù)

式中,psubk(k=0,1,2)與qsubm(m=0,1,2,3)為待定參數(shù),psubk(k=0,1,2)與N相關(guān),csubk(k=0,1,2),bsubk(k=0,1,2) 為psubk的待定參數(shù).

修正綜合指數(shù)msub與N相關(guān),假設(shè)

式中,msub0和msub1為待定參數(shù).

聯(lián)立式(16)～ 式(19)可得平面冪律塑性I 型裂紋尖端應(yīng)力場半解析模型

若式(16) 中 λeq·(L/r)feq取為不同程度常數(shù)C,則由式(17)、式(18)有

選擇合適的級(jí)數(shù)項(xiàng)數(shù)和相應(yīng)參數(shù),可在數(shù)學(xué)上使上述函數(shù)能恰當(dāng)描述蝶翅輪廓式或扇貝輪廓式等應(yīng)力線,進(jìn)而由式(20)可推導(dǎo)出平面I 型裂紋有限尺寸試樣等效應(yīng)力等值線表達(dá)式

2 有限元分析

2.1 分析條件

本文采用有限元分析(finite element analysis,FEA)軟件ANSYS19.0 對CT 試樣和SEB 試樣進(jìn)行研究,本文所針對CT 試樣和SEB 試樣的建模參數(shù)標(biāo)定及模型驗(yàn)證都針對有限尺寸試樣.幾何構(gòu)型如圖2 所示,a為裂紋長度,b為裂紋剩余韌帶長度.

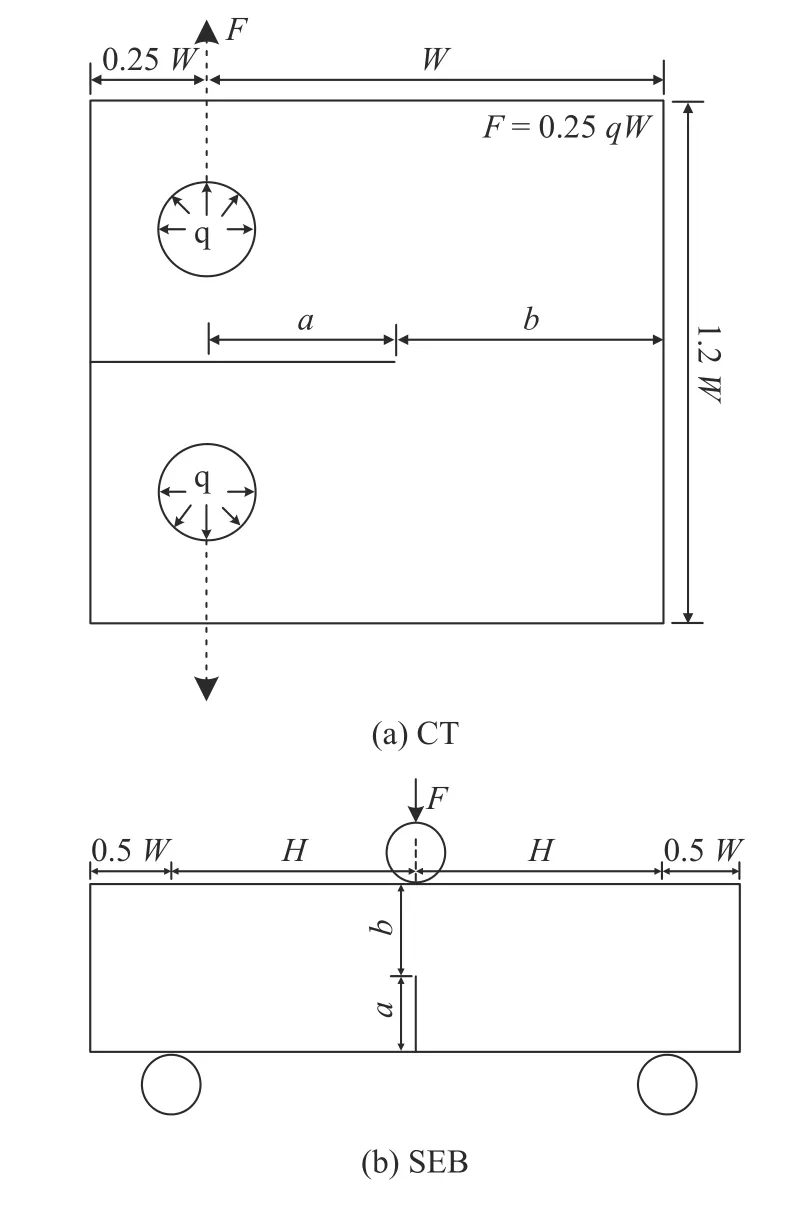
圖2 試樣示意圖Fig.2 Schematic diagram of specimens

由于對稱性,圖3 給出了試樣的有限元分析的1/2模型,CT 試樣的寬度W為50 mm,SEB 試樣的寬度W為20 mm,其跨度H和寬度W之比H/W為2.裂紋尖端采用1/4 節(jié)點(diǎn)奇異單元(KSCON),其余部分均采用4 節(jié)點(diǎn)單元(Plane182),裂紋剩余韌帶部分施加對稱約束邊界條件.CT 試樣采用銷釘孔上半圓內(nèi)邊緣施加法向等效均布?jí)狠d荷(合力F即為試樣的載荷,F=0.25qW),考慮銷釘加載時(shí)加載孔X方向固定,對加載孔上方接觸點(diǎn)施加X向約束;SEB 試樣采用壓頭位移加載,壓頭(或加載輥)均采用Target169單元,構(gòu)元試樣表面均采用contact 172單元.

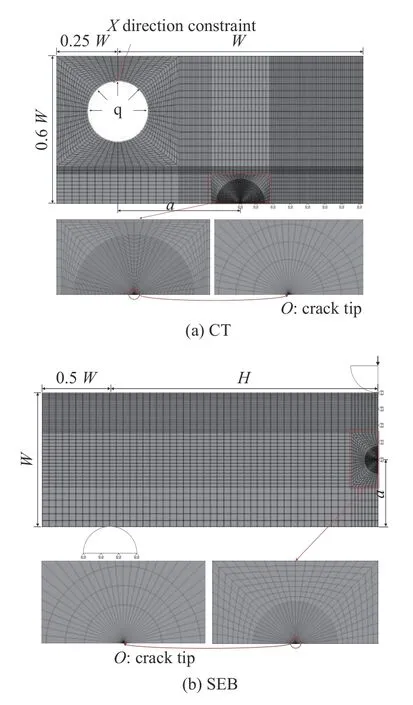
圖3 FEA 模型圖Fig.3 FEA model of specimens

2.2 FEA 模型驗(yàn)證

為在網(wǎng)格模型設(shè)計(jì)中選用合適網(wǎng)格密度,需考察裂尖附近不同網(wǎng)格密度對 FEA 結(jié)果的影響,針對有限平面應(yīng)變(plane strain)、平面應(yīng)力(plane stress)條件的CT 試樣,有限元分析預(yù)設(shè)材料本構(gòu)關(guān)系為冪律,即式(2),預(yù)設(shè)K:1000 MPa,N:10,a/W: 0.5 完成冪律塑性分析,考察裂尖附近不同網(wǎng)格密度下的應(yīng)力分布.定義圖3 中所示距裂尖5 mm扇形范圍內(nèi)單元尺寸為 1 倍網(wǎng)格密度(扇形單元徑向尺寸S為0.08 mm),2 倍、4 倍、8 倍網(wǎng)格密度定義為對裂尖扇形區(qū)網(wǎng)格加密為1 倍網(wǎng)格密度的相應(yīng)倍數(shù)(扇形單元徑向尺寸S相應(yīng)為0.04 mm,0.02 mm,0.01 mm).圖4 和圖5 中圖例的標(biāo)記符號(hào)NE和NN分別表示不同密度下扇形網(wǎng)格區(qū)沿徑向單元總數(shù)和節(jié)點(diǎn)數(shù).圖4 和圖5 分別給出了有限平面應(yīng)變和平面應(yīng)力條件下不同網(wǎng)格密度CT 試樣 的FEA 獲取的載荷位移曲線和裂尖等效應(yīng)力分布,結(jié)果表明,采用 1 倍網(wǎng)格密度時(shí)已經(jīng)滿足計(jì)算要求.

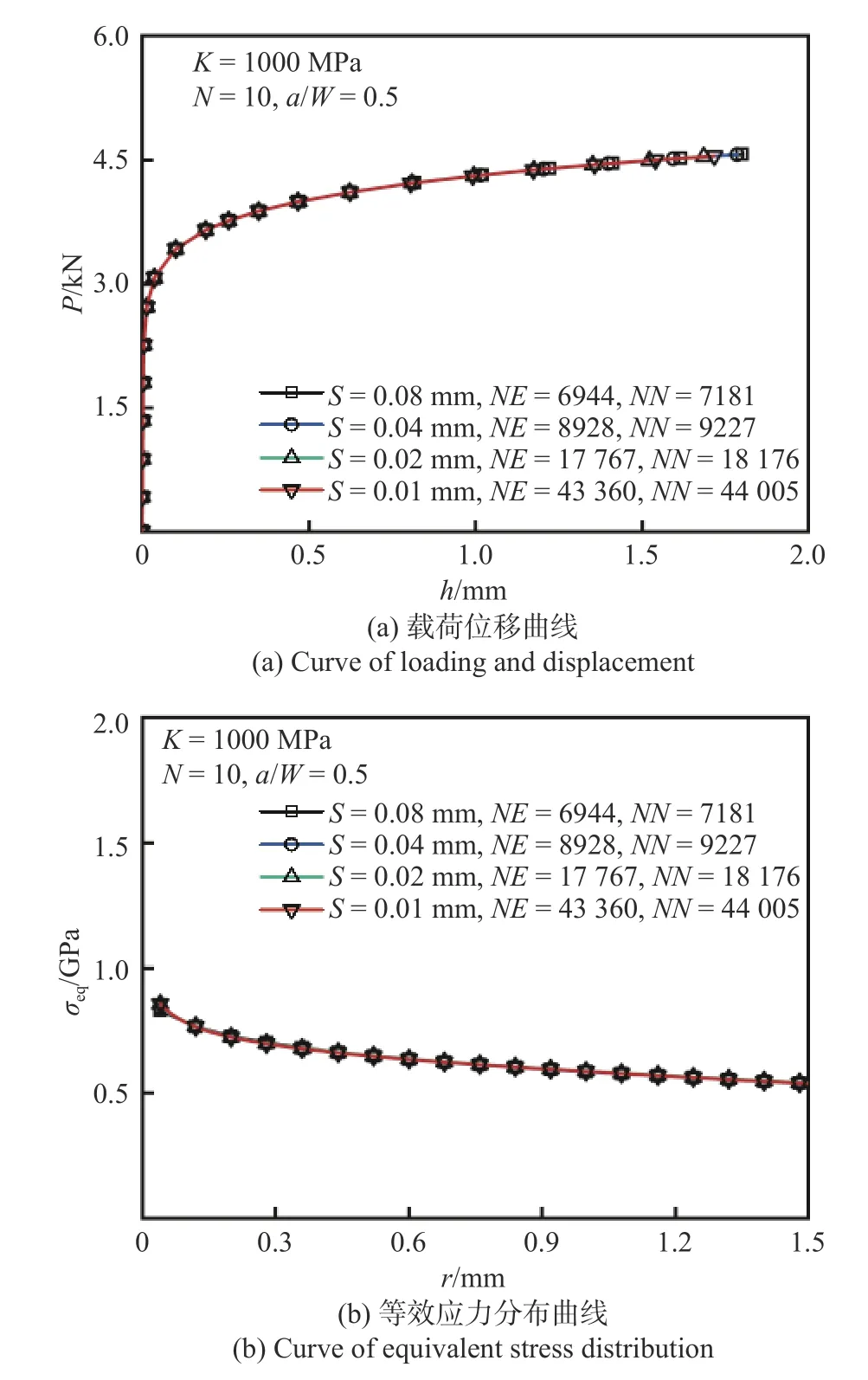
圖4 平面應(yīng)變條件下裂尖附近網(wǎng)格密度對FEA 結(jié)果的影響Fig.4 Effects of element meshing size around the crack tip on the FEA results under plane strain conditions

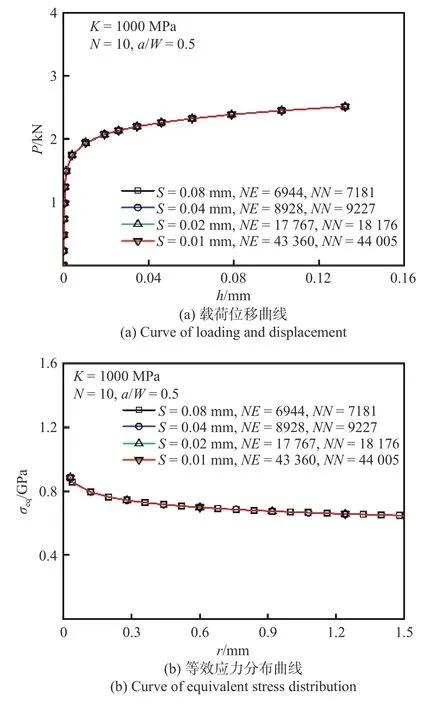
圖5 平面應(yīng)力條件下裂尖附近網(wǎng)格密度對FEA 結(jié)果的影響Fig.5 Effects of element meshing size around the crack tip on the FEA results under plane stress conditions

2.3 模型參數(shù)的確定

為了更加了解式(20)的特征,以下部分以平面應(yīng)變條件下CT 試樣的應(yīng)力分布為例,給出了參數(shù)確定方法.

2.3.1 綜合指數(shù)m和修正綜合指數(shù)msub

選取無量綱裂紋長度a/W為0.45～ 0.75(間隔0.05),應(yīng)變硬化系數(shù)K為1000 MPa,應(yīng)力硬化指數(shù)N分別為12,10,6 和4,在冪律塑性條件下進(jìn)行計(jì)算.文獻(xiàn)[30]給出了CT 和SEB 試樣在平面應(yīng)變條件下的體積折減系數(shù)m與參數(shù)k1～k4,進(jìn)而通過式(15)得到k5,用同樣方法可標(biāo)定出平面應(yīng)力條件下體積折減系數(shù)m與等效應(yīng)力系數(shù)k5,方程(15)參數(shù)如表1 所示.

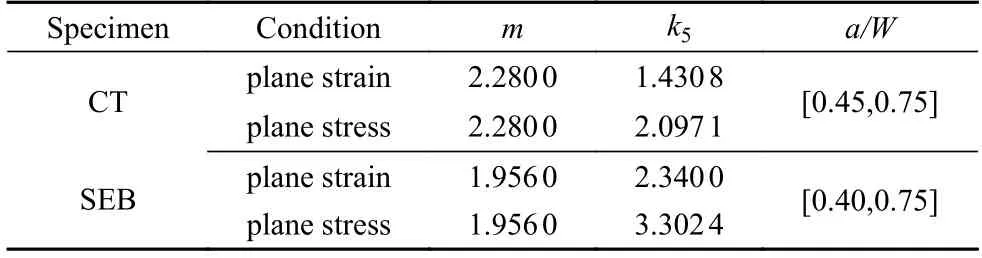
表1 方程(15)模型參數(shù)Table 1 Parameters of Eq.(15)

進(jìn)一步以應(yīng)力因子σM為特征量,對不同無量綱裂紋長度a/W與應(yīng)力硬化指數(shù)N下無量綱應(yīng)力σsub/σM～r/L冪律擬合得到系數(shù)λsub,在給定應(yīng)力硬化指數(shù)N時(shí),將系數(shù)λsub與無量綱裂紋長度(1?a/W)冪律擬合得到msub,接著在不同N條件擬合出式(19)的待定參數(shù)msub0和msub1.圖6 為修正綜合指數(shù)參數(shù)標(biāo)定過程,表2 給出了CT 和SEB 試樣分別在平面應(yīng)變和平面應(yīng)力條件下的待定參數(shù)msub0和msub1.在以下研究中,以σM作為特征應(yīng)力,獲得裂尖的無量綱應(yīng)力分布分析參數(shù)βsub和λsub.

圖6 參數(shù)標(biāo)定Fig.6 Calibration parameter

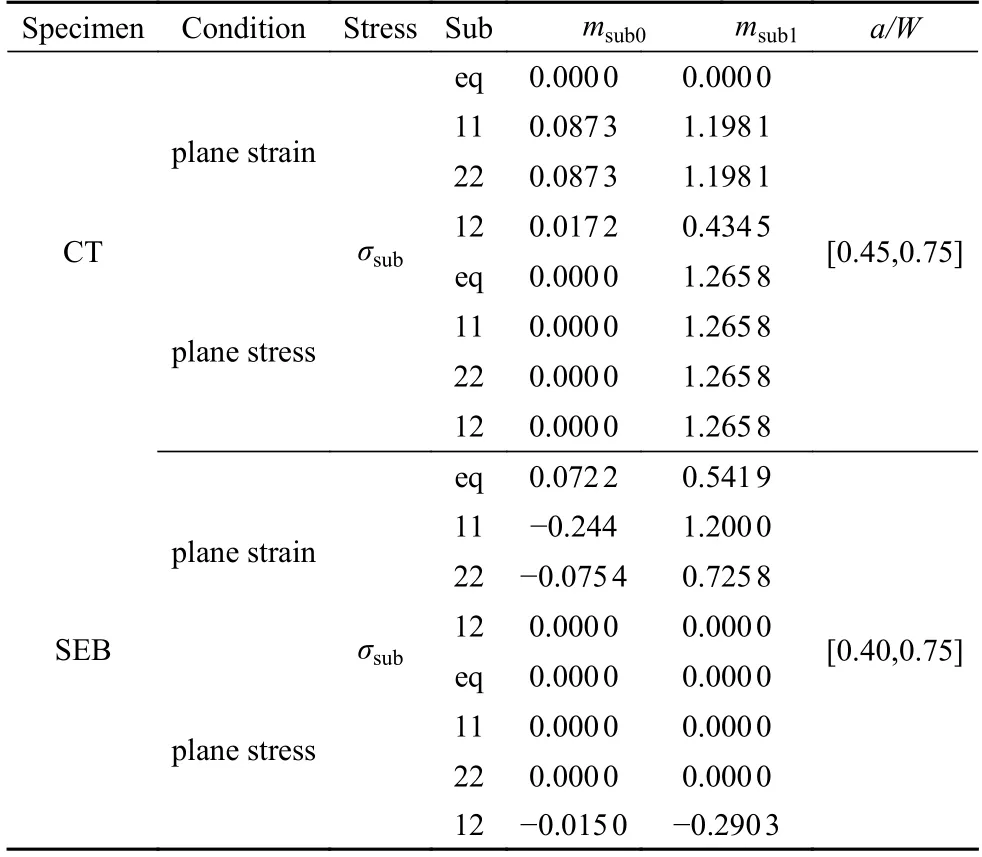
表2 方程(19)參數(shù)Table 2 Parameters of Eq.(19)

2.3.2 奇異性指數(shù)fsub及其參數(shù)βsub

參考常用材料,選取無量綱裂紋長度a/W為0.6,應(yīng)變硬化系數(shù)K為1000 MPa,應(yīng)力硬化指數(shù)N分別為12,10,6 和4,在冪律塑性條件下進(jìn)行計(jì)算.在距離裂紋尖端0.06b范圍內(nèi)的應(yīng)力分布可用關(guān)于L/r的冪函數(shù)進(jìn)行描述,其奇異性分布指數(shù)fsub可由回歸確定;考慮到應(yīng)力的奇異性主要體現(xiàn)在裂紋尖端附近的右扇形區(qū),故主要關(guān)注應(yīng)力在θ=0 到θ=π/2 的等效應(yīng)力分布,在平面應(yīng)變條件下得到各個(gè)角度的fsub和對應(yīng)的βsub.參數(shù)βsub與θ關(guān)系如圖7 所示,由(17)可得三角函數(shù)關(guān)系如下

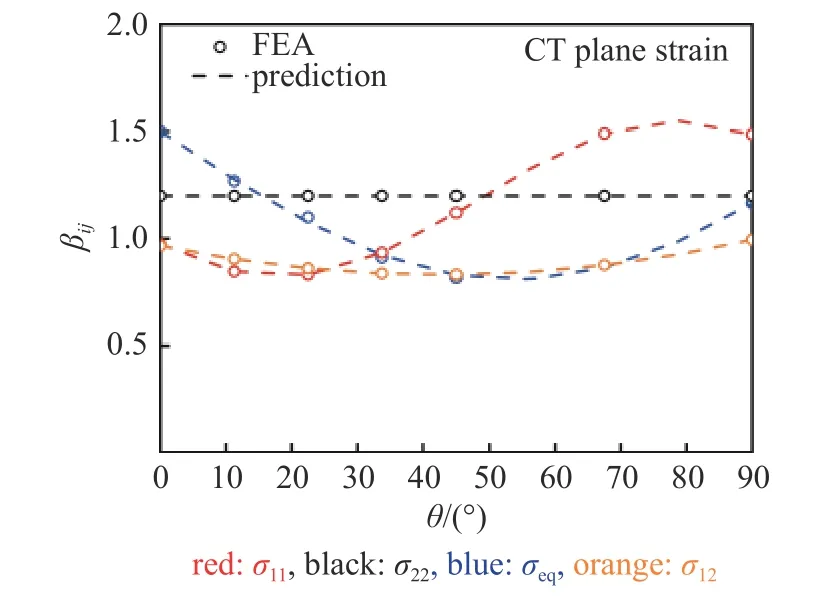
圖7 角度θ 對β 影響Fig.7 Effect of θ on β

式中,dsubp(p=0,1,2,3)為待定參數(shù).

類似可得到平面條件下βsub與θ的關(guān)系,表3給出了CT 和SEB 試樣分別在平面應(yīng)變和平面應(yīng)力條件下的參數(shù)dsubp(p=1,2,3,4)

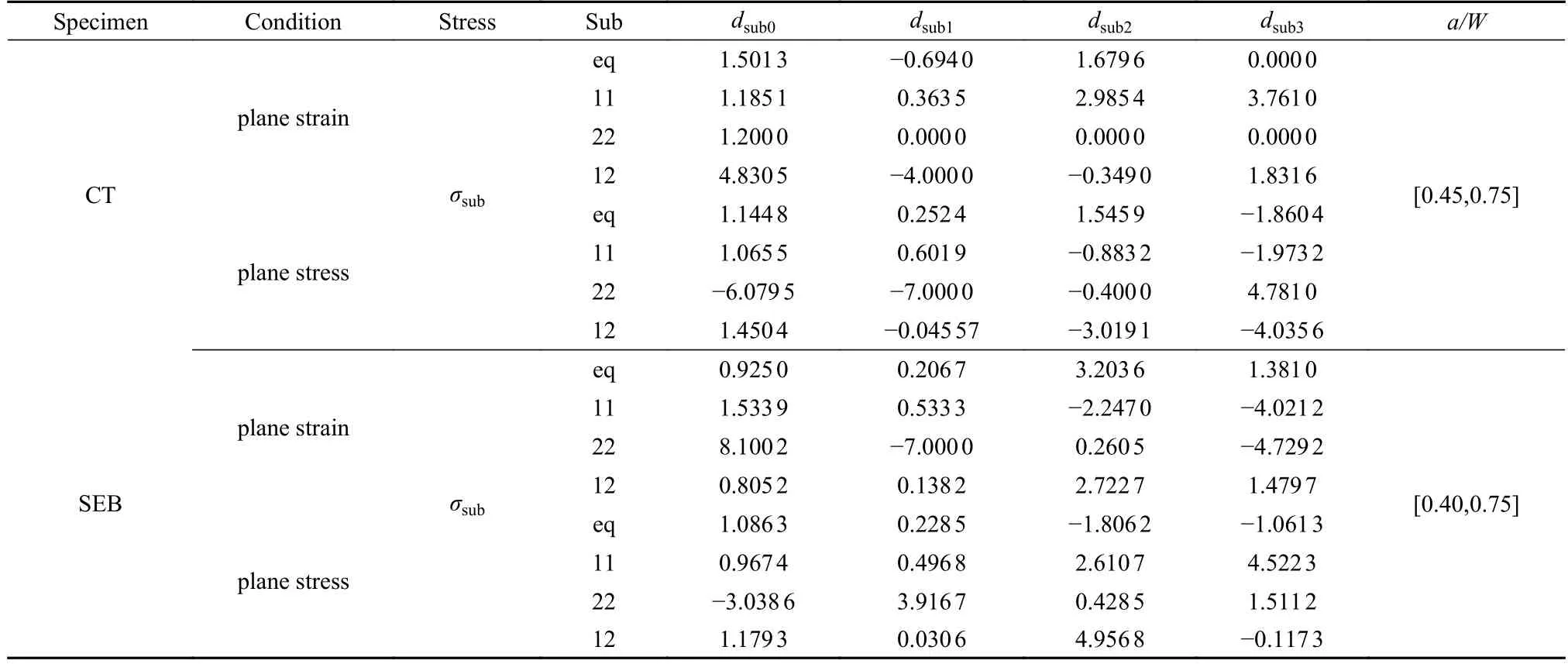
表3 方程(23)模型參數(shù)Table 3 Parameters of Eq.(23)

2.3.3 無量綱應(yīng)力分布系數(shù)λsub

為考慮各類因素對無量綱應(yīng)力分布系數(shù)λsub的影響,以平面應(yīng)變條件下試樣裂紋面(θ=0)的應(yīng)力分布為例,將應(yīng)力硬化指數(shù)N固定為10,以σM作為特征應(yīng)力,獲得裂尖的無量綱應(yīng)力分布,以此分析λsub.圖8 給出了載荷P和應(yīng)力硬化系數(shù)K對λsub的影響,表明無量綱應(yīng)力分布系數(shù)λsub與載荷P和應(yīng)力硬化系數(shù)K無關(guān).

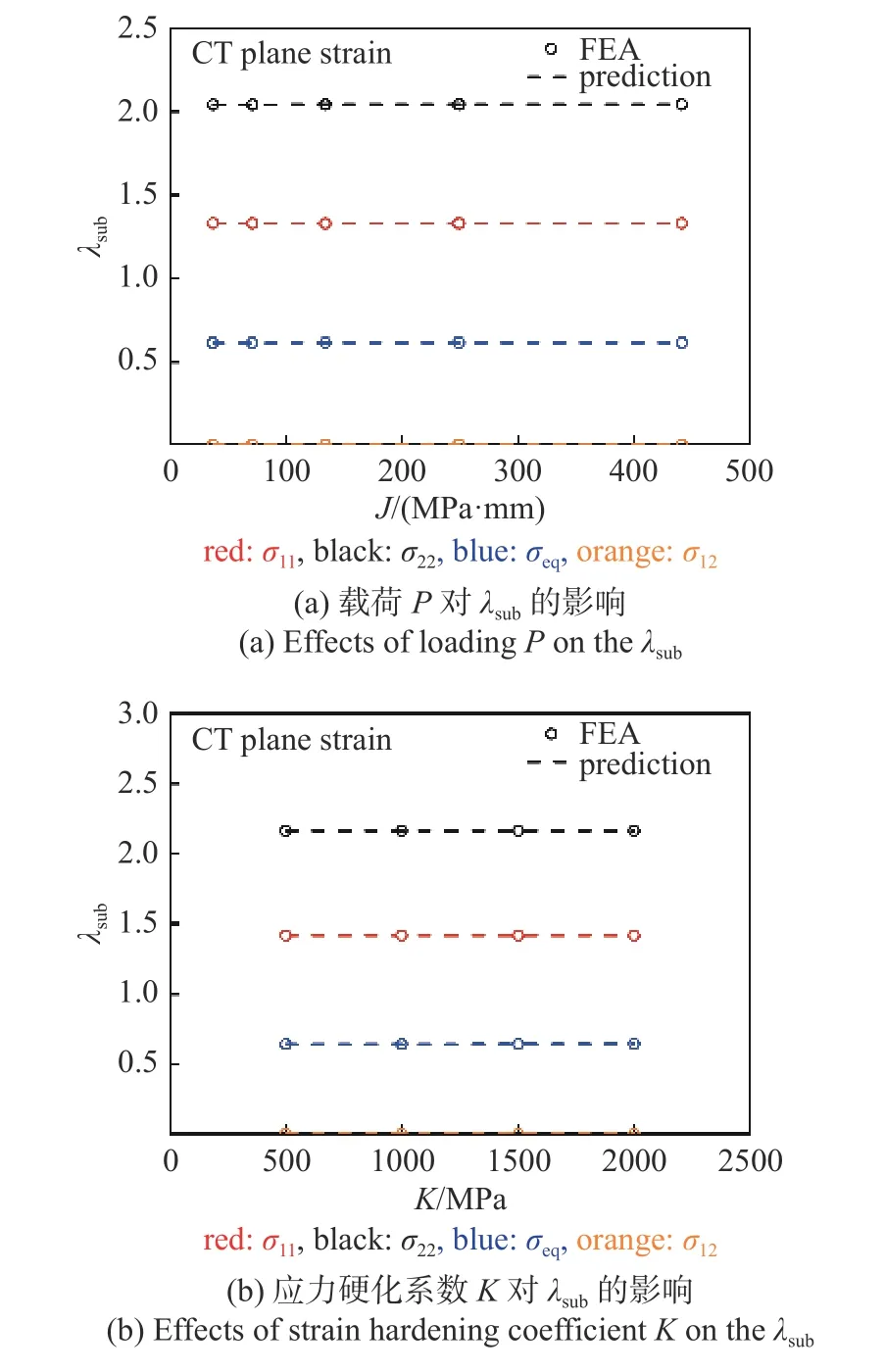
圖8 載荷P 和應(yīng)力硬化系數(shù)K 對λsub 的影響Fig.8 Effects of loading P and strain hardening coefficient K on the λsub

將無量綱裂紋長度a/W和應(yīng)變硬化系數(shù)K分別固定為0.6 和1000 MPa,以σM作為特征應(yīng)力,獲得無量綱應(yīng)力分布系數(shù)λsub如圖9 所示,在不同硬化指數(shù)下,λsub隨θ呈規(guī)律性變化;psub0與psub1均可以近似表示為與硬化指數(shù)N冪律相關(guān)的函數(shù),如圖10所示.類比三角特殊函數(shù)表征線彈性裂尖應(yīng)力場[31],式(18)整理可得不同應(yīng)力的λsub如下

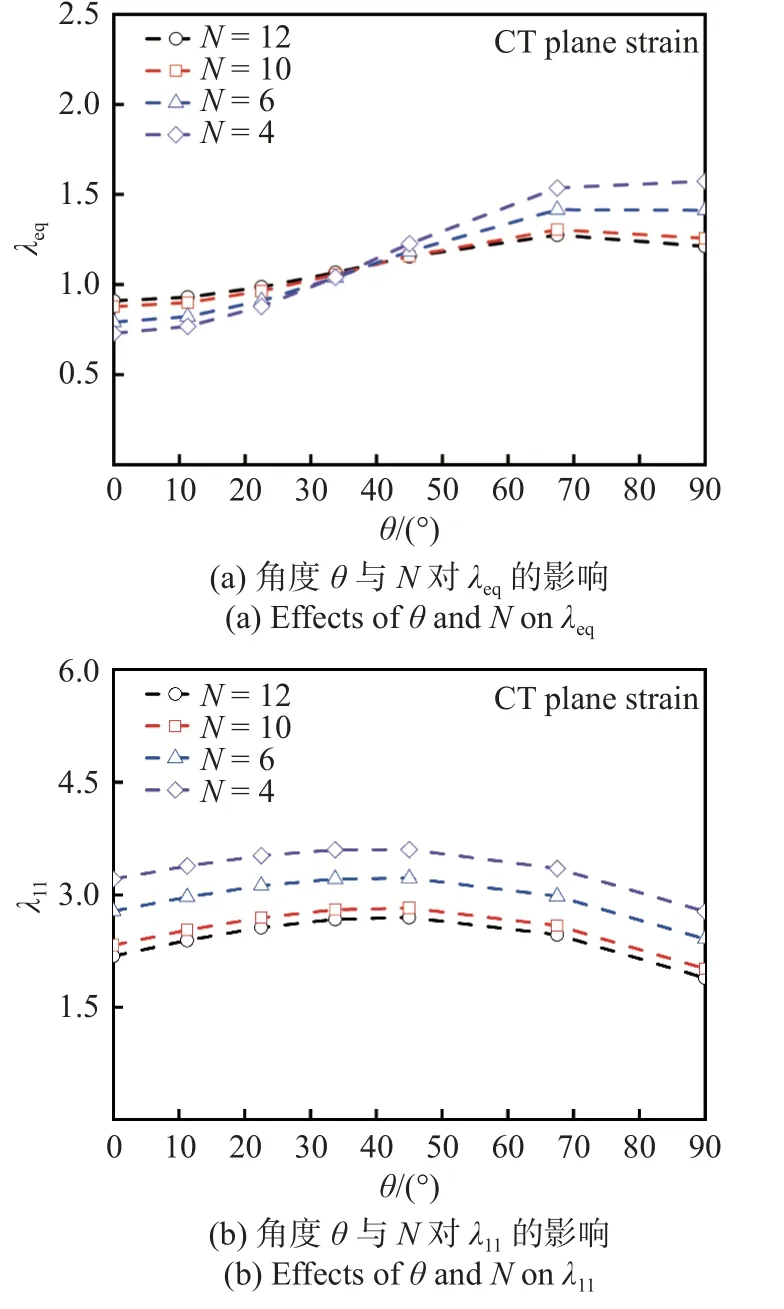
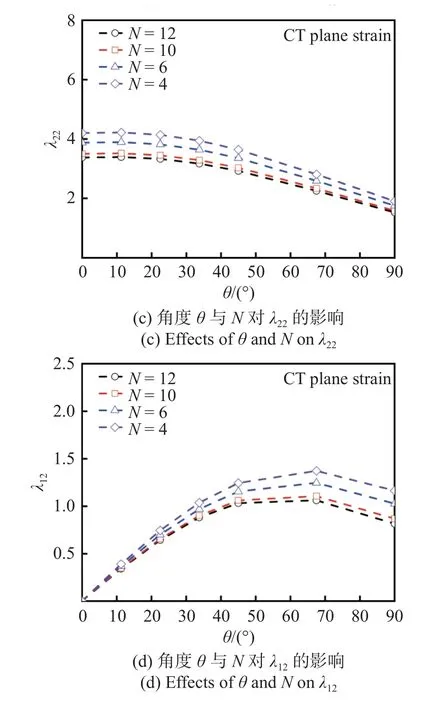
圖9 角度θ 與N 對λsub 的影響Fig.9 Effects of θ and N on λsub

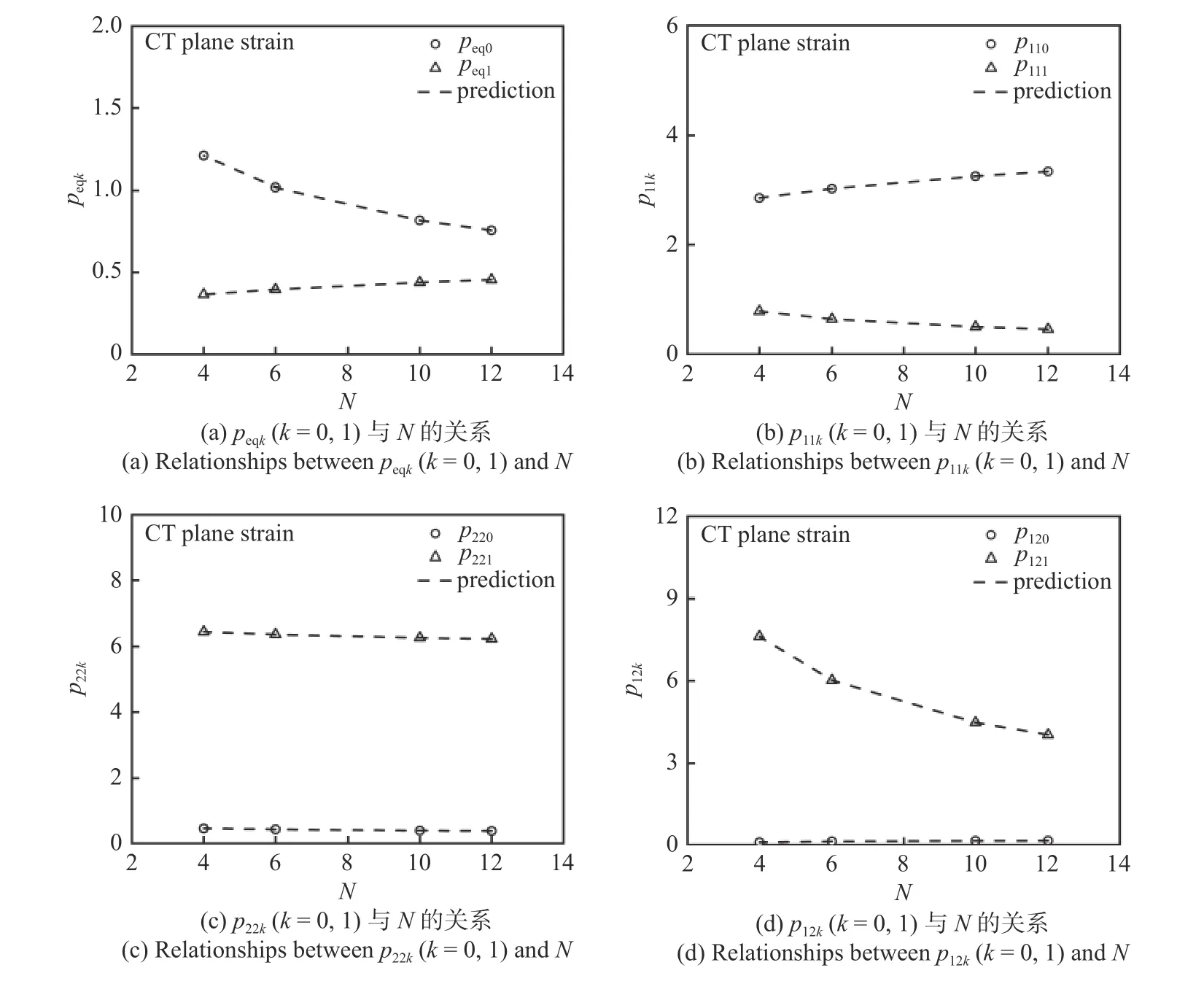
圖10 psubk(k=0,1)與N 的關(guān)系Fig.10 Relationships between psubk(k=0,1) and N

式中,psubk(k=0,1)與qsubm(m=0,1,2,3)為待定參數(shù),psubk(k=0,1)與N相關(guān),csubk(k=0,1),bsubk(k=0,1)為psubk(k=0,1)的待定參數(shù).

綜上,平面冪律塑性I 型裂紋尖端應(yīng)力場半解析模型可顯式表達(dá)為

式中,參數(shù)csubk,bsubk(k=0,1) 與參數(shù)qsubm(k=0,1,2,3)列于表4.

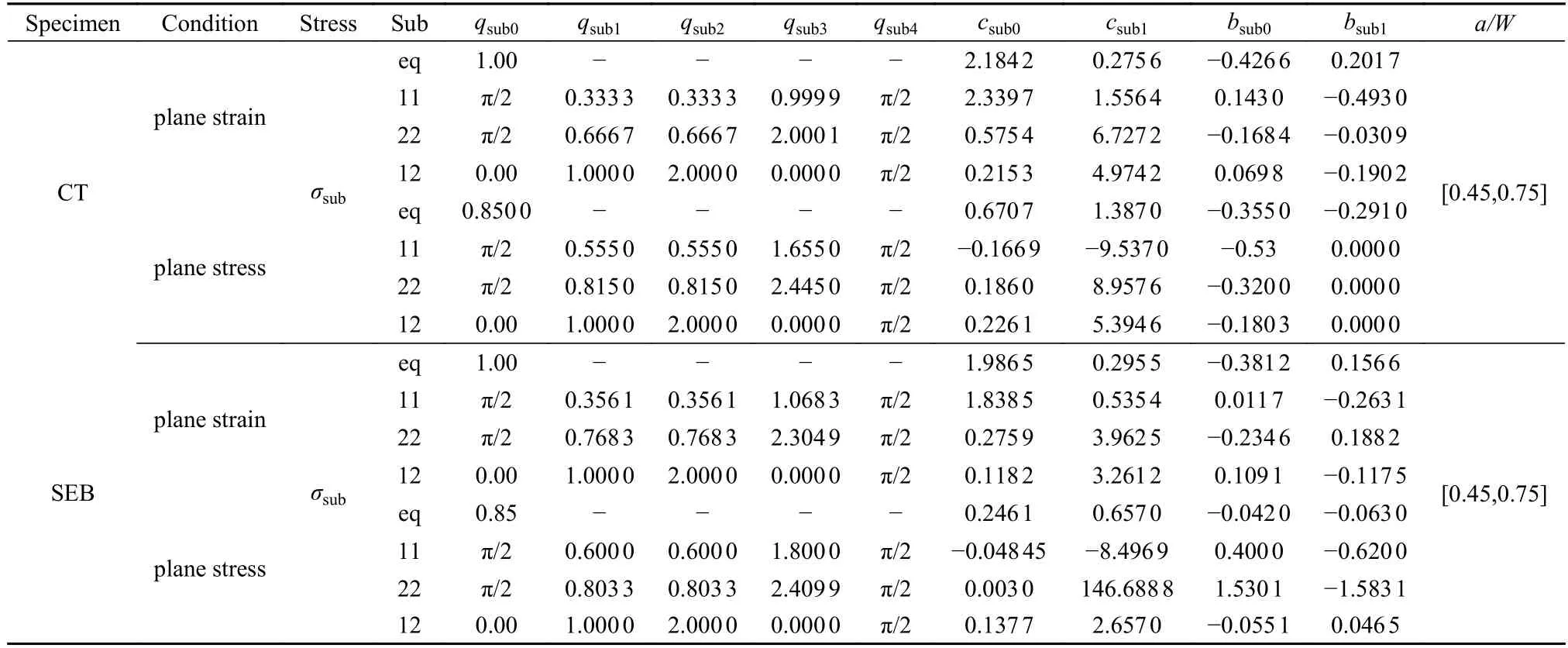
表4 模型參數(shù)Table 4 Parameters of model

3 模型驗(yàn)證

3.1 應(yīng)力分布的驗(yàn)證

圖8 表明應(yīng)力分布系數(shù)λsub與應(yīng)力硬化系數(shù)K無關(guān),而本文標(biāo)定參數(shù)選用硬化指數(shù)N=4,6,10,12,故本文模型材料參數(shù)使用范圍為N=4～ 12,表1～表4 給出了相應(yīng)的公式參數(shù)及其適用范圍,根據(jù)式(25)可預(yù)測CT 試樣和SEB 試樣的裂尖應(yīng)力分布.圖11～ 圖14 分別給出了CT 試樣和SEB 試樣在平面應(yīng)變、平面應(yīng)力條件下的不同裂紋長度和不同硬化指數(shù)下,FEA 和本文公式預(yù)測的徑向應(yīng)力分布對比;圖15～ 圖18 分別給出了CT 試樣和SEB 試樣在平面應(yīng)變、平面應(yīng)力條件下的不同裂紋長度和不同硬化指數(shù)下,裂紋尖端徑向距離不同情況下的FEA 和本文公式預(yù)測的環(huán)向應(yīng)力分布對比.結(jié)果表明本文模型預(yù)測的結(jié)果與FEA 結(jié)果均吻合良好.

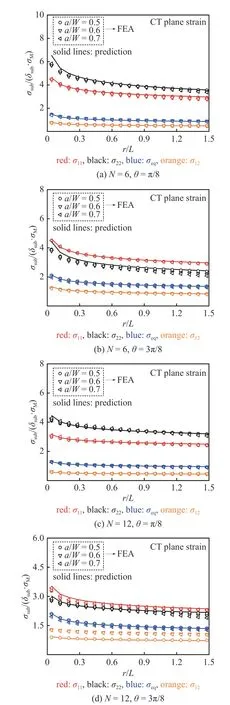
圖11 CT 試樣平面應(yīng)變條件下裂尖無量綱應(yīng)力徑向分布對比Fig.11 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of CT specimens under plane strain conditions

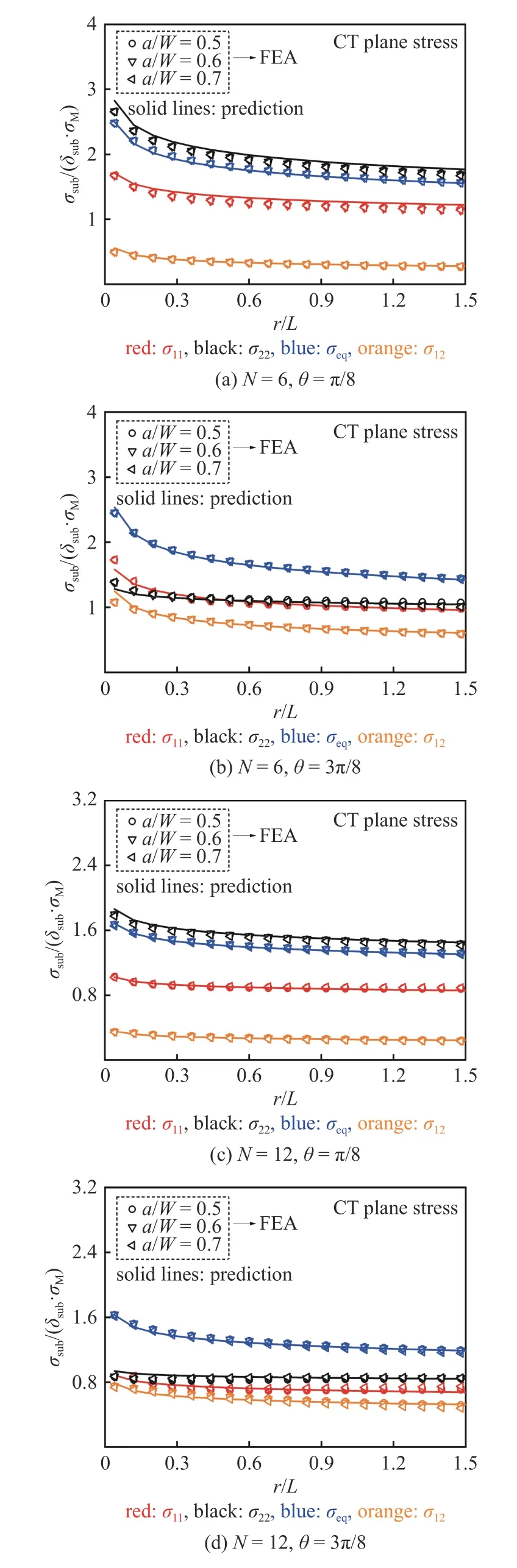
圖12 CT 試樣平面應(yīng)力條件下裂尖無量綱應(yīng)力徑向分布對比Fig.12 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of CT specimens under plane stress conditions

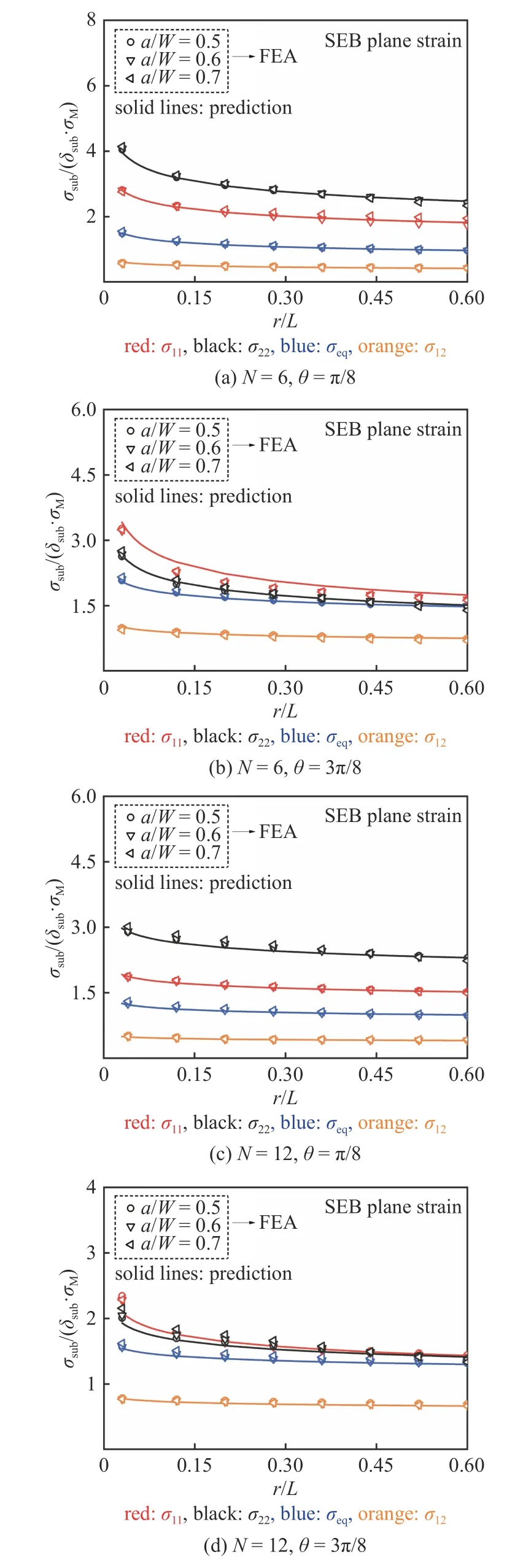
圖13 SEB 試樣平面應(yīng)變條件下裂尖無量綱應(yīng)力徑向分布對比Fig.13 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of SEB specimens under plane strain conditions

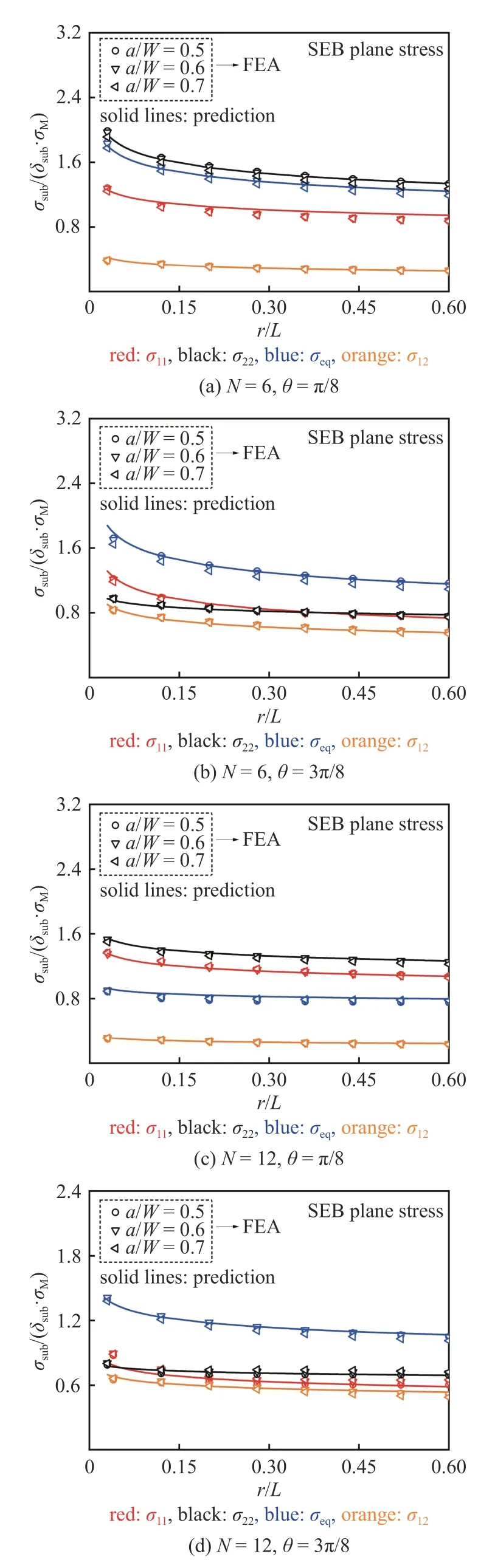
圖14 SEB 試樣平面應(yīng)力條件下裂尖無量綱應(yīng)力徑向分布對比Fig.14 Comparison with FEA and predicted results by Eq.(25) for normalized stress radial distributions near the crack tip of SEB specimens under plane stress conditions

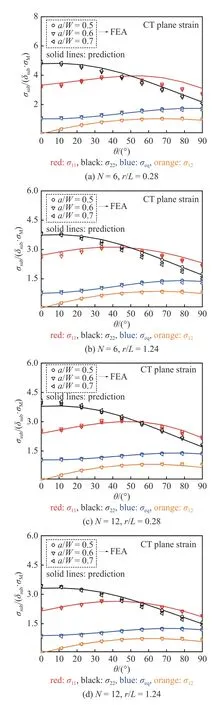
圖15 CT 試樣平面應(yīng)變條件下裂尖無量綱應(yīng)力環(huán)向分布對比Fig.15 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of CT specimens under plane strain conditions

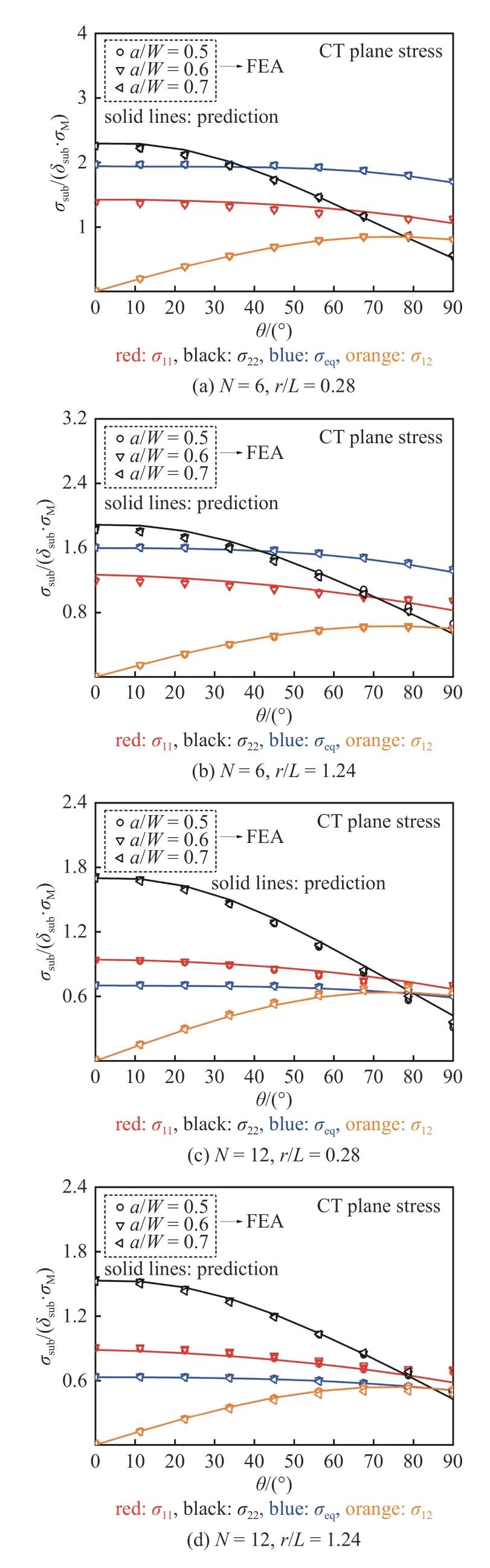
圖16 CT 試樣平面應(yīng)力條件下裂尖無量綱應(yīng)力環(huán)向分布對比Fig.16 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of CT specimens under plane stress conditions

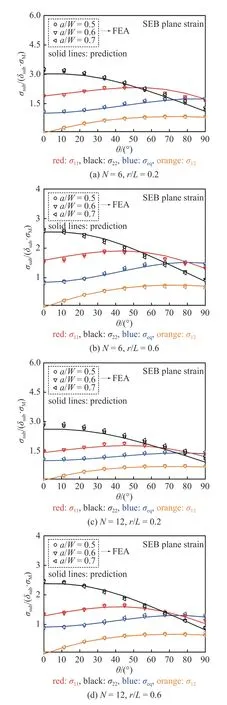
圖17 SEB 試樣平面應(yīng)變條件下裂尖無量綱應(yīng)力環(huán)向分布對比Fig.17 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of SEB specimens under plane strain conditions

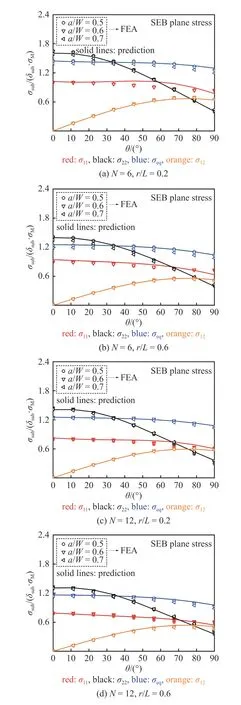
圖18 SEB 試樣平面應(yīng)力條件下裂尖無量綱應(yīng)力環(huán)向分布對比Fig.18 Comparison with FEA and predicted results by Eq.(25) for normalized stress angular distributions near the crack tip of SEB specimens under plane stress conditions

3.2 等效應(yīng)力等值線驗(yàn)證

根據(jù)式(25)可推導(dǎo)出平面I 型裂紋有限尺寸試樣等效應(yīng)力等值線表達(dá)式

考慮極限載荷PL表達(dá)式為[32]

圖19、圖20 和圖21、圖22 分別給出了CT試樣和SEB 試樣加載到極限載荷PL時(shí),不同裂紋長度和硬化指數(shù)下,有限元分析得到的等效應(yīng)力等值線與方程(26)預(yù)測的等效應(yīng)力等值線對比,當(dāng)?shù)刃?yīng)力σeq達(dá)到屈服應(yīng)力σ0時(shí),等效應(yīng)力等值線表示塑性區(qū)邊界.結(jié)果顯示,預(yù)測的結(jié)果與有限元分析結(jié)果吻合良好.

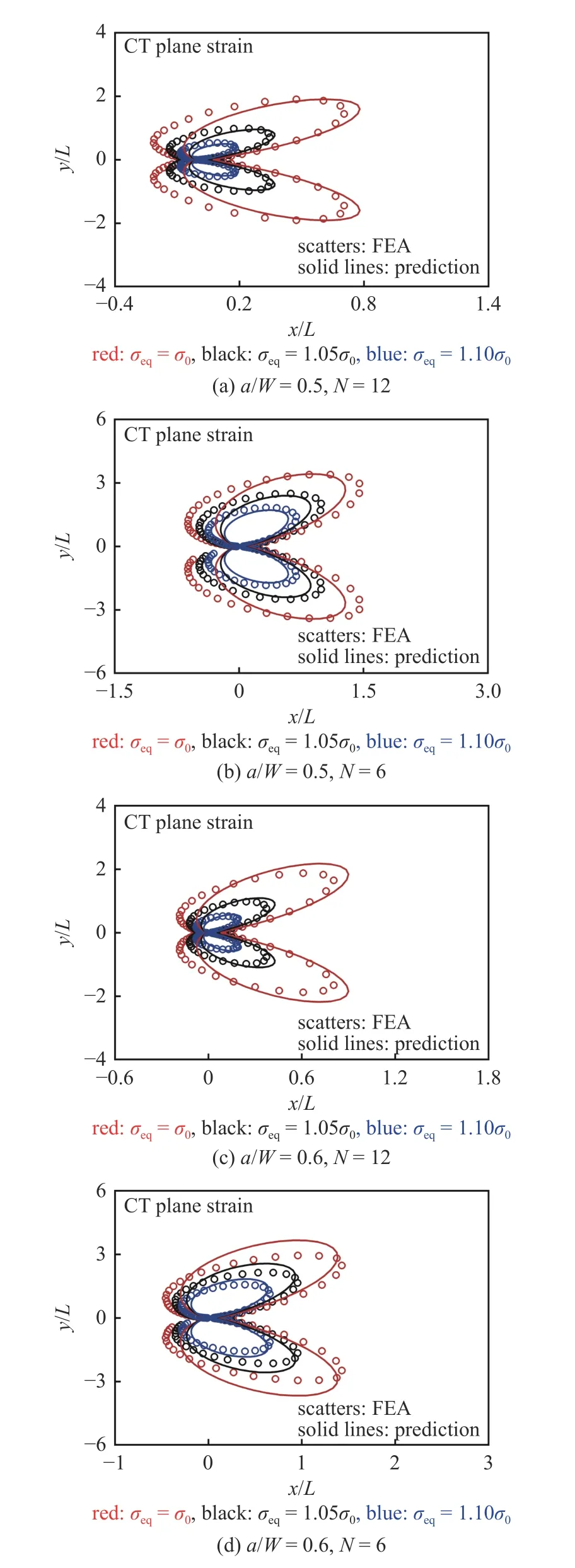
圖19 CT 試樣平面應(yīng)變條件下等效應(yīng)力σeq 等效應(yīng)力等值線對比Fig.19 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of CT specimen under plane strain conditions

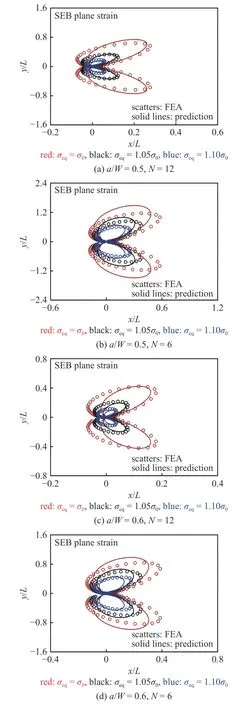
圖20 SEB 試樣平面應(yīng)變條件下等效應(yīng)力σeq 等效應(yīng)力等值線對比Fig.20 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of SEB specimen under plane strain conditions

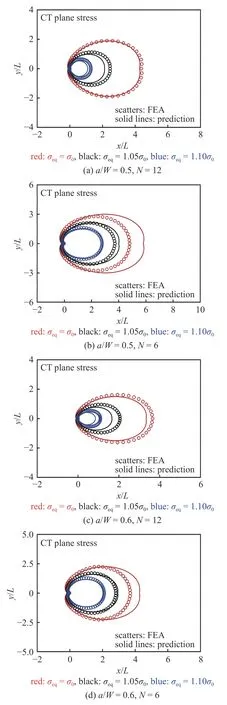
圖21 CT 試樣平面應(yīng)力條件下等效應(yīng)力σeq 等效應(yīng)力等值線對比Fig.21 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of CT specimen under plane stress conditions

圖22 SEB 試樣平面應(yīng)力條件下等效應(yīng)力σeq 等效應(yīng)力等值線對比Fig.22 Comparison with FEA results predicted by Eq.(26) for contour lines of the equivalent stress σeq near the crack tip of SEB specimen under plane stress conditions

4 結(jié)論

(1) 基于能量密度等效和量綱分析方法,推導(dǎo)了受單向加載構(gòu)元試樣中值能量密度RVE 的等效應(yīng)力解析方程,并定義其為σM應(yīng)力因子;

(2) 以應(yīng)力因子σM作為特征應(yīng)力,采用可用于裂尖等效應(yīng)力等值線表征的蝶翅輪廓式(平面應(yīng)變)和扇貝輪廓式(平面應(yīng)力)的三角特殊函數(shù),提出描述平面應(yīng)變和平面應(yīng)力冪律塑性I 型裂紋尖端應(yīng)力場的半解析模型;

(3) 針對平面應(yīng)變和平面應(yīng)力CT 和SEB 試樣,本文模型預(yù)測的應(yīng)力場與有限元分析結(jié)果均吻合良好.