含冷卻孔鎳基合金次級(jí)取向效應(yīng)的應(yīng)變梯度晶體塑性有限元研究1)

熊宇凱 趙建鋒 饒 威 黃志勇 康國政 張 旭,2)

* (西南交通大學(xué)力學(xué)與航空航天學(xué)院應(yīng)用力學(xué)與結(jié)構(gòu)安全四川省重點(diǎn)實(shí)驗(yàn)室,成都 610031)

? (中國工程物理研究院總體工程研究所,四川綿陽 621999)

** (北京工業(yè)大學(xué)材料與制造學(xué)部,北京 100124)

?? (四川大學(xué)空天科學(xué)與工程學(xué)院,成都 610065)

引言

單晶鎳基合金具有高強(qiáng)、高韌、抗疲勞等優(yōu)異性能,被廣泛用于航空發(fā)動(dòng)機(jī)渦輪葉片[1-5].為了降低葉片的服役溫度,通常在葉片上設(shè)計(jì)冷卻孔達(dá)到隔絕高溫燃?xì)獾哪康?然而,葉片在服役過程中冷卻孔附近易產(chǎn)生應(yīng)力集中,最終會(huì)降低葉片整體強(qiáng)度[6].另一方面,冷卻孔附近的應(yīng)力狀態(tài)極為復(fù)雜,這會(huì)使得存在顯著各向異性效應(yīng)的單晶葉片的力學(xué)響應(yīng)變得十分復(fù)雜.因此需要對(duì)含孔單晶鎳基合金葉片的變形進(jìn)行系統(tǒng)分析.

單晶葉片的制造工藝復(fù)雜,通過螺旋選晶法可以控制鎳基單晶主應(yīng)力軸的取向.主取向?yàn)閇001]的鎳基合金葉片具有優(yōu)異的綜合力學(xué)性能.但由于無法控制次級(jí)取向,[100]和[110]等次級(jí)取向會(huì)隨機(jī)形成[7-8].由于單晶具有較強(qiáng)的各向異性,次級(jí)取向?qū)η?qiáng)度有較大影響[9].研究發(fā)現(xiàn)當(dāng)單孔鎳基合金薄板的次級(jí)取向?yàn)閇100]時(shí),不易發(fā)生滑移面的剪切變形[10].另一個(gè)影響鎳基合金薄板力學(xué)性能的重要因素為冷卻孔.實(shí)驗(yàn)發(fā)現(xiàn)單孔薄板[110]強(qiáng)度高于[100],而含孔薄板[100]強(qiáng)度高于[110][11-12],表明冷卻孔是影響次級(jí)取向效應(yīng)的主要原因.同時(shí)冷卻孔數(shù)量也對(duì)力學(xué)性能具有重要影響,研究發(fā)現(xiàn)多孔之間存在強(qiáng)烈的干涉效應(yīng)[13],且冷卻孔數(shù)量的增加將降低蠕變壽命[14].

單晶鎳基合金具有多個(gè)滑移系,滑移系的開動(dòng)情況對(duì)含冷卻孔薄板的強(qiáng)度具有重要影響[15-16].已有研究表明晶體塑性有限元可在滑移系層次有效分析含孔薄板的塑性變形行為[6,17-23].在晶體塑性本構(gòu)模型中引入損傷參數(shù)可用于解釋裂紋擴(kuò)展模式受次級(jí)取向的影響機(jī)制[24].晶體塑性有限元方法可以預(yù)測(cè)單個(gè)冷卻孔附近的應(yīng)力狀態(tài)以及裂紋萌生位置[25].除了單拉變形外,多機(jī)制晶體塑性本構(gòu)還可預(yù)測(cè)復(fù)雜加載工況下的變形行為(應(yīng)變控制循環(huán)以及蠕變等[26-27]).上述研究表明晶體塑性有限元方法可以準(zhǔn)確描述含冷卻孔鎳基單晶薄板的各向異性力學(xué)行為,但大多數(shù)研究主要關(guān)注單孔的作用.在與工程實(shí)際相符的多孔薄板研究方面,晶體塑性模擬發(fā)現(xiàn)孔之間的相互作用將影響孔附近的應(yīng)力狀態(tài)以及位錯(cuò)密度分布[28].通過有限元模擬還可以解釋原位實(shí)驗(yàn)中多孔附近出現(xiàn)的X 型塑性應(yīng)變區(qū)[29].實(shí)驗(yàn)發(fā)現(xiàn)薄板取向?yàn)閇100]的多孔的分布將影響斷口形貌,卻不影響塑性滑移帶方向,塑性滑移帶與加載軸始終成45°[30-31],表明滑移帶分布不是由冷卻孔排列方式主導(dǎo),而受加載取向的影響更大.但當(dāng)前研究還未闡明冷卻孔間滑移帶區(qū)域的變形特征以及次級(jí)取向效應(yīng).此外,冷卻孔周圍存在塑性應(yīng)變梯度,需要幾何必需位錯(cuò)密度協(xié)調(diào)[32].然而目前晶體塑性研究大多未考慮應(yīng)變梯度效應(yīng).所以有必要采用非局部晶體塑性本構(gòu)模型[33,34]分析多孔的次級(jí)取向效應(yīng)以及冷卻孔引起的應(yīng)變梯度效應(yīng).

本文將重點(diǎn)探究次級(jí)取向效應(yīng)對(duì)單孔和多孔鎳基合金薄板塑性變形的影響,分析塑性變形階段滑移系上塑性滑移和微結(jié)構(gòu)的演化,從而揭示次級(jí)取向?qū)е聫?qiáng)度變化的內(nèi)在本質(zhì)并闡明了冷卻孔引起的非均勻變形特征.

1 非局部晶體塑性模型

本文所采用的本構(gòu)模型為非局部晶體塑性模型[35],此模型基于位錯(cuò)機(jī)制,通過塑性變形梯度與幾何必需位錯(cuò)密度的關(guān)系導(dǎo)出位錯(cuò)流動(dòng)項(xiàng),使其成為非局部模型[36].模型考慮了金屬材料內(nèi)部位錯(cuò)的多種行為,已有研究表明此模型可以很好描述鋁的雙晶壓縮以及單晶鎳的壓痕變形行為[37],因此可以使用此模型描述同樣含有多種位錯(cuò)行為的鎳基合金的塑性變形.

1.1 運(yùn)動(dòng)學(xué)與位錯(cuò)增殖

將材料點(diǎn)總的變形梯度F可以分解為晶格彈性變形和剛體轉(zhuǎn)動(dòng)引起的彈性變形梯度Fe以及位錯(cuò)滑移導(dǎo)致的塑性變形梯度Fp兩部分

塑性變形梯度的演化率可表示為

其中位錯(cuò)沿滑移面運(yùn)動(dòng)導(dǎo)致的塑性速度梯度Lp可以通過塑性滑移率描述

其中sα為滑移方向單位矢量,nα為滑移面法向單位矢量,Nslip為滑移系數(shù)量,鎳基合金為面心立方(FCC)材料,具有12 個(gè)滑移系.

位錯(cuò)在本模型中根據(jù)位錯(cuò)類型被分為可動(dòng)位錯(cuò)、不可動(dòng)位錯(cuò)以及位錯(cuò)偶3 類,其中可動(dòng)位錯(cuò)與不可動(dòng)位錯(cuò)根據(jù)正負(fù)性又進(jìn)一步細(xì)分為正刃型、負(fù)刃型、正螺型和負(fù)螺型4 種.塑性滑移率使用Orowan 方程[38]描述,通過可動(dòng)位錯(cuò)的運(yùn)動(dòng)描述材料產(chǎn)生的塑性滑移,α滑移系上塑性滑移率為

位錯(cuò)密度演化包含3 個(gè)部分,分別為位錯(cuò)增殖、位錯(cuò)湮滅以及位錯(cuò)偶與單位錯(cuò)的轉(zhuǎn)變.為表示位錯(cuò)增值率,基于位錯(cuò)環(huán)[39]構(gòu)型,假定不同類型位錯(cuò)的增殖率[36]相同,則位錯(cuò)增值率可表示為

1.2 位錯(cuò)類型轉(zhuǎn)變

位錯(cuò)偶是由單個(gè)正位錯(cuò)與單個(gè)負(fù)位錯(cuò)組成,當(dāng)自由運(yùn)動(dòng)的兩個(gè)異號(hào)位錯(cuò)的滑移面間距小于一臨界值時(shí),異號(hào)位錯(cuò)之間的交互作用力可與外加分切應(yīng)力平衡,異號(hào)位錯(cuò)形成穩(wěn)定的位錯(cuò)偶構(gòu)型.刃型位錯(cuò)偶演化率與螺型位錯(cuò)偶演化率分別為

1.3 位錯(cuò)湮滅

位錯(cuò)偶的湮滅類型有2 種,分別為熱激活和無熱激活的湮滅.刃型位錯(cuò)發(fā)生面外運(yùn)動(dòng)即攀移過程需要熱激活,則攀移造成的刃型位錯(cuò)偶的演化率為

其中Ω為原子體積,為自擴(kuò)散系數(shù),ΔHSD為自擴(kuò)散激活熵,kB為玻爾茲曼常數(shù),T為溫度.

當(dāng)位錯(cuò)偶中兩個(gè)單位錯(cuò)的距離小于穩(wěn)定存在的下界時(shí),刃型和螺型位錯(cuò)偶均可發(fā)生湮滅,無需熱激活即可湮滅導(dǎo)致刃型位錯(cuò)偶演化率與螺型位錯(cuò)偶演化率分別為

由于螺型位錯(cuò)偶的湮滅方式為交滑移,此過程將留下刃型割階.螺位錯(cuò)交滑移對(duì)正、負(fù)刃型位錯(cuò)密度演化率的貢獻(xiàn)為

其中k3為比例因子.

1.4 位錯(cuò)運(yùn)動(dòng)速度

位錯(cuò)運(yùn)動(dòng)速度受固溶障礙、Peierls 障礙以及黏滯作用3 個(gè)因素影響,則位錯(cuò)速度vα可表達(dá)為

其中cat為原子濃度,黏滯速度vT可表示為η為黏滯系數(shù),tS和tP分別為位錯(cuò)在固溶原子和Peierls障礙前的滯留時(shí)間,其停滯時(shí)間與位錯(cuò)嘗試穿越障礙的頻率和位錯(cuò)成功跨越障礙的概率相關(guān)

其中,f為位錯(cuò)嘗試越過障礙的頻率,τ為障礙強(qiáng)度,dobst為固溶原子直徑,wk為位錯(cuò)雙扭折寬度,p,q為障礙激活能輪廓系數(shù).

位錯(cuò)在滑移面運(yùn)動(dòng)受林位錯(cuò)的阻礙,則滑移面有效分切應(yīng)力[41]τeff可以表示為α滑移系上驅(qū)動(dòng)力τα減去位錯(cuò)阻力

其中位錯(cuò)之間相互作用力 τcr可以表示為

其中G為剪切模量,為滑移系之間位錯(cuò)相互作用強(qiáng)度系數(shù).

1.5 位錯(cuò)流動(dòng)

通過Nye 張量 αα建立塑性畸變張量 βα與位錯(cuò)密度的關(guān)系[42]

式中,lα表示α滑移系上沿著位錯(cuò)線方向的單位向量,由于正、負(fù)位錯(cuò)在求和過程中抵消,所以只有幾何必需位錯(cuò)協(xié)調(diào)非均勻變形.

定義滑移系上位錯(cuò)流量為可動(dòng)位錯(cuò)密度與其運(yùn)動(dòng)速度的乘積fα=ραvα,則上式可寫為

本模型通過設(shè)置位錯(cuò)在表面的穿透因子χ控制位錯(cuò)在模型表面的流動(dòng).采用有限體積離散方法,位錯(cuò)流入鄰近單元可表示為

其中V是體元體積,An是編號(hào)n的面元面積,an是面法向矢量.

2 晶體塑性模型有限元實(shí)現(xiàn)

2.1 有限元模型及邊界條件

單孔和多孔鎳基合金板有限元模型(圖1)尺寸參照實(shí)驗(yàn)[25,29]中的試樣尺寸和孔分布.單孔和多孔的單元數(shù)量分別為9580 和29125,單元類型均為C3D8R.模型約束x-y面的x和y方向位移,在x-y面沿z軸應(yīng)變控制加載,應(yīng)變率為 1 ×10?4s?1,其余面均無約束.

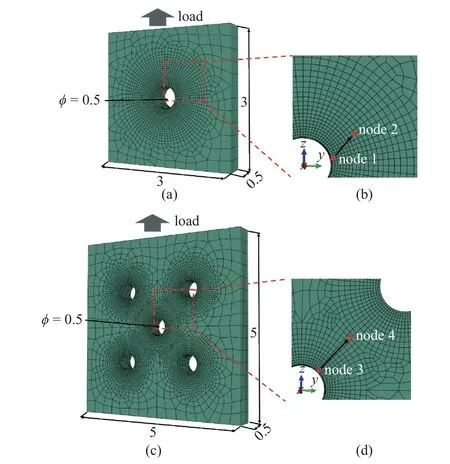
圖1 鎳基合金薄板有限元模型示意圖: (a),(b)單孔薄板;(c),(d)多孔薄板 (單位: mm)Fig.1 Finite element model of Ni-based alloy plate: (a),(b) plate with a hole;(c),(d) plate with five holes

本文模擬含孔鎳基合金薄板兩種次級(jí)取向的單拉響應(yīng),由于鎳基合金的常用制備工藝只能控制平行于渦輪葉片平面的主級(jí)取向[001],實(shí)驗(yàn)與模擬中也將[001]方向作為加載方向[32].因此,本文的兩種薄板也沿主級(jí)取向([001]方向)拉伸,采用的次級(jí)取向(沿板厚方向)為常用于實(shí)驗(yàn)和模擬研究的[100]取向和[110]取向[15,19,34,43-45],如圖2 所示.

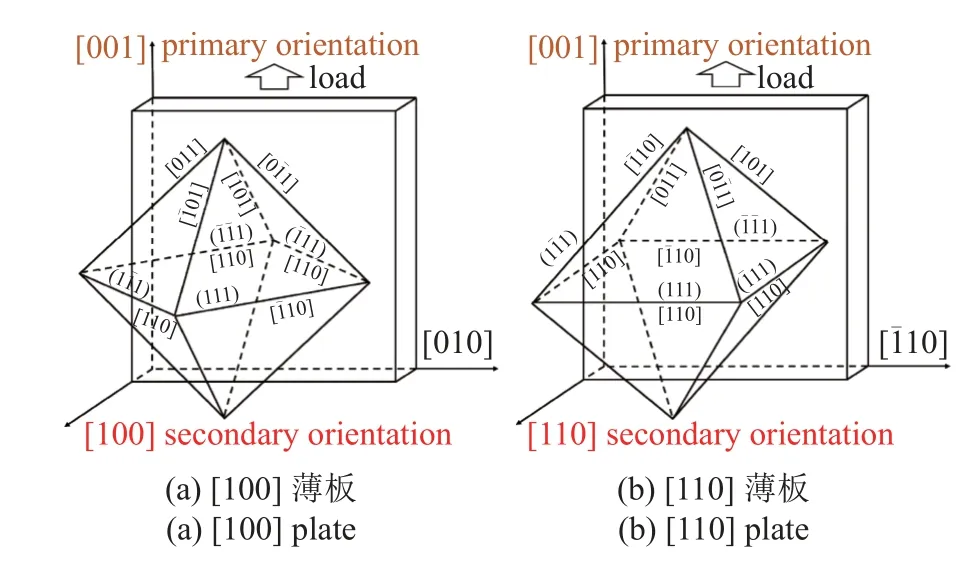
圖2 鎳基合金薄板次級(jí)取向示意圖Fig.2 Secondary orientation of Ni-based alloy plate

2.2 本構(gòu)模型參數(shù)驗(yàn)證

FCC 的12 個(gè)滑移系之間共有6 種交互作用類型[46],相互作用強(qiáng)度系數(shù)取值分別為: 自硬化0.122、共面作用0.122、共線作用0.625、Hirth 鎖0.07、可動(dòng)割階0.137 以及Lomer 鎖0.122.

通過實(shí)驗(yàn)[29]得到的鎳基合金無孔薄板單軸拉伸應(yīng)力?應(yīng)變曲線校準(zhǔn)本構(gòu)模型參數(shù).鎳基合金的表面穿透系數(shù)χ取1,其余本構(gòu)模型參數(shù)見表1.如圖3所示,[100] 單孔薄板與無孔薄板的單拉應(yīng)力?應(yīng)變曲線模擬結(jié)果與實(shí)驗(yàn)可以較好吻合.且驗(yàn)證了當(dāng)前網(wǎng)格密度滿足精確性要求,如圖4 所示.

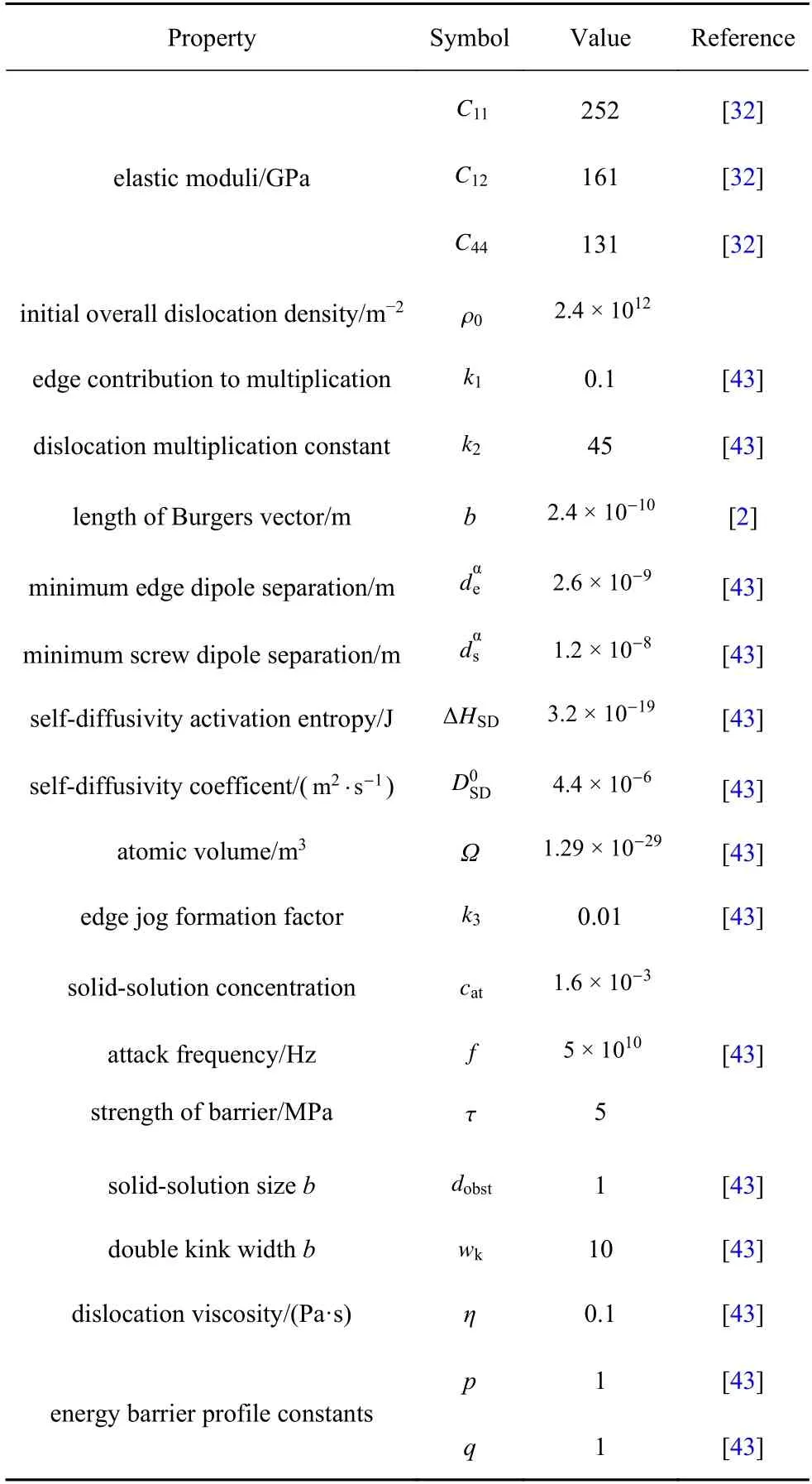
表1 鎳基合金的非局部晶體塑性模型參數(shù)Table 1 Model parameters for nonlocal crystal plasticity used for Ni-based alloys

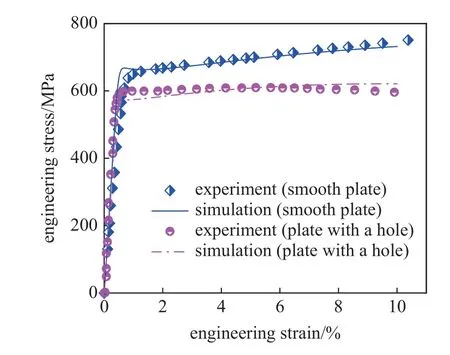
圖3 無孔和單孔[100]鎳基合金薄板模擬和實(shí)驗(yàn)結(jié)果[29]對(duì)比Fig.3 Comparison of simulation and experimental results[29] for [100]plate without hole and with a hole,respectively

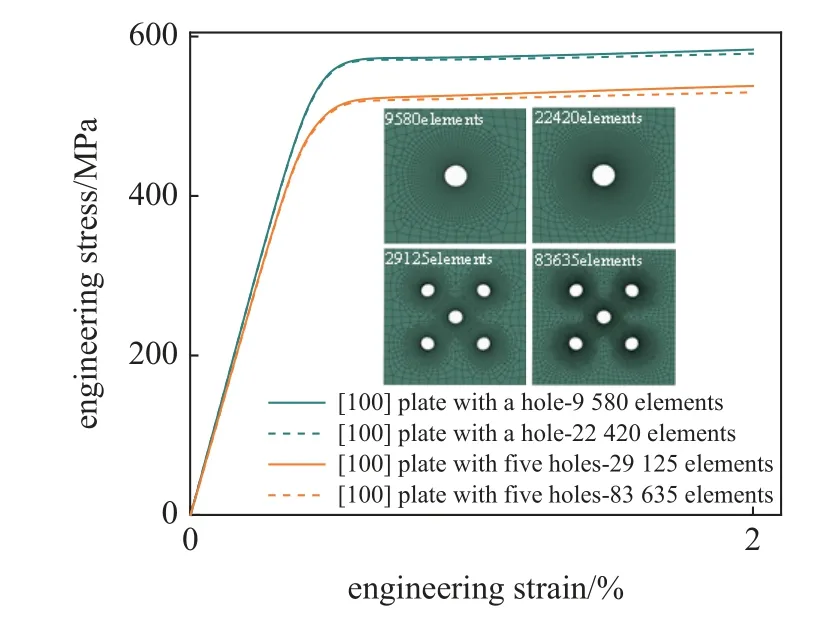
圖4 不同單元數(shù)目單孔和多孔薄板單軸拉伸模擬結(jié)果Fig.4 Uniaxial tensile simulation results of one-hole plates and fivehole plates with different element numbers

3 結(jié)果與討論

3.1 單軸拉伸響應(yīng)

圖5 為兩種次級(jí)取向的單孔和多孔鎳基合金薄板單軸拉伸應(yīng)力?應(yīng)變響應(yīng)曲線.模擬結(jié)果表明含冷卻孔薄板具有較強(qiáng)的次級(jí)取向效應(yīng),[100]薄板強(qiáng)度均高于[110]薄板強(qiáng)度,且多孔薄板的次級(jí)取向效應(yīng)比單孔更強(qiáng).

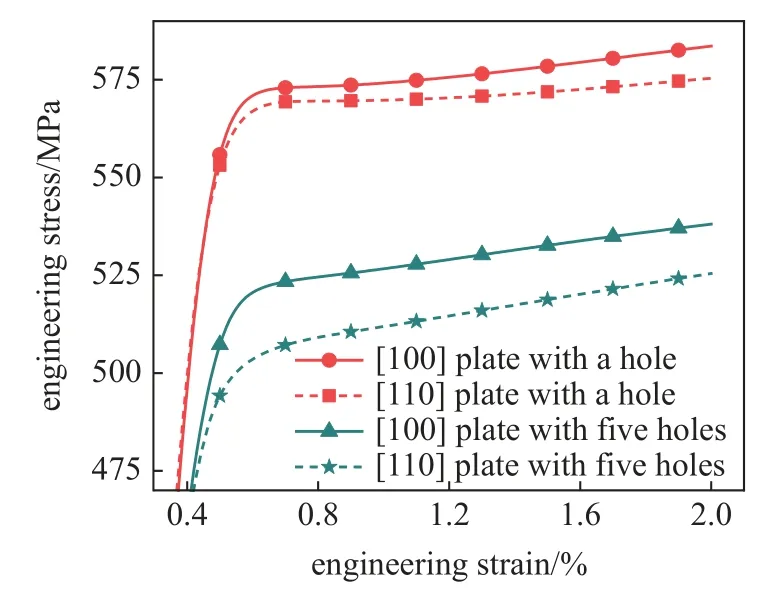
圖5 兩種次級(jí)取向的單孔和多孔薄板單軸拉伸模擬結(jié)果Fig.5 Uniaxial tensile simulation results of one-hole plates and fivehole plates in two secondary orientations

3.2 塑性滑移

總塑性滑移量反映了塑性變形區(qū),可通過單滑移系的塑性滑移計(jì)算得到

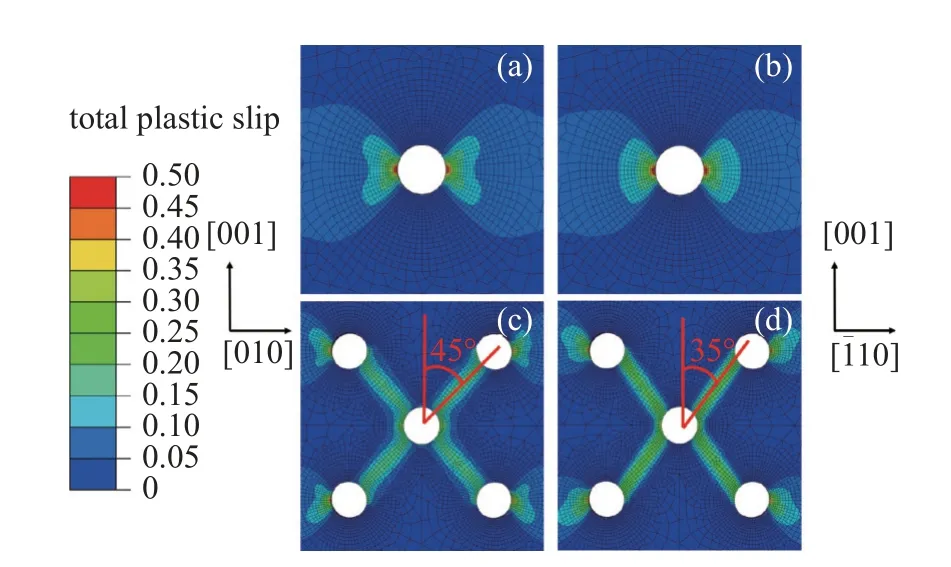
圖6 應(yīng)變?yōu)?%時(shí)總塑性滑移分布: (a),(c) [100];(b),(d) [110]Fig.6 Total plastic slip at 2% strain: (a),(c) [100];(b),(d) [110]

圖7 [100]取向薄板表面塑性滑移帶[30]Fig.7 Plastic slip bands on the surface of [100] plate[30]

圖8 為拉伸應(yīng)變?yōu)?% 時(shí)滑移系開動(dòng)的數(shù)量,當(dāng)單滑移系塑性滑移大于0.01 時(shí)視為此滑移系開動(dòng).在孔洞附近不僅存在最大塑性滑移,且開動(dòng)的滑移系數(shù)量最多達(dá)到8 個(gè),表明此處為薄板最薄弱處,實(shí)驗(yàn)結(jié)果也表明裂紋最先從孔兩側(cè)位置萌生[45].對(duì)于[100]取向的兩種薄板,在塑性滑移核心區(qū)開動(dòng)的滑移系數(shù)量均達(dá)到6 個(gè),而[110]取向的兩種薄板只有4 個(gè)滑移系開動(dòng).兩個(gè)取向薄板在塑性滑移量上雖然差別不大,但是滑移系開動(dòng)數(shù)量有明顯區(qū)別,前者具有更多滑移系協(xié)調(diào)塑性變形.

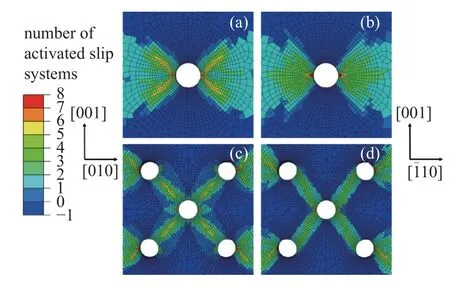
圖8 應(yīng)變?yōu)?%時(shí)滑移系開動(dòng)數(shù)量: (a),(c) [100];(b),(d) [110]Fig.8 The number of activated slip system at 2% strain: (a),(c) [100];(b),(d) [110]

為進(jìn)一步探究多孔分布位置對(duì)塑性滑移帶的影響,對(duì)比了不同冷卻孔分布位置以及冷卻孔數(shù)量[100]多孔薄板的總塑性滑移量,如圖9 所示.可以發(fā)現(xiàn)4 孔薄板和30°分布的5 孔薄板并未發(fā)生明顯的X 型滑移帶,這是由于冷卻孔之間沿拉伸方向的距離相對(duì)較遠(yuǎn);而45°分布的5 孔薄板和60°分布的5 孔薄板出現(xiàn)了明顯的X 型滑移帶,且滑移帶與加載方向約為45°.

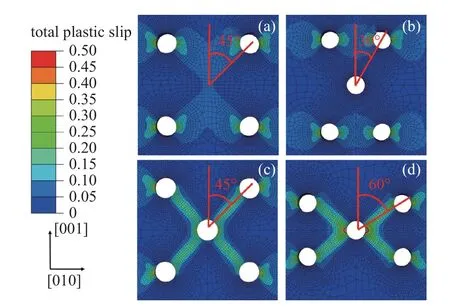
圖9 應(yīng)變?yōu)?%時(shí)不同冷卻孔分布的總塑性滑移: (a) 45°分布含4 孔,(b)30°分布含5 孔,(c) 45°分布含5 孔,(d) 60°分布含5 孔Fig.9 Total plastic slip at 2% strain with different cooling hole distribution: plate with (a) four-hole of 45° distribution,(b) five-hole of 30° distribution,(c) five-hole of 45° distribution,(d) five-hole of 60°distribution

3.3 分切應(yīng)力

由于塑性變形是由分切剪應(yīng)力驅(qū)動(dòng)滑移面上位錯(cuò)滑移運(yùn)動(dòng)所產(chǎn)生,本節(jié)通過分析孔附近分切剪應(yīng)力演化探究次級(jí)取向?qū)?yīng)力狀態(tài)的影響.其12 個(gè)滑移系編號(hào)對(duì)應(yīng)的滑移面和滑移方向如表2 所示.根據(jù)加載方向與滑移方向的關(guān)系,兩個(gè)次級(jí)取向均有8 個(gè)易開 動(dòng)滑移 系(ξ1,ξ2,ξ4,ξ5,ξ7,ξ8,ξ10,ξ11),沿[001]方向加載時(shí)其Schmid 因子均為0.408;以及4 個(gè)不易開動(dòng)滑移系(ξ3,ξ6,ξ9,ξ12),沿[001]方向加載時(shí)其Schmid 因子均為0.

表2 鎳基合金沿[001]加載時(shí)各滑移系Schmid 因子Table 2 Schmid factor of the Ni-based alloys loaded along[001] direction

在單孔和多孔模型均選取塑性變形帶方向上兩個(gè)節(jié)點(diǎn)(如圖1(b)中的節(jié)點(diǎn)1 和2 及圖1(d)中的節(jié)點(diǎn)3 和4)進(jìn)行分析.如圖10 所示,在距離孔較近位置(節(jié)點(diǎn)1),應(yīng)力狀態(tài)復(fù)雜為多軸應(yīng)力狀態(tài)[32],導(dǎo)致拉伸過程中滑移系分切應(yīng)力波動(dòng)較大且具有較大分散性.距離孔較遠(yuǎn)位置(節(jié)點(diǎn)2)處應(yīng)力狀態(tài)相對(duì)簡(jiǎn)單趨于單軸應(yīng)力狀態(tài),分切應(yīng)力較為穩(wěn)定且分散性較小.且多孔的分切應(yīng)力分散性整體大于單孔,離多孔較近位置(節(jié)點(diǎn)3) 的滑移系分切應(yīng)力波動(dòng)最劇烈.

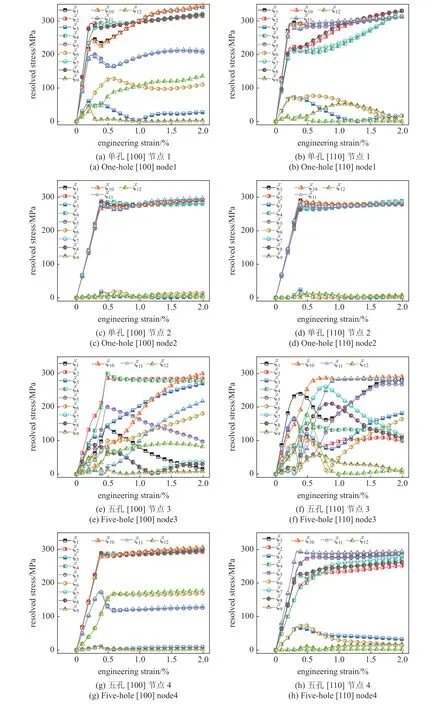
圖10 冷卻孔單側(cè)節(jié)點(diǎn)不同變形階段分切應(yīng)力的演化Fig.10 Evolution of resolved stress at one side nodes of cooling hole

圖11 顯示了應(yīng)變?yōu)?%時(shí)12 個(gè)滑移系中最大分切應(yīng)力的分布圖.在單孔和多孔板中,最大分切應(yīng)力均位于塑性滑移區(qū),且次級(jí)取向和孔數(shù)量對(duì)最大分切應(yīng)力影響不大.

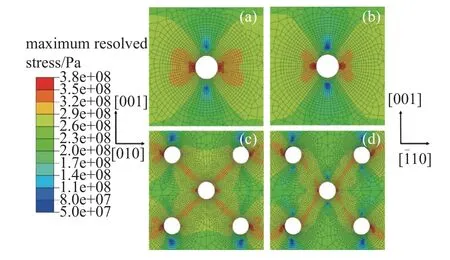
圖11 應(yīng)變?yōu)?%時(shí)最大分切應(yīng)力云圖: (a),(c) [100];(b),(d) [110]Fig.11 Maximum resolved stress at 2% strain: (a),(c) [100];(b),(d) [110]

3.4 主導(dǎo)滑移系

本節(jié)將分析塑性變形帶方向上兩個(gè)節(jié)點(diǎn)的主導(dǎo)滑移系塑性滑移演化規(guī)律及其對(duì)強(qiáng)韌性的影響.圖12 為12 個(gè)滑移系的塑性滑移量隨應(yīng)變的演化.可以發(fā)現(xiàn)取向和節(jié)點(diǎn)位置對(duì)塑性演化均有很大影響,不同節(jié)點(diǎn)處[100]取向薄板中滑移系的開動(dòng)數(shù)量均不低于[110]取向薄板,由此表明在整個(gè)變形過程中[100]取向薄板有更多的滑移系協(xié)調(diào)塑性變形.距離孔位置近的節(jié)點(diǎn)分切應(yīng)力波動(dòng)較大且滑移系開動(dòng)數(shù)量少,而遠(yuǎn)離孔邊緣的節(jié)點(diǎn)分切應(yīng)力趨于穩(wěn)定且滑移系開動(dòng)數(shù)量增多,表明穩(wěn)定的分切應(yīng)力更利于易開動(dòng)的8 個(gè)滑移系均勻開動(dòng).

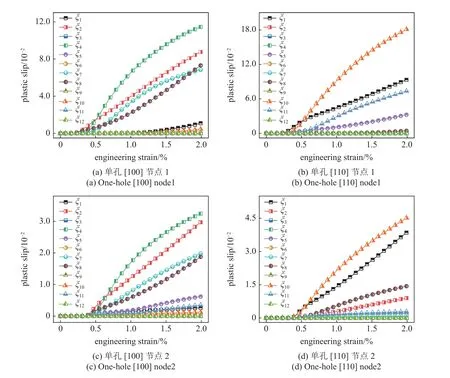
圖12 冷卻孔單側(cè)節(jié)點(diǎn)不同變形階段塑性滑移的演化Fig.12 Evolution of plastic slip at one side nodes of cooling hole

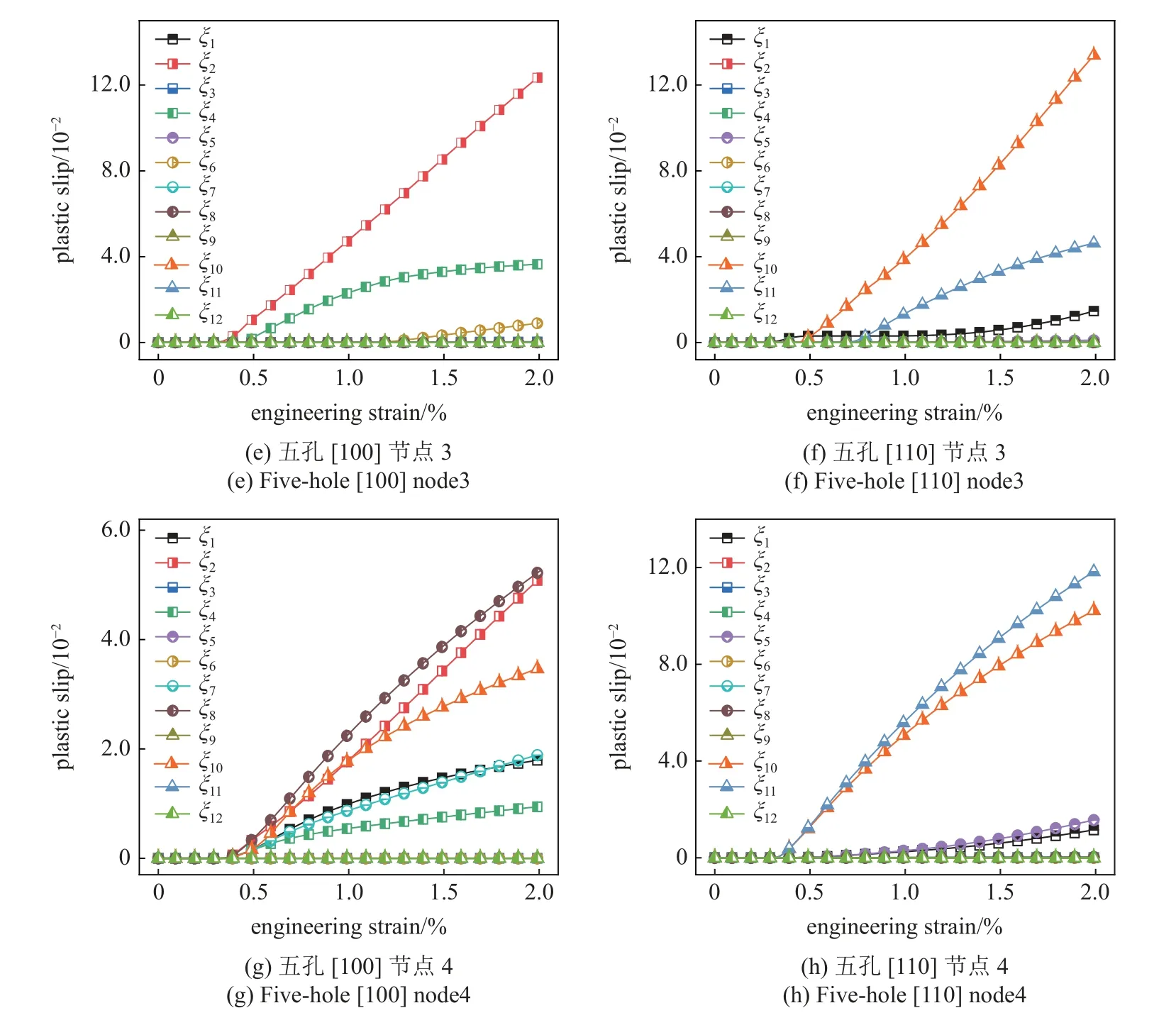
圖12 冷卻孔單側(cè)節(jié)點(diǎn)不同變形階段塑性滑移的演化(續(xù))Fig.12 Evolution of plastic slip at one side nodes of cooling hole (continued)

前文闡明了特定節(jié)點(diǎn)位置的滑移系開動(dòng)情況,后續(xù)將分析整體區(qū)域的主導(dǎo)滑移系(塑性滑移最大的滑移系).圖13 為應(yīng)變2%時(shí)主導(dǎo)滑移系分布,當(dāng)所有滑移系塑性滑移均小于0.01 時(shí),顯示為0.可以發(fā)現(xiàn)取向和孔數(shù)量不僅影響塑性滑移區(qū),還影響主導(dǎo)滑移系.單孔[100]取向薄板右上方區(qū)域的塑性滑移主要以 ξ4和ξ11兩個(gè)滑移系為主;[110]取向薄板右上方區(qū)域的塑性滑移主要以 ξ2和ξ10兩個(gè)滑移系為主.單孔兩種取向鎳基合金板的滑移系分布區(qū)域以及開動(dòng)情況與實(shí)驗(yàn)所觀察到的現(xiàn)象相吻合[11,32].多孔薄板拉伸將形成明顯滑移帶,交界處即兩個(gè)主導(dǎo)滑移系競(jìng)爭(zhēng)最激烈的區(qū)域.另外,對(duì)于[100]取向薄板冷卻孔數(shù)量的變化并沒影響主導(dǎo)滑移系,均為 ξ2,ξ5,ξ8和ξ11;對(duì)于[110]取向冷卻孔數(shù)量變化強(qiáng)烈影響了主導(dǎo)滑移系,從單孔的 ξ1,ξ2,ξ4,ξ5變?yōu)?ξ7,ξ8,ξ10,ξ11.此外,兩個(gè)取向薄板的滑移帶均由多個(gè)滑移系共同主導(dǎo),不同滑移系的滑移方向不一致也導(dǎo)致了實(shí)驗(yàn)[11,25]中所觀察到的次級(jí)裂紋的產(chǎn)生(圖14),使得裂紋呈現(xiàn)彎折的形狀.

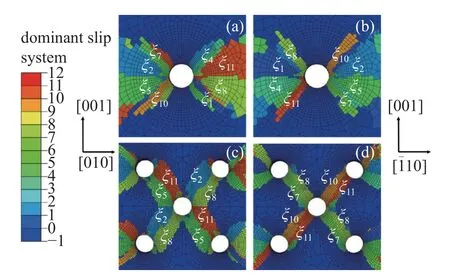
圖13 應(yīng)變?yōu)?%時(shí)主導(dǎo)滑移系: (a),(c) [100];(b),(d) [110]Fig.13 Dominant slip system at 2% strain: (a),(c) [100];(b),(d) [110]

圖14 單孔(a) [100]薄板和(b) [110]薄板滑移帶[11]Fig.14 The slip band for (a) [100] and (b) [110] plates with a hole[11]

在實(shí)驗(yàn)中已報(bào)道兩個(gè)取向薄板的抗拉強(qiáng)度不同[11,47],后續(xù)通過對(duì)比兩者塑性滑移特征解釋強(qiáng)度差異原因.圖15 為4 個(gè)節(jié)點(diǎn)在不同變形階段的總塑性滑移量以及塑性滑移的標(biāo)準(zhǔn)差.對(duì)于單孔薄板,節(jié)點(diǎn)至孔距離的影響大于取向的影響.節(jié)點(diǎn)位置離孔越近,累積塑性滑移量越大且離散程度越強(qiáng).取向?qū)τ谒苄曰屏坑绊懖淮?如圖15(a)所示;但是取向?qū)τ谒苄曰频碾x散程度影響較大,如圖15(c)所示.而對(duì)于多孔薄板,次級(jí)取向的影響更為明顯,[110]取向兩個(gè)節(jié)點(diǎn)在2%應(yīng)變時(shí)塑性滑移量均大于[100]取向,如圖15(b)所示;且[110]取向4 節(jié)點(diǎn)處的塑性滑移離散程度均遠(yuǎn)大于[100] 取向,如圖15(d) 所示.上述結(jié)果表明單孔和多孔的[110]取向薄板相比于[100]取向塑性滑移量和離散程度均更大,更易發(fā)生塑性變形.符合實(shí)驗(yàn)所觀察到的次級(jí)取向?qū)е碌膹?qiáng)度差異現(xiàn)象[11],如圖16 所示.

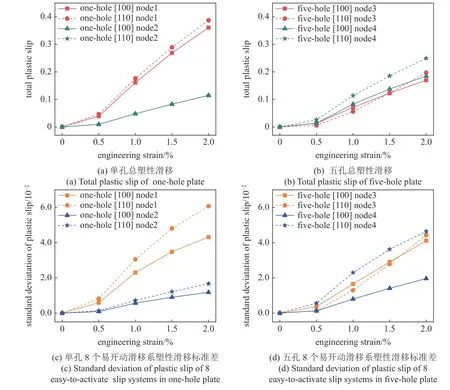
圖15 不同變形階段塑性滑移特征Fig.15 Plastic slip characteristics in different deformation stages

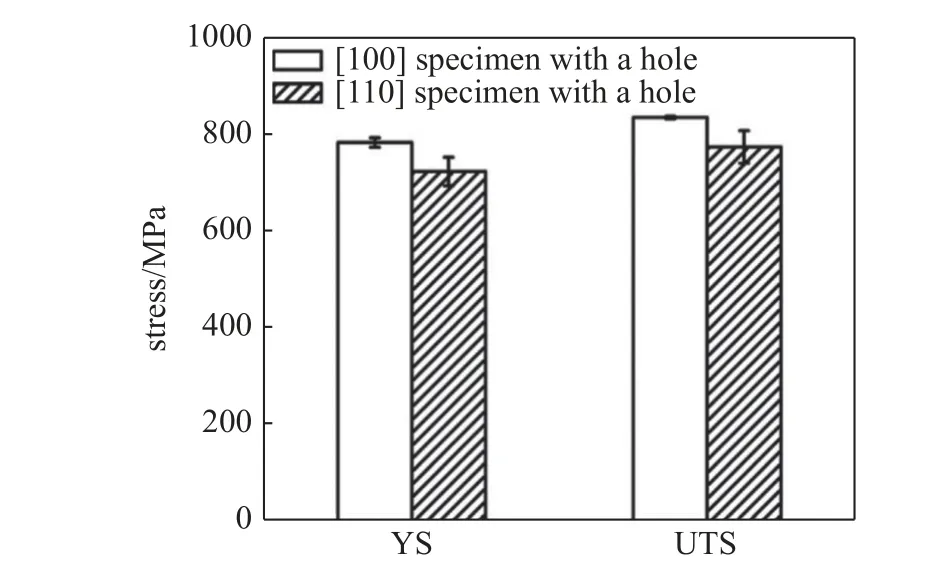
圖16 不同次級(jí)取向單孔薄板的屈服強(qiáng)度和極限拉伸強(qiáng)度[11]Fig.16 Yield stress and ultimate tensile strength of plates with a hole in different secondary orientations[11]

3.5 非均勻變形

由于引入幾何必需位錯(cuò)協(xié)調(diào)變形才能發(fā)生晶格轉(zhuǎn)動(dòng)和滑移系的非均勻開動(dòng)[32,48].在實(shí)驗(yàn)以及模擬中也都發(fā)現(xiàn)了冷卻孔附近具有較強(qiáng)的晶格轉(zhuǎn)動(dòng)[32],因此使用幾何必需位錯(cuò)密度可以合理描述冷卻孔附近的非均勻變形.如圖17 所示,當(dāng)應(yīng)變?yōu)?%時(shí),單孔薄板中的幾何必需位錯(cuò)主要集中在孔兩側(cè),表明鎳基合金板在拉伸過程中主要在孔兩側(cè)發(fā)生非均勻變形;多孔薄板幾何必需位錯(cuò)密度分布于孔附近以及滑移帶區(qū)域,表明滑移帶中也存在非均勻變形.相比于多孔薄板,單孔中局部幾何必需位錯(cuò)更大,導(dǎo)致孔周圍應(yīng)力集中更明顯(圖18),使裂紋更早萌生.根據(jù)滑移阻力公式(14)可得冷卻孔附近的幾何必需位錯(cuò)對(duì)滑移阻力的貢獻(xiàn)約為73.5 MPa,占比最大分切應(yīng)力380 MPa 的20%左右.

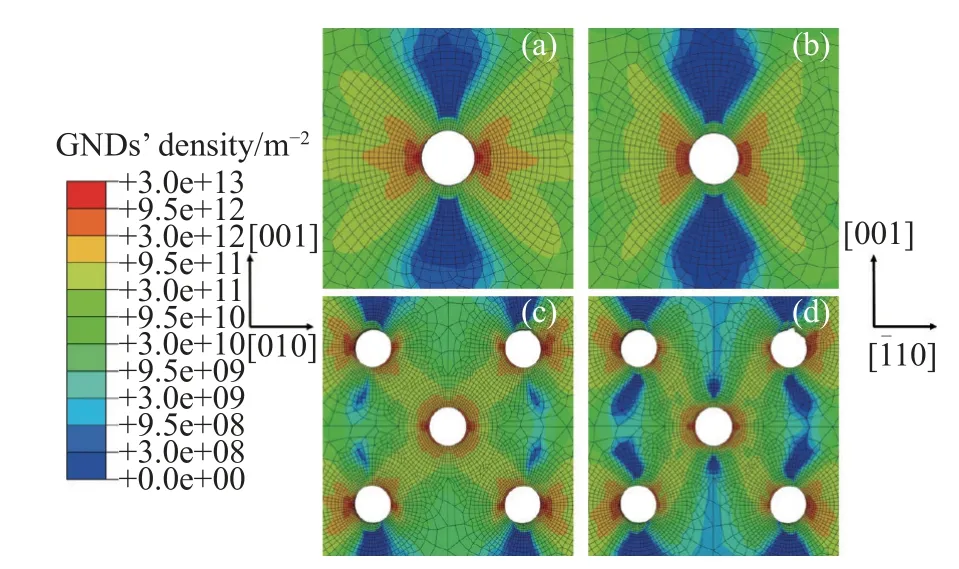
圖17 應(yīng)變?yōu)?%時(shí)幾何必需位錯(cuò)密度分布: (a),(c) [100];(b),(d) [110]Fig.17 Geometrically necessary dislocation density distribution at 2%strain: (a),(c) [100];(b),(d) [110]

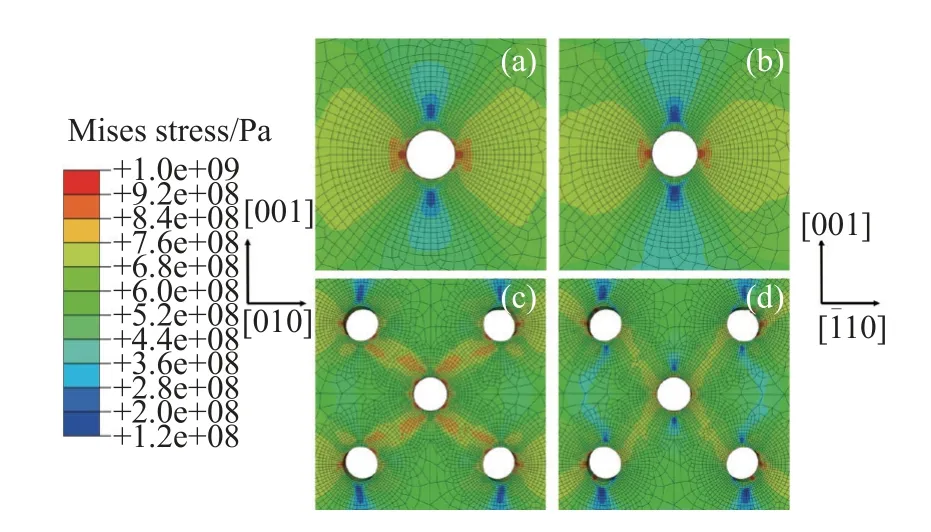
圖18 應(yīng)變?yōu)?%時(shí)Mises 應(yīng)力分布: (a),(c) [100];(b),(d) [110]Fig.18 Mises stress distribution at 2% strain: (a),(c) [100];(b),(d) [110]

如圖19 所示,多孔薄板節(jié)點(diǎn)處幾何必需位錯(cuò)密度在變形階段均小于單孔,且次級(jí)取向?qū)τ趲缀伪匦栉诲e(cuò)的影響小于冷卻孔數(shù)量的影響.多孔[110]取向4 節(jié)點(diǎn)處幾何必需位錯(cuò)增殖較快且在0.6%附近發(fā)生陡增,這是由于此處滑移系開動(dòng)數(shù)量少(僅 ξ10,ξ11兩個(gè)主滑移系開動(dòng))而滑移量較大,導(dǎo)致幾何必需位錯(cuò)密度增殖較快從而協(xié)調(diào)不均勻變形.

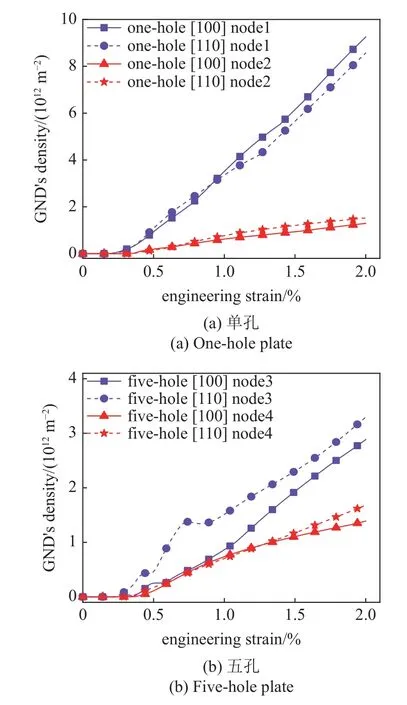
圖19 幾何必需位錯(cuò)密度隨應(yīng)變的演化Fig.19 Evolution of geometrically necessary dislocation density with increasing strain

4 結(jié)論

本文基于非局部晶體塑性有限元模擬研究了單孔和多孔薄板次級(jí)取向?qū)τ趩尉ф嚮辖鹚苄宰冃蔚挠绊?主要結(jié)論如下.

(1)次級(jí)取向主要影響塑性滑移區(qū)分布區(qū)域以及滑移系開動(dòng)模式,[100]取向薄板相比于[110]取向開動(dòng)滑移系數(shù)量更多、主滑移系塑性滑移量及其離散程度更小,使得[100]取向強(qiáng)度高于[110]取向.

(2)單孔薄板受取向影響較小,而多孔薄板孔洞之間具有強(qiáng)烈的相互作用,從而產(chǎn)生明顯的塑性滑移帶,且塑性滑移帶受取向影響較大.同時(shí)冷卻孔的存在使得分切應(yīng)力在變形過程中發(fā)生波動(dòng),抑制了部分滑移系開動(dòng).并且主導(dǎo)滑移系之間的競(jìng)爭(zhēng)使得裂紋擴(kuò)展呈彎折形狀.

(3)冷卻孔數(shù)量的增多將協(xié)調(diào)非均勻變形.相比于多孔薄板,單孔附近幾何必需位錯(cuò)更大,導(dǎo)致孔周圍應(yīng)力集中更明顯,使裂紋更早萌生.