雙通道旋轉輸流管臨界流速和振動模態分析1)

張 博 鄭昊楷 孫東生 丁 虎 陳立群,3)

* (長安大學理學院,西安 710064)

? (上海大學力學與工程科學學院,上海 200444)

引言

航空發動機是飛機的心臟,是國家工業基礎、科技水平和國防實力的重要標志.渦輪葉片是航空發動機中最重要的關鍵部件之一,其可靠性直接影響發動機能否正常.已有研究表明[1-4],航空發動機故障原因中62%以上是由于渦輪葉片振動過量,且由于高溫、高壓工況下通過蛇形冷卻通道進行降溫的設計,葉片通道內部受到科氏力、離心力等因素的相互作用,具有復雜的流固耦合效應.因此,研究含蛇形冷卻通道的旋轉葉片動力學特性,對發動機葉片的合理化設計與減振降噪具有重要意義.

由于旋轉葉片結構在工程中的廣泛應用,尤其是在航空發動機領域的核心地位,從上世紀四50 年代以來,旋轉葉片的動力學行為研究吸引了國內外學者的廣泛關注.如Carnegie[5]在1959 年首次研究了旋轉葉片的自振頻率.張偉等[1]將葉片簡化為功能梯度材料薄壁梁,通過伽遼金法研究了系統在空氣熱彈性載荷下的動力學行為.此外,許多學者[6-11]將葉片簡化為大變形柔性薄板.如趙飛云等[12]基于連續介質力學理論和Jourdain 速度變分原理,研究高速旋轉下的柔性矩形薄板的耦合動力學模型.鄭彤等[13]、蔣建平等[14],利用Langrage 方程法得到系統的一次近似耦合動力學方程.

以上研究,將旋轉葉片簡化為旋轉的懸臂梁或旋轉的大變形柔性薄板,但均未考慮內部流體對葉片動力學特性的影響.由前人的研究[15-21]可知內部流體會對葉片的振動產生復雜的影響,將葉片簡化為旋轉懸臂輸液管模型可以從宏觀上更深入地研究流體的某一特性對旋轉葉片的動力學影響.Chen[22]在1971 年對輸送脈動流體的管道振動進行研究,并通過數值方法確定穩定性邊界.Paidoussis[23]在1987 年對輸液管的振動作了詳細的論述,并指出發散失穩和顫振失穩兩種值得深入研究的現象.后續有Rousselet 等[24]、Lundgren 等[25-27]和徐鑒等[28-29]先后導出了懸臂輸液管的非線性運動方程.

Paidoussis 等[30]、黃玉盈等[31]和Ibrahim[32-33]分別在1993 年、1998 年和2010 年對輸液管模型動力學模型的研究現狀進行了詳細的綜述.王乙坤等[34]研究了脈動內流作用下的輸液管振動問題.Wang等[35]用牛頓法和龍格-庫塔法對波紋輸液管的動力學行為進行理論和數值分析,發現波紋總數和波紋幅度對輸液管的動力學行為有較大影響.宮亞飛等[36]利用哈密頓原理和伽遼金法推導了含有初始彎曲的功能梯度輸液管的非線性動力學方程,分析超臨界功能梯度輸液管的自由振動特性.Oh 等[37]利用瑞麗利茲法推導含冷卻通道的旋轉葉片的熱彈動力耦合模型,研究冷卻效應下系統的固有頻率與拉伸特性.張博等[38]基于Langrage 原理和假設模態法研究不同端部集中質量、轉速對旋轉輸液管臨界流速的影響及特定參數組合下的內共振現象.

通過文獻調研不難發現,在內冷葉片研究領域,考慮內流作用對系統振動特性影響的報道較少,文獻[38]中雖開展了相關研究,但只局限于單冷卻通道模型.為了更貼合包含多條冷卻通道且通有流體介質的先進內冷葉片工程實例[39],本文在文獻[38]基礎上,引入葉片換熱特性研究[40]中對內部通道的簡化方式,將葉片簡化為含雙輸液通道的旋轉懸臂輸液管,采用能量法建立其動力學模型,揭示包含多條冷卻通道的旋轉葉片結構中,冷卻通道內流體流動對葉片動力學特性的影響規律.

1 動力學方程推導

本文將含蛇形冷卻通道的渦輪葉片簡化為如圖1 所示長為L的兩通道旋轉懸臂輸流管,固接在半徑r的中空圓柱上以常數Ω旋轉,截面高為h,寬為b,單位長度質量為m,兩通道半徑均為r0,兩通道軸線與輸流管軸線距離均為d,兩通道內流體的單位長度質量分別為M1,M2,相對通道的流速分別為常數U1與U2.以中空圓柱中心O點為原點,建立全局坐標系XYZ,單位方向向量分別為i,j,k.以輸流管中軸線與圓柱側面的交點為o點,沿軸線方向為x軸,建立隨轉坐標系xyz,單位方向向量分別為i′,j′,k′,軸線上任意一點在t時刻的x,y方向位移分量分別用w1(x,t)和w2(x,t)表示,由變形引起的轉角為θ.為了簡化分析,引入以下假設: (1)忽略輸流管剪切變形和轉動慣量的影響;(2)忽略輸流管在z方向的變形,即振動發生在XY平面內;(3)兩通道內的流體均為為定常不可壓縮的無黏流體;(4)輸流管是均勻、各向同性的線彈性材料.

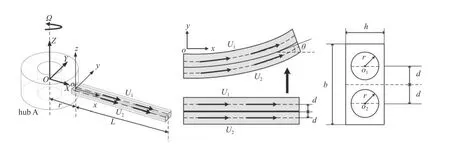
圖1 含兩通道的旋轉輸流管Fig.1 Sketch of a rotating cantilever double channel pipe

在全局坐標系下,輸流管上任意一點的速度矢量為

令y=0 可表示輸流管中軸線上任意一點的速度矢量為

則輸流管的動能為

輸流管因旋轉運動而產生的軸向收縮勢能[41]為

輸流管的變形勢能為

式中,EI為輸流管的抗彎剛度,Ap為截面面積.在全局坐標系下,兩通道內流體的速度分別為

兩通道內流體的動能為

根據Euler-Bernoulli 梁理論,在隨轉坐標系下,通道1(y=d)和通道2(y=?d)中軸線上任意一點的位置矢量為

在輸流管開放系統中,輸流管做無窮小變形運動下,流體對輸流管做的功可由文獻[42]得

則旋轉輸流管開放系統的Lagrange 函數為

本文兩通道旋轉懸臂輸流管的邊界條件為

應用假設模態法離散系統的兩個變形分量

式中,qi(t) 代表系統在相應方向的廣義位移,N1,N2為選取的模態函數個數,?i(x)為滿足系統位移邊界條件的模態函數

其中參數βl為頻率方程 c os(βlL)ch(βlL)=?1的根.

根據Lagrange 原理,得到系統矩陣形式的動力學方程

為了使研究結果具有普遍性,定義以下無量綱參數

其中,α0,α1,α2分別表示輸流管及兩通道內流體的單位長度質量權重;τ,κ,Ω*分別表示無量綱時間、長細比與無量綱轉速;u1和u2分別表示兩通道中流體的無量綱流速.

得到無量綱化后的系統動力學方程為

其中質量子陣、阻尼子陣、陀螺子陣、剛度子陣和廣義力子陣見附錄.

2 復模態分析

采用降階擴維的方法求解系統的特征值,為簡化方程,引入以下向量與矩陣

由于本文研究的是自由振動問題,方程可簡化為

設其通解為

將其代入式(22),得到關于實值矩陣的一般特征值問題

求解得到系統呈復共軛出現的特征根和特征向量

式中,σr為阻尼因子,ωr為固有頻率.因此,特征矢量矩陣為

由式(16)、式(29)與式(30)可得輸液管橫向位移的第r階模態響應為

式中單劃線與雙劃線部分分別代表了阻尼因子和相位變化對輸流管橫向位移模態響應的影響,為表述方便,下文使用符號和分別表示上述兩因素歸一化模態.

3 收斂性研究與對比驗證

本文的系統參數選取參考文獻[38],在后文中,若無特別說明,系統的無量綱參數設置為:α0=0.675,α1=0.1625,α2=0.1625,γ=0.5,κ=61.94,Ω*=5,δ=0.012.

圖2 研究了假設模態法的收斂性,在不同試探函數個數下,系統的特征根軌跡圖相似,臨界流速數值存在微小差別.當試探函數個數取15 時,臨界流速收斂.在后文的數值算例中均取N1=N2=15.由圖可知,當流體流速較小時,流體引起了系統各階模態的阻尼效應.隨著流速的增加,第1 和3 階模態軌跡相繼穿越橫軸,預示著輸流管1 階和3 階模態將發生顫振失穩,但第2 階模態始終未發生失穩.

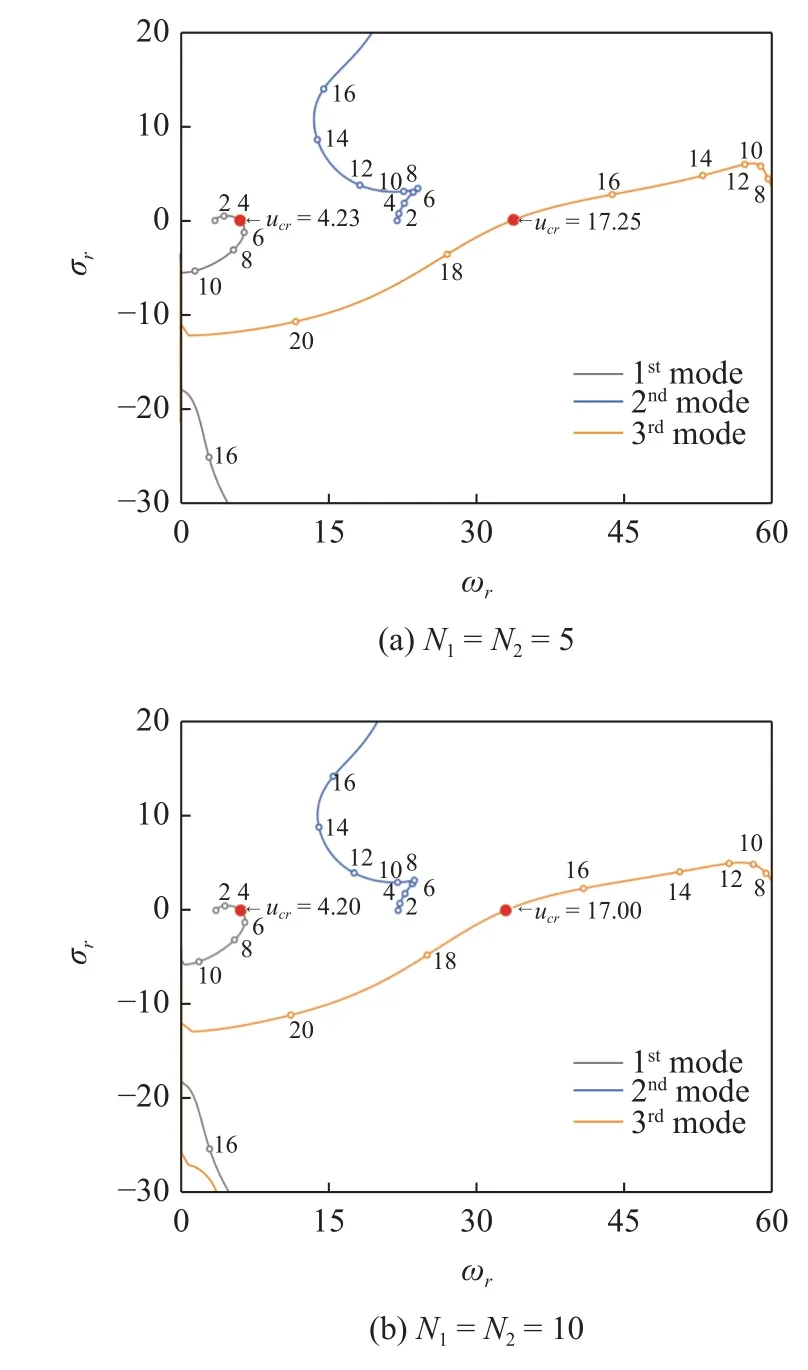
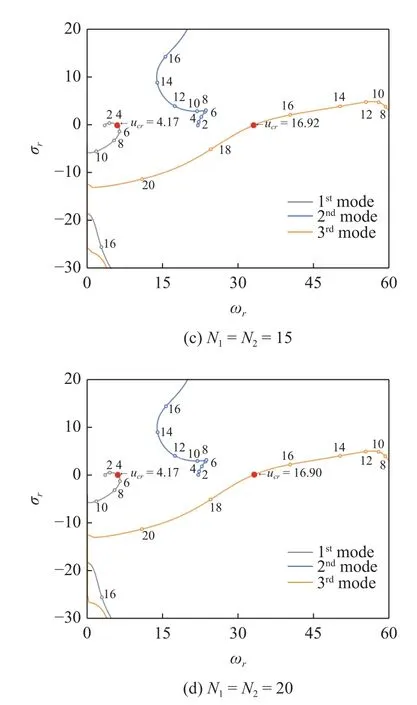
圖2 不同試探函數個數下前3 階特征根軌跡曲線 (Ω*=0)Fig.2 The trajectories of the first three eigenvalues for different trail function numbers (Ω*=0)

以文獻[43]中兩端簡支的單通道輸流管系統為研究對象,得到該系統的前兩階特征根軌跡曲線,如圖3 所示.將所得的前兩階臨界流速與文獻[43]的結果相比較,如表1 所示,兩者結果吻合,驗證了本文建模方法的正確性.

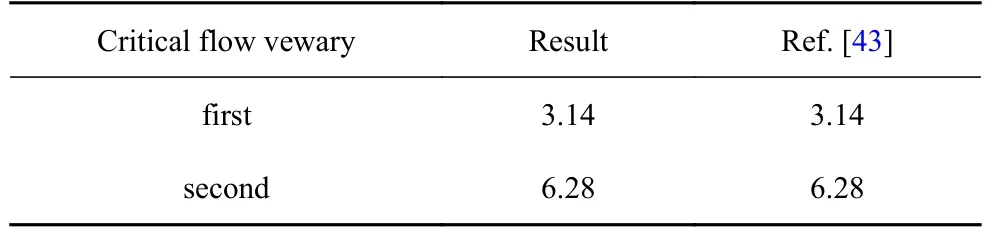
表1 兩端簡支單通道輸流管系統的前兩階臨界流速對比Table 1 Comparison of the first two critical flow velocities for simply supported flow pipe

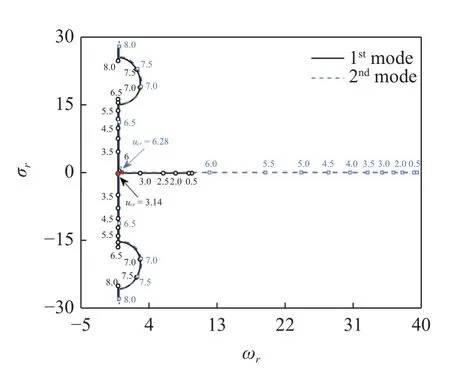
圖3 兩端簡支的單通道輸流管系統的前兩階特征根軌跡Fig.3 The trajectories of the first two eigenvalues for simple supported flow pipe

4 結果分析與討論

采用雙通道模型更貼合含多條冷卻通道的先進內冷葉片工程實際,在此基礎上開展的動力學特性研究更具有參考價值.圖4 對比了單位時間流量相同時,中心單通道模型與對稱雙通道模型的系統臨界流速值.其中,單通道的截面半徑為(r0為雙通道模型的截面半徑),兩模型的長細比分別為κsingle=59.75,κtwin=74.05,其余參數與前文一致.由圖可見,在不同轉速下,雙通道模型的臨界流速值均大于單通道模型,且隨著轉速的增加,雙通道模型的臨界流速值也比單通道模型增長得更快.

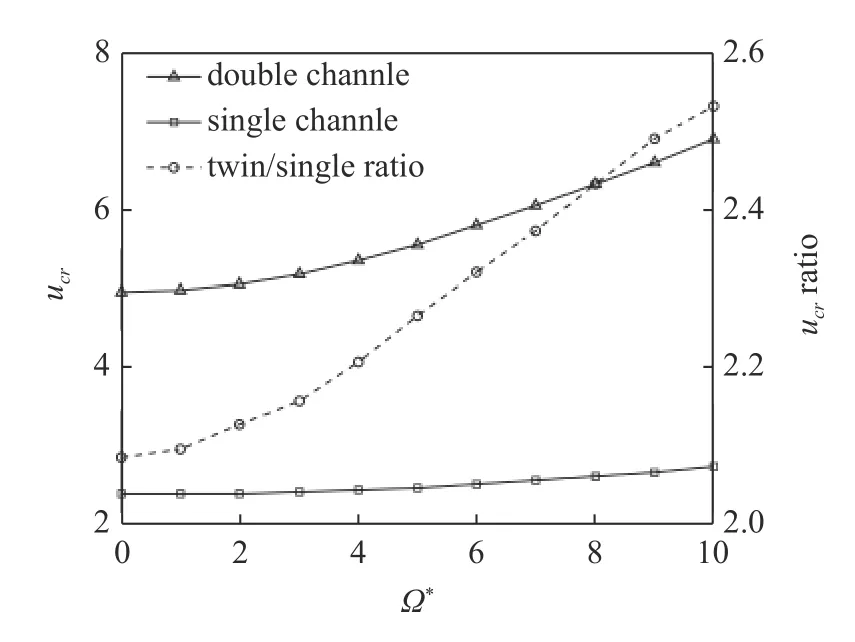
圖4 單、雙通道模型的臨界流速隨轉速的變化曲線Fig.4 The curves of critical flow velocity with rotating speed for the single/twin-channel models

圖5 研究了無量綱流速u1和u2的比例分別為1:1,1:2,1:3,1:4 時系統的特征根軌跡圖,其中圖中所標識的流速代表通道2 中流體流速.可以發現在不同流速比值下,得到的系統特征根軌跡圖曲線形狀大致相同,隨著比值減小,第1 階模態和第3 階模態在發生失穩時的臨界流速值增大,第2 階模態始終未發生失穩.

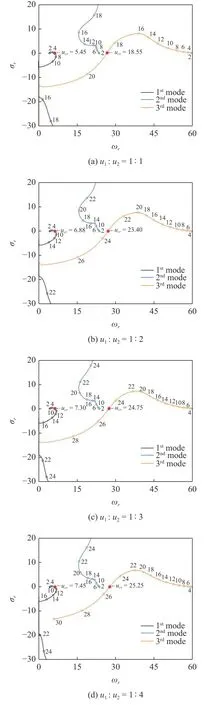
圖5 不同流速比下前3 階特征根軌跡(ucr=u2,Ω*=5)Fig.5 The trajectories of the first three eigenvalues for different velocity ratios (ucr=u2,Ω*=5)

從系統的動力學方程不難發現,通道內流體的流動與管道整體的旋轉運動均會給系統引入陀螺效應,即本文建立的動力學模型為典型的雙陀螺系統.圖6 研究了轉速對系統特征根軌跡的影響.由圖6 可見,轉速第1 階模態的特征根軌跡影響較小,并始終只存在一個臨界流速.而隨著轉速的提高,系統的第2,3 階特征根軌跡繞圈現象越來越顯著,并會多次穿越虛軸,預示流速變化過程中系統的第2,3 階模態將經歷失穩→穩定→失穩的復雜動力學歷程,產生該現象是由于旋轉運動引入的陀螺效應對系統響應的影響.為了進一步研究這一現象,控制轉速不變,在圖7 中繪制了系統特征根軌跡隨長細比的演變規律.可以發現,隨著κ增大,系統第2,3 階模態特征根軌跡的繞圈現象逐漸消失,當κ足夠大時,第2 階模態不再發生失穩,第3 階特征根軌跡只穿越一次虛軸,只存在一個臨界流速,類似于經典的懸臂輸流管模型[15].實際上,隨著κ增大,旋轉運動引起的管道軸向與橫向間的陀螺耦合效應逐漸減弱[44],系統雙陀螺效應中通道內流體的流動引起的陀螺效應成為主導因素,因而系統表現出類似非旋轉的懸臂輸流管的動力學行為.

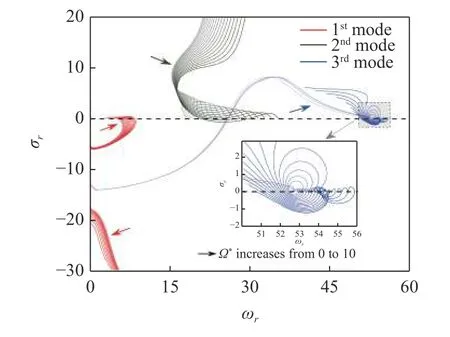
圖6 不同轉速下前3 階特征根軌跡曲線(κ=35)Fig.6 The trajectories of the first three eigenvalues for different rotating speeds (κ=35)

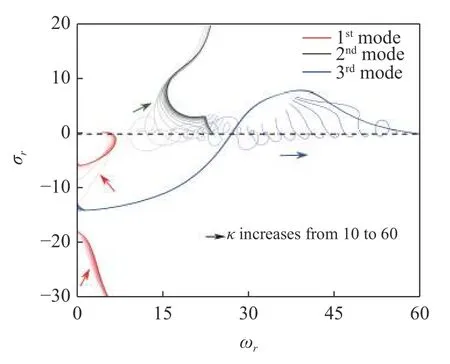
圖7 不同長細比下前3 階特征根軌跡曲線(Ω*=5)Fig.7 The trajectories of the first three eigenvalues for different slenderness ratios (Ω*=5)

圖8 揭示了相位變化對輸流管橫向位移前3 階模態響應的影響.由圖可見,陀螺效應使得系統不同位置的響應出現相位差.與實模態系統振動呈現駐波特性不同,復模態系統振動呈現出行波特性,即出現“節點”移動現象.

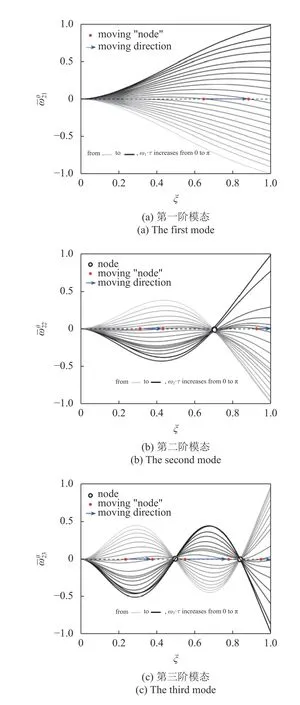
圖8 相位變化對前3 階模態響應的影響(u1=u2=8,Ω*=10)Fig.8 The curves of the first three modal responses for different phase changes (u1=u2=8,Ω*=10)

圖9(a)～ 圖9(c)給出了3 組不同流速和轉速組合下,阻尼因子對輸流管橫向位移前3 階模態響應的影響.當u1=u2=6,Ω*=15 時,前3 階模態響應的幅值均隨時間減弱;當u1=u2=10,Ω*=12 時,前3 階模態響應的幅值隨時間分別增強、減弱、減弱;當u1=u2=15,Ω*=15 時,前3 階模態響應的幅值隨時間分別增強、增強、減弱.這表明在不同的流速和轉速組合下,系統不同階模態響應會出現不同的增強或減弱現象.

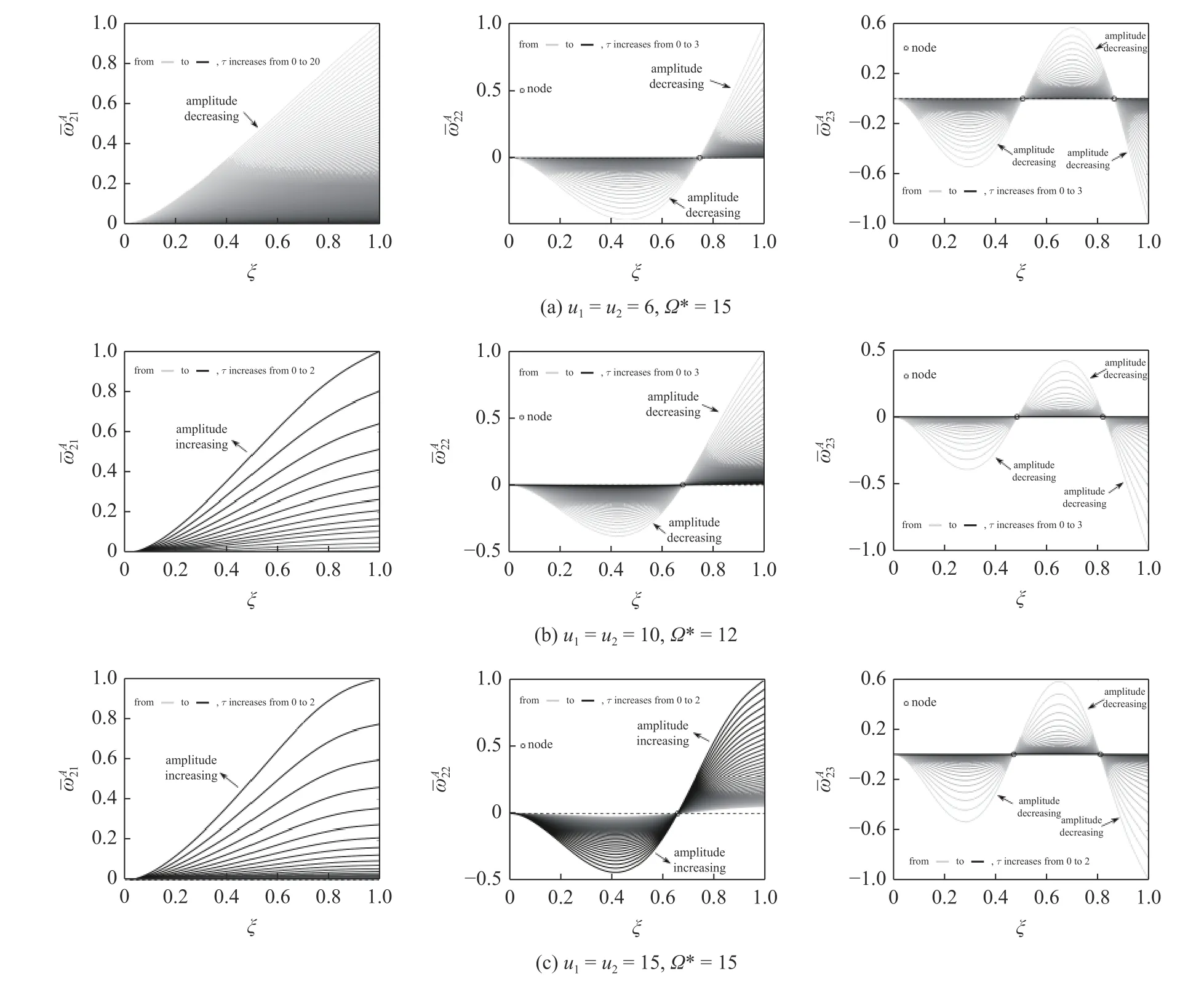
圖9 不同流速和轉速下阻尼因子對前3 階模態響應的影響Fig.9 The effects of damping factor on the first three mode responses for different flow rates and rotating speeds

5 結論

本文通過能量法建立了含兩通道的旋轉輸流管動力學控制方程,通過與文獻結果對比驗證了本文方法的正確性,研究了流體單位長度質量、不同流速比和輸流管長細比對系統臨界流速的影響,并分別分析了相位變化與阻尼因子對前3 階模態響應的影響,得出了以下結論.

(1)在單位時間流量相同時,雙通道模型的臨界流速值大于單通道模型的,且隨著轉速的增大,雙通道模型的臨界流速值增長得更快;

(2)隨著兩通道內流速比值減小,第1 階模態和第3 階模態在發生失穩時的臨界流速值增大,且第2 階模態始終未發生失穩;

(3)旋轉運動引入的陀螺效應對系統第1 階特征根軌跡影響較小,但會顯著影響第2,3 階特征根軌跡,使其發生繞圈現象,并多次穿越虛軸,從而導致第2,3 階模態振動存在多個臨界流速.

(4)輸流管橫向位移模態響應出現相位差,呈現出行波特性,即出現"節點"移動現象,在不同的流速和轉速組合下,系統不同階模態響應會出現不同的增強或減弱現象.

本文首次研究了含兩通道的旋轉輸流管動力學特性,為含復雜冷卻通道布局的旋轉葉片的設計提供一定理論參考.但本文中只考慮兩通道為簡單的對稱式布局,輸流管內部復雜不對稱的通道布局等情況有待進一步的研究與討論.

附錄