SVD分解在口腔手術機器人手眼標定中的應用

李恒，陳鑄，羅陽，伍劍波，方輝

(四川大學機械工程學院，四川成都 610041)

0 前言

隨著機器人技術的發展，機器人被越來越多地應用到醫療行業。其中手術機器人是未來醫療機器人中的主要門類[1]。而手術導航系統的手眼標定問題是手術機器人研究中十分重要的課題，手眼標定的精度將直接影響手術機器人工作的精度。根據調研可知：進行口腔手術的機器人導航系統位置定位精度至少在0.5 mm以下，姿態定位精度至少在1°(即17 mrad)以下。

手眼標定問題目前可分為兩類：一類是Eye-to-Hand(固定視點)，一類是Eye-in-Hand(非固定視點)。前者的傳感器與機器人分離，兩者分別固定，工作時傳感器保持靜止；后者的傳感器固定于機器人末端，工作時傳感器隨機器人末端移動[2-3]。相較于Eye-in-Hand系統，Eye-to-Hand系統的傳感器始終靜止，更容易實現高精度、高穩定的導航，因此目前大多數口腔手術機器人均采用Eye-to-Hand系統。

手眼標定問題的核心為求解傳感器坐標系和機器人坐標系之間的旋轉矩陣和平移向量。其相關算法國內外均有大量的研究與成果，最早由SHIU和AHMAD[4]將該問題轉化為解齊次方程AX=XB的問題。圍繞求解AX=XB， TSAI和LENZ[5]提出了兩步法，先計算出手眼標定中的旋轉矩陣，再利用旋轉矩陣求解平移向量。文獻[6-7]通過李群代數、對偶四元數相關數學工具，同時求解了旋轉矩陣和平移向量。前面所述算法都需要傳感器能夠同時精確測量標志物的位置和姿態信息。

由雙目視覺姿態測量原理可知：其姿態定位精度低于位置定位精度，且其姿態精度難以控制(與標志物形狀有關)。當雙目視覺相機測量的姿態數據誤差較大時，仍使用姿態數據進行手眼標定，必然帶來較大的標定誤差。在這種情況下，文獻[8]采用最近點迭代算法，但迭代時給出的初始值可能導致迭代進入局部最優解，且迭代過程較長。文獻[9]通過剛體變化算法分別計算旋轉矩陣和平移向量，但需要人工操作視覺定位球的球心與機器人TCP重合，難以保證精度。文獻[3]通過簡單的3次純平移與1次純旋轉過程，計算旋轉矩陣和平移向量，但采集和用于計算的數據較少，該方法的精度有限。

本文作者闡述一種無需測量視覺標志物姿態數據的口腔手術機器人手眼標定算法，通過多次采集純平移與純旋轉過程中的數據，借助非奇異值分解的數學工具計算傳感器坐標系與機器人基座坐標系之間的旋轉矩陣與平移向量。

1 口腔手術機器人手眼標定數學模型

在機器人的末端夾持手術所使用的工具并定義該工具的工作點為機器人的TCP，并將視覺識別標志物與工具相對固定，雙目視覺在機器人的外部固定，如圖1所示。

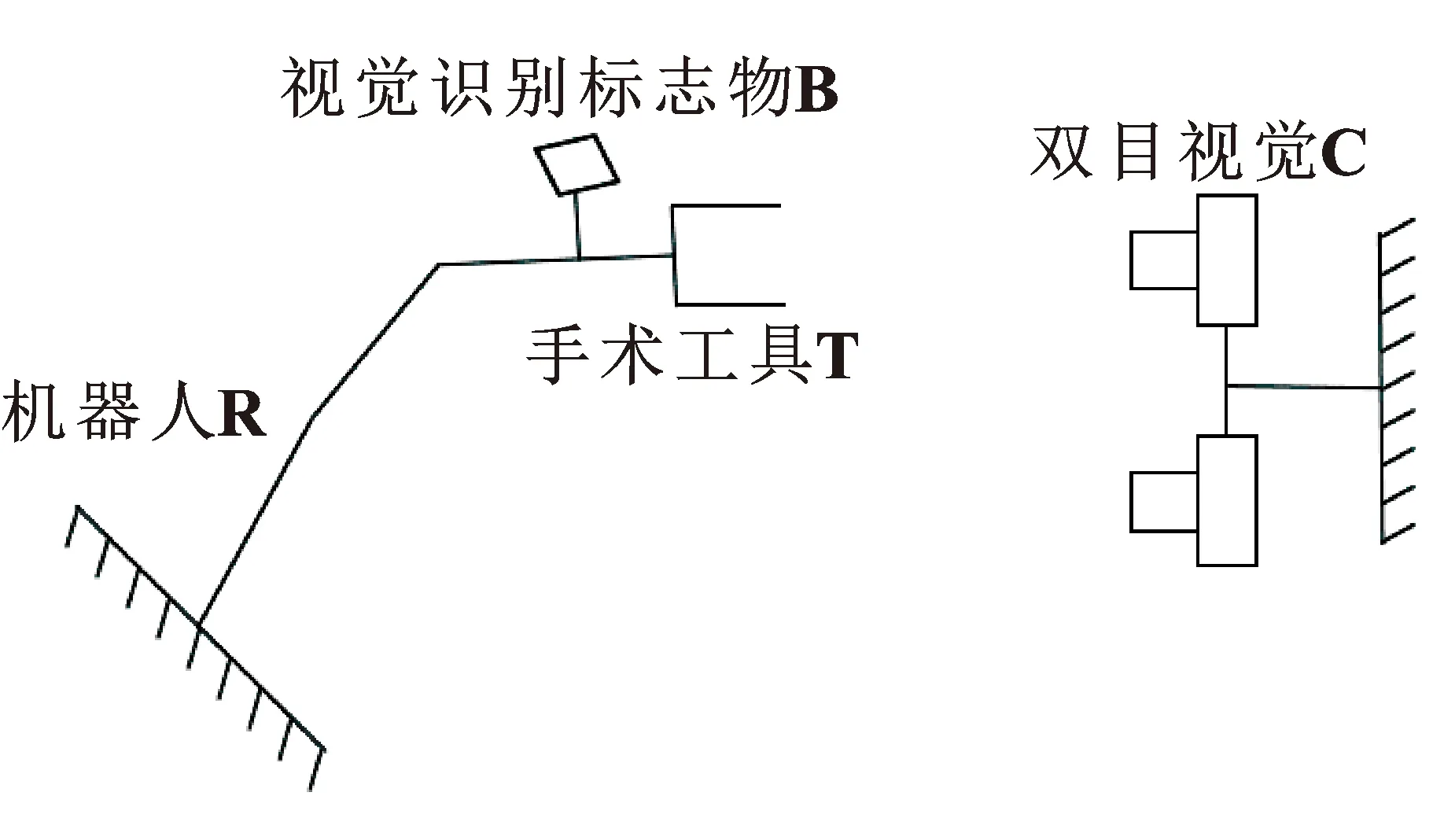
圖1 手術機器人系統示意Fig.1 Surgical robot system

(1)

將式(1)分解后可得到如下齊次方程組：

(2)

2 基于SVD分解的剛體變換算法

文獻[10]提出了基于SVD分解的剛體變化算法計算兩組對應點集之間的旋轉矩陣和平移向量。

設有兩組d維點集P={p1,p2，…，pn}和Q={q1，q2，…，qn}，其中p1和q1，p2和q2，…,pn和qn兩兩相互對應。通過最小二乘法可得下列函數：

(3)

式中：R為點集P和點集Q對應的旋轉矩陣；t為點集P和點集Q對應的平移向量；ωi為兩點集每個對應點的權重，常設為1，ωi>0。

第一步，分別計算兩組點集的重心。

(4)

第二步，將點集P、Q中每個元素減去重心，得到兩個新的點集X、Y。

(5)

第三步，將X、Y中的點集組成d×n的矩陣，分別為X、Y,將每對點集的權重組成對角矩陣W。

(6)

(7)

第四步，計算兩組新點集與權重矩陣的協方差矩陣。

S=XWYT

(8)

第五步，對S進行SVD分解。

S=UΣVT

(9)

第六步，計算旋轉矩陣R和平移向量t。

(10)

(11)

采用了上述方法進行手眼標定時，由于雙目視覺獲取的是視覺標志物的點集，機器人獲取的是TCP的點集，而視覺識別標志物點集與TCP點集并不對應，文獻[9]人工將視覺標志球球心與機器人的TCP重合，但該方法操作難度大，因此最終標定結果并不理想。

3 基于SVD分解的手眼標定算法

觀察式(5)，將原始點集的每一個元素減去點集的重心后構成新的點集，兩組新點集坐標系之間的坐標系原點重合。

而對于口腔手術機器人，視覺識別標志物與手術工具工作點TCP之間的旋轉矩陣和平移向量隨結構的固定而確定。在對應點采集過程中如果保持手術工具只進行純平移運動，視覺識別標志物的空間點坐標與TCP空間點坐標之間始終相差一個固定的平移向量t，設為

t=[t1,t2,t3]

(12)

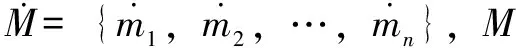
則在平移過程中采集的TCP在機器人基座坐標系下的坐標點集為N={n1，n2，…，nn}，則根據式(12)可得：

(13)

(14)

(15)

(16)

(17)

且：

(18)

綜合式(17)和式(18)可得：

(19)

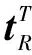
首先控制機器人以TCP為圓心進行旋轉，旋轉過程中采集一系列視覺識別標志物在雙目視覺坐標系下的坐標點集H={h1，h2，…，hn}。設此時TCP在雙目視覺坐標系下的坐標為

g=[gx,gy,gz]

(20)

則有：

(hix-gx)2+(hiy-gy)2+(hiz-gz)2=d2

(21)

式中：hix為第i個采集點的x值；hiy為第i個采集點的y值；hiz為第i個采集點的z值；d為采集點到圓心的距離。

共有n個方程，將i≥2的方程減去i=1的方程，可得：

(22)

共有n-1個上述方程，轉化為矩陣形式，即為

Ag=B

(23)

式中：

由于A為(n-1)×3的矩陣，無法直接求逆，通過SVD分解計算A的偽逆A+。

則：

g=A+B

(24)

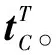
4 手術導航系統手眼標定過程描述

文中所介紹的手眼標定過程如下：

第一步，控制機器人進行若干次(至少兩次)純平移運動，每次運動完通過雙目視覺重復采集視覺識別標志物的坐標，計算平均值，同時通過機器人控制器重復采集TCP坐標，計算平均值。從而獲得點集M與N。

第三步，控制機器人以TCP為球心，進行若干次(至少3次)純旋轉運動，每次運動完成后通過雙目視覺重復采集視覺識別標志物的坐標，計算平均值，從而獲得點集H。

5 仿真

設計驗證上述算法的仿真實驗。在該實驗中，設定雙目視覺相機在機器人坐標系下的姿態以旋轉矢量法表示，其中Rx=0.3 rad，Ry=1.6 rad，Rz=0.5 rad，雙目視覺在機器人坐標系下的坐標x=600 mm、y=700 mm、z=1 000 mm，TCP在視覺識別標志物坐標系下的坐標x′=200 mm、y′=0 mm、z′=0 mm，平移時視覺識別標志物坐標系與雙目視覺坐標系完全平行。同時仿真中設定雙目視覺坐標系下視覺識別標定板在x、y、z各個方向的讀數誤差均值為0 mm、標準差0.12 mm的正態分布隨機誤差；機器人基座坐標系下TCP的x、y、z各個方向上的讀數誤差為均值0、標準差0.1 mm的正態分布隨機誤差。

由于該算法中需要進行多次純平移運動和多次純旋轉運動，根據算法過程純平移采集點個數影響標定誤差的旋轉部分和平移部分，而純旋轉采集點個數只對平移部分產生影響，仿真實驗時設定純旋轉次數為6次(共7個點)，對比不同純平移次數下計算的標定誤差(手眼標定算法計算旋轉矢量和平移向量與理論的旋轉矢量和平移向量之間的差值)。仿真實驗結果如表1所示。

表1 仿真實驗標定誤差Tab.1 Calibration error of simulation experiments

由表1中可以看出：在上述仿真實驗條件下，標定誤差的平移誤差隨著純平移采集點個數的增加并沒有明顯的提升；而旋轉誤差隨著采集點的增加而明顯減少。且在純平移采集點為8個、純旋轉采集點7個的情況下，仿真實驗表明平均平移誤差為0.101 mm，最大平移誤差為0.173 mm，平均旋轉誤差為0.07 mrad，最大旋轉誤差為0.14 mrad。上述實驗驗證了該手眼標定算法的有效性，下一步將進行實物實驗。

6 實驗與分析

6.1 實驗設備

實驗平臺如圖2所示，所采用的視覺定位設備為廣州艾目易的AP-STD-200雙目視覺定位系統,其位置定位精度為0.12 mm，姿態定位精度不詳。機器人設備為UR5協作機器人，具有6個自由度，位置定位精度為0.1 mm，姿態定位精度不詳。手眼標定程序的開發環境為Visual Studio Community2022，采用C++作為編程語言。

圖2 實驗平臺Fig.2 Experimental platform

6.2 實驗方案

et=d1-d2

(25)

er=P(R1)-P(R2)

(26)

式中：et為整體誤差平移部分；d1為機器人控制器讀出的在機器人坐標系下TCP坐標值；d2為雙目視覺計算的TCP坐標轉換到機器人坐標系下的坐標值；er為整體誤差的旋轉部分；R1為機器人控制器讀出的TCP在機器人坐標系下的旋轉矩陣；R2為雙目視覺計算的TCP的旋轉矩陣轉換到機器人坐標系下的旋轉矩陣；P(R)為旋轉矩陣R對應的旋轉矢量。

具體實驗流程如下：

第1步，設置機器人TCP常用刀具工作點(實驗中設置其與視覺識別標志物距離在200 mm左右)。

第4步，移動機器人，根據式(25)與式(26)計算60種不同位姿下的整體誤差，并記錄。

第5步，改變純平移的次數，依次為4、5、6、7、8次，重復第1步到第4步的操作。

按照上述實驗流程，獲取6組數據進行分析。

6.3 數據分析

按照第6.2節的實驗流程進行實驗，整體誤差的實驗結果如表2所示。

表2 實物實驗整體誤差Tab.2 Overall error of physical experiments

7 結論

文中論述了一種無需測量姿態數據的手眼標定算法，進行了仿真實驗和實物實驗，驗證了該算法的有效性，對比了不同純平移采樣點下的標定誤差。在雙目視覺相機位置定位精度0.1 mm、姿態定位精度不詳、機器人定位精度0.1 mm、姿態定位精度不詳的條件下，標定誤差的平移部分在0.411 mm以下，旋轉部分在4.0 mrad以下，能夠滿足大部分口腔手術機器人手眼標定的精度要求。