基于相軌跡的機組阻尼系數(shù)最小二乘量化方法

郭 岐，陸雪頂，王光政

（1.華北水利水電大學(xué)電力學(xué)院，河南 鄭州 450045；2.華中科技大學(xué)土木與水利工程學(xué)院，湖北 武漢 430074）

0 引 言

隨著清潔能源大規(guī)模并網(wǎng)和各區(qū)域電力系統(tǒng)的互聯(lián)，以低頻振蕩為代表的動穩(wěn)定問題日益凸顯。工程表明，超低頻振蕩問題在水電為主導(dǎo)的電力系統(tǒng)中尤為突出，其中以云南電網(wǎng)為典型代表的多個高水電占比電力系統(tǒng)均發(fā)生過超低頻振蕩現(xiàn)象［1-3］。不僅國內(nèi)，美國、土耳其、加拿大等國的電網(wǎng)也出現(xiàn)過超低頻振蕩現(xiàn)象［4-6］。相比低頻振蕩，超低頻振蕩的振蕩頻率更低，其頻率低于0.1 Hz，且影響范圍更廣，振蕩為整個區(qū)域的公共振蕩［7］。

研究電力系統(tǒng)超低頻振蕩廣泛采用的方法有模式分析法和阻尼轉(zhuǎn)矩法［8，9］。其中，模式分析側(cè)重于指導(dǎo)設(shè)計，對振蕩產(chǎn)生機理的解釋不足，而阻尼轉(zhuǎn)矩法物理意義明確，能更好的解釋系統(tǒng)低頻振蕩的機理［10］。文獻［11］指出負阻尼作用是導(dǎo)致系統(tǒng)超低頻范圍不穩(wěn)定的重要成因，并通過分析阻尼對系統(tǒng)參數(shù)敏感性，評估參數(shù)對系統(tǒng)超低頻振蕩的影響程度。文獻［12］設(shè)計了超低頻振蕩附加阻尼控制器，并以阻尼為指標優(yōu)化控制器控制參數(shù)，實現(xiàn)了超低頻振蕩的抑制。此外，許多學(xué)者們以附加阻尼控制為思路，在水輪機調(diào)節(jié)系統(tǒng)控制器參數(shù)的優(yōu)化與相位補償控制器的設(shè)計等方面取得了積極的成果［13-15］。總體而言，阻尼系數(shù)是系統(tǒng)超低頻振蕩分析的重要指標，有效量化機組的阻尼對控制參數(shù)的優(yōu)化與系統(tǒng)的設(shè)計都至關(guān)重要。

傳統(tǒng)的阻尼系數(shù)計算方法利用原動機系統(tǒng)開環(huán)頻率特性進行計算，依賴線性系統(tǒng)傳遞函數(shù)表達式，難以適應(yīng)強非線性系統(tǒng)［16］。因此，研究人員在非線性系統(tǒng)阻尼量化評估上開展了積極的研究。馬騫等提出一種基于超低頻振蕩錄波曲線的阻尼系數(shù)量化方法［17］，通過測量功率、頻率的正弦特征有效地實現(xiàn)實際機組阻尼的快速量化，但計算僅依賴于少量的峰值數(shù)據(jù)，在抗干擾性與評估準確性存在不足，適合系統(tǒng)的在線阻尼評估。劉冬等利用“頻率-功率”相軌跡來量化機組阻尼［18］，利用批量的時域數(shù)據(jù)，整體評價系統(tǒng)的阻尼特性，方法抗干擾性強、準確性高，但量化需要經(jīng)過相圖繪制、軌跡平移和梯度下降尋優(yōu)等步驟，操作復(fù)雜、計算繁瑣，方法適合強非線性系統(tǒng)離線阻尼評估。

綜上所述，現(xiàn)有的阻尼系數(shù)量化方法在對強非線性系統(tǒng)評估時難以兼顧計算準確性與操作簡便性，亟需提出一種能適用于強非線性系統(tǒng)、抗干擾性強且操作簡便的阻尼轉(zhuǎn)矩量化方法。

本文首先分析了超低頻振蕩機組的阻尼特性，利用阻尼轉(zhuǎn)矩理論推導(dǎo)出基于相軌跡最小二乘擬合的機組阻尼量化方法；其次，通過量化值與理論值對比和多機系統(tǒng)超低頻振蕩分析驗證了方法的計算準確性和有效性；最后，利用實際機組的監(jiān)測信號校驗了該量化方法對強非線性系統(tǒng)的適用性。

1 超低頻振蕩機組阻尼分析

1.1 單機系統(tǒng)阻尼特性

原動機調(diào)節(jié)系統(tǒng)一般由調(diào)速器和原動機組成，如圖1所示，Ggov（s）為調(diào)速器線性模型，GH（s）為原動機線性化模型。設(shè)原動機調(diào)節(jié)系統(tǒng)的傳遞函數(shù)為G（s），系統(tǒng)的傳遞函數(shù)模型為：

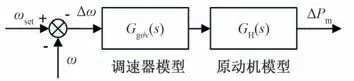
圖1 原動機調(diào)節(jié)系統(tǒng)線性化模型Fig.1 The linearized model of turbine governing systems

式中：G（s）=Ggov（s）GH（s），Δω為轉(zhuǎn)速增量，ΔPm為原動機機械功率增量。

基于Phillips-Heffron模型，將s=jω帶入式（1）得：

式中：Dm為阻尼轉(zhuǎn)矩系數(shù)，是ΔPm在Δω軸的分量；Km為同步轉(zhuǎn)矩系數(shù)，是ΔPm在Δδ軸方向的分量。

ΔPm的分解如圖2所示。

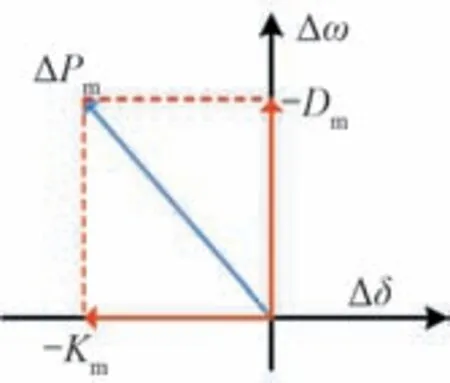
圖2 ΔPm分解示意Fig.2 The decomposition of ΔPm

以水電機組為例，為了便于分析，僅考慮功角變化引起的電磁轉(zhuǎn)矩變化，同步發(fā)電機的二階運動方程為：

式中：Δδ為發(fā)電機功角增量，Δω為發(fā)電機角速度增量，ω0為發(fā)電機同步角速度，ΔPm為發(fā)電機機械功率增量，ΔPe為發(fā)電機電磁功率增量，D為發(fā)電機阻尼系數(shù)，Ta為機組慣性時間常數(shù)。

如果忽略網(wǎng)絡(luò)損失，可近似認為電磁增量等于有功增量即：

式中：ΔPL為發(fā)電機有功增量；KL為負荷頻率調(diào)節(jié)系數(shù)。

將式（2）和式（4）帶入式（3）得：

由式（5）可知系統(tǒng)的阻尼比為：

式中：KL與D為常數(shù)，Dm的大小將影響系統(tǒng)的阻尼特性。

結(jié)合ΔPm分解圖2與式（6）可知Dm的作用十分明確：當Dm＜0 時，-Dm與Δω同向，調(diào)速系統(tǒng)Δω起促進作用，ξ減小，這將加劇系統(tǒng)頻率振蕩。相反，當Dm＞0，-Dm與Δω方向相反，ξ增加，這將抑制系統(tǒng)振蕩。所以，當Dm＜0時，調(diào)速原動系統(tǒng)向系統(tǒng)提供負阻尼，Dm＞0時調(diào)速原動系向系統(tǒng)提供正阻尼。

1.2 多機并列運行頻率調(diào)速系統(tǒng)阻尼特性

為便于分析多機組并列運行情況下原動機調(diào)節(jié)系統(tǒng)，可假設(shè)各并網(wǎng)運行機組保持嚴格的同步運行，即“剛性聯(lián)結(jié)”假設(shè)，此時可以把所有參與頻率調(diào)節(jié)的機組折算為一臺等效機組［19］，如圖3所示。系統(tǒng)機組總功率偏差為：

圖3 “剛性聯(lián)結(jié)”多機運行系統(tǒng)線性化模型方框圖Fig.3 Block diagram of linearization model of the multi-machine operating system with “rigid coupling”

式中：ΔPme為并列機組等效機械功率偏差；i為調(diào)頻機組的編號；ki為i機組額定出力占系統(tǒng)總?cè)萘康谋戎亍?/p>

計算多機系統(tǒng)的阻尼轉(zhuǎn)矩系數(shù)為：

式中：Dme為多機系統(tǒng)原動機提供的等效阻尼轉(zhuǎn)矩系數(shù)；Dmi為i原動機系統(tǒng)提供的阻尼轉(zhuǎn)矩系數(shù)。

與單機分析類似，等效系統(tǒng)的阻尼比為：

式中：ξe為系統(tǒng)的等效阻尼比；KLe為等效同步轉(zhuǎn)矩系數(shù)；KLe為等效系統(tǒng)的等效負荷頻率調(diào)節(jié)系數(shù)；De為等效發(fā)電機阻尼系數(shù)。

由式（8）和式（9）可知，多機原動機系統(tǒng)中各機組向系統(tǒng)提供阻尼轉(zhuǎn)矩系數(shù)滿足線性疊加關(guān)系，系統(tǒng)總的阻尼比與各原動機系統(tǒng)提供的阻尼轉(zhuǎn)矩系數(shù)也是線性關(guān)系。因此，準確量化各調(diào)頻機組的阻尼轉(zhuǎn)矩系數(shù)，對于超低頻振蕩發(fā)生原因的定位與消除十分必要。

2 機組阻尼轉(zhuǎn)矩量化方法

2.1 方法原理

對開環(huán)線性系統(tǒng)給定頻率的正弦輸入，穩(wěn)態(tài)后系統(tǒng)輸出響應(yīng)也為正弦擾動［20］，如圖4所示。對ΔPm∕Δω進行如式（10）的推導(dǎo)。

圖4 線性系統(tǒng)頻率正弦擾動穩(wěn)態(tài)響應(yīng)Fig.4 Steady-state response of linear systems under frequency sine frequency disturbance

式中：ωa為正弦擾動頻率；A為幅頻特性；θ為相頻特性；A和θ分別是關(guān)于ωa的函數(shù)A(ωa)，θ(ωa)。

推導(dǎo)的幾何意義是先將Δω和ΔPm兩個信號映射在Δω-ΔPm相平面中，然后對相軌跡進行求導(dǎo)以求取相軌跡斜率，最后將相軌跡的斜率分解為一個常量Acos(θ(ωa))和周期量sin(ωat)sin(θ)。因此，對于任意確定ωa的正弦擾動響應(yīng)，Δω- ΔPm相軌跡的斜率由固定的斜率Acos(θ(ωa))和隨時間周期變化的f(θ，ωa，t)斜率疊加得到。結(jié)合阻尼系數(shù)表達式即式（2）可知，相軌跡固定的斜率就是阻尼轉(zhuǎn)矩系數(shù)即Dm=Acos(θ(ωa))。因此，相圖上一定可以找到斜率為Dm的唯一直線來表征系統(tǒng)的阻尼系數(shù)，如圖5所示。

圖5 相軌跡斜率組成Fig.5 Composition of the slope of the phase trajectory

對于強非線性系統(tǒng)，無法通過求取開環(huán)傳遞函數(shù)實部的方式獲得阻尼轉(zhuǎn)矩系數(shù)，但是可通過測量∕仿真的方式，得到系統(tǒng)的Δω- ΔPm相軌跡。利用式（10）的相軌跡斜率分解思想，可尋找到唯一的最優(yōu)的直線，直線斜率表征系統(tǒng)的阻尼轉(zhuǎn)矩系數(shù)Dm。由于相軌跡斜率是由固定值和周期值疊加而成，因此可以采用最小二乘法擬合這條最優(yōu)的直線，使得該直線的均方誤差最小，如式（11）所示：

式中：Xi為相圖上第i點的Δωi所對應(yīng)的ΔPm_i值；X′i為直線上第i點的Δωi所對應(yīng)的ΔPm_i值。

2.2 量化流程

依據(jù)最小二乘法量化機組阻尼系數(shù)的原理可寫出阻尼系數(shù)快速量化方法的流程，如圖6所示，詳細流程如下：

圖6 阻尼量化流程Fig.6 Process of the damping quantification method

（1）初始化原動機調(diào)節(jié)系統(tǒng)仿真模型；

（2）輸入固定頻率的正弦頻率擾動負反饋；

（3）對原動機調(diào)節(jié)系統(tǒng)進行時域仿真，并記錄功率信號；

（4）將頻率信號和功率信號轉(zhuǎn)換為偏差相對值；

（5）利用最小二乘法將轉(zhuǎn)換后的頻率信號和功率信號擬合為直線；

（6）輸出直線斜率的相反數(shù)即為原動機系統(tǒng)提供的阻尼轉(zhuǎn)矩系數(shù)。

對于搭建的原動機系統(tǒng)仿真模型，如果沒有振蕩信號，阻尼量化流程為（1）～（6）；如果能夠直接采集到頻率和功率信號，便可跳過開環(huán)系統(tǒng)正弦頻率擾動仿真，直接擬合直線便可得到阻尼，其步驟為（4）～（6）。

3 算例分析

本部分將利用單機模型、多機模型以及實際系統(tǒng)的實測數(shù)據(jù)來驗證基于相軌跡最小二乘擬合阻尼量化方法的準確性、有效性與適用性。

3.1 算例1：單機系統(tǒng)阻尼量化分析

為了驗證該量化方法的精度，以簡化的理想水輪機調(diào)速系統(tǒng)模型為對象，如圖7所示。將量化的阻尼系數(shù)和機組阻尼系數(shù)的理論值進行對比，以計算0.01～2.5 Hz頻率范圍內(nèi)對應(yīng)阻尼系數(shù)為例，頻率計算步長設(shè)置為0.01 Hz，重復(fù)給定不同頻率的正弦頻率擾動信號，計算各振蕩頻率下的阻尼系數(shù)，阻尼系數(shù)的理論值由開環(huán)系統(tǒng)的幅頻特性計算得到。理論值與量化值對比如圖8所示。

圖7 簡化水輪機調(diào)節(jié)系統(tǒng)Fig.7 Simplified hydro-turbine regulation systems

由圖8可知，基于相圖的阻尼系數(shù)最小二乘量化方法得到的阻尼量化值曲線與阻尼理論值曲線十分契合，誤差維持在10-4左右，這表明方法能準確計算出機組的阻尼轉(zhuǎn)矩系數(shù)。

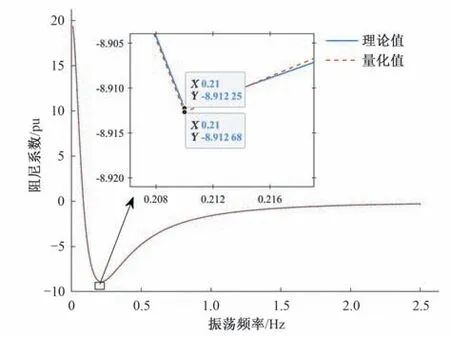
圖8 最小二乘量化的阻尼與理論阻尼的對比（K=20，Tv=2，Tw =1）Fig.8 Comparison of quantified damping values with theoretical damping values （K=20，Tv=2，Tw =1）

3.2 算例2：4機系統(tǒng)阻尼量化分析

為了進一步分析方法在多機系統(tǒng)中的有效性，基于MATLAB∕Simulink2020b 建立了一個高水電占比的4 機并列運行系統(tǒng)，如圖9所示。其中，1～2號為同型火電機組，3～4號機組為同型水電機組，所有機組的額定容量均為700 MW，機組初始運行在額定工況。

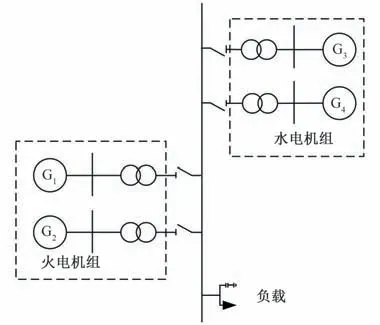
圖9 4機并列運行系統(tǒng)Fig.9 Four-machine parallel operating systems

1～3 號機組控制參數(shù)設(shè)計為實際值，通過改變4 號機組調(diào)速器參數(shù)將其設(shè)置為負阻尼機組，并使系統(tǒng)處于臨界穩(wěn)定狀態(tài)。在0.1 s 時，對系統(tǒng)施加+1%的負載擾動，系統(tǒng)產(chǎn)生了頻率約0.05 Hz 的超低頻振蕩，在87.5 s 時對4 號機組設(shè)置人工死區(qū)使其退出調(diào)頻，系統(tǒng)恢復(fù)穩(wěn)定。利用0～80 s 內(nèi)1～4 號機組的頻率和功率信號，分別對各機組的“功率-頻率”信號進行最小二乘量化。系統(tǒng)的頻率響應(yīng)與各機組的阻尼量化如圖10所示。

由圖10可知，1～3 號機組“頻率-功率”相軌跡向下傾斜，均向系統(tǒng)提供正阻尼；而4號機組相軌跡向上傾斜，阻尼轉(zhuǎn)矩系數(shù)為-0.997 2，其在振蕩的過程中向系統(tǒng)提供負阻尼。從阻尼轉(zhuǎn)矩系數(shù)的角度分析，4號為系統(tǒng)超低頻振蕩的誘發(fā)機組。因此，在87.5 s 時退出4 號組的調(diào)頻，系統(tǒng)便可恢復(fù)穩(wěn)定。進一步，將四臺機組量化的阻尼系數(shù)進行線性疊加，計算系統(tǒng)的等效阻尼系數(shù)Dme=-0.030 9，結(jié)合仿真系統(tǒng)中KL=0.03，D=0，k1=k2=k3=k4=0.25 的設(shè)置信息，由式（9）可以計算出系統(tǒng)的阻尼比ξe=-0.000 9，所以系統(tǒng)基本處于臨界穩(wěn)定狀態(tài)。主導(dǎo)機組的定位驗證與阻尼比的驗算均表明所提方法在多機系統(tǒng)中應(yīng)用十分有效。

圖10 4機并列運行系統(tǒng)仿真與阻尼量化Fig.10 Simulation and damping quantification of the 4-machine parallel operation systems

3.3 算例3：實際系統(tǒng)超低頻振蕩阻尼量化分析

為了驗證方法在強非線性系統(tǒng)中的適用性，此部分采用云南電網(wǎng)異步并網(wǎng)小擾動實驗時超低頻振蕩實測數(shù)據(jù)，對某火電站與某水電站的機組阻尼進行量化。其中機組的基本計算參數(shù)如表1所示。水電、火電機組的“頻率-功率”實測信號與阻尼轉(zhuǎn)矩系數(shù)的量化結(jié)果如圖11所示。

表1 機組計算參數(shù)Tab.1 Calculated parameters of units

由圖11可知，水電機組“頻率-功率”相軌跡明顯向上傾斜，量化的阻尼轉(zhuǎn)矩系數(shù)為-7.365 8。工程中如果機組阻尼系數(shù)低于-1，便可認為該機組是超低頻主導(dǎo)機組［17］。因此，該水電機組在實際的系統(tǒng)振蕩過程中提供強負阻尼，是超低頻振蕩的主導(dǎo)機組之一。同時，由圖11（b）可知，火電機組在振蕩過程中向系統(tǒng)提供了強正阻尼。整體而言，由于系統(tǒng)火電比例較低而水電比例較高，火電的強正阻尼效應(yīng)大部分被水電負阻尼效應(yīng)抵消，因此系統(tǒng)容易產(chǎn)生超低頻振蕩，這也是云南電網(wǎng)易發(fā)生超低頻振蕩的內(nèi)在原因。所以，當電網(wǎng)將與該水電機組類似的12臺強負阻尼水電機組退出一次調(diào)頻后，系統(tǒng)的低頻振蕩得以消除。因此，基于相軌跡的阻尼最小二乘量化方法在實際的強非線性系統(tǒng)的分析中也同樣適用。

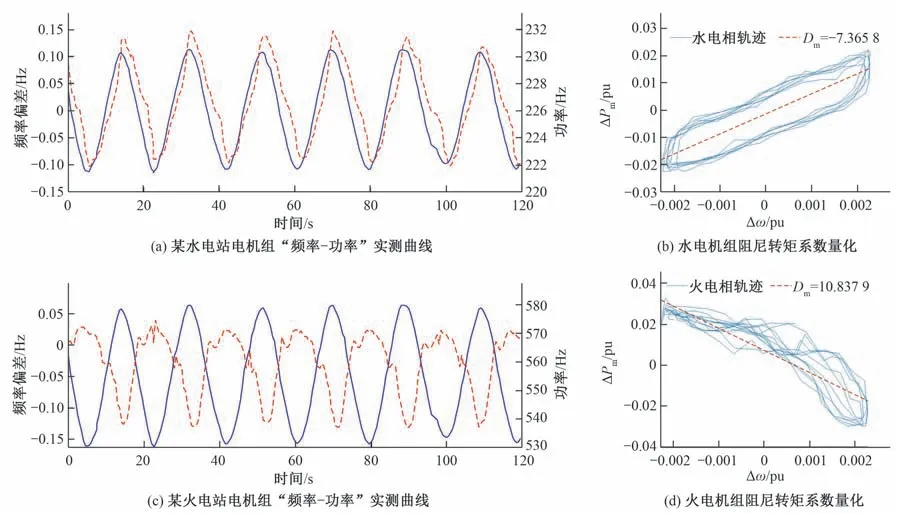
圖11 超低頻振蕩實際機組曲線與阻尼量化Fig.11 Ultra-low frequency oscillation actual unit curve and damping quantification

4 結(jié) 論

本文提供了一種原動機系統(tǒng)阻尼轉(zhuǎn)矩系數(shù)量化的一般方法，包括相平面映射與最小二乘擬合。經(jīng)過系列的理論推導(dǎo)與案例計算可得到如下結(jié)論。

（1）方法由嚴格的理論推導(dǎo)得出，操作簡單，量化的結(jié)果符合阻尼轉(zhuǎn)矩系數(shù)的理論定義。

（2）方法的計算精度較高，線性系統(tǒng)量化出的阻尼系數(shù)與理論阻尼系數(shù)的誤差可維持在10-4左右。

（3）通過4機系統(tǒng)案例與實測系統(tǒng)案例的驗算，方法能有效量化多機系統(tǒng)和復(fù)雜非線性系統(tǒng)的阻尼轉(zhuǎn)矩系數(shù)。方法可為實際電力系統(tǒng)中振蕩機組的在線監(jiān)測與復(fù)雜非線性系統(tǒng)的阻尼分析提供有效的技術(shù)與理論支持。在后續(xù)的工作中，將該方法應(yīng)用在分析系統(tǒng)阻尼對各類非線性因素敏感性上將會是一個重要的研究方向。