基于BP神經網絡的車輛跟馳模型研究*

王天方 ， 劉學淵 ，2

（1.西南林業大學機械與交通學院，云南 昆明 650224；2.云南省高校高原山區機動車環保與安全重點實驗室，云南 昆明 650224）

0 引言

隨著人們生活水平和購買力的不斷提高，每個家庭擁有一輛車似乎已經成為一種標配，因此，我國的機動車保有量每年都在大幅增加。然而，汽車在改善人們生活品質的同時，也會帶來相應的交通問題和環境問題。機動車保有量的逐年增加，給有限的道路交通資源帶來了極大的壓力，導致交通事故頻發、道路擁擠等一系列交通問題。特別是在早晚上下班這個特殊時間段，堵車已經成為一種常態化現象。除了交通問題，機動車尾氣排放也對環境造成了嚴重的破壞，主要原因是汽車排放物是污染物的一個主要來源。《中國移動源環境管理年報（2021）》[1]顯示，2020年，全國機動車四項污染物排放總量達到了1 593萬t。無論是交通問題還是排放污染問題都與人們息息相關，如何應對這些問題已成為社會各界關注的焦點。

跟馳行為是城市交通中常見的車輛行駛狀態，其特性對交通和環境有重要影響，所以對車輛跟馳行為的研究，對解決交通問題和排放問題具有很重要的現實意義。早在1950年，人們就開始對跟馳行為進行研究，并提出了一系列模型，如刺激-反應模型[2-3]、安全距離模型[4-5]、心理-生理學模型[6-7]等。雖然這些模型能夠很好地模擬跟馳場景，但是這些模型都是建立在準確的數學公式之上，所以傳統的跟馳模型在實際應用中會受到很大的限制。隨著科學技術的發展，能夠獲取的跟馳數據更多，并且精度更高，使得數據驅動類跟馳模型[8]的研究在近年來得到了一定發展，而且很多學者都對其進行過相關的研究。例如，Zhou等[9]提出了一種基于遞歸神經網絡的跟馳模型，該模型能夠預測和捕捉交通震蕩。孫倩等[10]提出了一種基于長短期記憶神經網絡的跟馳模型，基于該模型進行交通仿真并研究駕駛員的記憶效應影響因素。蔣華濤等[11]將最小安全距離模型與灰色神經網絡結合，提出了灰色神經網絡跟馳模型，該模型能夠提前預知前車未來車速和制動跡象。Hao等[12]提出了一種不包含數學分析的人工智能跟馳模型，該模型能夠精準地模仿人類駕駛員。

在智能化技術高度發展的今天，將跟馳行為融入智能化輔助駕駛系統，對于減輕人們的駕駛壓力并保障交通安全有重要意義。實現這一過程需要準確的數學模型來支撐，但是，在實際駕駛過程中駕駛員受到的影響因素并不唯一，如駕駛員經常會同時受到交通信號、其他車輛和行人的影響。對于這種比較復雜的情況，不能用單一的數學模型進行建模，要使用人工神經網絡等方法來描述。因此，課題組以實際采集的實驗數據為基礎，建立BP神經網絡跟馳模型。

1 實驗過程與數據采集

在本次實驗過程中，使用兩臺實驗車輛，一輛作為前導車，一輛作為跟馳車，在前、后車輛上都安裝全球定位系統（Global Positioning System, GPS），然后通過實驗設備獲取實際道路車輛的跟馳行為數據。實驗道路為昆明市的北京路。選擇的實驗路段為主干道，整體車流量較大，在實驗過程中，為了保證跟馳的真實性，駕駛員將會按照自己在日常生活中的駕駛習慣正常駕駛實驗車輛。跟馳行為數據主要由GPS獲取，GPS可以獲取車輛速度、經緯度、海拔等數據。

2 建立跟馳模型

以實際跟馳行為數據為基礎，選取一個典型且連續的跟車過程，運用BP神經網絡構建跟馳模型。在進行BP神經網絡的設計時，首先需要一個樣本訓練數據集，然后確定模型的輸入輸出參數。將實際道路采集到的跟馳行為數據作為訓練樣本，然后根據獲取的數據提取前車車速V1（km/h）、相對距離Rs（m）、前車對后車的相對速度RV（km/h）和后車車速V2（km/h）作為輸入，后車下一時刻的速度V(t+1)（km/h）作為輸出。輸入、輸出確定之后，需要從以下幾個方面對神經網絡結構進行設計。

2.1 網絡層數

BP神經網絡的層數設計可以根據自己的需求而定，一般單層的網絡就可以滿足大部分的應用，因為只需要增加神經元節的個數就可以完成任意的非線性映射。但是，樣本的數量較多時，可以選擇增加一個隱含層，能夠減少網絡規模并提高輸出精度。所以，本文將建立雙隱含層的BP神經網絡跟馳模型。

2.2 輸入和輸出層節點數

對于BP神經網絡而言，輸入層神經元節點數一般為輸入參數的個數，因為本文選擇的輸入參數有4個，所以輸入層的神經元個數為4。輸出層節點數和輸入層類似，根據輸出參數個數確定，因此輸出層的神經元個數為1。

2.3 隱含層節點數

隱含層節點數一般是根據試湊法得出選取范圍，然后根據訓練時不同神經元對模型的影響，選出最佳個數。確定神經元個數的主要公式如下：

式中：n為輸入層神經元個數，m為輸出層神經元個數，M為隱含層神經元個數，a為[0,10]之間的常數。公式（1）是比較常用的經驗公式，第一隱含層根據試湊法確定神經元個數為6；第二隱含層神經元個數等于輸出節點數時，模型的預測效果較好[13]，因此第二隱含層神經元個數設置為1。BP神經網絡跟馳模型的結構為4-6-1-1。

2.4 傳遞函數和學習算法

BP神經網絡的傳遞函數可以使用線性函數或Sigmoid函數，文中隱含層的傳遞函數選擇Sigmoid函數，輸出層選擇線性函數，因為如果輸出層選用Sigmoid函數會限制輸出數值的范圍。

標準的BP網絡使用的學習算法是最速下降法，也稱為梯度下降法，采用最速下降法對網絡的權值進行調整的過程，是一個沿著網絡逐層反向調整的過程，具體為先對輸出層和隱含層的權值進行調整，然后再對隱含層與輸入層之間的權值進行調整。在實際使用最速下降法訓練的過程中，會存在收斂速度慢的問題，針對最速下降法的這個缺點，提出了LM（Levenberg Marquardt）算法。LM算法是在最速下降法的基礎上改進而來的，同時具有擬牛頓法的局部收斂特性和最速下降法全局特性，因此在本次建模過程中，選用LM算法作為學習算法。LM算法調整網絡權值的公式為：

式中，J是雅克比矩陣，I是單位矩陣，μ是比例系數，且μ＞0。

在確定了上述參數之后，將需要訓練的數據進行歸一化處理，然后輸入模型中進行學習和訓練。

3 跟馳模型的優化

利用遺傳算法（Genetic Algorithm, GA）來優化BP神經網絡，即優化神經的初始權值和閾值，可以避免BP神經網絡在訓練時容易陷入局部最優的缺點，同時提高網絡對樣本的預測能力。許多研究者都使用了遺傳算法優化BP神經網絡，如郭艷君等[14]利用遺傳算法優化BP神經網絡跟車模型，表明GA在優化神經的初始權值和閾值方面有較好的效果；王志紅等[15]利用GA優化BP神經網絡排放預測模型，也取得了較好的預測效果。GA的具體操作步驟如下。

1）初始化種群[16]，種群規模為40。采用浮點編碼對個體進行編碼，因為浮點編碼能夠解決二進制編碼中編碼串過長的問題，計算得到編碼長度為38，計算公式如下：

式中，n為輸入層神經元個數，m為輸出層神經元個數，M1和M2分別為第一、第二隱含層神經元個數。

2）適應度函數。適應度函數表示預測輸出與期望輸出之間的誤差絕對值，公式如下：

式中，yi為i節點的期望輸出，xi為i節點的預測輸出，n1為節點數，a為系數。

3）選擇操作。本文使用經典的輪盤賭法，根據個體適應度大小，對個體進行選擇操作，每一個個體被選擇的概率計算公式如下：

式中，fi為個體i的適應度值，m1為種群中個體總數。

4）交叉。從選擇好的個體中對其進行基因互換，即交叉操作，產生下一代。交叉概率控制著個體之間發生交叉概率的大小。一般交叉概率為0.4～1，本文設定的交叉概率為0.8。

5）變異。對交叉之后的個體以一定的概率使其發生變異，從而產生新的個體。其中，變異概率決定變異發生的可能性，變異概率一般為0.001～0.1。本文設定的變異概率為0.02。

6）當算法運行結果達到最大的精度要求或者最大的迭代次數時，結束遺傳算法操作過程，然后需要把優化好的權值和閾值帶入BP神經網絡進行訓練[17]。

4 模型結果分析

4.1 評價指標

以標準均方根誤差（NRMSE），平均絕對百分誤差（MAPE）和決定系數（R2）作為評價指標。NRMSE反映了模型輸出值與實際值之間的差異性；MAPE是衡量預測模型精度的一個重要指標；R2代表模型的非線性擬合性和預測精度。計算公式如下：

式中，yi表示實驗值，表示模型輸出值，表示實驗值的平均值，N為測試集樣本數量。

4.2 模型結果

將從實驗中采集到的數據分別輸入到上述建立的BP神經網絡和遺傳算法優化后的BP神經網絡跟馳模型中進行訓練和預測，結果分別如圖1和圖2所示。

圖1 BP神經網絡模型

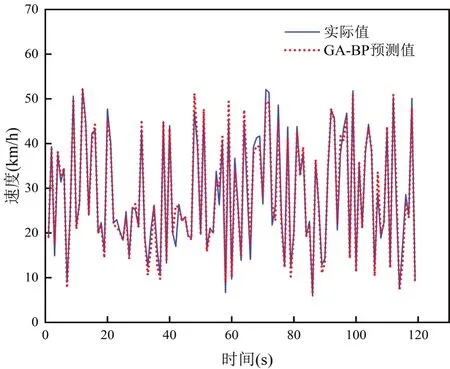
圖2 GA-BP神經網絡模型

從圖1和圖2中可以看到，BP神經網絡模型和GA-BP神經網絡模型的預測值基本都能捕獲實際值的變化趨勢，雖然在圖中可以發現極值點部分預測可能相對較差，但是整體趨勢預測依然準確。對比BP神經網絡模型和GA-BP神經網絡模型，從圖中可以明顯看到GA-BP神經網絡模型具有更好的預測性能，預測值與實際值的誤差也相對較小。由此可見，利用遺傳算法對BP神經網絡的權值和閾值進行優化，能夠使模型達到更好的預測效果[18-19]。

為了進一步分析模型預測偏差，根據模型預測的結果計算模型性能的評價指標值，具體結果如表1所示。從表中可以看到GA-BP神經網絡的評價指標NRMSE、MAPE和R2都優于BP神經網絡模型，具體為NRMSE和MAPE分別降低了20.83%、37.83%，R2提高了3.16%，表明GA優化了BP神經網絡的效果。

表1 模型性能評價指標

4.3 模型誤差分析

為了對模型的預測偏差進行分析，把實際值減預測值定義為模型的誤差。在實驗中，用實際值減去BP神經網絡模型和GA-BP神經網絡模型的預測值，結果如圖3所示。

從圖3中可以看到，GA-BP神經網絡模型相比BP神經網絡模型，誤差更加集中分布在零誤差線左右，偏移相對較小。由此可知，建立的GA-BP神經網絡模型比BP神經網絡模型擁有更好的泛化能力和預測性能，能較好地對跟馳行為進行預測。

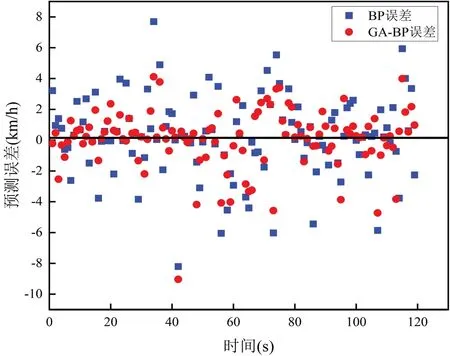
圖3 預測誤差對比

5 總結

課題組以真車實驗采集到的數據為基礎，先使用BP神經網絡構建跟馳模型，然后再使用GA對BP神經網絡跟馳模型進行優化，結果表明，構建的GA-BP神經網絡模型性能的評價指標、預測誤差都要優于BP神經網絡跟馳模型。所以，利用GA優化BP神經網絡模型，能夠有效地提高BP神經網絡跟馳模型預測結果的準確率。