BDS精密鐘差短期預報

王建敏，畢祥鑫，黃佳鵬

BDS精密鐘差短期預報

王建敏，畢祥鑫，黃佳鵬

（遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000）

針對傳統單一預報模型在鐘差預報中誤差積累隨時間的增加而增大問題，提出一種灰度模型GM（1,1）與長短時記憶神經網絡模型（LSTM）的組合模型：采用武漢大學國際全球衛星導航系統服務組織（IGS）數據中心下載的北斗衛星導航系統（BDS）3種軌道不同衛星連續2 d的精密鐘差數據進行建模，首先用GM（1,1）模型進行預報，然后將GM（1,1）模型的殘差利用LSTM神經網絡模型進行再次預報；將2種模型的預報結果進行重構，得到最終的預報結果。實驗結果表明：GM（1,1）/LSTM組合模型與單一GM（1,1）模型相比，精度提高了60%～89%；GM（1,1）/LSTM組合模型與單一LSTM神經網絡相比，精度提升了30%～88%。

鐘差預報；灰度模型（GM（1,1））；長短時記憶神經網絡模型（LSTM）；組合模型

0 引言

自2000年10月31日至今，我國獨立研發的北斗衛星導航系統（BeiDou navigation satellite system，BDS）已經成功發射共55顆3種不同軌道的衛星，將全天候的實時定位導航信息提供給各自的服務對象和地區[1]。目前為止，世界上已經有4個國家和地區建立了自己的全球衛星導航系統（global navigation satellite system, GNSS），分別是美國的全球定位系統（global positioning system,GPS），歐盟的伽利略衛星導航系統（Galileo navigation satellite system, Galileo），俄羅斯的格洛納斯衛星導航系統（global navigation satellite system, GLONASS）以及中國的BDS[2-3]。鐘差是影響衛星定位的重要因素之一，因此，提升鐘差預報的準確性是廣大學者研究的重點和難點。

常見的鐘差預報模型有二次項模型、人工神經網絡模型、自回歸模型、卡爾曼濾波模型等[3-6]。為了得到高精密的預報衛星鐘差，大量的學者對鐘差預報的模型進行了研究。許多學者在鐘差預報方面取得到豐碩的成果。文獻[7]將灰度模型（gray model，GM（1, 1））與修正指數曲線模型（modified exponential curve method, MECM）進行組合，削弱了殘差中的誤差，使其精度比傳統模型的精度有了大幅度提高。文獻[8]采用經典定權的方法將GM(1, 1)和自回歸模型（adaptive resonance, AR）模型進行線性組合，并且對北斗三號全球衛星導航系統（BeiDou-3 navigation satellite system, BDS-3）進行預報，將鐘差數據短期預報的精度提升大約9%～20%。文獻[9]通過求和自回歸平均模型（autoregressive integrated moving average, ARIMA）對鐘差數據進行短期預報，預報結果的精度有了一定的提升。文獻[10]通過粒子群算法來選取灰色神經網絡最優的權值和閾值，提升灰色神精網絡模型預報的精度。文獻[11]通過自適應共振理論（adaptive resonance theory, ART）來構造極端學習機（extreme learning machine, ELM），將ART的聚類體征應用到ELM中，增加極端學習機對鐘差預報的準確性。以上的方法在一定程度上都對鐘差預報模型進行了優化和改進，但是仍存在預報模型在精密鐘差預報過程中殘差的累積，且預報模型在改進的過程中使模型逐漸復雜化，建模的時間增長。

由于GM（1，1）模型具有建模速度快、模型簡單等優點，使模型能更好地實現優化以及和其他模型進行組合[12-14]。因此，本文在諸多學者研究的基礎上提出一種基于擬合殘差法的GM（1,1）灰度模型與長短時記憶神經網絡模型（long-short term mermory network，LSTM）的組合模型。本文采用BDS 3種不同軌道上各2顆衛星的精密鐘差數據進行實驗，通過對比驗證組合模型的有效性和可行性。

1 數據預處理

一般情況下，衛星鐘差的初始數據隸屬于相位數據，而粗差通常隱藏在鐘差數據中且不容易被探測出來，但是在頻率數據集中會被放大[15-16]；因此需要對鐘差數據先進行處理。由于粗差探測需要在相位數據所對應的頻率下進行，因此需要先求出對應相位的頻率。衛星鐘差相位數據和頻率數據的對應關系為

式中：為第i個歷元所對應的相位數據；為i+1歷元所對應的相位數據；為第i個歷元所對應的相位數據的頻率；為相鄰歷元的采樣間隔。為了對比不同衛星數據的差異，在BDS的3種軌道上各選1顆衛星作為結果進行展示。實驗的數據為采樣時間間隔為5 min的2021-11-11—2021-11-12的鐘差數據。選取C02衛星、C08衛星、C14衛星作為實驗所用衛星。實驗衛星對應的相位數據和頻率數據如圖1～圖3所示。

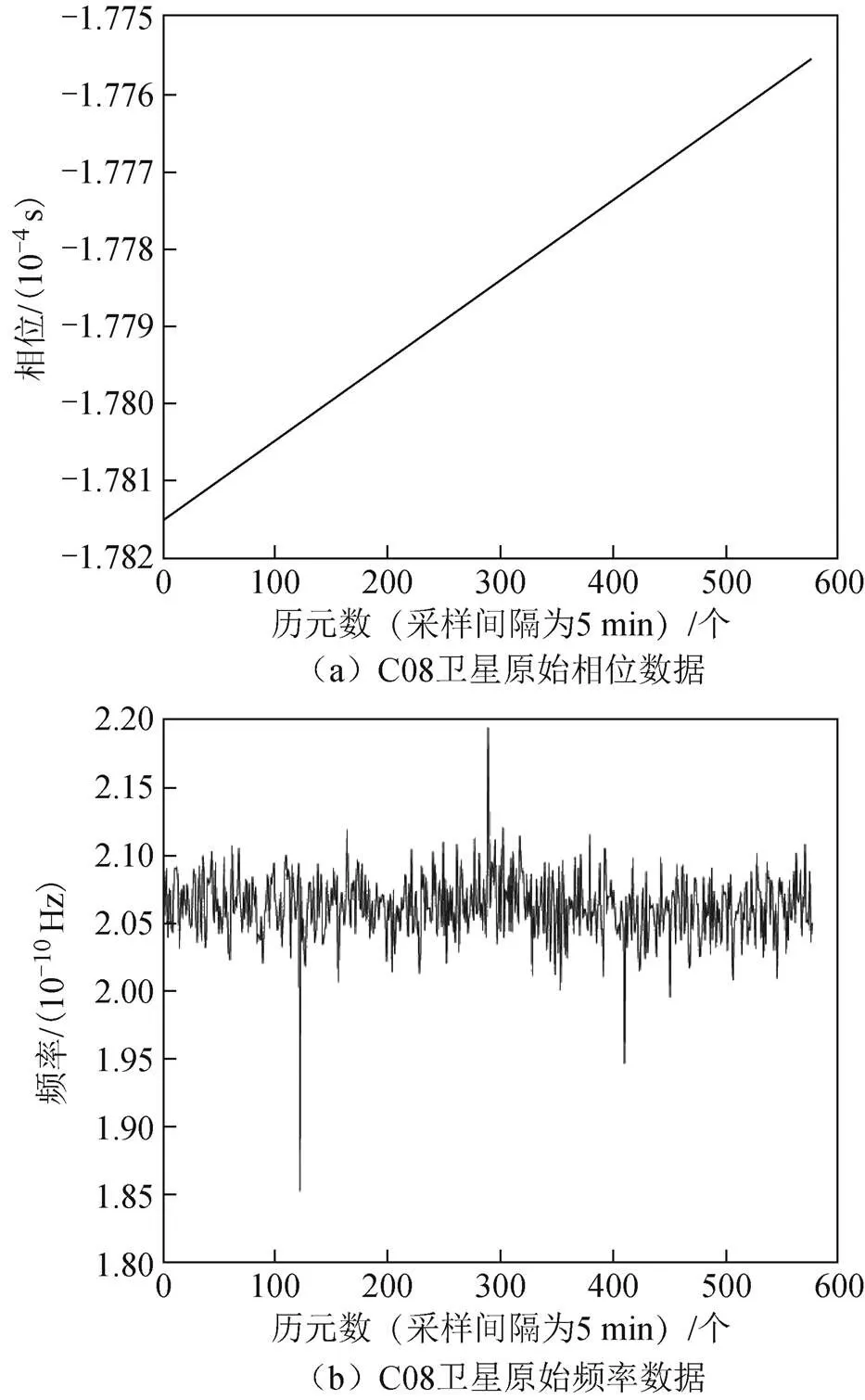
圖2 C08衛星數據

圖3 C14衛星數據

從圖1～圖3中可知：在原始相位數據中，衛星的鐘差序列為線性序列，在這段時間內沒有顯著的跳變誤差；而在原始頻率數據中，頻率數據的平滑性差并且有極值出現。為了預報結果的準確性，需要對原始數據進行粗差剔除。

采用中位數粗差探測法對原始數進行粗差檢測，其公式如下：

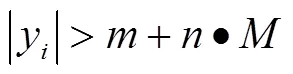
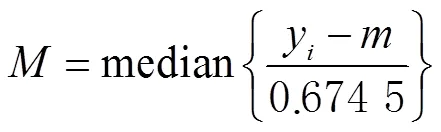
由式（2）、式（3）可知，頻率數據和序列中位數的倍與中位數的和比較，當頻率的數據小時，為正常數據，反之則為粗差數據。將粗差數據剔除，通過線性內插將數據補齊，可得到最終的數據[17-18]。改正后的頻率數據如圖4～圖6所示。

圖4 C02衛星處理后的頻率數據

圖5 C08衛星處理后的頻率數據

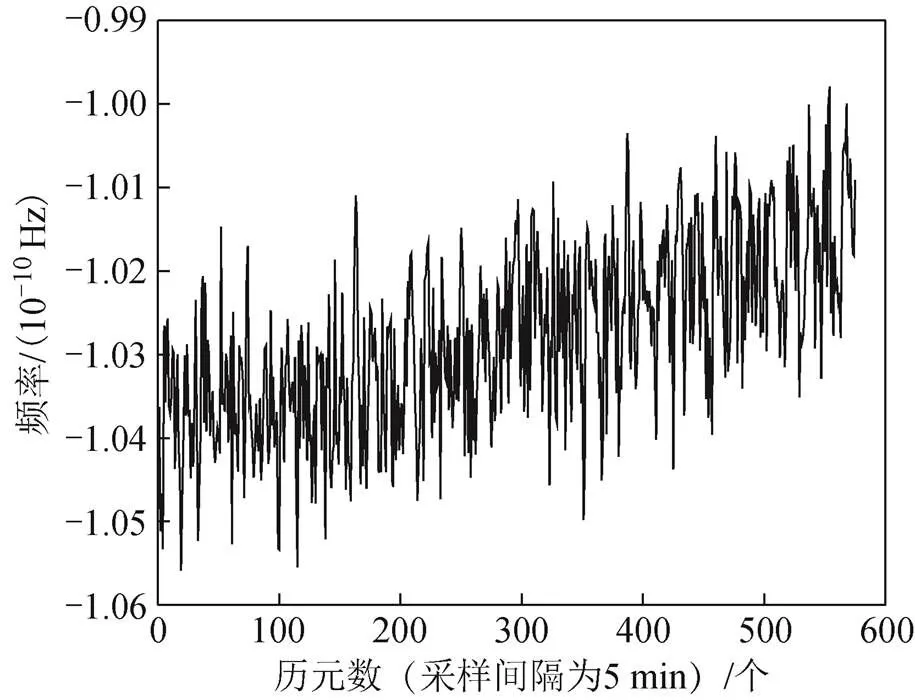
圖6 C14衛星處理后的頻率數據

2 鐘差預報模型

2.1 GM(1,1)模型的建立

灰色模型對于信息不完整、數據量少、雜亂的時間序列進行建模與分析，能夠揭示因素的未來變化趨勢。一階微分灰色預報模型將序列建成微分、差分、近似指數律兼容的模型[19]。GM(1,1)的計算方法如下：

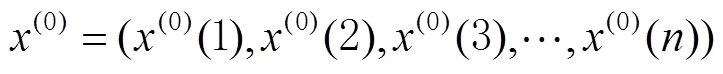
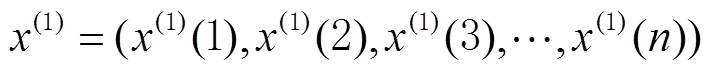
其中

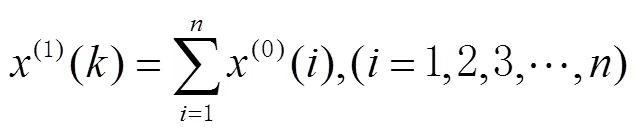
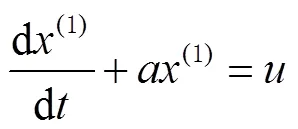
式中：為發展系數；為灰作用量。

4）離散化的矩陣方程為

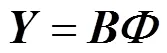
5）利用最小二乘求解，可得

6）將式（9）帶入式（7）可得到白化方程的解為

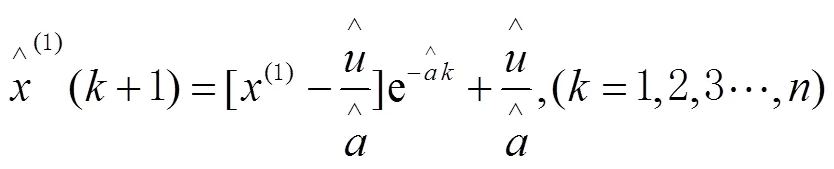
式中e為自然常數。因為模型追求規律性，鐘差數據無法從中提取出來，所以要對其進行遞減還原處理，以得到原數據，其表達式為：

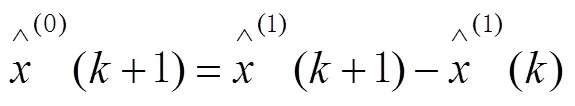
2.2 LSTM神經網絡的建立

近幾年來，在衛星鐘差預報中廣泛應用神經網絡模型，而傳統的神經網絡不會關注前一個時刻的處理會有什么信息能夠應用于下一時刻，每一次都是只關注當前時刻的處理，因此在應用方面會有一些局限性，遞回歸神經網絡（recurrent neural networks，RNNs）可以很好地解決這個問題，它帶有一個指向自身的環，用來表示有哪些前一時刻處理的信息可以應用于下一時刻。但是在數據量大的情況下，RNNs容易出現梯度消失的問題，以至于無法進行長期學習。而LSTM因為有眾多參數，可以避免梯度消失的問題[20]，從而能夠進行長時間的學習。

LSTM的簡單流程如圖7所示。

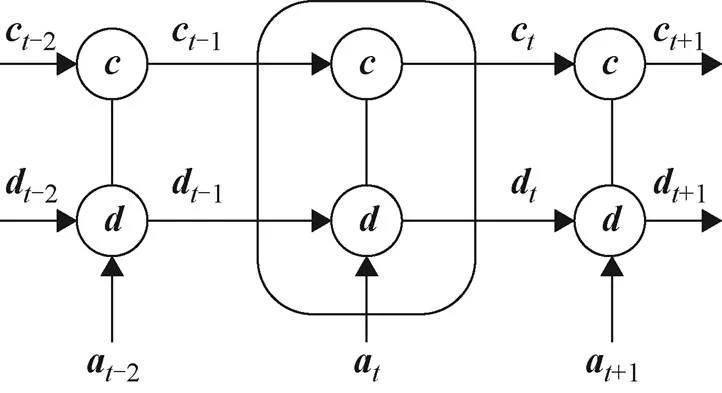
圖7 LSTM流程示意

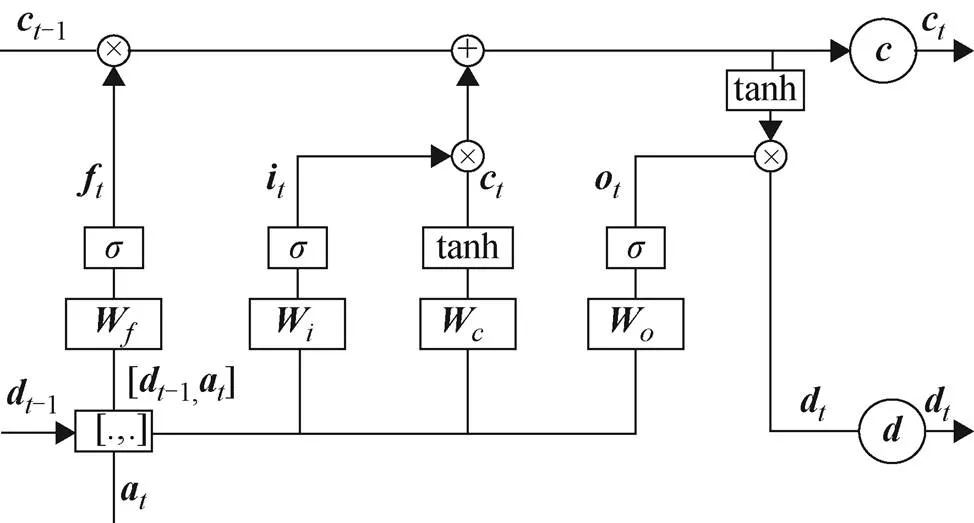
圖8 LSTM單元內部結構

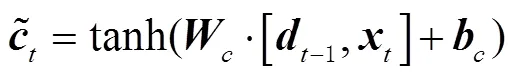
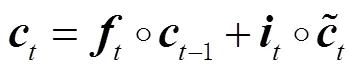
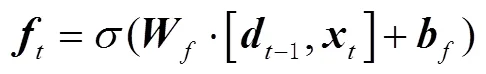
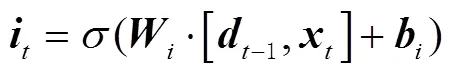
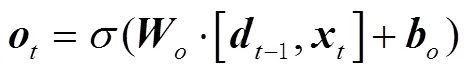
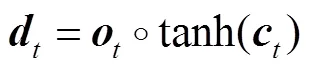
2.3 組合模型

由于GM（1,1）模型和LSTM神經網絡都存在著誤差累積的現象，為了使預報效果更加準確，本文提出一種基于擬合殘差法的GM（1,1）模型與LSTM神經網絡模型組合的BDS衛星鐘差預報的方法。該方法將GM（1,1）模型的殘差序列利用LSTM神經網絡進行建模預報，能夠降低預報模型的誤差累積，提升模型對精密鐘差數據預報的準確性。組合模型的預報基本流程如圖9所示。圖中MAD表示頻率序列偏差的絕對值中位數（median of absolute value）。

3 實驗與結果分析

3.1 數據來源

為了對比GM（1, 1）模型、LSTM神經網絡模型和GM（1, 1）/LSTM組合模型對衛星鐘差數據預報的效果，本次實驗采用從由武漢大學國際GNSS服務數據中心（International GNSS Service，IGS）下載的2021-11-11—2021-11-12共2 d鐘差數據作為對比實驗的建模數據。為了避免實驗的偶然性，在BDS衛星3種軌道上各隨機選取2顆衛星作為進行鐘差預報實驗的衛星，分別為：地球靜止軌道（geostationary orbit，GEO）衛星C02、C03；中圓地球軌道（medium Earth orbit，MEO）衛星C12、C14；傾斜地球同步軌道（inclined geo-synchronization orbit，IGSO）衛星C08、C16。

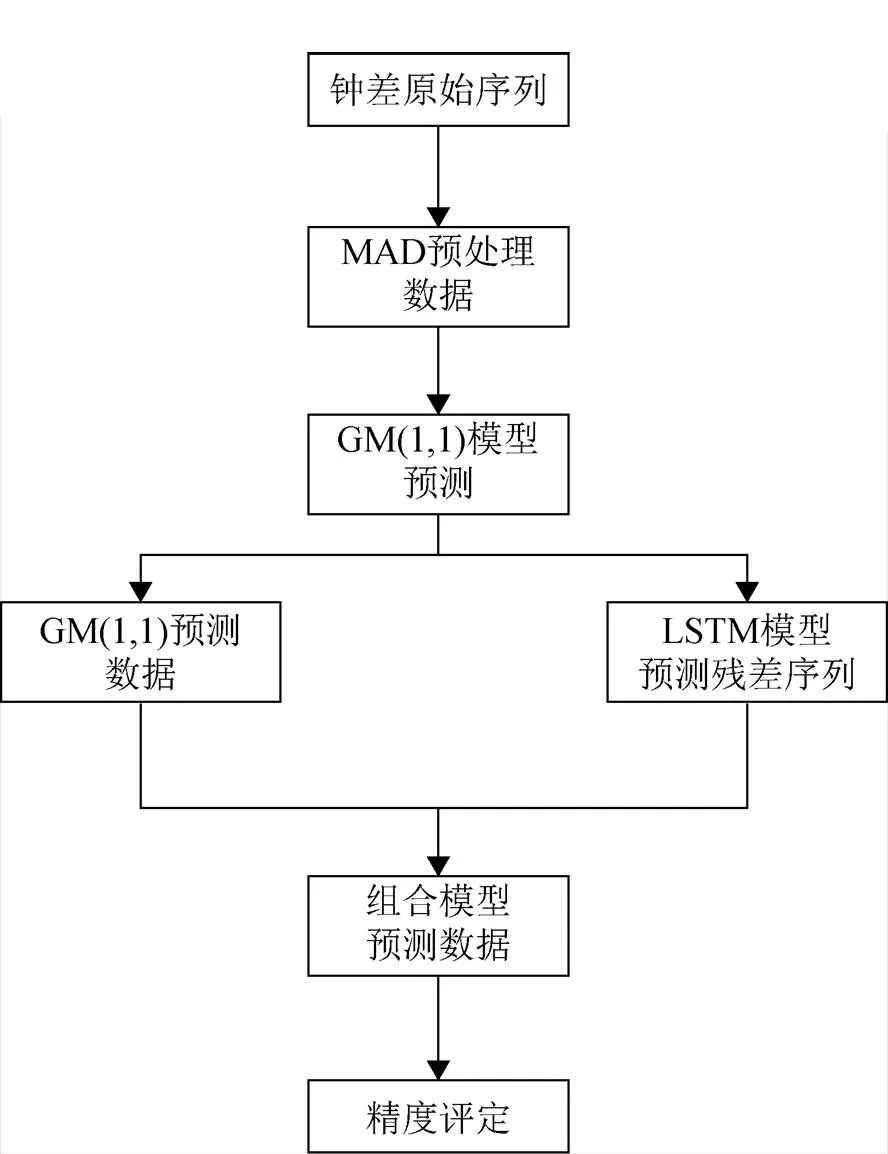
圖9 組合模型預報流程

3.2 方案設計

1）方案一：對C02、C03衛星分別選用GM（1,1）模型、LSTM神經網絡和GM（1,1）/LSTM模型，用24 h的鐘差數據進行建模，來預測未來6、12、18和24 h的鐘差數據。

2）方案二：對C12、C14衛星分別選用GM（1,1）模型、LSTM神經網絡和GM（1,1）/LSTM模型，用24 h的鐘差數據進行建模，來預測未來6、12、18和24 h的鐘差數據。

3）方案三：對C08、C16衛星分別采用GM（1,1）模型、LSTM神經網絡和GM（1,1）/LSTM模型，用24 h的鐘差數據進行建模，來預測未來6、12、18和24 h的鐘差數據。

3.3 結果分析

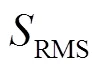
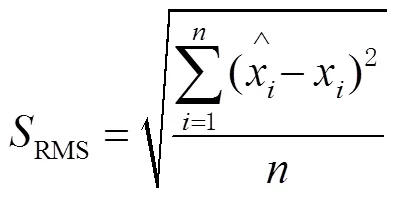
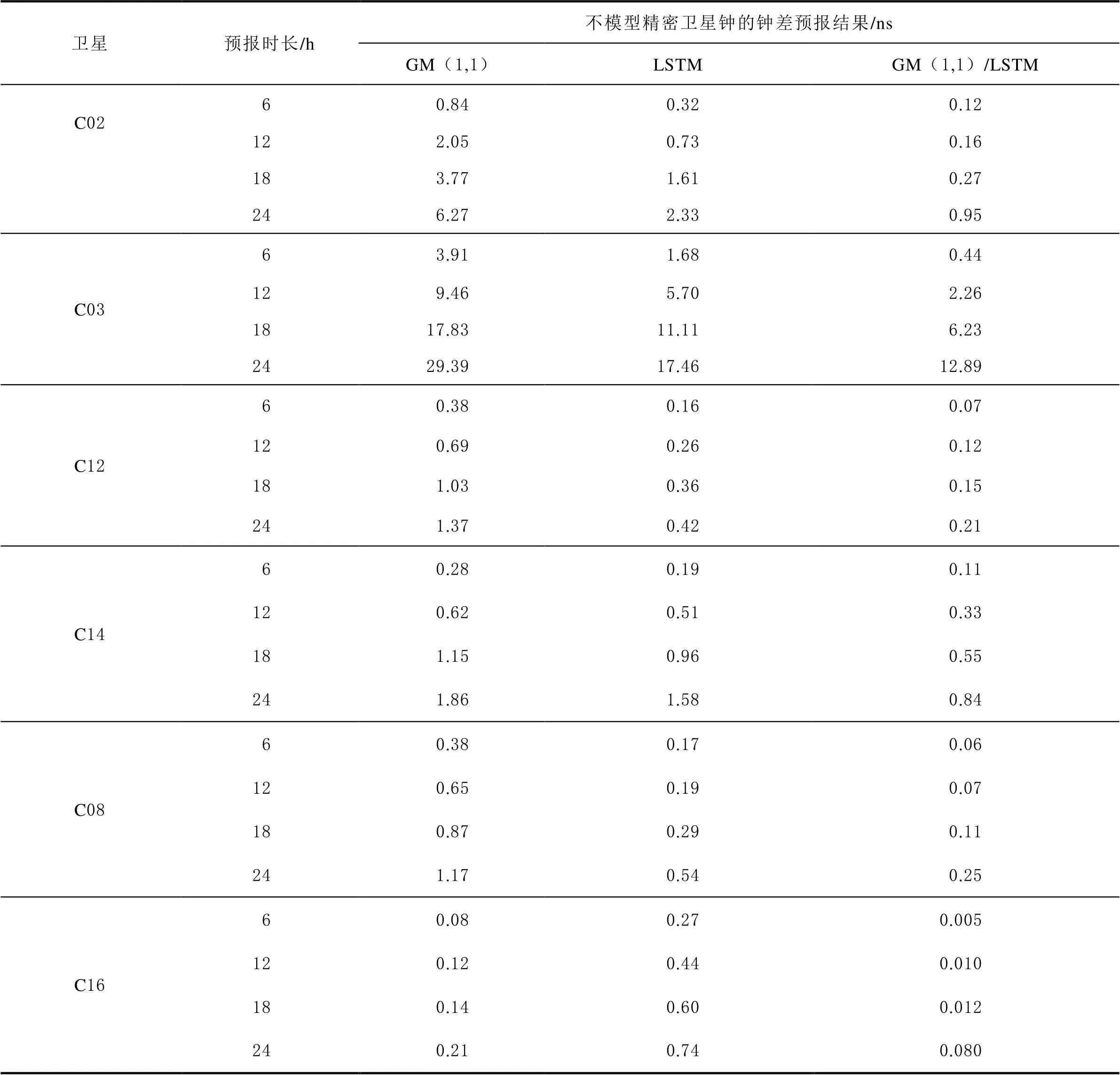
表1 精密衛星鐘差預報結果

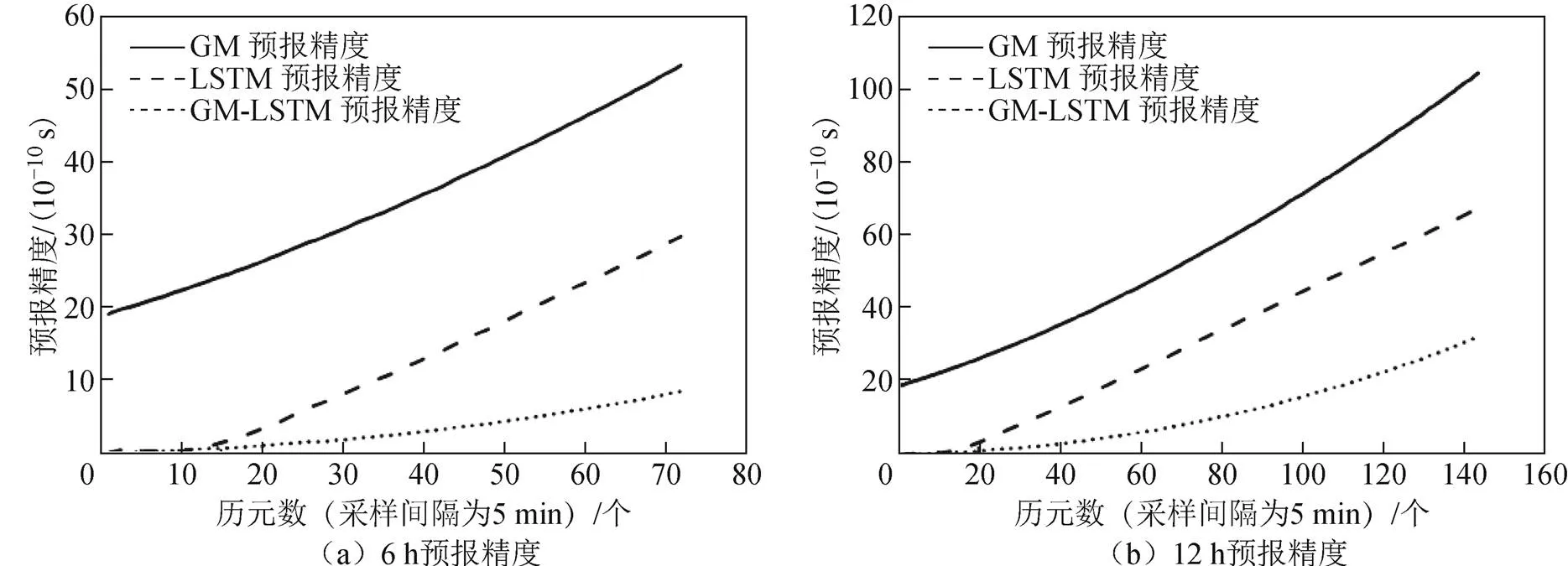
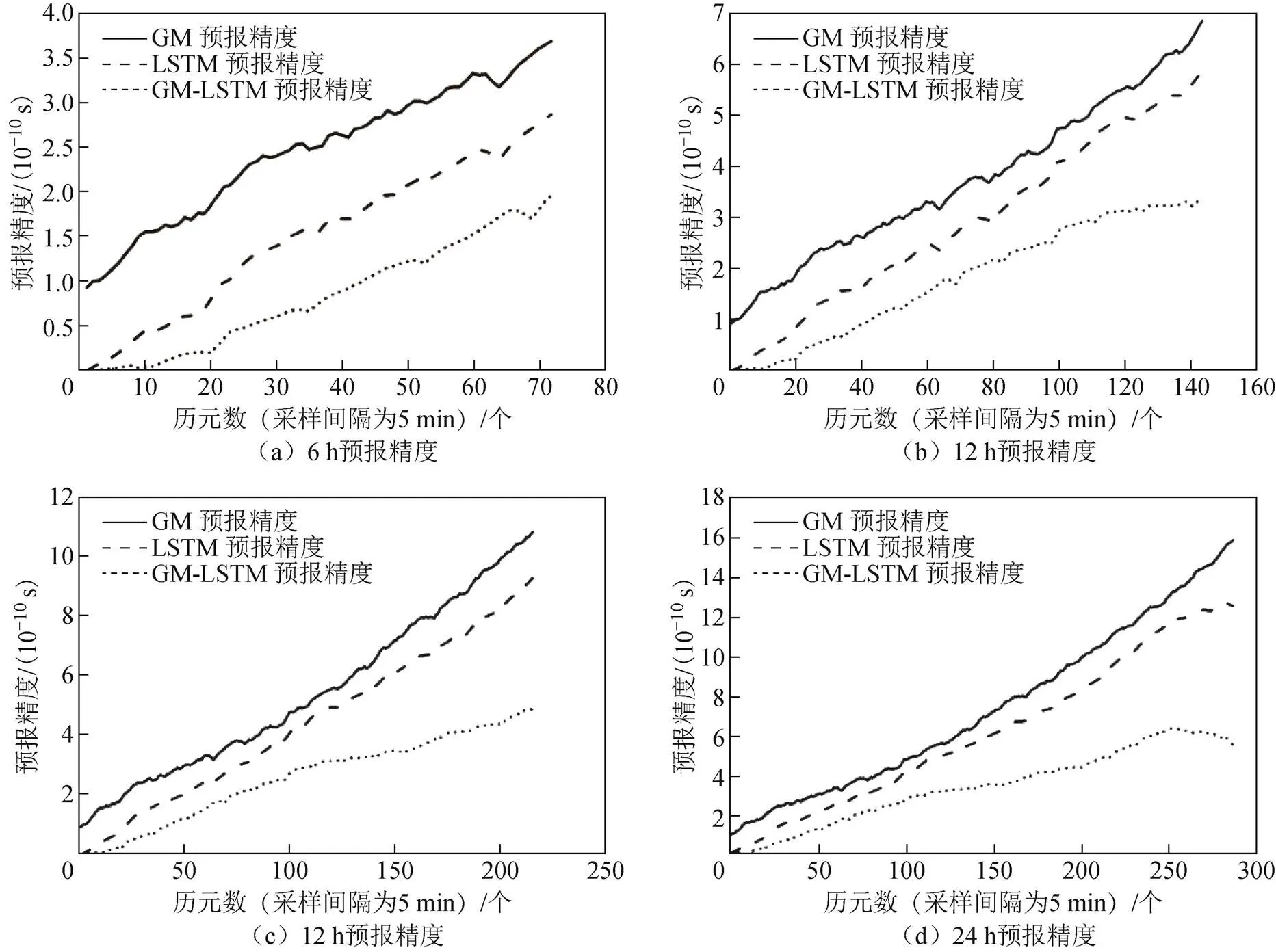
圖11 C14衛星預報6、12、18、24 h的預報誤差

結合圖10～圖12和表1可知：

1）以11月11日24 h的數據作為建模數據，分別對11月12日6、12、18和24 h的鐘差數據進行預報：GM（1，1）模型的預報平均誤差分別為0.98、2.26、4.13、6.71 ns；LSTM神經網絡模型的平均預報誤差分別是0.47、1.30、2.49、3.84 ns；GM（1,1）/LSTM組合模型的預報平均誤差分別為0.13、0.49、1.15、3.00 ns。無論是單一預報模型還是組合預報模型，其預報精度都會隨著數據的歷元增加而增大。GM（1,1）/LSTM模型預報結果除了在C03衛星的預報誤差超過1 ns，其余預報誤差均在1 ns以內，最小的為0.005 ns，平均精度達到亞納秒級。

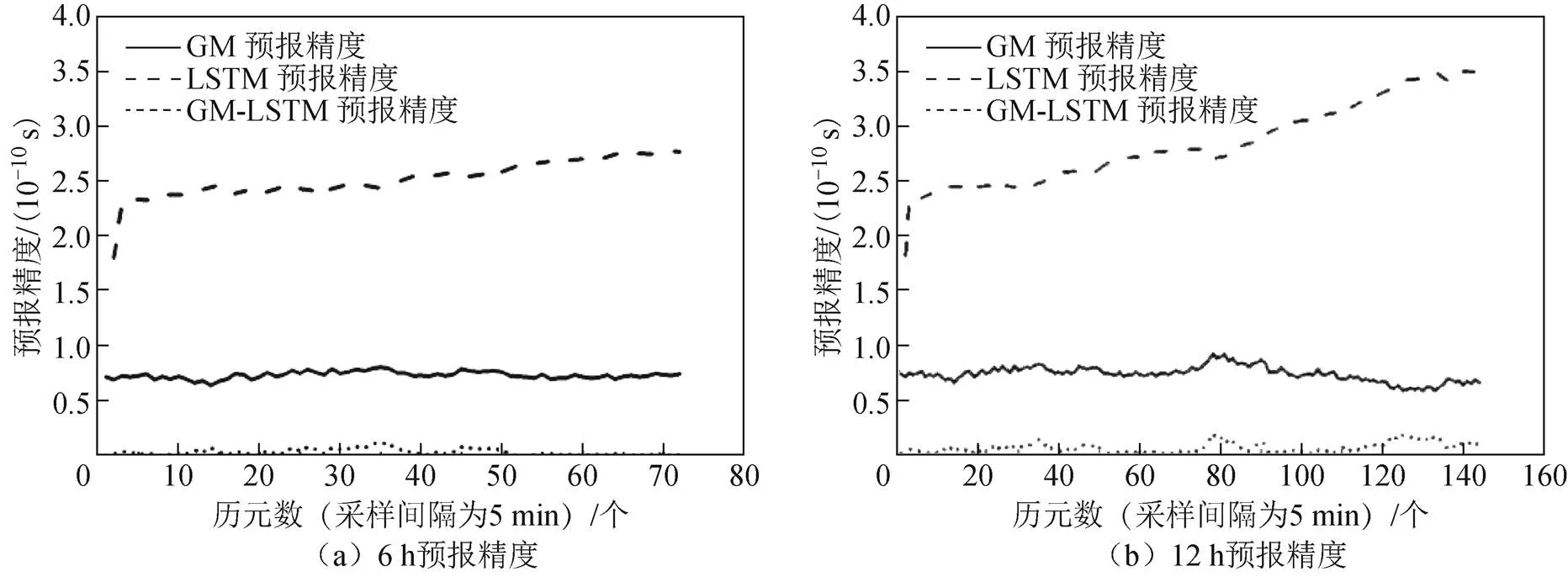
2）通過對比3個模型發現，不同模型對BDS精密鐘差的預報效果是不同的，而同種模型在不同的軌道、不同的衛星也有差異。具體而言，C03衛星是3種模型預報效果都不理想的衛星；C16衛星的LSTM神經網絡模型預測效果不如GM（1,1）模型；C16衛星是GM（1,1）模型和GM（1,1）/ LSTM模型預測效果最好的衛星；C12衛星是LSTM 神經網絡預報效果最好的衛星。故可以推測，同種預報模型的預報精度會因不同軌道衛星中可能存在影響模型的因素而受到影響。

3）通過對比3種衛星軌道發現，對于不同的軌道衛星，鐘差模型的預報效果存在差異。具體而言，以C08衛星和C16衛星為代表的IGSO軌道衛星是3種預報模型中效果最好的；以C12衛星和C14衛星為代表的MEO軌道衛星的鐘差預報模型預報效果次之；以C02衛星和C03衛星為代表的GEO軌道衛星的鐘差預報模型預報效果最不理想。故可以推測出同種軌道對不同的預報模型的影響是有差異的，可以根據軌道對衛星鐘差預報模型的影響來選取更為適合的精密鐘差預報模型。

4 結束語

針對單一預報模型在BDS精密衛星預報中存在著誤差累積的問題，提出了一種基于擬合殘差法的GM（1,1）/LSTM組合模型，可以降低預報模型的誤差累積。實驗結果顯示組合模型的精度高于單一模型，具體為：

1）以C02、C03衛星為代表的GEO衛星，GM（1,1）/LSTM組合模型的預報精度高于GM（1,1）模型和LSTM神經網絡模型。在不同時間段，與GM（1,1）模型精度相比分別提高了88.2%、79%、70%、61.2%；與LSTM神經網絡模型精度相比，分別提高了72.3%%、62.5%、48.9%、30.1%。

2）以C12、C14衛星為代表的MEO衛星，GM（1,1）/LSTM組合模型的預報精度高于GM（1,1）模型和LSTM神經網絡模型。在不同時間段，與GM（1,1）模型精度相比分別提高了72.7%、65.9%、83.3%、67.5%；與LSTM神經網絡模型精度相比，分別提高了48.6%、41.6%、47%、47.5%。

3）以C08、C16衛星為代表的IGSO衛星，GM（1,1）/LSTM組合模型的預報精度高于GM（1,1）模型和LSTM神經網絡模型。在不同時間段，與GM（1,1）模型精度相比分別提高了85.9%、89.6%、87.9%、76.1%；與LSTM神經網絡模型精度相比，分別提高了85.2%、87.3%、86.3%、74.2%。

[1] 符宏偉.GNSS靜態相對定位精度分析與比較[J]. 導航定位學報, 2021, 9(5): 114-120.

[2] 楊子輝, 薛彬. 北斗衛星導航系統的發展歷程及其發展趨勢[J]. 導航定位學報, 2021, 9(1): 1-4,

[3] 王建敏, 馬天明, 祝會忠. BDS/GPS整周模糊度實時快速解算[J]. 中國礦業大學學報, 2017, 46(3): 672-678.

[4] 廖汐琳, 李浩軍, 趙潤根. GPS衛星鐘差高精度模型化及在精密單點定位中的應用[J]. 大地測量與地球動力學, 2018, 38(8): 836-839.

[5] 王潤, 王井利, 呂棟. 導航衛星鐘差預報的Elman神經網絡算法研究[J]. 大地測量與地球動力學, 2021, 41(3): 285-289, 295.

[6] 劉永輝, 任彪, 徐景田. 基于遺傳神經網絡模型的超快速衛星鐘差預報[J]. 測繪地理信息, 2020, 45(6): 35-39.

[7] 于燁, 張慧君, 李孝輝, 等. 基于GM(1,1)和MECM組合模型的GPS衛星鐘差中短期預報[J]. 天文學報, 2018, 59(3): 19-30. DOI: 10. 15940/j. cnki. 0001-5245. 2018. 03. 002.

[8] 王建敏, 李特, 謝棟平, 等. 北斗精密衛星鐘差短期預報研究[J]. 測繪科學, 2020, 45(1): 33-41.

[9] 姜詩奇, 李博峰. ARIMA模型在衛星鐘差短期預報中的應用[J]. 導航定位學報, 2019, 7(4): 118-124.

[10] 趙增鵬, 楊帆, 張子文, 等. 粒子群算法優化的灰色神經網絡衛星鐘差預報[J]. 導航定位學報, 2018, 6(2): 53-56, 81.

[11] 雷雨, 趙丹寧, 蔡宏兵. 利用結構自適應極端學習機預報導航衛星鐘差[J]. 武漢大學學報(信息科學版), 2018, 43(5): 664-668, 718.

[12] 于燁, 黃默, 段濤, 等. 粒子群優化加權灰色回歸組合的衛星鐘差預報[J]. 哈爾濱工業大學學報, 2020, 52(10): 144-151, 182.

[13] 蔣玉祥. 冪函數變換的GM(1,1)模型在BDS衛星鐘差預報中的應用研究[J]. 全球定位系統, 2020, 45(2): 49-54.

[14] 牛樹華, 于燁, 黃默, 等. 基于誤差修正的GM(1, 1)導航衛星鐘差預報算法[J]. 艦船電子對抗, 2019, 42(4): 81-86.

[15] 祝會忠, 雷嘯挺, 李軍, 等. BDS參考站三頻整周模糊度單歷元確定方法[J]. 測繪學報, 2020, 49(11): 1388-1398.

[16] 宮曉春, 王宇譜, 王寧, 等. GPS衛星鐘差改正數實時預報算法[J]. 武漢大學學報(信息科學版), 2018, 43(6): 867-873.

[17] 王建敏, 李亞博, 祝會忠, 等. BDS衛星位置插值方法研究及精度分析[J]. 測繪科學, 2017, 42(12): 25-31.

[18] 潘澔, 高尚. GM(1, 1)模型的性質及改進[J]. 山東大學學報(理學版), 2021, 56(11): 38-43.

[19] 祝會忠, 雷嘯挺, 徐愛功, 等. 顧及GEO衛星約束的長距離BDS三頻整周模糊度解算[J]. 測繪學報, 2020, 49(9): 1222-1234.

[20] 龔蘭蘭, 凌興宏. 長短時記憶網絡公交短時客流預測實驗設計[J]. 現代電子技術, 2021, 44(22): 97-100.

Short-term forecast of precision clock difference for BDS

WANG Jianmin, BI Xiangxin, HUANG Jiapeng

（School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China）

Aiming at the problem that the accumulation of errors increases with the increase of time for the traditional single forecast model during the clock error prediction, the paper proposed a combination model of gray model GM(1,1) and long-short term mermory network (LSTM): the precision clock difference data of two consecutive days from three different satellite orbits of BeiDou navigation satellite system (BDS) downloaded by IGS (International Global Navigation Satellite Systems Service) Data Center at Wuhan University were modelled, GM(1,1) model was used to forecast firstly, and then the residual of GM(1,1) model was forecast again by LSTM neural network model; the forecast results by two models were reconstructed to obtain the final forecast results. Experimental result showed that the accuracy of GM(1,1)/LSTM combined model would be 60%～89% higher than that of single GM(1,1) model, and be 30%～88% higher than that of single LSTM neural network model.

clock error prediction; gray model (GM(1,1)); long-short term memory network (LSTM); combined model

P228

A

2095-4999(2023)01-0030-09

王建敏，畢祥鑫，黃佳鵬. BDS精密鐘差短期預報[J]. 導航定位學報, 2023, 11(1): 30-38.（WANG Jianmin, BI Xiangxin, HUANG Jiapeng. Short-term forecast of precision clock difference for BDS[J]. Journal of Navigation and Positioning, 2023, 11(1): 30-38.）DOI:10.16547/j.cnki.10-1096.20230105.

2022-05-09

國家自然科學基金項目（41474020）。

王建敏（1973—），男，甘肅酒泉人，碩士，副教授，研究方向為空間大地測量數據處理和變形監測。

畢祥鑫（1997—），男，內蒙古赤峰人，碩士研究生，研究方向為GNSS數據處理。