基于高斯核密度估計的典型負荷曲線形態聚類算法

嚴明輝， 謝雄， 李維劼， 吳滇寧， 崔雪， 潘舒宸

(1.昆明電力交易中心有限責任公司，昆明 523000; 2.武漢大學 電氣與自動化學院， 武漢 430072)

0 引 言

2019年國家發改委、能源局發布《關于深化電力現貨市場建設試點工作的意見》以來，首批8個電力現貨試點紛紛啟動結算試運行，現貨市場建設推進速度明顯加快[1]。在現貨市場結算中，實時要實時反映電力供需關系變化，因而有時實時電價波動會很劇烈，同時由于現貨市場采用價-量結算，故實時電量的準確性決定了現貨市場結算的準確性。由于各種計量裝置或傳輸問題，很多用戶的電量并不能實時獲得，這種用戶稱為非分時計量用戶，此時需要通過電力曲線將該類用戶的日電量分解至每日以15 min為間隔的分時電量，該電力曲線可稱之為典型負荷曲線。目前廣東電力市場非分時計量用戶的日電量分解計劃是對所有的用戶通過每日的峰平谷三個時段進行電量的比例分配[2]。這樣對一個用電規律明顯的大用戶來說，一個時段內的曲線時段上微小的波動引起的電費差距可能很大。相對日電量按固定比例分配，建立一個動態的每日96個點的典型負荷曲線模型能有效提高日電量分解準確率。由于每個區域電力市場包含了海量用戶的負荷數據，不能給每個市場化用戶建立其典型負荷曲線模型，如何通過有效的負荷曲線形態分類方法來把握不同用戶的用電特性，具有相同用電曲線的用戶選用相同的典型負荷曲線進行現貨市場日電量的分解；同時如何提高典型負荷曲線的日分時電量曲線的準確性成為了關乎現貨市場進一步深入推進的關鍵。

為了解決上述問題，本文選用負荷曲線形態聚類后的聚類中心作為簇內的典型負荷曲線用于簇內所有用戶的日分時電量分解。從而可以通過提高聚類中心描述同類簇下所有曲線的能力來提高所有用戶日分時電量分解時的準確性。目前國內外關于負荷曲線形態分類問題的研究較為完備，主要通過無監督學習的聚類方法獲得。包括快速密度峰值算法[3]、基于斜率提取邊緣[4]、模糊c均值聚類和譜聚類[5-7]等聚類算法和利用降維方法來提高聚類效果如強化學習機[8]、自編碼器降維[9]、奇異值分解降維[10]、自組織映射降維[11]等。傳統聚類算法為了提升分類效率，一定程度上犧牲了聚類中心描述同類簇負荷曲線的能力和準確性。如Kmeans算法是一種基于距離的無監督學習分類方法，其聚類中心是通過同類簇的均值法獲得，通過不斷迭代計算同類簇下曲線與聚類中心的歐式距離，來獲得分類結果[12]。聚類中心只是為了獲取分類結果的一個過程比較參數，聚類中心的描述能力仍可進一步提高。同時在傳統聚類算法中，核密度估計(Kernel Density Estimation，KDE)只用于選取Kmeans聚類的初始聚類中心，從而來提升分類效果[13]。但是只能保證初始聚類中心在第一次迭代計算中，描述能力是最好的。而在后續的迭代計算中，不能保證典型負荷曲線的簇內描述能力。

基于此，為了提升聚類中心描述同類簇的能力，本文將核密度估計的思想引入Kmeans聚類算法中的聚類中心每一次形成過程，將原有的均值獲取聚類中心升級為高斯核密度估計獲取最大概率的聚類中心進行迭代計算。典型負荷曲線獲取流程如圖1所示，利用電力負荷數據進行數據準備和改進Kmeans算法聚類，最后以云南省電力計量數據為例，對提出的算法與傳統聚類算法、傳統日電量分解方法進行了比較。結果顯示基于核密度估計改進聚類中心的Kmeans-KDE算法獲得的典型負荷曲線在用于現貨市場日電量分解時準確性更高。

圖1 典型負荷曲線形成框架Fig.1 Typical load curves frame

1 負荷數據準備

為了解決非分時計量用戶的電量分解問題，選擇具有相似用電規律的分時計量用戶的典型負荷曲線提供其進行結算。如不具備分時計量的超市參與現貨市場時，需要根據具有分時計量超市的典型負荷曲線進行日電量的分解。故需要選擇具有分時計量能力的樣本用戶，為了樣本用戶能充分模擬真實的全省負荷，樣本用戶的選取涵蓋了各個行業，各個電量等級。由于電力計量狀況不一，存在漏數、串數等異常情況，需要對各樣本數據進行預處理。

1.1 數據預處理

1.1.1 異常數據處理

對于異常數據，根據計量值累加遞增原則即下一個時刻的計量值大于等于此刻的計量值小，記錄異常值位置，對該位置的數據做缺失值處理。

1.1.2 缺數處理

對于用戶負荷電量缺數較少的情況，采用三次樣條插值法[14]進行插補。對于缺值較多的用戶，采用垂直修復法進行修復。即選用前一周同一時刻對應的負荷值作為此刻的負荷值。對于缺值太多的用戶不宜選為樣本用戶。

1.2 典型負荷曲線提取

1.2.1 提取樣本日負荷曲線

經過數據預處理后，得到了樣本用戶全年一共35 040個時間序列點計量數據。為了得到特定場景下(特定月份)的樣本典型負荷曲線，需要進一步對該樣本用戶的不同場景(工作日、休息日、節假日)進行日負荷曲線提取。采用基于高斯核函數概率密度分布的方法進行負荷曲線提取。以6月份的工作日場景為例。該場景下任一個時序點的電量等于該月22個工作日的電量數據進行概率密度的疊加。

其中Gaussian核函數K，其計算公式為：

(1)

計算該用戶歷史負荷數據第k時刻負荷值xk_num對應的概率密度函數fk(xk_num)，其表達式為

(2)

式中K為高斯核函數；T為時序k下的樣本點數目；h為帶寬；xk_num∈[xk_min,xk_max]；xik為第i日k時刻的負荷值；xk_min為該用戶歷史負荷數據第k時刻的負荷最小值；xk_max為該用戶歷史負荷數據第k時刻的負荷最大值。

根據式(2)，形成最大概率密度曲線向量，Xi_mp=[xi_mp_1,xi_mp_2,…xi_mp_k,…,xi_mp_96]T，這條最大概率密度曲線作為該樣本用戶的典型負荷曲線，其中xi_mp_k為fk(xk_num)取最大值時xk_num對應的數值。

1.2.2 數據標準化

樣本用戶使用電量的數量級具有較大差異，而典型日負荷曲線提取是為了把握該樣本用戶的負荷規律，即目的在于曲線的形狀而非曲線的電量值。故可以通過數據標準化，對數據按比例縮放，使之落入一個特定區間進行曲線形狀的描述。文中設置所有樣本用戶一天內的96個時序用電量之和為1 000 kWh，便于不同量級的用戶能夠進行比較和加權，如式所示。

(3)

1.2.3 負荷曲線平滑

用戶用電數據存在用戶數據由于其一定的用電隨機性，負荷曲線容易出現一定的上下波動的情況，而進行負荷曲線預測時，希望把握負荷的曲線變化規律，因此部分曲線出現的噪音點將會干擾負荷波動形態的判斷。鑒于上述問題，最后使用高斯濾波(Gauss Filter, GS)進行用戶典型曲線的平滑[15]。

原有的用戶計量數據為不完整的電量數據，經過前文所述的數據預處理后，可得到任意月份的典型日負荷曲線。經過平滑后的某超市2018年6月的工作日典型負荷曲線如圖2所示。

圖2 某超市2018年6月工作日典型負荷曲線Fig.2 Typical load curve of working days in June 2018 of supermarktet

2 基于核函數估計的Kmeans聚類

2.1 主成分分析法降維

數據降維可提升后續聚類算法的效率，同時能夠舍棄掉噪聲影響的數據。文獻[16]中指出對于負荷曲線降維，主成分分析降維可取得最佳效果；因而選用主成分分析法進行用戶數據降維。

主成分分析基于最大可分性，將樣本用戶在超平面上實現可分。PCA算法流程如表1所述。其中，降維后維數d根據特征向量的描述能力決定。

表1 主成分分析算法流程Tab.1 Principal component analysis algorithm flow

2.2 改進kmeans聚類算法

2.2.1 聚類有效性評價

數據集中含有N條樣本負荷曲線，每條負荷曲線可以表示為96維的向量。由于聚類的樣本負荷曲線沒有標簽，為無監督學習。故為了衡量聚類的效果，引入聚類有效性指標有誤差平方和(Sum of Squared Error，SSE)、Davies-Bouldi 指標(Davies-Bouldin Index，DBI)等[17]。根據聚類有效性指標確定最佳聚類數目，實現kmeans聚類數目的準確輸入。

(1)SSE指標

誤差平方和SSE用于衡量簇內各子類至聚類中心的歐氏距離，即：

(4)

(2)DBI指標

DBI指標能有效描述簇內的相似性和簇之間的相差性。

(5)

式中:

(6)

式中d(Xk)和d(Xj)為簇內樣本內部距離；d(ck,cj)為聚類中心的距離；IDBI越小表示聚類效果越好。

2.2.2 基于核密度估計的Kmeans聚類算法

傳統Kmeans聚類算法是根據歐式距離來對樣本的相似性進行的分類的方法。算法流程如表2所示。在傳統Kmeans算法中第10步計算新的均值向量時，采用等權重平均值疊加形成的新的聚類中心。然而在實際中，均值法聚類中心提高了算法效率，但是對聚類中心的聚類質量也有一定下降。為了提高對典型負荷曲線描述用戶用電特點的準確性。基于概率統計的思想，提出一種新的聚類中心形成方法，如圖3所示。采用高斯核函數概率密度分布函數擬合樣本最大概率分布函數，然后根據簇內的其他曲線與最大概率曲線的概率分布進行加權疊加，獲得新的聚類中心形成數據的劃分。結果顯示新聚類中心能更精準描述簇內用戶的負荷曲線。

圖3 改進Kmeans聚類算法流程Fig.3 Process of clustering center algorithm for kernel density estimation

表2 Kmeans算法流程Tab.2 Kmeans algorithm flow

新的聚類中心形成過程包括

(1)根據式(2)計算時序k的負荷值xk_num對應的概率密度函數fk(xk_num)，其中K為高斯核函數，T為時序k下的樣本點數目，h為帶寬；xik為簇內的第i條曲線時序k的負荷值；xk_min為簇內歷史負荷數據第k時刻的負荷最小值；xk_max為簇內歷史負荷數據第k時刻的負荷最大值。

(2)迭代計算各個時刻(1～96)的概率密度函數，形成最大概率負荷曲線Xi_mp=[xi_mp_1,xi_mp_2,…,xi_mp_96]T，其中xmp_k為fk(xk_num)取最大值時xk_num對應的數值。

(3)計算簇Cλj內第i條負荷曲線Xi=[xi1,xi2,…,x96]T相較于最大概率負荷曲線Xi_mp=[xi_mp_1,xi_mp_2,…,xi_mp_96]T的權重wi。

(7)

(4)對簇內所有的負荷曲線進行加權疊加，以獲得新的聚類中心。

(8)

3 算例分析

文中選用從2018年7月1日至2019年7月1日的云南全省16市1 250,家用戶涵蓋鋼鐵、冶煉、金屬等大工業用戶以及超市、酒店等一般工商業用戶以15 min為粒度的負荷計量數據。經過前述提及的數據預處理、提取的典型負荷曲線、數據標準化、曲線平滑后得到的負荷曲線數據進行基于核函數估計的Kmeans聚類分析。

3.1 聚類質量評價

首先，對負荷曲線經進行聚類有效性檢測，結果如圖4所示，在不同聚類數目時，DBI指標呈現出波動性，當聚類數為8時，DBI指標取至極小值。此時意味著聚類效果最好。因而選擇聚類數8進行下一步的聚類。

圖4 DBI指標確定最佳聚類數目Fig.4 Davies-Bouldi Indexes determine the optimal number of clusters

3.2 負荷數據集聚類結果分析

對樣本庫典型負荷曲線進行主成分分析后，原有的數據進行了降維。如圖5所示，原有的一天96維度的負荷數據經主成分分析后，在保持95%的貢獻率下，降維成了13維。此時描述負荷曲線能力沒有下降，低維的數據描述了原有的高維曲線特性。

圖5 主成分分析結果Fig.5 Principal component analysis results

由于負荷曲線以15 min為分解粒度，故每日共計有96個時序點。每個點對應的值為該15 min內的用電量。利用降維后的負荷數據作為聚類算法的數據矩陣，運用基于核密度估計的Kmeans算法進行聚類。結果如圖6所示。

圖6 聚類結果示意圖Fig.6 Schematic diagram of clustering results

結果顯示負荷曲線形態分類效果較好。用電曲線大致分為單峰(第三類)、雙峰(第一類、第六類)、三峰(第八類)、避峰(第七類、第五類、第四類)、平峰(第二類)等。大多數大工業用戶為追求效率最大化選用全天24小時連續運行，因而呈現出單峰。部分工業用戶對電價敏感采用峰谷運行方式，白天少用電，晚上多用電，呈現出避峰的典型負荷曲線形態。對于超市、商業綜合體等營業時間考慮人流量和白天的活動時間，從早上至晚上營業。因而呈現出單峰或者雙峰的形態。云南采礦業發達，對于小型的頁巖磚廠以及小工業用電，其用電特性與工作人員的休息時間息息相關，呈現出三峰的用電曲線形態。聚類結果與實際全省不同用戶的不同用電規律相契合。

3.3 曲線描述能力比較

改進kmeans-KDE算法曲線描述能力有了進一步提高，典型負荷曲線能更好的用于日電量的分解。為進一步對新算法下的典型負荷曲線的描述能力有一個更直觀的比較，通過不同聚類中心形成方法、不同算法、不同典型負荷曲線分解實例來對改進kmeans-KDE算法的典型負荷曲線描述能力做定量的比較。

選用均值法、正態核(正態分布)[12]、高斯核下產生聚類中心迭代對最終聚類結果的影響進行比較。結果如圖7所示，對比可知三種方法產生的聚類中心的形狀曲線大致走勢相同，但是正態核描摹的聚類中心出現了多處局部突變為零。引入SSE指標量化對比三類方法的誤差平方和，結果如表3所示，高斯核密度估計的聚類中心相較傳統的均值法聚類中心，誤差平方和SSE更小，相較能更好的描述簇內各曲線的相似性。聚類中心作為典型負荷曲線描述能力更強，典型負荷曲線用于現貨市場電量分解時，準確性更高。

圖7 高斯核估計與其他方法聚類中心比較Fig.7 Comparison of Gaussian kernel estimation and other method cluster center

表3 三類方法SSE指標比較Tab.3 SSE index comparison of three methods

選取傳統算法聚類和新算法在同一個數據集進行聚類，結果比較如表4所示。經過降維后的基于核密度估計的Kmeans算法相較其他聚類算法雖然在耗時上有所增加，但是在SSE指標聚類中心的誤差平方和最小，意味著在同一個簇的各曲線的相似度更高。DBI指標較小，在簇內相似性和簇間相異性均能有較為優異的效果。意味著核密度估計改進聚類中心的新算法相較傳統聚類算法不僅提高了典型負荷曲線的描述能力，同時提高了負荷曲線形態分類的效果。

表4 算法結果比較Fig.4 Comparison of algorithm results

算法結果中的各項指標印證了典型負荷曲線相較傳統算法描述能力有了提高。為了比較在具體實例中傳統算法曲線分解、峰谷平分解、改進Kmeans-KDE算法曲線分解日電量的準確性，以云南省某鋁冶煉廠某一日真實計量值為例，負荷采集間隔為15 min。如圖8所示。

圖8 某用戶某日真實負荷曲線Fig.8 The real load curve of a user on one day

該用戶日電量總計為223 732.5 kW·h。當用戶該日所有電量缺失時，需要恢復該日96點真實電量用戶現貨結算，由于前文采用了數據標準化，故電量恢復公式如下所示:

用戶該日真實負荷曲線=該日電量/1 000×96點典型負荷曲線值

當該日分時計量值缺失時(模擬非分時計量用戶)，選用三種不同方法進行真實負荷描述能力的比較。

(1)峰谷平曲線D1分解

根據廣東電力市場峰谷平曲線D1[2]進行日電量均分分解，即將日電量平均分解至每日峰段、平段和谷段。分解結果如圖9所示。

圖9 峰谷平D1曲線-電量分解結果Fig.9 Peak valley level D1 curve-result of electric quantity decomposition

(2)傳統算法負荷曲線分解

以傳統算法中Kmeans算法為例[12]，獲得該樣本用戶的分類結果，利用其典型負荷曲線對日累計電量進行分解，日電量分解結果如圖10所示。

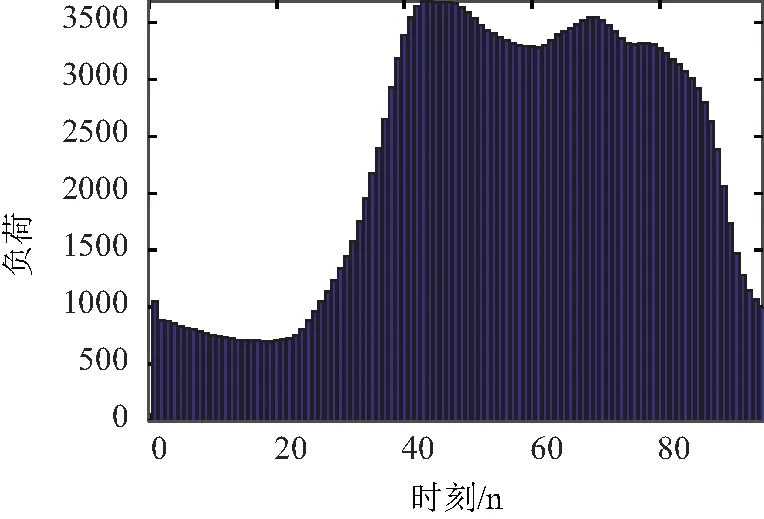
圖10 傳統聚類算法-電量分解結果Fig.10 Traditional clustering algorithm-power decomposition results

3)改進Kmeans-KDE算法典型負荷曲線分解

利用改進Kmeans-KDE算法提取的典型負荷曲線對日累計電量進行分解，日電量分解結果如圖11所示。

圖11 改進Kmeans-KDE算法-電量分解結果Fig.11 Improved Kmeans-KDE algorithm-power decomposition results

以分解后的電量曲線與真實負荷曲線的96個點誤差率平均值作比較，其中誤差率計算方法如式(9)所示，計算結果如表5所示。

表5 不同曲線分解方法誤差率Tab.5 Error rate of different curve decomposition methods

誤差率=|真實值-分解值|/真實值

(9)

改進Kmeans-KDE算法獲得的典型負荷曲線用于用戶日電量分解時，相較其他方法得到的日分時分解曲線，誤差率更低，典型負荷曲線描述真實負荷波動時，描述能力更強。

4 結束語

為了解決現貨市場背景下，市場化用戶日電量分解的準確性問題,文中提出了基于核密度估計改進Kmeans算法的典型負荷曲線形態聚類方法，利用高斯核密度估計獲得聚類中心代替原有的均值法獲得聚類中心，并將其作為典型負荷曲線參與現貨市場日分時電量分解。最后，運用云南省樣本用戶計量數據進行算例分析，結果顯示，文中所提算法不僅負荷曲線形態分類效果較好，同時獲取的典型負荷曲線參與現貨市場的日電量分解時準確性更高，可為現貨市場結算試運行提供了相應的技術撐。