COVID-19分數階群體時滯模型的穩定性分析

魏慶棟，王 忠，湯家軍，陳海燕

（1.火箭軍工程大學，西安 710038；2.中國礦業大學（北京），北京 100083）

自新冠疫情防控進入常態化以來，使用合適的數學模型來描述和預測病毒傳播情況，評估疫情防控措施效果已經成為學界共識。本文通過研究新冠肺炎傳播的動力學特性，引入時滯參數，結合分數階模型，構建了一種描述新冠肺炎傳播狀況的分數階群體時滯模型。

1 模型的建立與分析

1.1 分數階模型的建立

根據COVID-19的傳播特性，在傳染病動力學SIR模型中引入潛伏期患者，即已經感染病毒但是尚未表現出癥狀的患者，也可以稱為無癥狀患者，因此在模型中增加時滯參數，根據現有經驗，在經過一段時間的潛伏后，會有一定比例的潛伏患者最終發展成為確診病例[1]，這部分人群對最終結果的影響離不開潛伏周期這一因素，用參數τ來表示，在完成整數階模型后，修改得到下列分數階模型

上述系統當t=0時，會滿足下述的初值條件

其中，S（t）為易感人群t時刻的人數，A（t）表示在t時刻無癥狀感染者的人數，I（t）為在t時刻有癥狀的感染者的人數，R（t）為恢復健康的人數，λ為正常人群中的自然增長速率下的增長人數，θ為無癥狀感染者轉換為有癥狀感染者的概率，β1、β2分別為正常人群和無癥狀感染者與有癥狀感染者接觸后被感染的概率，δA、δI分別為無癥狀被感染人群和有癥狀被感染人群的恢復率，d、dA、dI分別為正常人群、無癥狀感染者和有癥狀感染者的死亡率。在本系統中引入時滯參數τ來模擬模型的潛伏期參數。

1.2 模型的分析

根據系統1（公式（1）所示，下同），可以得出2個平衡點，一個無病平衡點E0=（x0，0，0，0），其中，一個地方病平衡點E*=（S*，A*，I*，R*），該平衡點滿足

在對上述2個平衡點進行分析前，利用下一代生成矩陣法求出該模型的基本再生數為

1.2.1 平衡點的非負性分析

定理1.2.2對于系統1來說，地方病平衡點E*有以下結論，當R0＞1時，地方病平衡點E*=（S*，A*，I*，R*）是非負的。

證明：對地方病平衡點E*=（S*，A*，I*，R*）進行求解，得到

由于參數非負，因此S*≥0。對于A*，I*，R*，根據等式，可以得知主要取決于λ－dS*。當R0≥1時，同時因為

為證明分數階模型平衡點的穩定性可使用如下引理：

引理1[2]分數階系統的平衡點滿足局部漸進穩定的性質，當且僅當在相應平衡點處的Jacobi矩陣J=的所有特征值λi滿足條件。

1.2.2 無病平衡點的局部漸進穩定性

設特征值為sα，則模型1（公式（1）所示，下同）在無病平衡點E0處的特征行列式為

定理1.2.3模型1滿足下列結論，當τ≥0時，該模型的無病平衡點E0有如下結論：

如果R0＜1，則E0是局部漸進穩定的。如果R0≥1，則E0是不穩定的。

證明：根據特征矩陣（3），進行推導化簡可以得到

根據（sα+d）2，得到特征值因此。

將行列式部分用下列形式進行表示

P1（s）=0存在2個根，一個根為一定有負實部；另一個根，當R0＜1時因此此時它也一定有負實部。

1.2.3 地方病平衡點的局部漸進穩定性

當R0＞1時，模型1存在一個非負的地方病平衡點E*=（S*，A*，I*，R*），設特征值為sα，則地方病平衡點E*處的特征行列式為

先討論τ=0時，令γ=sα，得到

其中參數d1，d2，d3可以表示為

而m11，m12，m13，m21，m22，m32，m33可以表示為

因此當τ=0時，E*有如下性質：當R0＞1時，如果式（8）滿足n=3時的霍爾維茨準則，即式（8）的所有根都具有負實部，則E*是局部漸進穩定的。

當τ≠0時，根據特征行列式（6），可以化解得到如下的等式

將虛部和實部分開得到

其中參數為

對式（10）經過推導化簡，令w2α=y，得到了如下的結果

進一步簡化為

其中各參數表示意義如下

因此當式（13）滿足霍爾維茨準則時，式（13）的根均為負值，則式（10）的解中存在負實部，此時地方病平衡點是局部漸進穩定的，綜上給出如下定理。

定理1.2.4對于模型1的地方病平衡點E*，在R0＞1的情況下，若式（8）與式（13）均滿足引理1，則可以得出結論，當τ≥0時，E*是局部漸進穩定的。

2 數值模擬與結果

為便于后續計算，首先通過NSFD算法對分數階模型進行離散化處理[3]，然后進行數據模擬，主要模擬各類人群隨時間變化的發展趨勢。以此來研究帶有時滯的分數階模型的平衡點的穩定性。分2種情況對模型進行數值模擬，一是對模型（1）在不同的階數下隨時間變化的情況進行模擬，二是對模型在同一分數階下，取不同時滯時，隨時間變化的情況進行模擬。

2.1 對無病平衡點的數值模擬

由于對無病平衡點進行分析時要使得不存在非負的地方病平衡點，因此參數設置為λ=5，d=0.04，為增加結果的可靠性，同時設置了幾組不同的階數進行對比試驗，將分數階階數分別設置為α=0.7，0.8，0.9，其余參數分別為β1=β2=0.001，d1=0.03，d2=0.1，δA=0.4，δI=0.3，θ=0.6，τ＝10。根據參數設置，此時基本再生數R0≈0.3＜1，且λ-dS*＜0，因此顯然不存在非負的地方病平衡點，且E0=（125，0，0，0），根據定理1.2.3，在滿足τ≥10的情況下，當R0＜1時，無病平衡點是局部漸進穩定的。利用MATLAB進行數值模擬，結果顯示與理論相符合。因此按照這個趨勢發展，各部分人群都將趨于穩定，其中只有易感人群還是非零的，其余的都將趨于零。

其余參數不變，將階數設置為0.9，將時滯分別設定為τ=5，10，30，此時模擬結果各數值都趨于穩定，與定理1.2.3相符合。

2.2 對地方病平衡點的數值模擬

在對地方病平衡點進行模擬時，需要對參數重新進行修正，選擇參數λ=10，d=0.02，分數階階數分別為α=0.7，0.8，0.9，其余參數保持不變，最終數值模擬的結果如圖1所示。

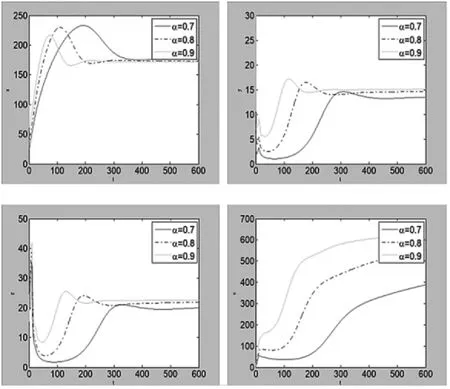
圖1 地方病平衡點下模型各變量在取不同階數時隨時間變化的圖

此時基本再生數R0=1.16＞1，顯然存在非負的地方病平衡點E*=（172，15，23，651）。將假設參數帶入式（13）后，根據定理1.2.4，此時地方病平衡點是局部漸進穩定的。顯然數值模擬的結果與理論相符合，在該情況下，隨著時間的發展，各部分人群都將趨于穩定，但是依然存在患者和無癥狀的潛伏者，此時疫情防控依然不能松懈。

其余參數不變，將階數設置為0.9，將時滯分別設定為τ=5，10，30，數值模擬結果如圖2所示，此時，τ≥0，地方病平衡點都是局部漸進穩定的。模擬的結果與理論相符合。

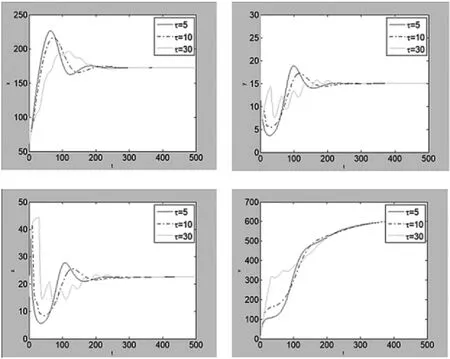
圖2 地方病平衡點下模型各變量在取不同時滯時隨時間變化的圖

3 結論

根據構建的分數階模型，得出了其有2個平衡點，對2個平衡點的局部漸進穩定性分別進行了討論。通過計算求出了基本再生數R0，證明了在τ≥0的情況下，無病平衡點E0在R0＜1時，是局部漸進穩定的，而當R0≥1時，無病平衡點E0不是局部漸進穩定的；對于地方病平衡點E*來說，當R0＞1時，若式（8）與式（13）中參數均滿足引理1，可以得出結論，當τ≥0時，E*是局部漸進穩定的。同時根據2種情況對模型進行了模擬，一種是分數階階數不同，另一種是保持分數階階數相同但取不同的時滯，通過模擬驗證了之前推導的平衡點穩定性的結論是正確的。此外，通過分析模擬，證明了基本再生數R0這一指標的重要性，為了更好地防控疫情，需要采取措施力求將R0保持在1以下。