基于北斗衛星外輻射源的目標直接定位算法

閆 攀，栗強強，閆會峰

(1. 重慶移通學院 大數據與計算機科學學院，重慶 401520；2. 重慶郵電大學 軟件工程學院，重慶 400065)

0 引言

基于外輻射源的無源雷達自身不輻射電磁波，是借助環境中已有的第三方輻射源照射到目標所形成的回波來探測和定位目標。目前，研究較多的外輻射源包括廣播電臺[1]、通信基站[2]、雷達[3]和衛星輻射源信號[4-5]等，其中，北斗衛星導航信號作為無源雷達外輻射源具有覆蓋范圍廣、全天時全天候、距離和速度分辨率高等優勢[6]。加之隨著北斗衛星導航系統的不斷完善以及戰時安全性的考慮，基于北斗衛星信號的無源雷達系統近年來備受關注。本文針對基于多顆北斗衛星外輻射源的無源雷達目標定位問題進行研究。

目前，針對基于北斗衛星外輻射源的無源雷達目標定位問題的研究主要可以分為2類：兩步定位[7-14]和直接定位[15-17]。兩步定位是一類傳統的定位方法，其基本框架是：第一步利用空時域處理[7]、互模糊函數[8]、動目標檢測[9]和拉頓-傅里葉變換[10]等參數估計方法從無源雷達接收到的北斗衛星直達波信號和相應的目標回波信號中提取出時延、多普勒等定位參數；第二步基于提取出的定位參數，然后通過無跡卡爾曼濾波[11]、總體最小二乘[12]、遞推總體最小二乘[13]和約束總體最小二乘[14]等估計算法，從中估計出目標的位置參數。在高信噪比條件下，兩步定位具有良好的定位性能；然而，兩步定位也存在著一些固有缺陷，即從信息論的角度來看，兩步處理體制會損失一部分信息，導致最終目標定位誤差增大，特別是在低信噪比條件下或信號采樣點數較低時。近年來，隨著通信傳輸帶寬和芯片計算能力的提升，以文獻[15-17]為代表的直接定位方法開始得到越來越多的關注，其基本思路是從無源雷達接收到的直達波和目標回波信號中直接估計出目標位置參數。由于無需估計中間定位參數，直接定位避免了額外的信息損失，因此相比于傳統兩步定位算法具有更高的定位精度和穩健性。然而，文獻[15-17]中的直接定位算法假設外輻射源信號為一般未知信號波形，并未利用北斗衛星信號結構的先驗信息[18]，這顯然限制了目標定位精度。因此，有必要針對基于北斗衛星外輻射源的無源雷達目標定位問題進行進一步研究。

本文針對基于北斗衛星外輻射源的無源雷達目標定位問題，提出一種聯合北斗衛星信號結構的直接定位算法。該算法將接收信號進行分時處理，利用北斗信號結構已知的特點，重構純凈直達波信號，繼而利用純凈直達波信號對目標回波信號進行脈沖壓縮。依據最大似然準則以及目標-接收機-外輻射源位置幾何關系，構建脈壓信號數據關于目標位置-速度估計的似然函數，通過尋找似然函數的全局極大值目標位置和速度估計。此外，本文還推導了目標位置-速度估計的克拉美羅界(Cramér-Rao Lower Bound，CRLB)。通過仿真實驗結果驗證本文算法的有效性和相比于現有算法的性能優勢。

1 信號模型

本文考慮的基于北斗衛星外輻射源的無源雷達系統由M顆北斗衛星外輻射源和1個地面靜止的接收機組成，其幾何結構如圖1所示。

圖1 基于北斗衛星的無源雷達目標定位場景Fig.1 Target localization scenario of passive radar based on BeiDou satellites

北斗系統的導航電文經過偽隨機序列(Pseudo Random Noise, PRN)碼擴頻后，采用正交相移鍵控(Quadrature Phase Shift Keying, QPSK)的方式調制到載波上。因此，第m顆衛星發射的導航信號可以表示為[17]：

sm(t)=gm(t)dm(t)ej(2πfct+ψm)，

(1)

式中，gm(t)表示測距碼(擴頻碼)；dm(t)表示數據碼(導航電文)；fc表示信號載頻，ψm表示初始相位。

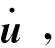
R0,m(t)=‖tm(t)-r‖ ，

(2)

第m顆北斗衛星到目標的距離為：

R1,m(t)=‖tm(t)-u(t)‖ ，

(3)

目標到接收機的距離及其變化率分別為：

R2,m(t)=‖r-u(t)‖ ，

(4)

那么，來自第m顆北斗衛星的信號到達接收機的直達波路徑和目標反射路徑的時延分別為：

(5)

(6)

s0,m(n,i)=gm[tf-τ0,m(ts)]dm[ts-

τ0,m(ts)]ej[2πfc,mτ0,m(ts)+ψm]，

(7)

s1,m(n,i)=gm[tf-τ1,m(ts)]dm[ts-

τ1,m(ts)]ej[2πfc,mτ1,m(ts)+ψm]。

(8)

對于本文基于M顆北斗衛星輻射源的無源雷達系統，接收機的直達波信道和目標信道中會同時接收到來自M顆北斗衛星輻射源的信號。因此，直達波信道和目標回波信道接收信號分別表示為：

(9)

(10)

式中，a0,m(n)和a1,m(n)分別為直達波信道和目標回波信道對應的幅度衰減系數；w0(n,i)和w1(n,i)分別表示直達波信道和目標回波信道中的噪聲。

2 直接定位算法

在一般無源雷達中，純凈的直達波信號通常是未知的。然而，北斗衛星信號作為一種數字調制信號，其信號結構是已知的，這使得在接收端可以實現直達波信號的重構，利用重構的純凈直達波信號對目標回波信號做相關，實現目標通道中不同外輻射源信號的分離，最后利用純凈直達波信號和分離后的目標回波信號實現目標的高精度直接定位。因此，本文提出一種聯合北斗衛星信號結構的直接定位算法。

2.1 信號重構

如式(10)所示，來自不同衛星的信號在時域上是混疊的。為了分離混疊的信號，需要利用北斗導航系統碼分多址的信號特點。不同的衛星對應的輸出序列，在接口文件中已詳細規定[18]。

由于直達波信號的信噪比較高，因此可以按照北斗信號處理的標準流程得到來自第m顆衛星發射的導航電文dm(ts)。另一方面，由于衛星-接收機的位置參數已知，因此按照式(5)可以得到直達波信號的時延τ0,m(ts)，繼而可以重構出純凈的直達波信號：

τ0,m(ts)]ej[2πfc,mτ0,m(ts)+ψm]。

(11)

在重構出來自第m顆衛星直達波信號后，將式(11)與式(10)中的回波信號做相關。由于來自不同北斗衛星的信號是正交的，因此不同衛星的信號相關之后結果為零。從而得到式(10)與式(11)做相關后的等效脈沖壓縮信號，表示為：

a1,m(n)pm(n,k)+wm(n,k)，

(12)

式中，符號*表示復共軛；pm(n,k)和wm(n,k)分別表示第m顆衛星直達波信號與目標回波信號、噪聲相關輸出結果，其具體表達式為：

χm[τm(ts)]ej[2πfc,mτm(ts)]，

(13)

dm[ts-τm(ts)]dtf，

(14)

τm(ts)=τ1,m(ts)-τ0,m(ts)，

(15)

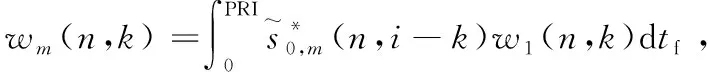
(16)

式中，χm[τm(ts)]表示慢時間nPRI對應的等效脈沖信號偽隨機碼自相關；τm(ts)表示雙基地時延，可以看出，由于目標和衛星的運動，雙基地時延τm(ts)是隨慢時間ts變化的。需要指出的是，雖然式(13)中并未明確寫出目標的多普勒頻率，但實際上目標的多普勒信息蘊含在式(13)的指數項中。

2.2 似然函數

為便于似然函數的推導，首先定義如下向量：

(17)

(18)

(19)

(20)

則式(12)中的脈沖壓縮信號可表示為：

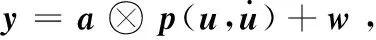
(21)

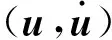
(22)

這里需要指出的是，式(22)中忽略了與估計問題無關的常數項。為了消除冗余參數a，對式(22)關于a求偏導，并令偏導為零，從而得到a的最大似然估計為：

(23)

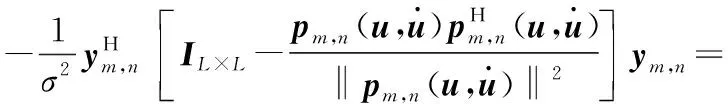
(24)

(25)

3 克拉美羅界分析

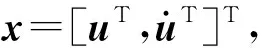
(26)

式中，分塊子矩陣Jx,x，Jx,γ，Jγ*,x，Jγ*,γ的定義為：

(27)

式中，h,f?θ，l(y|θ)為式(22)中的對數似然函數。

CRLB等于Fisher信息矩陣的逆，即：

CRLB(θ)=FIM(θ)-1，

(28)

根據向量θ的構成，目標位置-速度估計CRLB對應于CRLB(θ)左上角6×6的分塊子矩陣。利用分塊矩陣求逆定理，可得目標位置-速度估計CRLB為：

(29)

借助如下中間變量：

(30)

則利用鏈式求導法則，可將式(29)進一步表示為：

(31)

(32)

(33)

根據式(27)，得到矩陣Jτ,τ，Jτ,γ，Jγ*,τ，Jγ,γ具體為：

(34)

(35)

Jτ,γ=(Jγ,τ)T,Jγ*,τ=(Jγ,τ)*，

(36)

(37)

式中，

(38)

式中，W為離散傅里葉變換矩陣；diag(βi,j)表示以βi,j為對角元素的MN×MN對角矩陣。

4 仿真結果分析

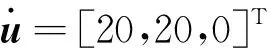
算法的定位誤差性能用1 000次蒙特卡羅仿真的均方根誤差(Root Mean Square Error, RMSE)定量衡量：

(39)

(40)

首先，為了直觀展示本文算法的有效性，利用本文算法對接收信號進行處理。圖2給出了本文算法積累出的目標位置和速度估計的似然函數圖。

圖2 目標直接定位似然函數圖Fig.2 Likelihood function for direct position determination of target

從圖2可以看出，原本非常微弱的目標回波信號在其真實位置參數處得到峰值，并且得益于觀測時間內的長時間信號能量積累，原本淹沒在噪聲中的目標回波信號積累的峰值遠高于周圍噪聲。通過搜索目標似然函數峰值的對應目標位置-速度參數，即可得到目標位置-速度估計。

接下來，為了展示算法對目標位置-速度的估計效果，在同樣的仿真條件下，利用算法進行1 000次蒙特卡羅仿真定位，其估計結果的散點分布如圖 3所示。

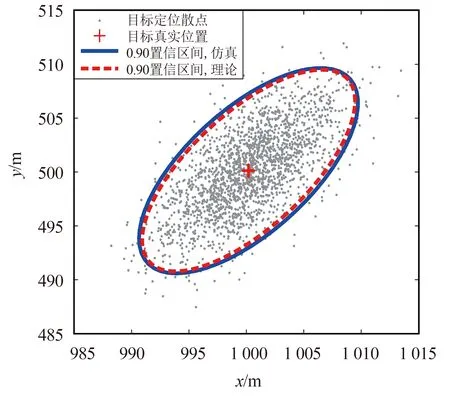
(a)位置估計

(b)速度估計圖3 目標定位散點圖Fig.3 Scatter diagram for target localization

圖3展示了本文算法多次獨立定位結果的散點圖。其中，藍色橢圓為仿真定位估計誤差的90%置信區間，由1 000次蒙特卡羅結果計算得出；紅色橢圓為第4節中CRLB預測的90%置信區間。顯然，理論預測和仿真實驗得到的置信區間幾乎相同，這表明本文算法在一定信號條件下的定位誤差可以達到CRLB。

在實際的目標定位場景中，受到目標散射面積等因素的影響，目標回波的功率強弱也有不同。為了更全面地評估本文算法的定位性能，利用本文算法在不同的目標回波信號的功率下進行仿真定位。為了突出本文算法的性能優勢，將文獻[7]中的傳統兩步定位算法和文獻[17]中的直接定位算法作為對比算法，結果如圖 4所示。

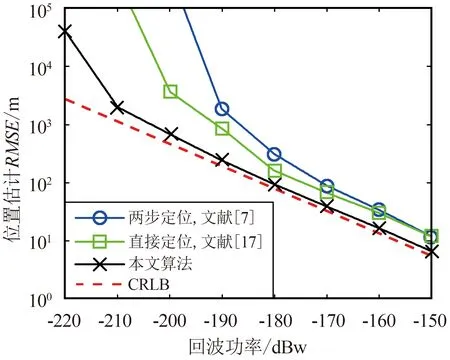
(a)位置估計

(b)速度估計圖4 不同目標回波信號功率下的定位性能Fig.4 Localization performance under different target echo power

從圖 4可以看出，總體上，隨著回波功率的增加，幾種算法的定位誤差均隨之減小。然而，與之前引言部分的介紹一致，文獻[7]中的傳統兩步定位算法由于步間信息損失，定位誤差顯著高于CRLB。文獻[17]中的直接定位算法避免了傳統兩步定位的缺陷，定位精度有所提升，但是由于其沒有利用北斗信號結構已知的特性，定位誤差仍難以達到CRLB。相比之下，本文算法由于利用已知的北斗信號結構重構了純凈直達波信號，理論上定位性能與主動雷達相當。仿真結果也證明，本文算法在回波功率較高時可以達到CRLB。雖然在回波功率過低時，本文算法的定位誤差也會出現偏離CRLB的“閾值”現象，但是相比于對比算法，本文算法的“閾值”更高，并且偏離CRLB的程度更小。

理論上，目標回波信號的積累時間越長，定位誤差越小。為了評估積累時間對算法定位性能的影響，利用算法在不同積累時間下進行定位。結果如圖 5所示。

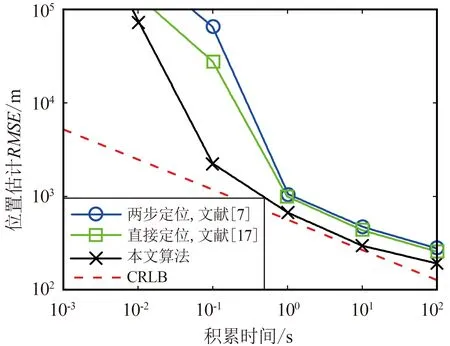
(a)位置估計

(b)速度估計圖5 不同觀測時長下的定位性能Fig.5 Localization performance under different observation time

圖 5給出了不同積累時間下算法的定位誤差。與理論分析一致，隨著積累時間的增加，算法的定位誤差隨之減小。對于本文目標定位場景，本文算法最少只需0.1 s級的積累時間即可實現對目標的有效定位。而2種對比算法則至少需1 s級的積累時間才能實現對目標有效定位。這說明了本文算法利用北斗信號結構重構純凈直達波信號的必要性。需要指出的是，雖然理想情況下延長積累時間可以提高目標定位性能，但是實際中受限于系統計算資源、目標距離徙動和多普勒徙動、目標運動狀態變化等影響，積累時間的延長也受到限制。

5 結論

本文考慮了基于多顆北斗衛星外輻射源的無源雷達目標定位問題，提出了一種聯合北斗衛星信號結構的直接定位算法，推導了目標定位的克拉美羅界，并通過仿真實驗結果驗證了本文算法的有效性和性能優勢。相關結論如下:

① 本文聯合北斗衛星信號結構的直接定位算法的定位性能逼近CRLB，說明了算法的漸近有效性。

② 本文算法的定位精度要優于現有的未利用北斗信號結構的直接定位算法和傳統兩步定位法，定位精度和穩健性顯著提升。

③ 本文算法通過聯合北斗信號結構特性，實現了直達波信號的重構，使得無源雷達的直達波信號不再受噪聲干擾的影響，理論上定位性能可以達到多基地有源雷達的水平。