漸開線齒面串聯(lián)彈性器件傳動機理研究

蔣建東 李明貴 喬 欣

(浙江工業(yè)大學(xué)特種裝備制造與先進加工技術(shù)教育部重點實驗室， 杭州 310023)

0 引言

隨著機器人技術(shù)的發(fā)展，外骨骼機器人在各領(lǐng)域有著廣泛應(yīng)用，在農(nóng)業(yè)領(lǐng)域中，上肢外骨骼可協(xié)助果民采摘果蔬動作，下肢外骨骼則能幫助果民在果園中搬運，可減輕農(nóng)民腰、背部等肌肉的負載[1-5]。關(guān)節(jié)作為外骨骼機器人的重要部件，其結(jié)構(gòu)一直以來都被重點關(guān)注。在傳統(tǒng)機器人關(guān)節(jié)設(shè)計中，為實現(xiàn)精準控制，常對關(guān)節(jié)的傳動性能有很高的要求，而隨著戶外機器人逐漸普及，此類機器人的設(shè)計更偏向輕量化、節(jié)能化，以降低機器人傳動時的啟動功率，PRATT等[6]提出了串聯(lián)彈性驅(qū)動(Series elastic actuators，SEA)結(jié)構(gòu)模型，即在驅(qū)動機構(gòu)與執(zhí)行機構(gòu)之間串聯(lián)一個彈性器件。串聯(lián)彈性驅(qū)動模型提出后，國內(nèi)外學(xué)者相繼對其展開了研究。SEO等[7]提出了一種平面橡膠型的串聯(lián)彈性器件，將驅(qū)動與外圈相連接，負載與內(nèi)圈相連接，外圈與內(nèi)圈之間嵌有4組橡膠，當外圈轉(zhuǎn)動時，壓縮橡膠，橡膠壓縮至能驅(qū)動負載時，內(nèi)圈與負載開始運動實現(xiàn)彈性啟動。LEE等[8]提出的模型中外圈與驅(qū)動相連，內(nèi)圈與負載相連，線性滑塊安裝在外圈上，可在外圈上滑動，內(nèi)圈上安有一個滾輪，滾輪可沿著線性滑塊內(nèi)壁滑動，當外圈開始轉(zhuǎn)動時，線性滑塊相對外圈移動，同時壓縮彈簧，滾輪沿著滑塊內(nèi)壁滑動，從而驅(qū)動內(nèi)圈。

CHAICHAOWARAT等[9]在周轉(zhuǎn)輪系上內(nèi)嵌一個扭簧使其構(gòu)成并聯(lián)彈性驅(qū)動模型，其中扭簧外圈與行星架固定，扭簧內(nèi)圈與機架固定，負載安裝在行星架上，中心輪連接驅(qū)動，當負載正向運動時，儲存一部分能量于扭簧的彈性勢能，用于補充負載反向運動，此模型能儲存部分運動周期的能量在其他運動周期中釋放，更適用于非對稱負載中。

在各種的串聯(lián)彈性驅(qū)動結(jié)構(gòu)中，有兩種結(jié)構(gòu)被更多的學(xué)者采用，一種為文獻[10-14]中的模型，由內(nèi)圈、外圈與3或4組彈簧組成，內(nèi)圈連接驅(qū)動，外圈連接負載，當啟動時由內(nèi)圈開始轉(zhuǎn)動，內(nèi)圈轉(zhuǎn)動壓縮彈簧，當彈簧壓縮一定時，與負載相連的外圈開始轉(zhuǎn)動；另一種為文獻[15-17]中采用的模型，驅(qū)動與負載之間通過彈性的金屬梁相連，當驅(qū)動的內(nèi)圈轉(zhuǎn)動時先拉伸或壓縮彈性梁，彈性梁再拉或推動外圈轉(zhuǎn)動。

串聯(lián)彈性驅(qū)動模型通過彈性傳動啟動，能降低啟動功率而被廣泛應(yīng)用于機器人、外骨骼關(guān)節(jié)處[18-21]，而目前大多數(shù)研究探討了串聯(lián)彈性驅(qū)動模型的彈性啟動過程，其結(jié)構(gòu)共性為內(nèi)圈(或外圈)與驅(qū)動相連，外圈(或內(nèi)圈)與負載相連，外圈、內(nèi)圈之間安有彈性器件如直線圓柱彈簧、扭簧、橡膠等。而此類結(jié)構(gòu)現(xiàn)有兩處不足：由線性彈簧組成的旋轉(zhuǎn)元件，幾何結(jié)構(gòu)差異導(dǎo)致等效轉(zhuǎn)動剛度不恒定，造成轉(zhuǎn)矩與轉(zhuǎn)角呈較差的線性關(guān)系；彈性傳動結(jié)束后彈性器件被壓縮至極限后沒有良好的過渡環(huán)節(jié)。針對上述不足，本文提出一種啟動時采用彈性傳動，當負載較大時，則轉(zhuǎn)換成剛性傳動的傳動方案，從而保留彈性傳動的軟啟動特性，又擴大傳動負載范圍、提高傳動的穩(wěn)定性。

1 漸開線齒面彈性器件結(jié)構(gòu)設(shè)計

1.1 漸開線齒面彈性器件結(jié)構(gòu)與傳動原理

漸開線齒面彈性器件(齒面彈性器件)由內(nèi)圈、彈簧與外圈構(gòu)成，內(nèi)圈與外圈通過3根彈簧相連接。齒面彈性器件的傳動可分為彈性傳動、齒面嚙合與剛性傳動階段。在彈性傳動中，主動件內(nèi)圈轉(zhuǎn)動，逐漸壓縮彈簧，彈簧彈力作用于外圈，當彈簧力能驅(qū)動執(zhí)行機構(gòu)外圈運動時，齒面彈性器件將通過彈簧將內(nèi)圈的轉(zhuǎn)動傳動至外圈，實現(xiàn)彈性傳動；而齒面嚙合階段是內(nèi)圈轉(zhuǎn)動至與外圈接合時，由于內(nèi)外圈軸心裝配偏差，使得內(nèi)外圈通過內(nèi)齒輪嚙合方式傳動；當嚙合階段結(jié)束后，則內(nèi)外圈將通過接觸的方式實現(xiàn)剛性傳動。

1.2 彈性傳動受力分析

圖1為齒面彈性器件彈性傳動單根彈簧受力分析圖，將彈簧力看作作用在彈簧中心線上的集中力，彈簧中心線與圓心距離為RS、與豎直方向傾角為θS(彈簧安裝傾角)，啟動時彈簧初始長度為l0，隨著主動內(nèi)圈相對外圈轉(zhuǎn)動φ時，彈簧逐漸被壓縮至l，依據(jù)幾何關(guān)系，可得

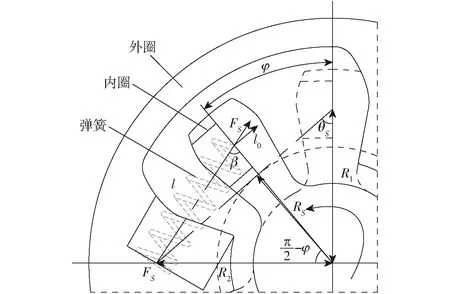
圖1 彈性傳動單根彈簧受力分析Fig.1 Mechanic analysis on elastic drive single spring

(1)

式中R1——內(nèi)圈彈簧安裝位置，mm

R2——外圈彈簧安裝位置，mm

k——彈簧剛度，取1.36 N/mm

β——彈簧與內(nèi)圈夾角，rad

FS——彈簧力，N

T——轉(zhuǎn)矩，N·mm

通過式(1)可知，在彈性傳動中，轉(zhuǎn)矩T與相對轉(zhuǎn)角φ的關(guān)系為

(2)

為使得彈性傳動中轉(zhuǎn)矩與轉(zhuǎn)角更具有線性關(guān)系，以降低彈性傳動的頓挫感，提出轉(zhuǎn)動剛度變化率δK，表示轉(zhuǎn)動剛度相對變化程度，計算式為

(3)

其中

式中K——轉(zhuǎn)動剛度，N·mm/rad

Kmean——平均轉(zhuǎn)動剛度，N·mm/rad

轉(zhuǎn)動剛度變化率δK∈[0,+∞)，當δK=0時，表示轉(zhuǎn)動剛度為恒定不變的常數(shù)，當δK越大時，表示轉(zhuǎn)動剛度變化程度越大，彈性傳動過程中頓挫感越強。

由式(2)與式(3)可知，彈簧產(chǎn)生的轉(zhuǎn)矩T與彈簧剛度k成正比，與彈簧離圓心距離RS的平方成正比，而對于轉(zhuǎn)動剛度K，k與RS僅作為一個比例增益，故轉(zhuǎn)動剛度變化率δK僅與彈簧切線傾角θS有關(guān)。

圖2為轉(zhuǎn)動剛度變化率與彈簧切線傾角曲線，其中理論曲線由式(2)與式(3)得出，仿真數(shù)據(jù)通過不同傾角模型進行ADAMS動力學(xué)仿真得出(受模型尺寸限制，不考慮彈簧傾角過大或過小情況)。可以看出，轉(zhuǎn)動剛度變化率以彈簧傾角θS=π/4對稱，當傾角為π/4±1.337 85 rad時，轉(zhuǎn)動剛度變化率為最小0.117 57。

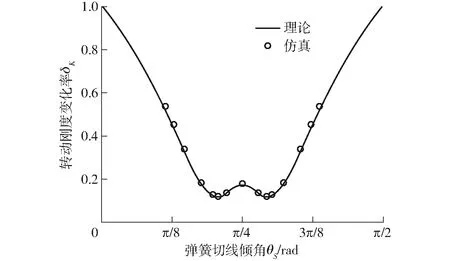
圖2 轉(zhuǎn)動剛度變化率與彈簧傾角理論與仿真曲線Fig.2 Theoretical and simulation curves of rotational stiffness rate of change and spring inclination

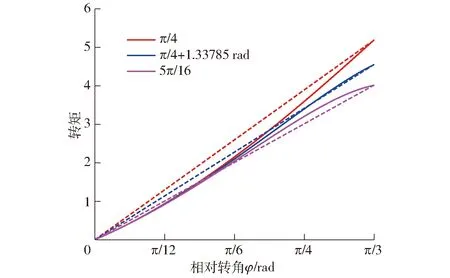
圖3 不同彈簧傾角的轉(zhuǎn)矩啟動曲線Fig.3 Spring torque starting curves for different spring inclination angles

1.3 齒面嚙合滑動率分析

為降低從彈性傳動到剛性傳動轉(zhuǎn)換的沖擊影響，在內(nèi)圈接觸面設(shè)有外漸開線齒廓，在外圈接觸面設(shè)有內(nèi)漸開線齒廓，使得在彈性傳動與剛性傳動之間增加一個齒面內(nèi)嚙合過程。

在漸開線齒廓嚙合過程中，嚙合接觸點的相對滑動越大，則齒面磨損越嚴重，更容易發(fā)生膠合破壞[22]。圖4為齒面內(nèi)嚙合過程，lO1O2為內(nèi)外圈的軸心裝配偏差，γ12為內(nèi)外圈的軸心偏差角(偏角，圖4中∠xO2O1)，嚙合線同時與內(nèi)圈基圓、外圈基圓相切，且切點分別為N1、N2，嚙合點為點K，嚙合起點B2為嚙合線與內(nèi)漸開線齒廓的交點，嚙合過程接觸終點B1為嚙合線與內(nèi)圈齒頂圓的交點，內(nèi)漸開線與內(nèi)圈基圓相交且始于點A。嚙合線同時與內(nèi)外基圓相切，故O1O2與N1N2平行，長度相等。

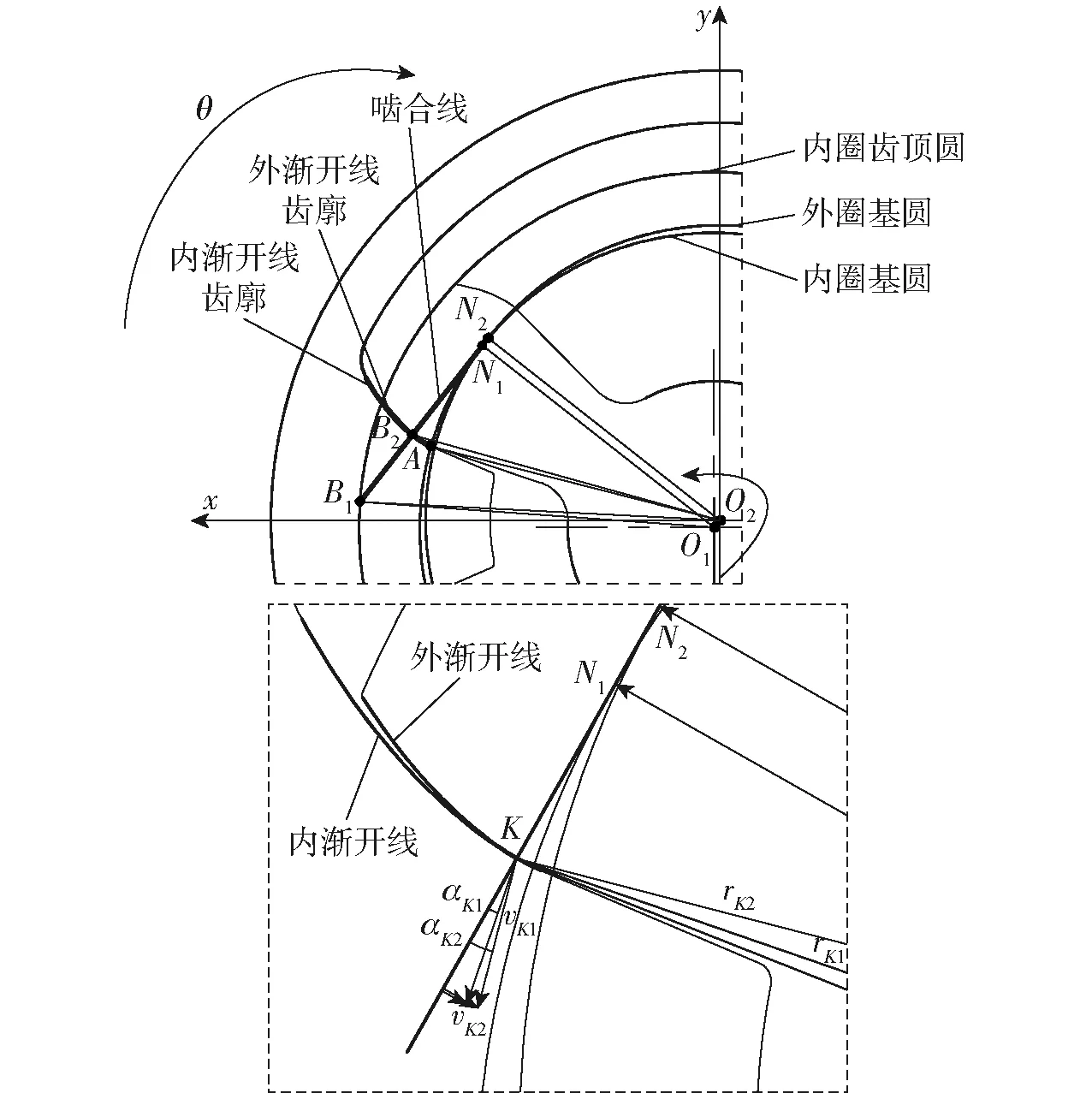
圖4 齒面嚙合過程Fig.4 Tooth surface meshing process

漸開線齒廓嚙合過程中，滑動率為嚙合點處的相對滑動速度與切向速度比，根據(jù)嚙合過程的幾何關(guān)系，內(nèi)圈滑動率η1為

(4)

式中vt1、vt2——內(nèi)、外圈嚙合點切向速度，mm/s

vK1、vK2——內(nèi)、外圈嚙合點線速度，mm/s

αK1、αK2——內(nèi)、外圈嚙合點壓力角，rad

rK1、rK2——嚙合點距內(nèi)、外圈中心長，mm

ω1、ω2——內(nèi)、外圈角速度，rad/s

齒面彈性器件內(nèi)外圈嚙合傳動比為1，當內(nèi)外圈存在軸心裝配偏差時，根據(jù)漸開線中心距可分性[23]，其傳動比在嚙合過程中保持不變，即ω1=ω2不會因為存在偏差而改變，故內(nèi)圈滑動率η1為

(5)

同理，可以得出外圈滑動率η2為

(6)

結(jié)合式(5)、(6)與圖4可知，內(nèi)外圈的滑動率與偏差成正比，嚙合點K在B1B2中移動，故當安裝位置確定后，嚙合過程中最大滑動率ηmax發(fā)生在嚙合起點B2處，即

(7)

嚙合起始點B2直接影響著齒面嚙合傳動的最大滑動率，分析其具體位置(圖4)，以外圈圓心為中心，建立直角坐標系與極坐標系，x軸順時針旋轉(zhuǎn)為極角θ增大方向，Ox為極軸，極徑為ρ，則由漸開線函數(shù)與幾何關(guān)系可知

(8)

式中rb——內(nèi)外圈基圓半徑，取28.19 mm

θA——內(nèi)漸開線起點極角(∠AO2x),取0.016 4 rad

γ12——軸心偏差角

齒面彈性器件為3組周向均勻分布的“內(nèi)齒”嚙合，故只需討論γ12為0～π/3，當γ12>π/3時，嚙合起始點將在點A以下，齒面滑動將從點A開始，滑動率將與γ12=π/3一致。從式(8)可得最大滑動率與內(nèi)外圈軸心裝配偏差的關(guān)系如圖5所示。

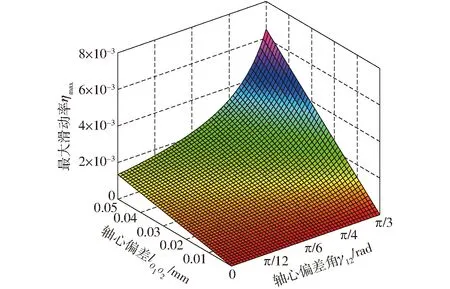
圖5 最大滑動率與軸心裝配偏差關(guān)系Fig.5 Relationship between maximum slip rate and axis assembly deviation

由圖5可知，內(nèi)外圈的安裝偏差與偏差角均會影響嚙合過程的最大滑動率，當內(nèi)外圈軸心無偏差時，最大滑動率為0，即無滑動，而由于內(nèi)外圈需要相對轉(zhuǎn)動，在安裝過程中將不可避免地造成軸心裝配偏差。在內(nèi)外圈安裝偏差小于0.05 mm時，齒面嚙合過程中最大滑動率為0.006 5。

2 齒面彈性器件仿真

采用最佳彈簧安裝傾角結(jié)構(gòu)對齒面彈性器件進行ADAMS仿真，仿真模型結(jié)構(gòu)參數(shù)如表1所示。

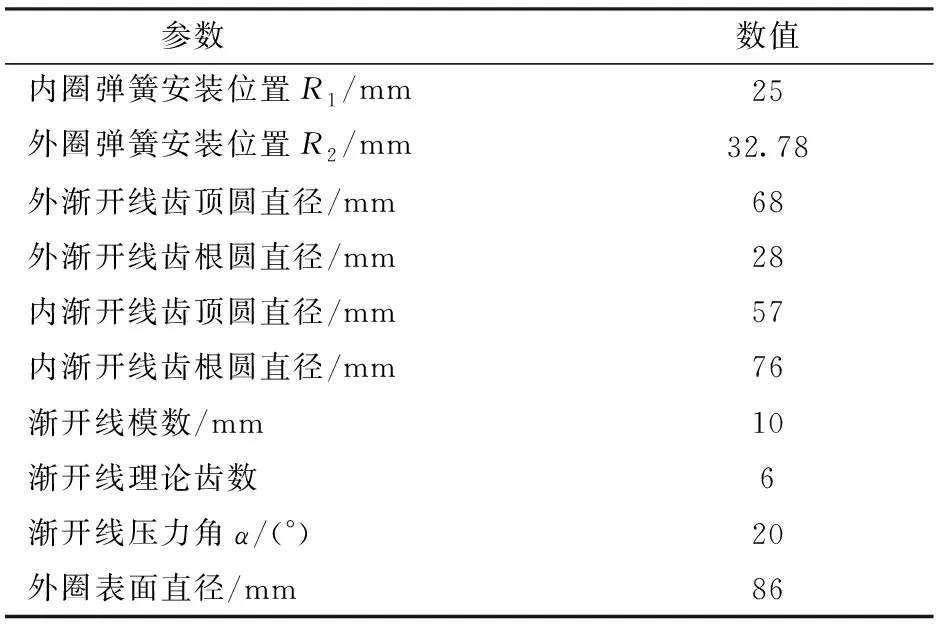
表1 仿真模型結(jié)構(gòu)參數(shù)Tab.1 Structural dimensions of simulation model

圖6為齒面彈性器件仿真模型，為研究漸開線齒面接合對傳動力矩的影響，設(shè)置平面矩形對照組作為對比。內(nèi)圈與外圈通過彈簧連接，彈簧參數(shù)設(shè)置為彈性系數(shù)1.36 N/mm、圈數(shù)12、直徑 10 mm；內(nèi)圈與外圈分別對大地添加轉(zhuǎn)動副，并設(shè)置內(nèi)圈為主動件，添加轉(zhuǎn)動驅(qū)動，且將外圈與大地的轉(zhuǎn)動副添加轉(zhuǎn)動摩擦力，通過設(shè)置轉(zhuǎn)動摩擦預(yù)載荷構(gòu)造外圈負載；考慮后續(xù)將以3D打印進行進一步實驗驗證，故仿真的接觸力參考尼龍材料接觸設(shè)置。

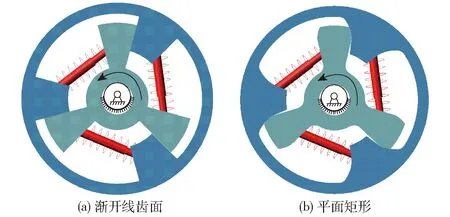
圖6 齒面彈性器件仿真模型Fig.6 Simulation model of tooth surface elastic device

圖7為內(nèi)外圈軸心偏差角為π/3時不同轉(zhuǎn)矩曲線，在傳動的彈性過程中，轉(zhuǎn)矩隨時間呈近似線性增大；隨后內(nèi)圈與外圈接觸，然后含有漸開線齒面的彈性器件進行齒面嚙合過程，而平面矩形則是一個沖擊，在內(nèi)外圈剛接觸時，轉(zhuǎn)矩會激增，從圖7可以看出，在偏差角π/3下軸心偏差在0.05 mm內(nèi)，設(shè)有漸開線齒面的齒面彈性器件沖擊轉(zhuǎn)矩均小于平面矩形組；在齒面嚙合過程結(jié)束后，傳動則轉(zhuǎn)為剛性傳動，轉(zhuǎn)矩與負載相等且保持不變。在此結(jié)構(gòu)模型下，通過式(2)可知，齒面彈性器件傳動從彈性啟動到剛性傳動的臨界轉(zhuǎn)矩為2 446.13 N·mm。

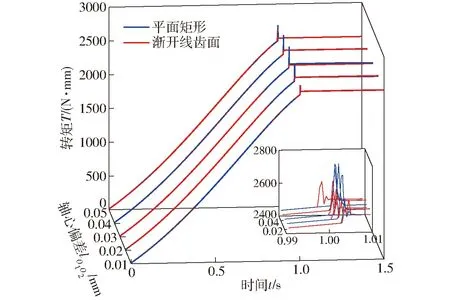
圖7 偏差角為π/3時啟動轉(zhuǎn)矩仿真曲線Fig.7 Simulation curves of starting torque when deflection angle was π/3

可依據(jù)不同負載場合選用合適彈性系數(shù)的彈簧來提高傳動性能。

以傳動過程沖擊產(chǎn)生的最大轉(zhuǎn)矩減去恢復(fù)穩(wěn)定傳動后的轉(zhuǎn)矩(勻速轉(zhuǎn)動下的負載)為轉(zhuǎn)矩激增值，表2為平面矩形對照關(guān)節(jié)轉(zhuǎn)矩激增值，表3為漸開線齒面彈性器件的轉(zhuǎn)矩激增值。

表2 平面矩形模型轉(zhuǎn)矩激增值Tab.2 Torque excitation value of plane rectangular model N·mm

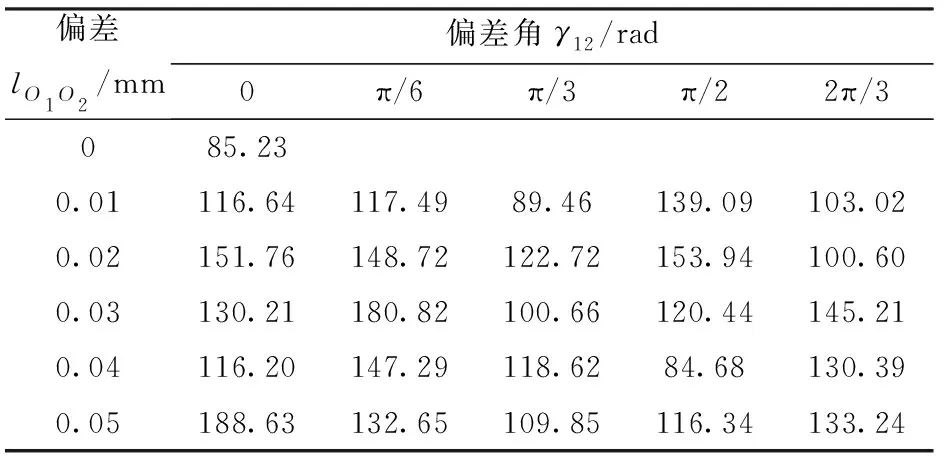
表3 漸開線齒面模型轉(zhuǎn)矩激增值Tab.3 Torque excitation value of involute tooth surface model N·mm

由表2、3可知，在內(nèi)外圈理想安裝中心無偏差時，漸開線齒面模型與平面矩形模型的轉(zhuǎn)矩激增值相差不大，結(jié)合圖4，此時嚙合線長度為0，即無嚙合過程，內(nèi)漸開線曲面與外漸開線曲面完全貼合，平面矩形模型通過平面實現(xiàn)面接觸，故兩種模型均通過面接觸傳動；當內(nèi)外圈中心出現(xiàn)偏差時，漸開線齒面模型激增轉(zhuǎn)矩小于平面矩形模型激增轉(zhuǎn)矩，平均減小43.55%，原因為一旦內(nèi)外圈中心出現(xiàn)偏差，平面矩形模型接觸將從原來的面接觸變?yōu)榫€接觸，而漸開線齒面模型則有一個內(nèi)齒嚙合過程過渡(圖8)，嚙合點從齒根處滑移至齒頂處，嚙合過程中同時使外圈轉(zhuǎn)動，減小內(nèi)外圈直接碰撞的剛性沖擊，從而減小內(nèi)外圈沖擊造成的轉(zhuǎn)矩激增。

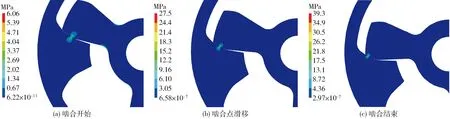
圖8 嚙合過程仿真應(yīng)力分布Fig.8 Meshing process simulation stress distribution

圖9為網(wǎng)格尺寸為0.5 mm的有限元仿真與理論分析(圖4)的嚙合軌跡對比，仿真的嚙合點分布在理論嚙合線B2B1附近，且均在最小網(wǎng)格單元之間。

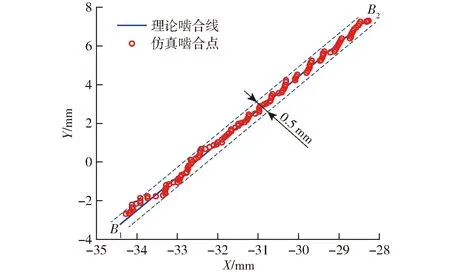
圖9 仿真與理論嚙合軌跡Fig.9 Simulation and theoretical meshing trajectory

3 齒面彈性器件實驗

齒面彈性器件可應(yīng)用于搬運助力外骨骼機器人的關(guān)節(jié)(圖10)，安裝在減速器與負載之間，內(nèi)圈與減速器輸出軸相連，外圈與負載相連，實驗的齒面彈性器件模型各結(jié)構(gòu)尺寸與仿真模型一致(表1)，采用3D打印制造，材料為白色尼龍(FS3300PA)，材料機械性能：拉伸強度46 MPa、拉伸模量1 602 MPa、彎曲強度46.3 MPa、彎曲模量1 300 MPa，彈簧參數(shù)為：線徑1 mm、直徑10 mm、彈性系數(shù)1.36 N/mm。

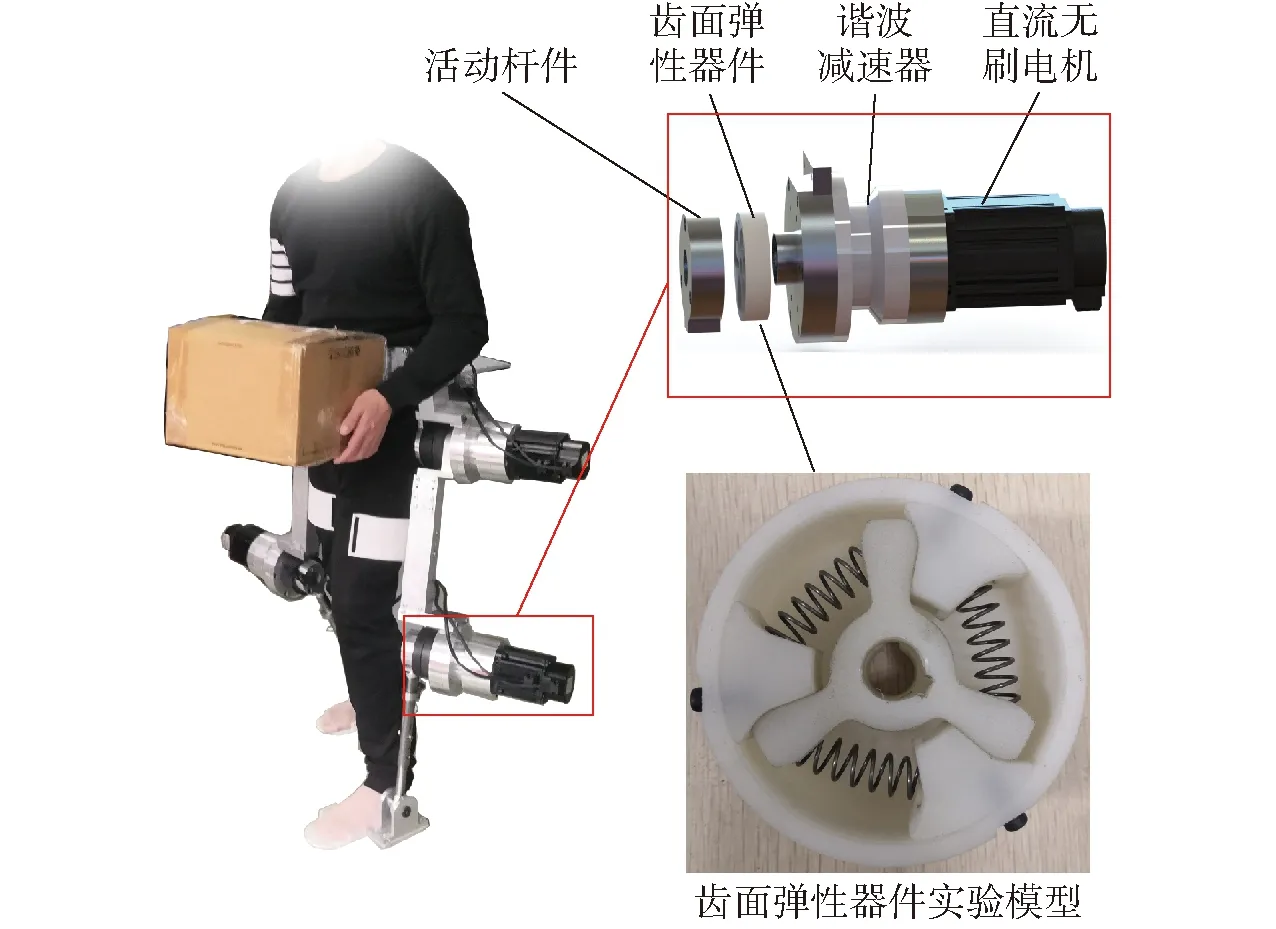
圖10 齒面彈性器件及其應(yīng)用Fig.10 Tooth surface elastic device and its application

實驗平臺如圖11所示，主要由變頻電機(YP-50-055-4型)、轉(zhuǎn)矩轉(zhuǎn)速傳感器1(JN338A-10A型)、齒面彈性器件、轉(zhuǎn)矩轉(zhuǎn)速傳感器2(JN338A-50A型)、磁粉制動器(DZF-5型)組成。齒面彈性器件輸入軸與轉(zhuǎn)矩轉(zhuǎn)速傳感器1相連，輸出軸與轉(zhuǎn)矩轉(zhuǎn)速傳感器2相連，變頻電機作為驅(qū)動提供輸入動力，磁粉制動器提供負載。實驗過程為：設(shè)置電機輸入使得每組實驗的輸入(轉(zhuǎn)矩轉(zhuǎn)速傳感器1)轉(zhuǎn)速一致，調(diào)節(jié)磁粉制動器，記錄不同負載下的轉(zhuǎn)矩啟動數(shù)據(jù)。

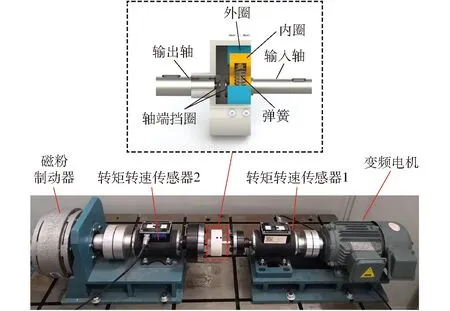
圖11 齒面彈性器件實驗臺Fig.11 Tooth surface elastic device test bench

圖12為不同負載下實驗與仿真的轉(zhuǎn)矩啟動曲線，可以看出實驗與仿真的轉(zhuǎn)矩曲線趨勢一致，均有彈性啟動過程；但在相同負載下，實驗轉(zhuǎn)矩均大于仿真轉(zhuǎn)矩，這使得實驗的彈性啟動更長，實驗轉(zhuǎn)矩平均比仿真轉(zhuǎn)矩大277.58 N·mm，原因為實驗傳動過程中磁粉制動器、轉(zhuǎn)矩轉(zhuǎn)速傳感器等含有一定的摩擦阻力，造成實際負載比設(shè)定負載偏大。

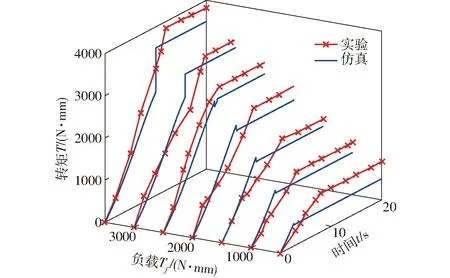
圖12 實驗與仿真轉(zhuǎn)矩曲線Fig.12 Experiment and simulation torque curves

由圖12可知，隨著負載的增大，實驗轉(zhuǎn)矩與仿真轉(zhuǎn)矩的偏差存在先減小后增大趨勢，其原因為：當負載Tf≤1 000 N·mm時，摩擦阻力對傳動力矩占比較大，導(dǎo)致實驗測得轉(zhuǎn)矩較仿真偏差較大；隨著負載的增加，摩擦阻力對傳動力矩的占比逐漸減小，實驗與仿真的偏差減小；而當負載增至Tf≥2 000 N·mm時，齒面彈性器件驅(qū)動此負載內(nèi)外圈貼合后未能立即驅(qū)動，負載過大內(nèi)外圈產(chǎn)生一定的變形后傳動，傳動力矩有一部分作用在器件本身，導(dǎo)致實驗測得轉(zhuǎn)矩與理論偏差較大。

表4為不同負載實驗下的齒面彈性器件的傳動效率，隨著負載的增大傳動效率逐漸增大，在負載較小時，內(nèi)圈僅壓縮了部分彈簧，外圈即可發(fā)生轉(zhuǎn)動，此時內(nèi)圈與外圈并沒接觸，完全通過彈簧進行彈性傳動，傳動穩(wěn)定性與效率較低；在負載較大時，內(nèi)圈壓縮彈簧，還不足以驅(qū)動負載，內(nèi)圈與負載剛接觸時首先通過齒面嚙合傳動，嚙合結(jié)束后進入剛性傳動階段，傳動穩(wěn)定性與效率較高。

表4 不同負載的傳動效率Tab.4 Transmission efficiency of different loads

4 結(jié)論

(1)齒面彈性器件的轉(zhuǎn)動剛度和彈簧中心線與圓心距離的平方成正比，與彈簧剛度成正比，而轉(zhuǎn)動剛度變化率與彈簧安裝傾角有關(guān)，即通過改變齒面彈性器件結(jié)構(gòu)尺寸與彈簧剛度來改變轉(zhuǎn)動剛度，通過改變彈簧安裝傾角，來降低轉(zhuǎn)動剛度變化率，當安裝傾角為π/4±1.337 85 rad時，轉(zhuǎn)動剛度變化率最小。

(2)齒面嚙合的最大滑動率受齒面彈性器件軸心裝配偏差影響，當偏角一定時，最大滑動率與軸心裝配偏差成正比，當軸心裝配偏差在0.05 mm內(nèi)時，最大滑動率為0.006 5。

(3)在彈性傳動與剛性傳動轉(zhuǎn)換時，傳動轉(zhuǎn)矩會發(fā)生一個激增現(xiàn)象，內(nèi)外圈的軸心裝配偏差使得轉(zhuǎn)矩激增更大，采用漸開線齒面嚙合過渡，利用漸開線齒廓中心距的可分性在嚙合的同時使內(nèi)外圈等角速度轉(zhuǎn)動，當軸心偏差在0.05 mm內(nèi)時，較平面模型轉(zhuǎn)矩激增值平均降低43.55%。