水下結構激振力與輻射聲壓關系的驗證
王永富
(中國人民解放軍海軍91970部隊,遼寧大連 116041)
0 引言
在研究水下結構的振動和聲輻射時,不可避免會涉及流固耦合問題,對流固耦合規律的認識程度是實現對水下結構振動和聲輻射預報的關鍵。文獻[1]、文獻[2]分別闡述了聲學和流體力學的基本原理,文獻[3]研究了有限元的聲輻射,文獻[4]、文獻[5]則提出附加阻尼質量法,采用FORTRAN 代碼計算外域流體附加質量和附加阻尼矩陣,采用結構有限元分析程序對結構和內域流體作有限元分析,采用DMAP 代碼將附加質量和附加阻尼同結構質量矩陣和阻尼矩陣相疊加,實現了流固耦合計算。文獻[6]依據不同域的特點,結構和流體內域采用有限元方法、流體外域采用邊界元法,研發了計算水下大型結構流固耦合振動和聲輻射的計算程序。一些學者認為水中結構流固耦合振動及其聲輻射是一個非線性問題,然而大多數研究這一問題的文章均采用線性方程進行求解。本文著重對小振幅振動時的流固耦合系統進行研究,對激振力和輻射聲壓的關系進行數值和試驗驗證,深化對水下結構耦合振動規律的認識。
1 基本理論
結構在流體中振動時,本質上就是結構振動和流體的耦合。忽略介質對聲波的粘性吸收,假定介質為均勻的理想流體,略去介質的熱傳導作用,考慮介質中傳播的是小振幅波。在定解條件:固體壁面上的邊界條件、有界條件、輻射條件下,由這些條件可以得到以速度勢φ 控制的方程如下[5]。
式(1)是一個關于速度勢φ 的線性定解問題,所以其描述的結構與流體耦合振動所組成的是一個線性系統。
2 試驗驗證及數值仿真
2.1 試驗模型介紹
制造了一個加肋圓柱殼,在圓柱殼內部設計了基座和9 條等間距分布肋骨,在基座上方安裝激振機(圖1~圖2)。其中,圓柱殼長1000 mm、直徑800 mm,肋骨尺寸5 mm×25 mm,肋骨間距100 mm;基座面板375 mm×200 mm,端蓋、殼體厚度分別為10 mm、3 mm;所用材料密度為7.85×10-9N/mm3,楊氏模量為206 000 N/mm2,阻尼、泊松比分別為0.06 和0.3。

圖1 加肋圓柱殼模型

圖2 基座及激振機布置
2.2 模型水下布置
對于水下結構聲輻射的測量,比較理想的環境是消聲水池或開闊的湖泊。本次試驗是在某水庫中進行,背景噪聲較低,是比較好的聲場環境。用壓載鐵對圓柱殼進行壓載,并用軟繩連接至雙體船使圓柱殼在處于懸浮狀態。模型水下布置見圖3:圓柱殼軸線距離水面5 m(Z),水聽器距離模型中心6.8 m(r)。在試驗船的首部和左舷放置水聽器(圖4)。
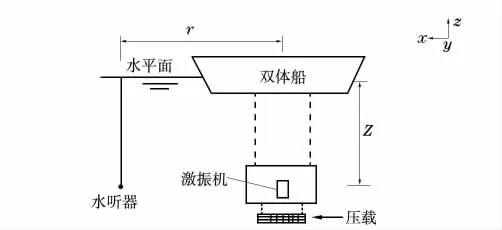
圖3 試驗模型水下布置
2.3 數值仿真
(1)對圓柱殼模型進行數值仿真,采用結構有限元耦合流體邊界元方法并利用有限元軟件PATRAN/NASTAN計算水下結構振動與聲輻射[6],在指定激振頻率下計算不同激振力幅值時的輻射聲壓。
(2)有限元網格見圖5,在基座面板施加垂向激振力F(圖6),數值計算采用的圓柱殼模型材料屬性見上文。

圖5 模型有限元網格
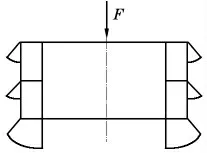
圖6 激振力示意
(3)流體密度ρ 為1020 kg/m3,流體中聲速c 為1450 m/s。
(4)模型放置的位置和聲場計算點與試驗狀態完全相同(圖3、圖4)。

圖4 水聽器布置
2.4 數值仿真與試驗結果對比
試驗時,在指定激振頻率下通過改變激振力的幅值得到對應狀態下的輻射聲壓。圖7 和圖8 分別是激振頻率為128 Hz 和155 Hz 時激振力與輻射聲壓響應曲線。由圖可知,試驗測得1#和2#水聽器的激振力輻射聲壓關系曲線基本符合線性關系。數值計算結果同樣表明激振力與輻射聲壓符合線性關系。
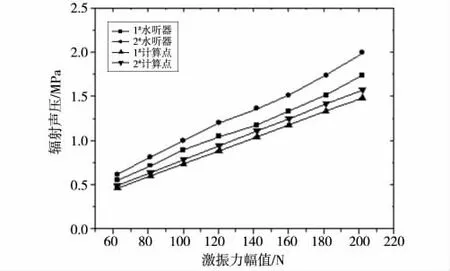
圖7 128 Hz 激振頻率下激振力與輻射聲壓關系
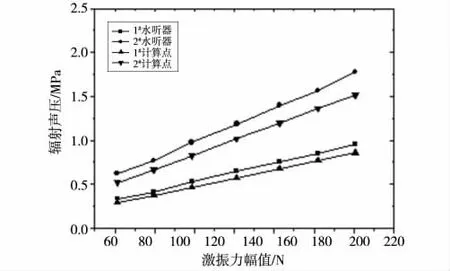
圖8 155 Hz 激振頻率下激振力與輻射聲壓關系
對比數值計算和試驗測得的輻射聲壓值,換算為輻射聲壓級后最大不超過6 dB,導致這種誤差的因素主要有圓柱殼建造焊接過程中的工藝對阻尼因子的影響、水中背景噪聲的影響等。
上述結果表明,激振力和輻射聲壓是線性關系,從而驗證了理論分析的結果。
3 結論
本文通過水下加肋圓柱殼振動與噪聲試驗,并采用有限元耦合流體邊界元法進行了數值仿真及聲輻射計算,結果表明,在指定激振頻率下激振力和輻射聲壓呈很好的線性關系,驗證了小振幅振動時殼體結構與流體耦合振動所組成的是一個線性系統這一理論。

