包含無效點濾波的彈道高度預測

徐瑞辰，牛蘭杰，2，張 珂，2

(1.西安機電信息技術研究所，陜西 西安 710065；2.機電動態控制重點實驗室，陜西 西安 710065)

0 引言

近炸引信對現代武器系統的作戰效能具有重要作用，而彈道高度的測量精度是影響近炸引信最佳炸點起爆的重要因素。目前典型近炸引信，如無線電引信、光學引信的彈道高度測量精度要求一般小于3 m，美軍部分引信炸點控制精度小于1 m，因此提高彈道高度測量精度具有重要實用意義。

近年來，國內外學者開展了在不降低目標檢測概率前提下，提升測量數據更新速率、降低彈道環境噪聲引起的隨機誤差，進而提高測距精度的研究。文獻[1—7]分別用最小二乘法或矩陣加權等方法，提出了不同形式的融合卡爾曼濾波器，用于降低信號發生丟失時的預測誤差。文獻[8—10]研究了利用最小二乘法、內插外推算法、三次樣條插值、RBF神經網絡等改變測量數據更新速率以進行時間對準的方法，但計算復雜度和樣本量需求高、抗干擾能力弱，難以在彈載平臺使用。文獻[11]在研究異步信號融合系統時利用偽測量原理，通過對高數據更新速率的傳感器數據進行最小二乘估計，用量測估計值代替量測真值，調整數據更新速率，將異步數據融合轉化為同步數據融合，然而此方法僅限用于均速運動模型，適用面窄，不適用于機動性較強的彈藥平臺。文獻[12—13]分別通過建立不同采樣時刻下的狀態空間模型，利用融合遞歸的方式進行異步融合。此外，文獻[14—17]研究了基于偽測量法或序貫融合法的異步融合技術，可用于改變信息更新速率。

綜上所述，改變信號采樣間隔、提高探測精度的算法已較為成熟，經典的方法有多點插值法、狀態空間分解法、偽測量法和新興的神經網絡算法等，其中異步信號融合系統中常用的卡爾曼濾波算法和偽測量法具有濾波精度高等優點，但是由于引信在對地彈道高度測量時，具有處理速度高、實時性強等特點，傳統基于偽測量技術的卡爾曼濾波算法包含大量矩陣求逆運算，難以滿足彈上環境對計算量的要求。本文針對彈載使用平臺，以減小計算量和實現高度預測為目標，提出無效點概念，將探測漏點、干擾點、需插值點設置為兩種類型的無效點，將無效點和額外預測點利用系統狀態方程、擴展卡爾曼濾波、偽測量技術等處理算法進行濾波和更新，進行彈道高度預測，達到降低測量誤差、降低采樣間隔的效果。

1 高度預測算法

1.1 卡爾曼濾波算法

卡爾曼濾波算法在彈藥制導、防空雷達航跡預測等場景中得到廣泛使用，可以預測運動目標軌跡，特別是在信號受到干擾或者測量精度不夠時能夠有效避免因信號丟失、測量精度低、受環境噪聲干擾等原因導致的測量數據失效問題。

本文采用的卡爾曼濾波算法根據目標之前的運動狀態推算下一步運動狀態，可以降低測量誤差，減少隨機噪聲影響，并預測后續運動狀態，而且僅利用已知歷史信息即可進行實時計算，具有計算實時性強等特點。

1.1.1預測與更新流程

卡爾曼濾波(Kalman filter, KF)是最優估計理論之一，用于遞推系統狀態的最小方差線性無偏估計，能估計下一步狀態和下一步誤差協方差。

在不考慮控制輸入量的情況下，卡爾曼濾波的線性、離散系統方程和測量方程分別如下：

xk=Φk|k-1xk-1+Γk|k-1wk-1,

(1)

zk=Hkxk+vk,

(2)

式中，xk為系統的狀態向量，zk為可以實際測量的量(觀測向量)，Φk|k-1為狀態轉移矩陣，Γk|k-1為過程噪聲分布矩陣，Hk為觀測矩陣，wk-1為過程噪聲，vk為測量噪聲，二者都是均值為零高斯白噪聲，且互不相關。過程噪聲協方差為Qk(非負陣)，測量噪聲協方差為Rk(正定陣)。

1)狀態的一步預測方程為

(3)

2)均方誤差的一步預測方程為

(4)

式(4)中，Pk|k為狀態估計誤差協方差陣。

3)濾波增益權重方程為

(5)

4)濾波估計方程(更新方程)為

(6)

5)誤差協方差更新方程為

Pk|k=[In-KkHk]Pk|k-1。

(7)

將步驟5)得到的結果，代回步驟1)，即可完成全狀態估計。

在對地近炸引信測高使用場景中，同樣可以采用卡爾曼濾波算法對彈道高度進行估計，在存在干擾信號時高度預測效果示意圖如圖1所示。

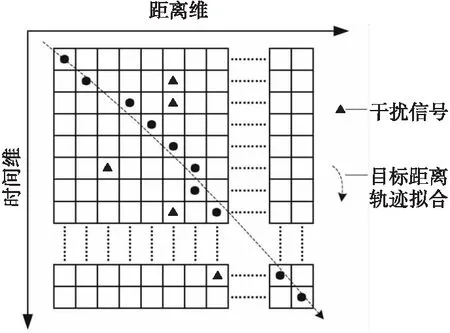
圖1 高度預測效果示意圖Fig.1 Height prediction effect

本文采用卡爾曼濾波算法對高度測量信息在時間-距離維度進行預測，由于卡爾曼濾波算法對非線性航跡適應力不足，且無法完成提高數據更新速率等工作，因此需要做出改進。

1.1.2擴展卡爾曼濾波算法

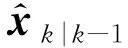
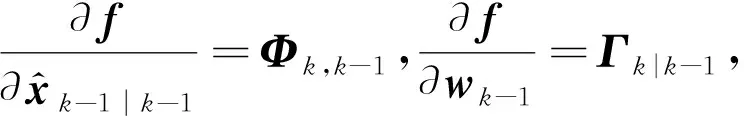
xk≈Φk|k-1xk-1+Γk|k-1wk-1，

(8)

zk≈Hkxk+vk。

(9)

之后即可利用標準卡爾曼濾波方法進行迭代，其中狀態轉移矩陣Φk,k-1和觀測矩陣Hk分別由f(*)和h(*)的雅可比矩陣來替代。

1.2 偽測量法

在近炸引信對地測高過程中往往存在有效量測信息丟失的現象，因此需要通過已確定的量測信息求解在需要量測信息丟失時刻的狀態向量，代替真實量測值，此算法稱為偽測量法。

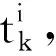
(10)

(11)

為了簡化公式，設

(12)

(13)

則式(11)可以簡化為如下偽測量方程：

(14)

且偽測量的協方差矩陣的完整形式為[16]

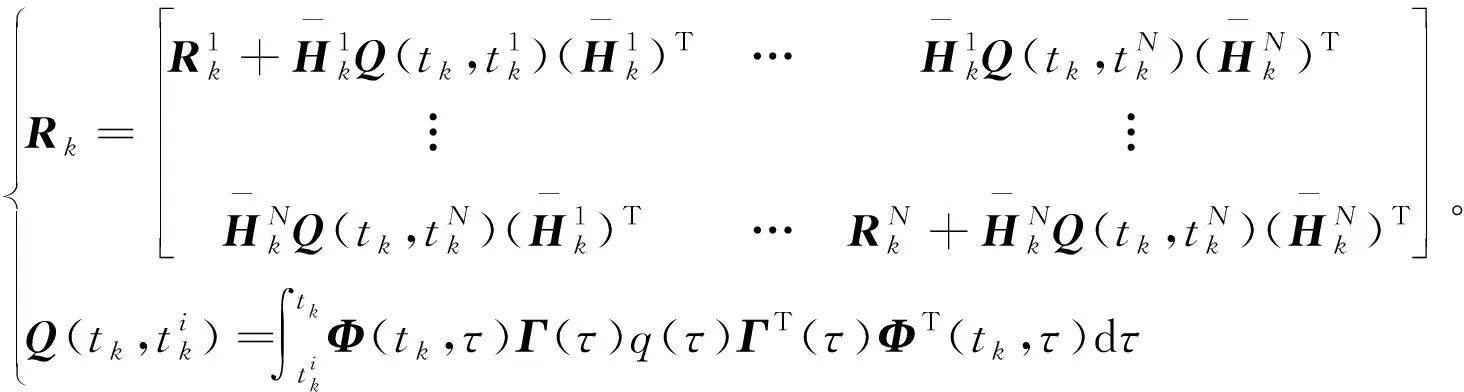
(15)

2 包含無效點濾波的彈道高度預測算法

一組實測彈道高度信息如圖2所示，此實測信息存在量測數據丟包、信息更新速率不足、受到干擾等問題，因此，需要對經典濾波算法進行改進，以降低上述問題帶來的測量誤差，提高測量數據更新速率。

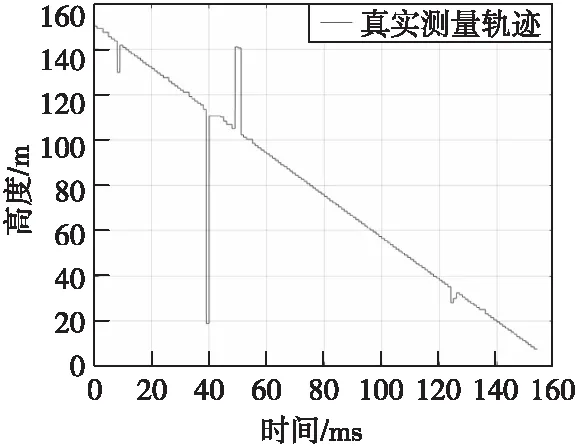
圖2 一組實測彈道高度信息Fig.2 A set of measured ballistic altitude information

2.1 無效點預測流程

本文引入無效點概念，利用偽測量方法，在不進行復雜插值計算的前提下對這些問題一次性完成處理。

當檢測到以下三種場景時引入無效點概念：1)每次檢測到輸入的測量值連續不變或出現漏點時，將連續不變的點或漏點設置為A類無效點；2)檢測到出現超過預設閾值的極端跳變點時，將超過閾值的點設為A類無效點；3)在每兩個采樣點間進行插點，如需將測量數據更新速率提高P倍，可在原離散測量值的每兩個點之間插入P-1個新點，并將這P-1個新點設為B類無效點。之后，利用系統狀態方程、擴展卡爾曼濾波、偽測量算法對無效點進行預測和更新。

對無效點的預測流程如下：

步驟2)對修改后的量測信息進行一次擴展卡爾曼濾波處理。

步驟3)對于B類無效點，為了減少計算量和減少量測誤差的影響，對步驟2)中的每個采樣點的卡爾曼濾波結果，代入預測方程式(3)進行預測，得到連續的P-1個B類無效點中首個點的預測結果，狀態轉移矩陣的參數t取T/P；對其余P-2個B類無效點，每一個無效點的結果由前一個無效點通過式(3)進行預測，誤差協方差陣由式(7)更新。

步驟4)用步驟3)的預測結果作為高度估計結果，由于原始量測信息的每兩個采樣點間插入了P-1個預測點，因此測量數據更新速率提高了P倍，理論上P可以取任意正整數值。

2.2 額外點預測流程

實際應用中，當引信持續受到干擾時有效量測信息持續丟失。因此，需要對高度信息進行額外預測。

由于無效點預測流程具有可以預測無數據點的功能，因此也可實現額外點預測，且理論可以額外預測任意點之后的結果，額外預測的點數越多，與實際值偏差越大。

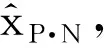
圖3為B類無效點預測流程和用同樣方法進行額外點預測的流程。圖中，P：采樣率提高的倍數(如采樣間隔由20 ms提高到0.5 ms，則P=40)；N：原始信號序列長度；額外預測點數=M·(P-1)。

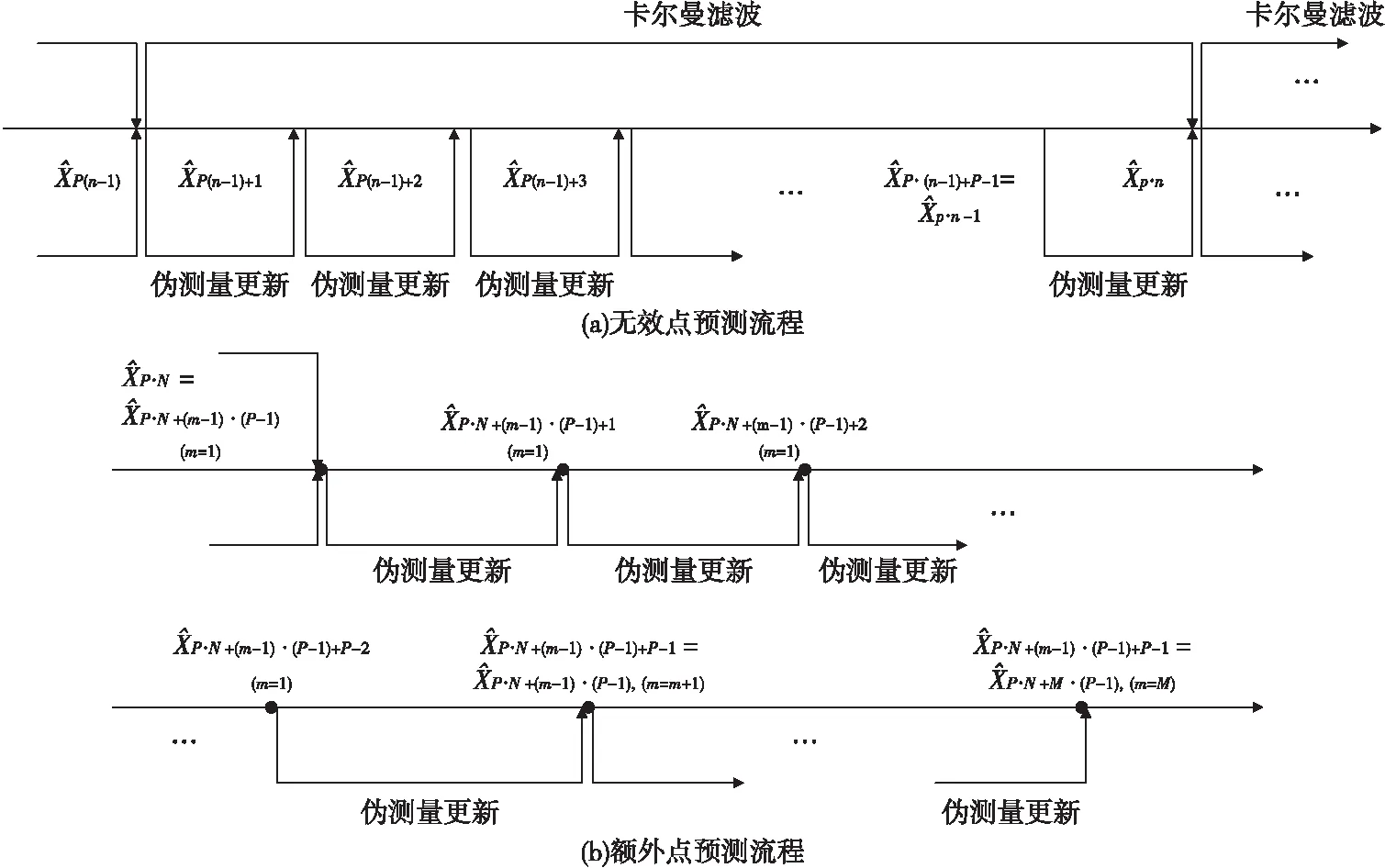
圖3 部分預測流程Fig.3 Partial prediction process

在進行上述預測和更新流程后，可得到高精度、高測量數據更新速率、具有額外預測點數的高度信息，該信息可用于實現引信高精度炸點控制。

3 仿真分析

3.1 模擬數據仿真結果

假設彈道起點高度為160 m，初始速度1 000 m/s，先進行加速度為10 m/s2的勻加速運動，后在第105 ms和第120 ms時因機動原因，分別開始進行變加速和勻速運動，如圖4所示。

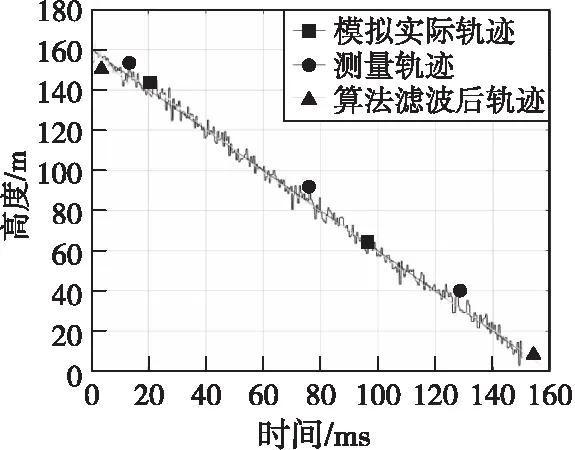
圖4 測量與濾波軌跡Fig.4 Measurement and filter trajectory

仿真驗證算法對高度測量信息量測精度及更新速率的提升效果，擬將更新速率從0.5 ms提高至0.1 ms。設信號測量誤差服從均值為0、方差為9的正態分布，采用本文提出的包含無效點濾波的預測算法，忽略噪聲相關性，選用勻加速運動模型進行濾波計算，在濾波的結果上，額外進行64點預測，即可額外預測約6.4 m的高度數據。蒙特卡洛仿真次數取100次，仿真結果如圖4—圖8所示。

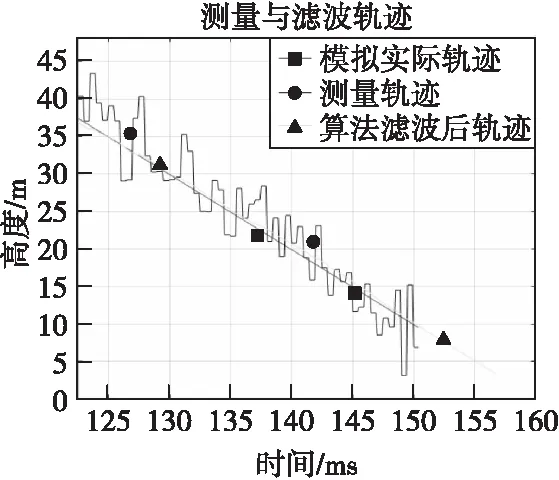
圖5 測量與濾波軌跡局部放大圖Fig.5 Measurement and fusion of the fusion trajectory

圖4、圖5為軌跡和濾波融合處理結果示意圖，圖6—圖8為處理前后位置信息誤差對比圖。

由圖4、圖5可知，本文算法可將采樣間隔從0.5 ms提高到0.1 ms，距離分辨率從0.5 m提高到0.1 m，且額外預測了約6.4 m之后的高度信息。

圖6、圖7、圖8分別為信號處理前后高度、速度和加速度信息誤差對比圖。相比于原始信息，使用本文提出的彈道高度預測算法可以顯著降低測量誤差，融合前后誤差統計如表1所示。

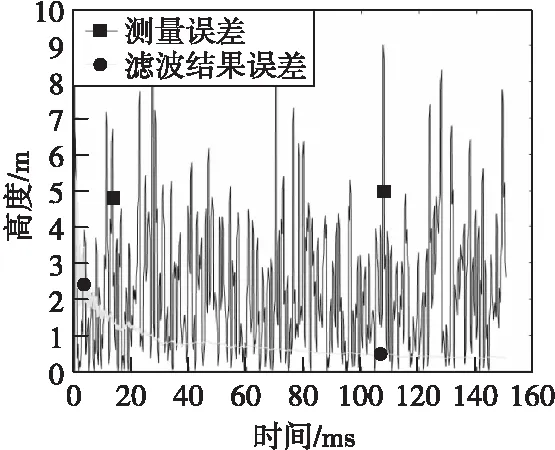
圖6 高度信息絕對誤差Fig.6 Altitude information absolute error

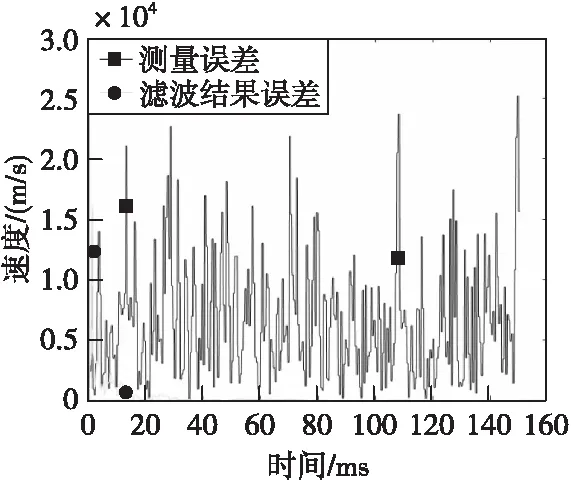
圖7 速度信息絕對誤差Fig.7 Velocity information absolute error

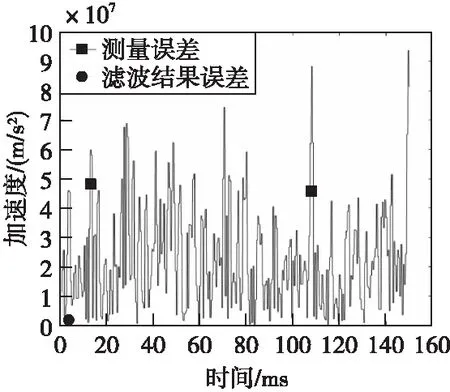
圖8 加速度信息絕對誤差Fig.8 Acceleration information absolute error

表1 濾波前后誤差對比Tab.1 The comparison of the error of filtering

3.2 帶環境噪聲信號仿真結果

仿真模擬信號受到隨機環境噪聲時的濾波效果，噪聲均值為0，仿真得到在不同強度的環境噪聲下算法對檢測誤差的改善效果，結果如表2所示。

由表2數據可知，當量測信息持續受到環境噪聲干擾時，算法仍有較好的收斂效果。

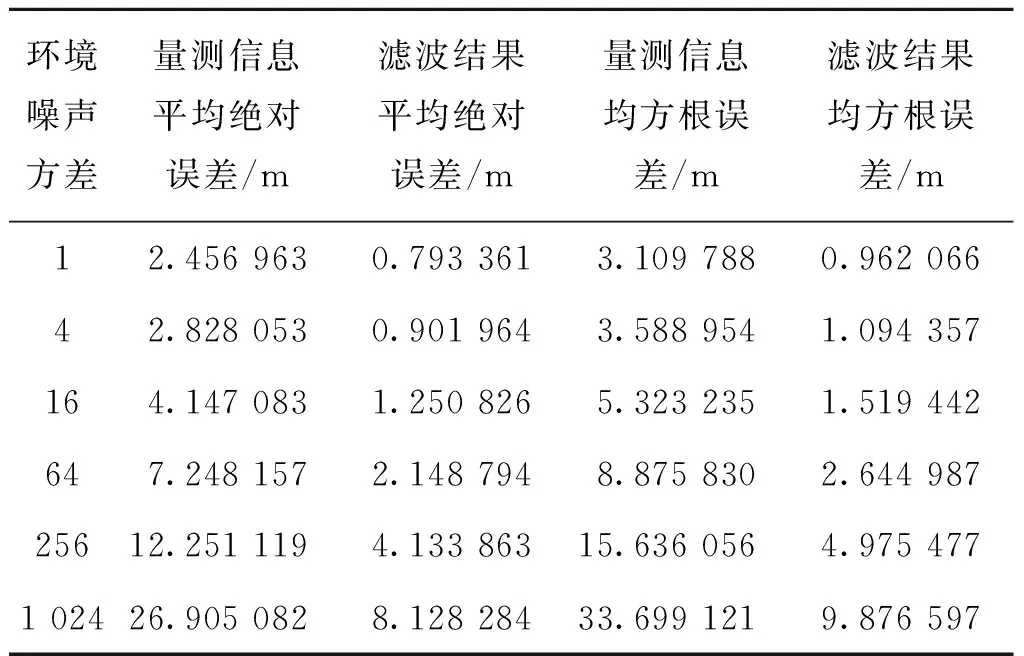
表2 不同環境噪聲下誤差對比Tab.2 Error comparison of different ambient noise

當環境噪聲方差小于4時，濾波結果均方誤差相比無環境噪聲時僅提高不到20%，可以認為此時環境噪聲對算法效果無明顯影響。

當環境方差達到256時，濾波結果均方根誤差約4.98 m，遠大于原始量測信息的均方根誤差約3 m。此時，可認為算法失去有效判斷炸點的能力。

圖9—圖12為環境噪聲方差為64時的濾波結果，仿真驗證了在環境噪聲的影響下算法的有效性。

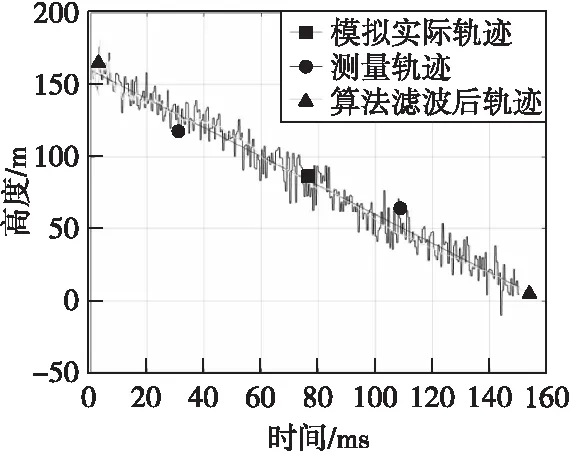
圖9 測量與濾波軌跡Fig.9 Measurement and filter trajectory

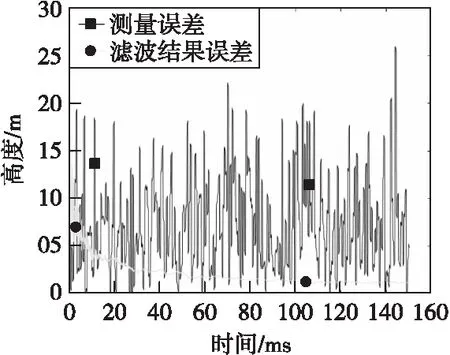
圖10 高度信息絕對誤差Fig.10 Altitude information absolute error

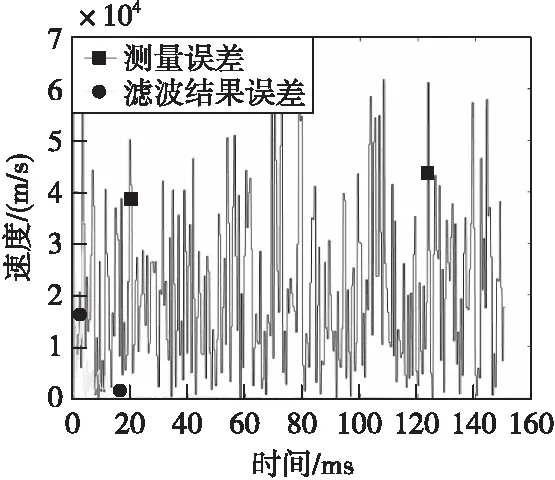
圖11 速度信息絕對誤差Fig.11 Velocity information absolute error

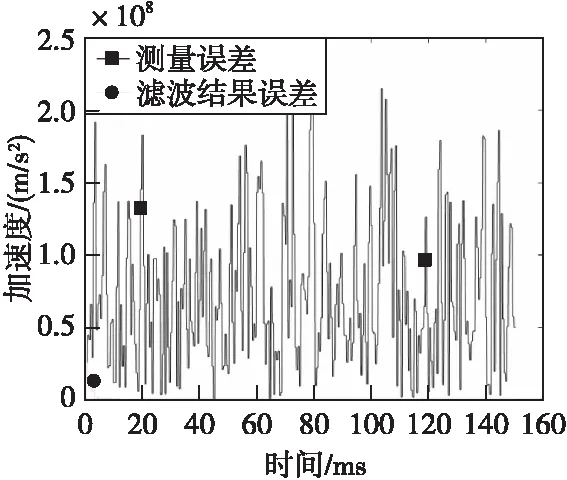
圖12 加速度信息絕對誤差Fig.12 Acceleration information absolute error

3.3 帶干擾點信號仿真結果

仿真模擬測量信息受到點干擾時的濾波效果，設置量測信息受到方差為4的隨機環境噪聲影響，同時受到4處距離干擾，干擾持續時間分別為2，1.5，2，1 ms，干擾平均偏移為45 m，并且信號從第105 ms開始存在持續4 ms的漏點，導致持續上報相同的距離信息，仿真結果如圖13—圖17所示。

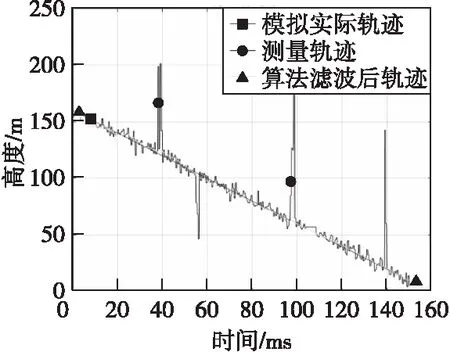
圖13 測量與濾波軌跡Fig.13 Measurement and filter trajectory

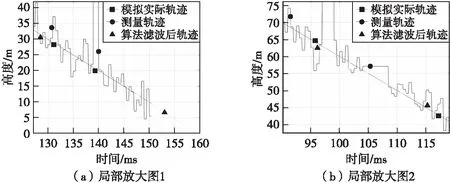
圖14 測量與濾波軌跡局部放大圖Fig.14 Measurement and filter of the fusion trajectory

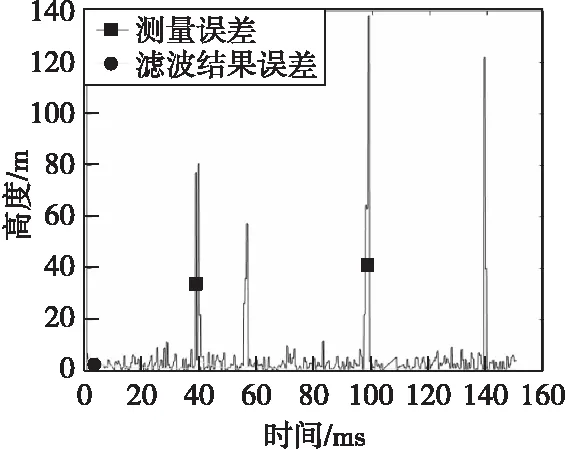
圖15 高度信息絕對誤差Fig.15 Altitude information absolute error

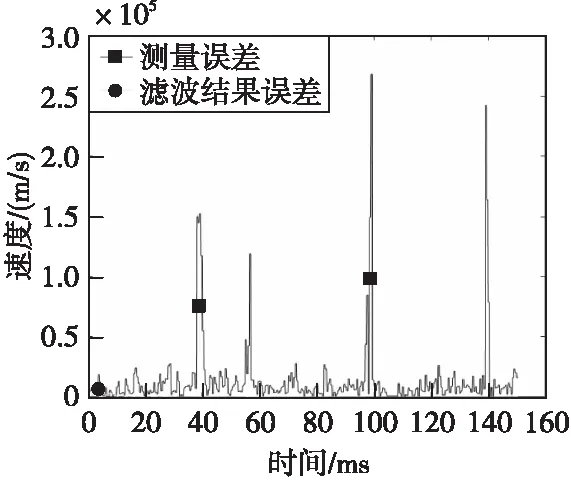
圖16 速度信息絕對誤差Fig.16 Velocity information absolute error

圖17 加速度信息絕對誤差Fig.17 Acceleration information absolute error

圖13、圖14為軌跡和濾波結果示意圖，圖15—圖17為濾波前后高度、速度、加速度信息誤差對比圖。由圖14可見，本文算法能夠在提高測量數據更新速率、提升預測精度、消除漏點的同時，對彈道高度測量中存在的干擾點具有良好的抑制效果。加干擾點和漏點信號的濾波前后誤差統計如表3所示。

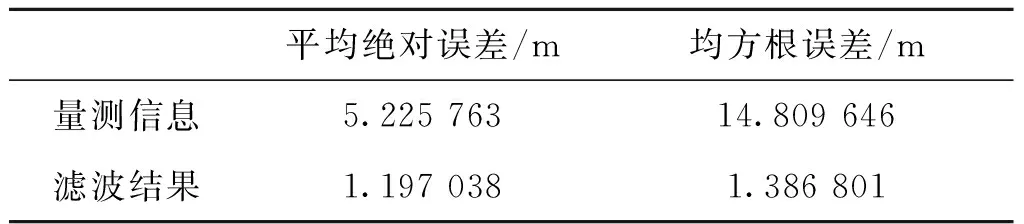
表3 濾波前后誤差對比Tab.3 The comparison of the error of filtering

相比于傳統插值算法，本文算法具有實時性高、抗噪能力強等優點，可有效提升對地近炸引信對地測高精度與抗干擾能力。

4 結論

本文提出一種包含無效點濾波的彈道高度預測算法。該算法通過引入無效點概念，建立流程將探測漏點、受干擾點和需插值點設置不同類型的無效點；為抗持續干擾可以設置任意數目和數據更新速率的額外預測點；分別對無效點和額外預測點利用系統狀態方程、擴展卡爾曼濾波、偽測量技術等算法進行彈道高度信息預測。

仿真驗證結果表明，本文算法在提高數據更新速率、消除漏點干擾、彈道高度額外點預測、降低隨機噪聲干擾等方面效果顯著，經算法處理的彈道高度信息平均絕對誤差和均方根誤差相比原始信號均有明顯降低。相比于傳統插值算法，本文算法具有實時性高、抗噪能力強等優點，可用于無線電引信識別與控制技術領域，能有效改善彈道高度測量中觀測信號可能出現的有效數據缺失、數據更新速率低，因環境噪聲和干擾造成測距精度下降的問題。