基于三點偏置刀位偏差補償?shù)奈遢S側(cè)銑加工路徑優(yōu)化方法＊

陳力智 周立峰 王 東 馬 馳 于建華

（中國航發(fā)商用航空發(fā)動機有限責(zé)任公司，上海 200241）

五軸側(cè)銑加工通過刀具側(cè)刃移除工件表面材料，加工效率高、銑削質(zhì)量好，因而被廣泛用于渦輪和葉輪等非可展直紋面零件的加工[1]。由于非可展直紋曲面的扭曲特性，直母線刀具與曲面完全貼合十分困難，但合理規(guī)劃刀位可以減小刀具與曲面之間的偏差，為達(dá)此目的，研究人員提出了諸多側(cè)銑加工路徑的生成方法。

Liu X W[2]提出了刀具定位的雙點偏置法，Redonnet J等[3]發(fā)展了三點偏置法，嚴(yán)濤等[4]則考慮了刀具與曲面之間四點接觸的情形，并建立了描述模型，但這些方法僅適用于圓柱刀。圓柱刀與圓錐刀是兩種常見的直母線刀具，但后者可以在同樣尺寸下保持更高的剛度，因而避障性更好，更適用于葉輪等復(fù)雜結(jié)構(gòu)零件的加工。圓錐刀的幾何性質(zhì)較圓柱刀更為復(fù)雜，導(dǎo)致適用于圓柱刀的定位方法很難直接用于圓錐刀。常見的圓錐刀定位方法是兩點偏置法，盡管三點偏置法可以帶來更高的定位精度，但現(xiàn)有關(guān)于錐刀三點偏置定位的模型[5]形式復(fù)雜，求解困難，限制了其在加工中的應(yīng)用與集成。值得注意的是，多點偏置得到的刀位往往不能最小化刀具與曲面之間的加工偏差[6]，在使用多點偏置法確定刀位序列后，往往需要對刀軸進(jìn)行進(jìn)一步優(yōu)化。

宮虎等[7]分析了圓柱刀與非可展直紋面幾何偏差的性質(zhì)，給出了偏差極值最小條件下刀軸偏置點的確定方法，并采用最小二乘模型逼近這些散點以確定刀具軸跡面。劉紅軍等[8]在柱形刀三點偏置定位的基礎(chǔ)上，采用密切法進(jìn)一步優(yōu)化刀軸以提高加工精度。針對錐形刀五軸側(cè)銑加工，孔馬斌等[9]通過對圓柱刀施以旋轉(zhuǎn)確定圓錐刀的初始刀位，然后調(diào)整刀軸上的三點減小編程誤差。閻長罡等[10]使用兩點偏置法確定初始刀位序列，在此基礎(chǔ)上提出了基于偏差補償?shù)牡毒咻S跡面擬合方法。然后，他們通過構(gòu)造設(shè)計曲面的相伴曲面，建立了基于響應(yīng)面法的圓錐刀側(cè)銑路徑優(yōu)化模型[11]。因為刀軸與加工誤差存在高度非線性的關(guān)聯(lián)，部分學(xué)者研究了基于智能算法的側(cè)銑刀路優(yōu)化方法。Kuo C L等[12]提出了慮及插補誤差的側(cè)銑刀位優(yōu)化模型，并使用粒子群（PSO）法、類電場（EM）法等智能算法尋求最優(yōu)解。韓軍[13]等使用模擬退火算法和粒子群算法（SA-PSO）的混合算法提升了單一智能算法在側(cè)銑刀路優(yōu)化中的求解效果。

由以上方法可以看出，基于偏差補償策略的刀路優(yōu)化方法仍是提高五軸側(cè)銑加工精度的主流手段，但對于錐形銑刀初始定位，缺乏便捷的三點偏置模型；此外，最小二乘模型被廣泛用于刀具軸跡面對理想偏置點的逼近，該模型的求解只關(guān)注數(shù)學(xué)意義上的偏差最小，并不能真實反映求解所得路徑引起的誤差變化。針對以上問題，首先建立解析的圓錐刀兩點偏置模型，通過引入滑移區(qū)間，搜索得到其三點偏置刀位。在此基礎(chǔ)上，分析刀軸偏置點的理想分布，并據(jù)此建立軸跡面擬合模型，通過奇異值分解（SVD）算法求解該模型，對比不同求解路徑對應(yīng)的加工誤差，選擇最小值得到最優(yōu)加工路徑。

1 直母線刀具的三點偏置方法

圓柱刀與圓錐刀均是直母線刀具，圓柱刀可視作圓錐刀錐角為零的特例，因而適用于圓錐刀的定位方法很容易拓展到圓柱刀，本節(jié)以圓錐刀為研究對象，提出了通用的刀具定位模型。

首先，非可展直紋面R(u,v)的表達(dá)形式如下：

式中：u為沿邊界線方向的參數(shù)，B1(u)是下邊界線，B2(u)是上邊界線；v是沿曲面直母線方向的參數(shù)。錐形刀的底圓半徑為r0，錐角為α，三點偏置條件下刀具與曲面的接觸位置分別位于上、下邊界線，以及曲面中間的u-曲線R(u,0.5)。假設(shè)刀具與曲面在下邊界線的接觸位置為R(u0,0)，根據(jù)錐刀的幾何性質(zhì)，可以計算R(u0,0)對應(yīng)刀軸上的一點為

式中：Q1為 下邊界線對應(yīng)刀軸上的偏置點，n(u0,0)是R(u0,0)處曲面的單位法矢，曲面上任意一點的單位法矢可由下式計算：

其中：Ru和Rv分別是R(u,v)沿u向與v向的一階切矢量。如果刀具與曲面的第二接觸位置位于曲面上邊界線的一點R(u1,1)，則R(u1,1)對 應(yīng)刀軸上的一點應(yīng)滿足如下方程：

其中：r是R(u1,1)與Q2的距離，其與底圓半徑的關(guān)系為

將r視作變量x，聯(lián)立方程（2）、（4）、（5）可得：

其中：

式（6）是一元二次方程，一般存在兩解，選大于r0的 正解作為最終解，代入方程（4）得到Q2，進(jìn)而可以確定當(dāng)前刀具的刀軸I為I=(Q1Q2)/∥Q1Q2∥，刀具底面圓的中心點O為O=Q1?Irtan(α)。

對于確定的兩點偏置刀位，在Q1和Q2限定的區(qū)間內(nèi)對刀軸進(jìn)行均勻采樣，采樣點集為計算Pi向設(shè)計曲面的投影，如圖1所示，所得投影點為Ri，PiRi與刀具靠近曲面一側(cè)的交點為Mi，由此可得與Pi對應(yīng)的曲面偏差為

圖1 刀具與曲面偏差計算示意圖

如果 εi為正，則該偏差表示為欠切；如果εi為負(fù)，則該偏差表示為過切；否則，表明刀具與曲面在Ri接觸。因此，找到R(u,0.5)在刀軸上的法向偏置點并計算其對應(yīng)的偏差 εmid，可以判定二者的接觸狀態(tài)。

如果當(dāng)前刀位下的 εmid不為零，則保持刀具與曲面下邊界線的接觸位置不變，通過更改上邊界線的參數(shù)值重新指定刀具與上邊界線的接觸位置，并計算新刀位下的 εmid，直至搜索到 εmid=0的刀位。其中，改變上邊界線參數(shù)值的過程類似于刀具沿著上邊界線滑動。事實上，當(dāng)錐角為零，即刀具變?yōu)閳A柱刀時，所述三點偏置刀位的搜索過程與文獻(xiàn)[7]中介紹的三點偏置方法類似，因此，可以應(yīng)用二分法加速三點刀位的搜索過程。如果在指定滑移范圍內(nèi)，沒有搜索到 εmid=0 的刀位，則返回 εmid最接近0時的偏置刀位。圖2總結(jié)了錐形刀初始刀位的搜索流程，需要注意的是，上邊界線的搜索范圍[ui,s,ui,e]應(yīng)保證刀具在ui,s和ui,e對應(yīng)兩 點偏置刀位的 εmid異號。

圖2 初始刀位規(guī)劃流程圖

2 基于偏差補償?shù)牡堵穬?yōu)化

2.1 加工偏差的近似計算

根據(jù)規(guī)劃所得刀位序列，可構(gòu)建刀具路徑的描述方程。假設(shè)刀位個數(shù)為m，從規(guī)劃刀位中獲取兩組點列，一組是刀具底面圓心另一組是曲面上邊界線在刀軸上的法向偏置點使用三次B樣條曲線對點列進(jìn)行擬合，其中，樣條曲線控制點的個數(shù)不超過規(guī)劃刀位個數(shù)的一半，節(jié)點矢量可選用均勻節(jié)點矢量。由擬合而來的曲線分別記為Cb(t)和Ct(t)，其表達(dá)式如下

式 中：Nl,3(t)和Ns,3(t)是 3次B樣條基函數(shù)，D1,i和D2,i是控制點，其個數(shù)分別為m1和m2。進(jìn)一步，得到刀路的連續(xù)表達(dá)式，即

軸跡面方程：

式中：參數(shù)a、t分別表示沿刀軸方向和進(jìn)給方向的參數(shù)，可見刀具軸跡面也是直紋面，每一個確定的t值都對應(yīng)一個刀位。

雖然加工偏差被定義為刀具運動包絡(luò)面與設(shè)計曲面之間的距離，但這種方式下定義的加工偏差計算較為復(fù)雜，而刀具與曲面之間的幾何偏差亦可精準(zhǔn)反映二者之間的貼合程度，因此采用刀具靜態(tài)輪廓到曲面的距離近似表示真實的加工偏差。與第一節(jié)所述的單刀位偏差計算類似，首先對軸跡面沿其t向和a向分別均勻離散，離散個數(shù)為n1和n2，其中第i行第j列對應(yīng)的離散點為D(ti,aj)；然后通過D(ti,aj)作垂直于設(shè)計曲面的法線，得到法線與刀具曲(面和) 設(shè)計曲面的交點，兩交點之間的距離表示Dti,aj對應(yīng)的法向偏差 εi,j。

2.2 偏差補償模型

如圖3所示，為減小D(ti,aj)對應(yīng)的法向偏差εi,j，可以將D(ti,aj)沿 -εi,jni,j的方向作移動，其中ni,j表示設(shè)計曲面上指向外側(cè)的單位法矢量。考慮到三點偏置定位下，刀具與曲面的偏差值屬于微小量，因此，只需對刀具施以微小移動便可以補償原始偏差。軸跡面上一點的微小移動可用下式描述：

圖3 加工偏差的補償示意圖

其中：?D1,i與?D2,i是控制點變化量，為未知量。D(ti,aj)微 小移動引起的偏差變化為 ?D(ti,aj)·ni,j，位置更新后的D(ti,aj)對應(yīng)的幾何偏差值為

對軸跡面上的每一個采樣點，均可構(gòu)造形如式（11）的方程，而最優(yōu)的刀具路徑應(yīng)保證所有采樣點在位置更新后得到的偏差值平方和最小，所對應(yīng)的優(yōu)化模型為

其中：n1、n2分別是刀軸面兩個方向采用點的總個數(shù)。

2.3 SVD求解

針對式（12）所述模型，其極值條件對應(yīng)的超定線性方程組為

該方程組包含 3(m1+m2)個 方程，式中：A是系數(shù)矩陣，b是常值列向量，x是未知變量組成的向量。式（13）的構(gòu)造方法在其他文獻(xiàn)中已有諸多討論，這里不再贅述。

式（13）的最小二乘解為 (ATA)?1(ATb)，當(dāng)前該解被廣泛視作最優(yōu)解，但該解僅能從數(shù)學(xué)意義上表征線性系統(tǒng)Ax對常數(shù)向量b的最佳逼近，并不能證明其對應(yīng)的精度提升效果最好。這里采用SVD對矩陣A進(jìn)行分解，并據(jù)此得到不同的控制點調(diào)整量，通過對比這些結(jié)果對應(yīng)的加工誤差，篩選出加工精度最優(yōu)的刀具路徑。

為方便敘述，假定A是n3×m3型矩陣，A的奇異值分解結(jié)果為其中 ?的維度是n3×m3，其主對角線上的非零元素代表奇異值，并由大到小順次排列。U和V分別是酉矩陣。?中奇異值對應(yīng)ATA中特征值的平方根。在多數(shù)情況下，奇異值隨著所處維度的增加而快速衰減，因此可以用最大的k個奇異值和其對應(yīng)的U、V矩陣部分來近似矩陣A，即通過改變k值，可以得到矩陣A不同的近似矩陣，在此基礎(chǔ)上，計算這些矩陣最小二乘解得到的控制點偏移量并用于路徑修正，校驗路徑對應(yīng)的加工偏差，進(jìn)而確定其中的最優(yōu)解。

3 仿真與分析

仿真測試軟件為Matlab 2020b，編程計算機的基本配置為：CPU：i5-1240P，RAM：8 GB。測試的非可展直紋面如圖4所示。曲面來自于文獻(xiàn)[12]中的Surf.5和Surf.6，為避免歧義，本文將這兩張曲面記為曲面A和曲面B。曲面A和曲面B的上下邊界線均為3次貝塞爾曲線，表1列出了邊界線的控制點。因為所提方法的適用對象包括圓柱刀，為更好展示所提方法的優(yōu)越性，采用半徑為2 mm的圓柱刀加工測試曲面，并將加工結(jié)果與文獻(xiàn)[12]的結(jié)果對比。其中，加工精度的表達(dá)方式為曲面上所有采樣點加工偏差絕對值之和。曲面上采樣點的分布與文獻(xiàn)[12]保持一致，即對曲面u、v向分別均勻采樣，采樣個數(shù)為。用于路徑優(yōu)化的初始刀位設(shè)定為50個，軸跡面上下引導(dǎo)線控制點的個數(shù)設(shè)為10。表2列出了優(yōu)化所得路徑和文獻(xiàn)[12]中方法在加工精度與生成路徑所需時間的對比，可見所提方法無論在精度，還是計算速度方面，都顯著優(yōu)于文獻(xiàn)[12]所提的基于智能算法的路徑優(yōu)化方法。

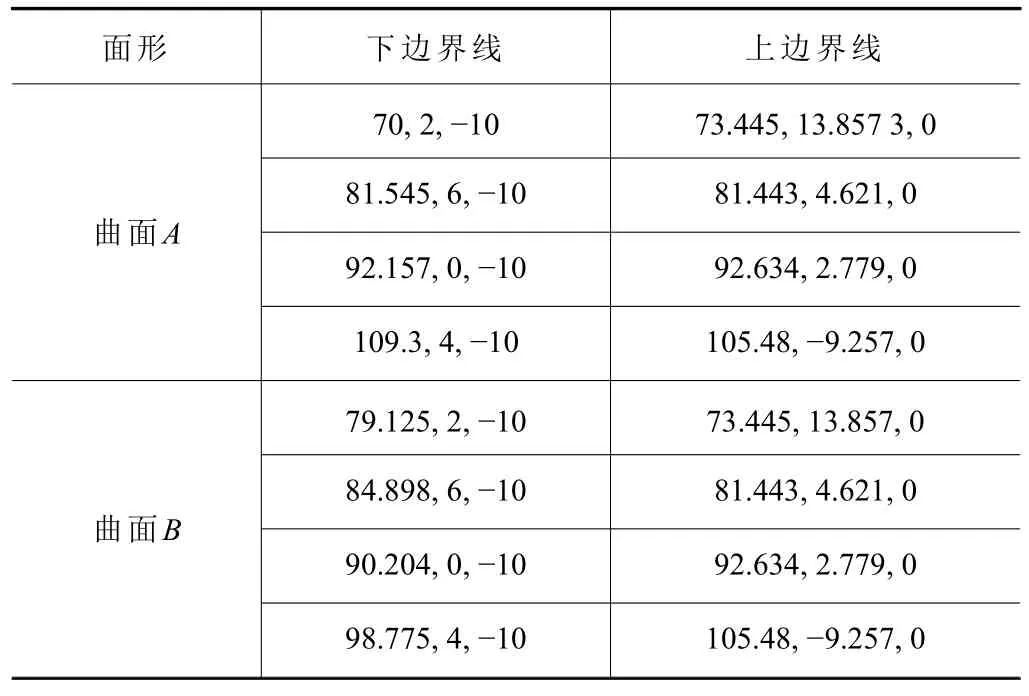
表1 測試曲面上下邊界線的控制點

表2 所提方法與文獻(xiàn)[12]方法的對比

圖4 測試曲面圖

圖5展示了采用不同k值的SVD分解所對應(yīng)路徑的加工精度，可見最優(yōu)的加工精度不一定對應(yīng)原始矩陣A的最小二乘解，而通過對比不同k值下的路徑精度，可以篩選得到加工精度提升效果最大的最優(yōu)路徑。

圖5 曲面A和曲面B的加工路徑在不同k值下的優(yōu)化效果

同樣以曲面A和曲面B為測試對象，當(dāng)選用刀具為錐形刀時，所提方法依舊有效。在此仿真中，測試參數(shù)與圓柱刀的測試保持一致。選用刀具為錐角 α=5，底圓半徑r0=1 mm的錐形刀，圖6展示了使用三點偏置刀位產(chǎn)生的加工偏差分布，其累積偏差值分別為17.832 mm和30.015 mm；圖7展示了在此基礎(chǔ)上優(yōu)化得到最優(yōu)刀具路徑產(chǎn)生的加工偏差分布，優(yōu)化后的累積偏差為9.651 mm和15.802 mm，可見所提方法能夠進(jìn)一步提升非可展直紋面的加工精度。

圖6 初始刀位下曲面 A和曲面 B的偏差分布

圖7 最優(yōu)路徑下曲面 A和曲面 B的偏差分布

4 結(jié)語

（1）提出了錐形刀兩點偏置定位的解析模型，通過二分法滑移尋優(yōu)，得到了錐刀三點偏置刀位。所提方法計算效率高，結(jié)果準(zhǔn)確，生成的三點偏置刀位有助于后續(xù)的路徑優(yōu)化。

（2）建立了基于偏差補償思想的刀軸面優(yōu)化模型，使用SVD篩選得到了加工偏差最小的刀具路徑。在不同測試曲面上與基于智能算法的路徑優(yōu)化方法對比結(jié)果表明，所提方法的加工精度提升為38%和92%，并且所需計算時間也大幅減少。