基于極間虛齒的表貼式永磁電機六倍頻振動噪聲的削弱

李澤星 夏加寬 劉鐵法 郭志研 魯冰娜

基于極間虛齒的表貼式永磁電機六倍頻振動噪聲的削弱

李澤星1夏加寬1劉鐵法2郭志研1魯冰娜1

（1. 沈陽工業大學電氣工程學院 沈陽 110870 2. 中國科學院沈陽自動化研究所 沈陽 110169）

采用極間虛齒結構對表貼式永磁電機的六倍頻振動噪聲進行削弱，與傳統的優化方法相比，該方法結構簡單，且基本不影響基波磁場和平均轉矩。首先，基于麥克斯韋張量法，推導了考慮力波分量相角的六倍頻電磁力諧波表達式，分析了六倍頻電磁力的產生機理，并以一臺8極48槽表貼式永磁電機為例，采用有限元法進行驗證；接著，引入凸極磁導函數，基于磁場調制原理，分析了虛齒對磁通密度時間諧波的調制作用及對六倍頻電磁力的削弱機理；然后，建立多物理場有限元模型，對比了優化前后電機的關鍵電磁性能以及振動和噪聲頻譜，結果表明，極間虛齒可有效削弱電機的六倍頻電磁力和振動噪聲；最后對優化后的樣機進行噪聲實驗，與仿真結果對比，驗證了理論和有限元模型的正確性。

極間虛齒 表貼式永磁同步電機 六倍頻振動噪聲 有限元法

0 引言

永磁電機具有結構簡單、功率密度高、效率高等優點，被廣泛用于水下航行器推進系統[1-3]。然而，隱蔽性作為水下航行器的重要指標，容易受到永磁電機低頻振動噪聲的影響[4-5]。

在低頻段，六倍頻振動噪聲是非常顯著的，其由六倍頻電磁力引起[6-10]。文獻[6-8]分別分析了10極45槽、8極12槽、8極9槽、10極12槽四種分數槽永磁電機的電磁力和電磁振動特性，結果表明，六倍頻振動是主要的峰值點。文獻[9]對一臺8極48槽永磁同步電機進行了噪聲實驗，結果表明，六倍頻電磁力約為二倍頻電磁力的三分之一，但其產生的噪聲幅值卻與二倍頻噪聲基本一致。文獻[10]對一臺8極48槽電動汽車用永磁電機的力波特性進行分析，結果表明，六倍頻電磁力是零階力波的主要頻率分量；通常來講，模態越低，振動越強，較小的低階力波即可引起較大的振動噪聲[11]。六倍頻電磁力與3次、5次和7次磁通密度諧波密切相關，由于這些磁場諧波在永磁電機中占比較大，這導致六倍頻電磁力及其振動噪聲普遍都顯著地存在于各類永磁電機中[12]。因此，針對六倍頻電磁力的分析和削弱是十分必要的。

目前，國內外已有許多學者對電機振動噪聲的削弱方法進行研究[13-18]。文獻[13]以一臺6極36槽永磁電機為例，提出了一種極間填充永磁體的方法來削弱振動，該方法對二倍頻振動噪聲的削弱非常有效，但是對六倍頻振動噪聲的削弱并不明顯。文獻[14]以一臺8極48槽永磁電機為例，基于麥克斯韋張量法，分析了轉子分段斜極對電機徑向力波諧波的影響，結果表明，當轉子被分為5段且斜極角度為3°時，六倍頻電磁力可以被有效降低，但是平均轉矩下降了5%。文獻[15]提出了一種定子齒頂偏移的結構來削弱一臺6極36槽內置式永磁電機的振動，但是平均轉矩下降了4%。此外，還有定子齒削角[16]，斜槽[17]及轉子表面插入銅環[18]等方法，可用來削弱六倍頻振動噪聲，但是這些方法都有一個共性問題，即影響基波磁場，導致平均轉矩嚴重下降。而且，目前基于轉子側的優化方法普遍比較復雜，會導致電機成本的增加和轉子可靠性的降低[9,13,18]。因此，如何在保證平均轉矩基本不變的情況下，提出一種簡單可靠的方法，有效削弱六倍頻振動噪聲是一個亟待解決的問題。

本文采用極間虛齒結構對表貼式永磁電機的六倍頻振動噪聲進行削弱，并基于磁場調制機理[19-20]，解釋了虛齒對六倍頻電磁力諧波及基波磁場的影響。首先，基于麥克斯韋張量法，分析了六倍頻電磁力的產生機理；接著，引入凸極磁導函數，結合有限元模型分析了虛齒對氣隙磁場時間諧波及六倍頻電磁力的影響。然后，建立多物理場耦合模型，對比了優化前后電機的電磁性能及振動噪聲頻譜；最后，將優化后樣機的仿真結果與噪聲實驗結果進行對比，驗證了理論及有限元模型的正確性。考慮到空載狀態的噪聲響應即可反映該電機的噪聲趨勢與特征[21]，因此，為方便起見，本文主要對樣機空載下的六倍頻電磁力諧波進行分析，并使用有限元法驗證了虛齒結構在負載工況的有效性，所得結論可以為表貼式永磁電機六倍頻振動噪聲的削弱提供有價值的參考。

1 電機模型

本文以一臺8極48槽表貼式永磁電機為例進行分析，其橫截面示意圖如圖1所示。電機的基本參數見表1，定子采用斜槽結構，用來削弱槽頻振動[17]。

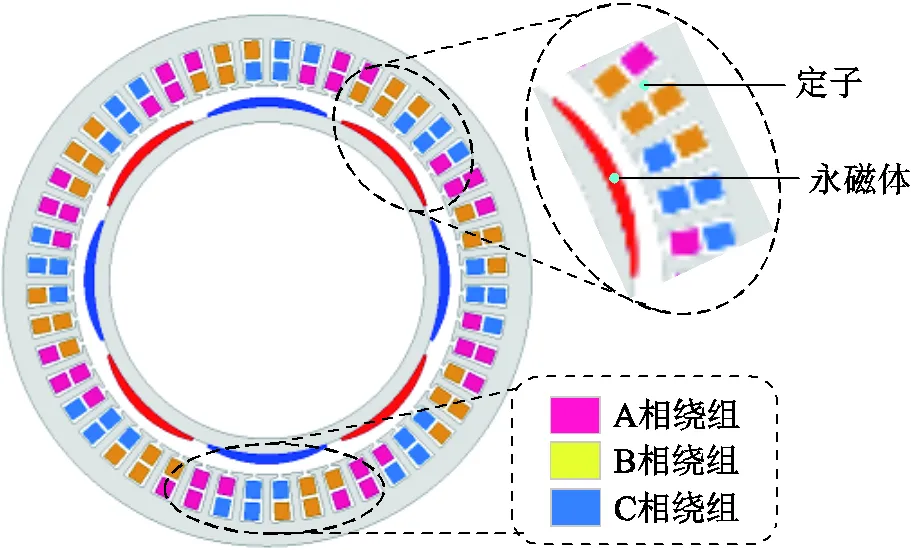
圖1 8極48槽表貼式永磁同步電機橫截面示意圖

表1 樣機基本參數

Tab.1 The basic parameters of prototype

樣機定、轉子簡化示意圖如圖2所示。其中，是轉子位置角，當=0°時，永磁體中心線與定子某個齒的中心線對齊。是轉子相對于參考位置的旋轉角度。

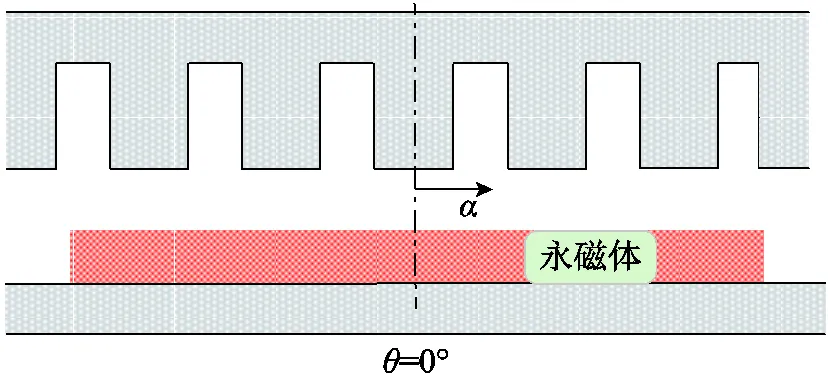
圖2 樣機定、轉子簡化模型

2 六倍頻電磁力諧波產生機理

2.1 六倍頻電磁力諧波解析模型

六倍頻振動噪聲主要由六倍頻電磁力諧波引起，分析六倍頻電磁力諧波的形成原因是降低六倍頻振動噪聲的關鍵。本文基于麥克斯韋張量法與磁場調制機理，分析六倍頻電磁力諧波與磁場諧波的關系，從而得到六倍頻電磁力諧波的產生機理。

定子齒表面相當于等勢面，其中心位置基本不受開槽效應影響，則在永磁磁場作用下，定子齒表面中心線上一點的磁通密度隨時間的變化曲線為[22-24]

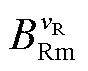
需要強調的是，本文旨在分析六倍頻電磁力時間諧波，其與磁通密度時間諧波直接相關，因此，在磁場分析時，不再考慮磁場的空間分布特性，而主要考慮定子齒表面中心線上一點隨時間（或者隨轉子轉過的電角度）的變化。在分析過程中，基波代表頻率為基頻的諧波，即1次時間諧波。

根據麥克斯韋張量法[25-27]，且忽略幅值較小的切向磁通密度，定子齒表面單位面積上受到的徑向電磁力為[28]

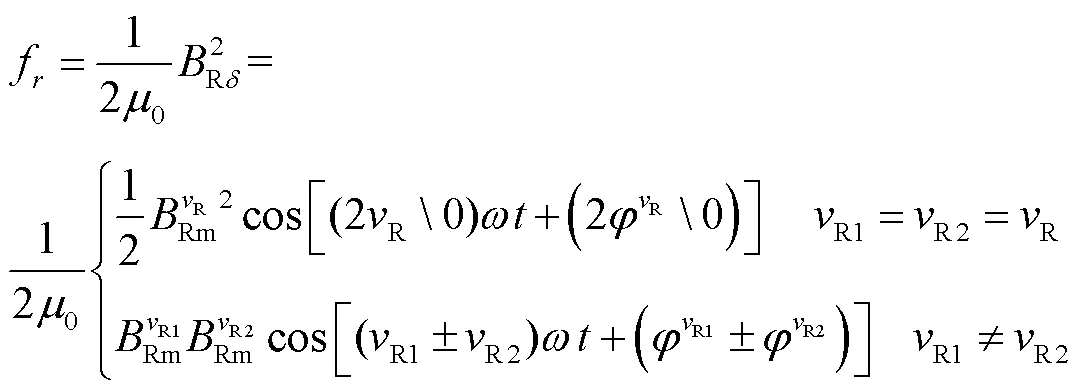
由式（2）可以看出，對于特定的電磁力諧波，其由多個力波分量組成，這些力波分量之間磁通密度諧波含量不同，相互作用關系受到各個分量相位的影響。為方便起見，定義(R1,R2)為由R1和R2次磁通密度時間諧波組成的力波分量。

組成六倍頻電磁力諧波的分量需要

忽略幅值較小的磁通密度高次諧波，主要考慮1、3、5、7次等幅值較大的磁場諧波之間的相互作用，則六倍頻電磁力主要由(1, 5)、(1, 7)、(3, 3)組成，因此，六倍頻電磁力諧波可表示為

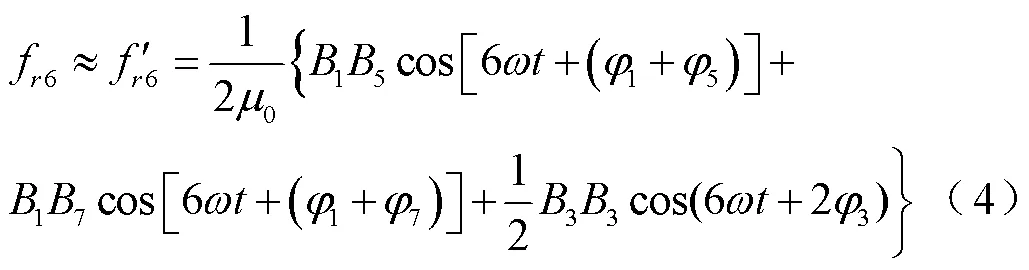
2.2 力波分量之間的耦合關系

結合樣機有限元模型，計算得到磁通密度時間諧波波形及其快速傅里葉變換（Fast Fourier Transform, FFT）分解結果如圖3所示。在圖3b中，通過幅值的正負來區分各次諧波的初始相位；當幅值為正時，相位為0；幅值為負時，相位為π。

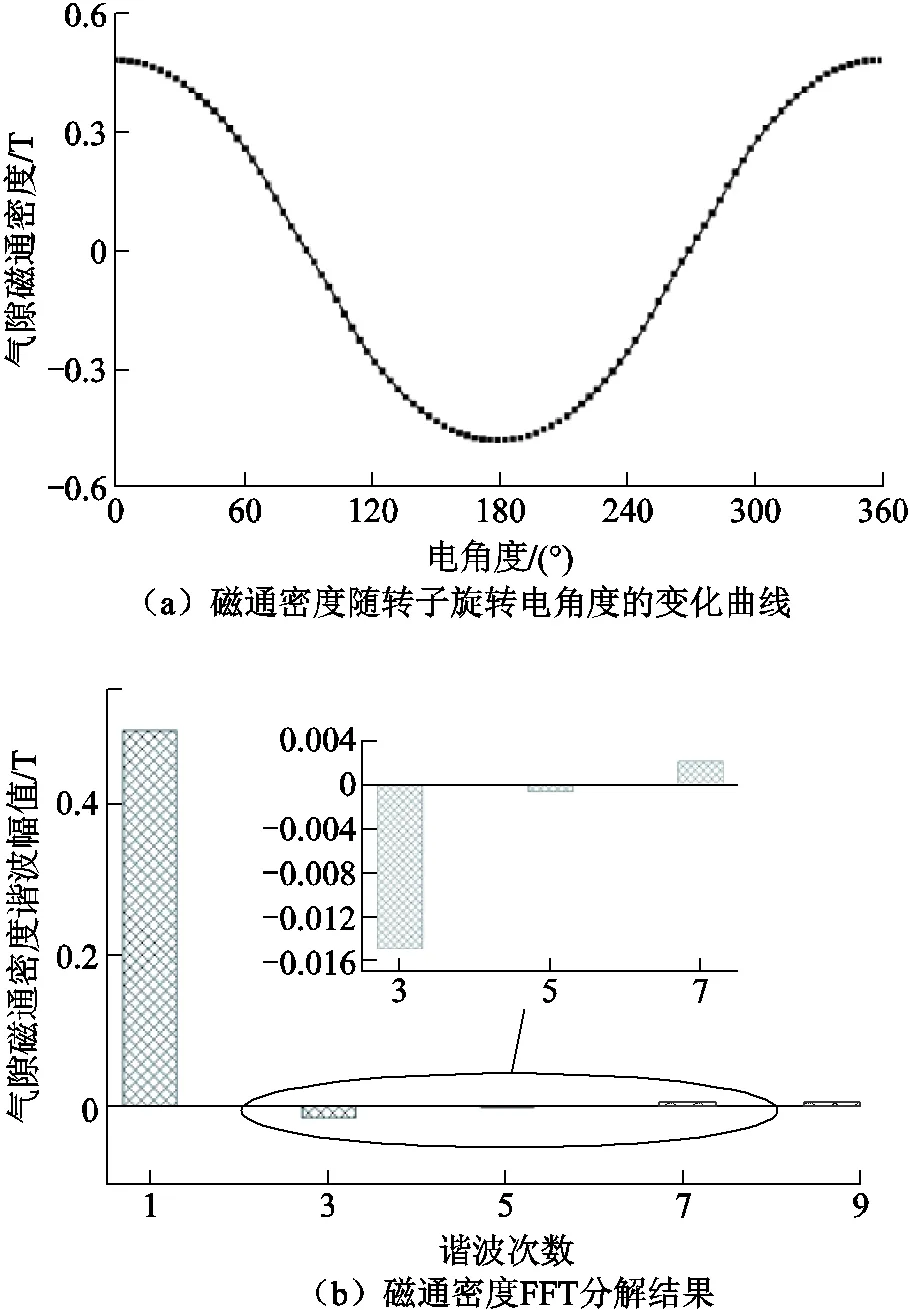
圖3 磁通密度曲線及其FFT分解結果

基于有限元計算結果與式（4），可以確定(1, 7)和(3, 3)為正向分量，(1, 5)為負向分量，即式（4）可簡化為

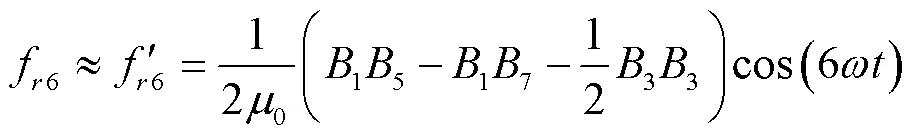
及其各個力波分量的波形及幅值關系如圖4所示，可以發現，由于F(1, 7)和F(3, 3)幅值之和的絕對值大于F(1, 5)幅值的絕對值，導致正負分量之間無法相互抵消，從而引起了六倍頻電磁力。因此，可通過正負力波分量之間的相互補償關系來削弱六倍頻電磁力。從磁通密度時間諧波來看，即盡量減小5次諧波與7次諧波的差值，以及減小3次諧波的幅值。

圖5 與的對比

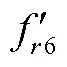
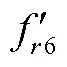
Tab.2 The comparison of amplitudes of and

3 極間虛齒對六倍頻電磁力諧波的削弱

3.1 極間虛齒對磁場時間諧波的影響

加入極間虛齒后轉子橫截面示意圖如圖6所示，兩個相鄰磁極之間增加鐵心凸起結構。該凸起結構類似于定子齒，會導致轉子鐵心具有齒槽效應，但齒間無繞組，因此稱之為極間虛齒。在圓周方向，虛齒與面嵌式永磁電機的極間凸起一致，位于相鄰的永磁體之間，其周向寬度恰好與永磁體互補，可用于永磁體定位。增加虛齒結構的轉子等效簡易模型如圖7所示。在圖7中，為極間虛齒的徑向厚度。本節中，計算結果均以=1.2mm的模型為基礎。

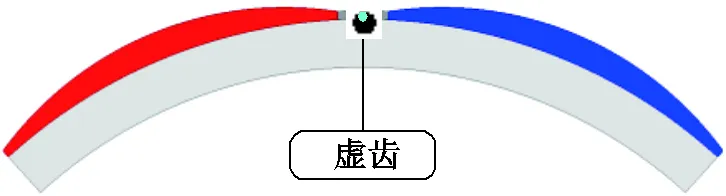
圖6 加入極間虛齒后轉子橫截面示意圖

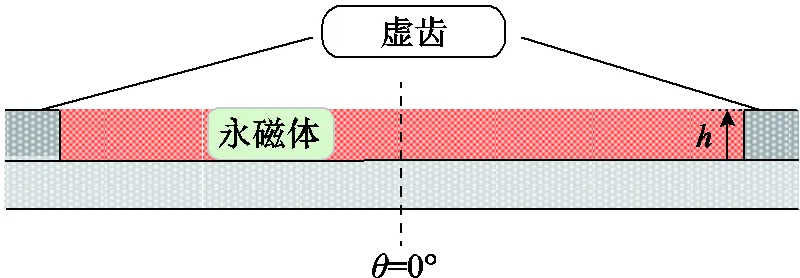
圖7 加入極間虛齒后轉子等效模型

極間虛齒相當于轉子輔助齒，會引起氣隙磁導發生改變。根據已經取得的研究成果[29]，可引入凸極磁導函數來表征虛齒引入的諧波磁導，即

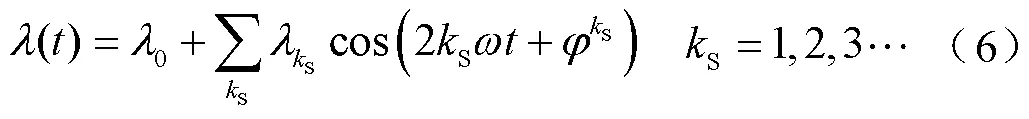
永磁體作用下，定子齒表面中心線一點的磁動勢隨時間變化的表達式為[30-31]

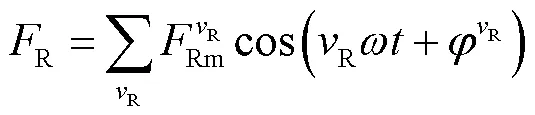
將式（7）永磁磁動勢作用于式（6）凸極磁導函數，可得到該點在虛齒影響下的磁通密度為

對比式（1）與式（8），可以發現，引入虛齒后，磁通密度諧波的頻率成分并沒有變化，但是諧波磁導會對原有磁場諧波形成調制作用，改變與其相差2S次諧波磁通密度的幅值。調制效應與諧波磁導的相位相關，調制程度正比于諧波磁導幅值和相應磁通密度諧波幅值的乘積。

定子齒表面中心上一點的磁導隨時間的變化可表示為

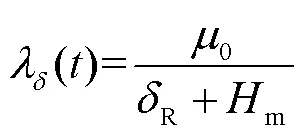
一個電周期內該點磁導隨時間的變化曲線及其FFT結果如圖8所示。圖8中，當幅值為正時，相位為0；幅值為負時，相位為π。

圖8 磁導波形及其FFT分解結果

基于式（8）及有限元計算結果，以3次諧波為例，進一步討論虛齒對磁場諧波的調制效應。由于其他諧波磁通密度幅值較小，僅考慮基波在凸極磁導調制后對3次諧波的影響，且忽略諧波之間相互作用關系的迭代效應。基波磁場可分別與2次磁導與4次磁導相互作用，調制得到3次諧波磁場，由式（8）可以確定，基波與2次磁導相互作用后，得到的3次諧波磁場為負向分量；基波與4次磁導相互作用后得到的3次諧波磁場為正向分量。則調制后，3次諧波幅值變化量為

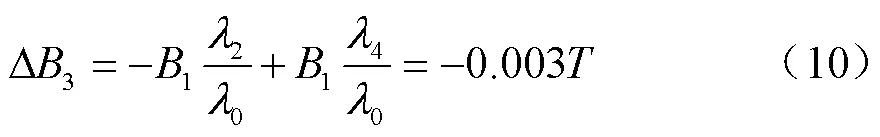
同理，可以得到調制后基波及其他諧波的幅值變化量見表3。表3中，基波的變化量主要由3次諧波與2次和4次磁導分別作用，5次諧波與4次和6次磁導分別作用，7次諧波與6次磁導分別作用得到，由于其變化量較小，結果僅給出了變化量總和。

表3 基波及其他諧波的變化量

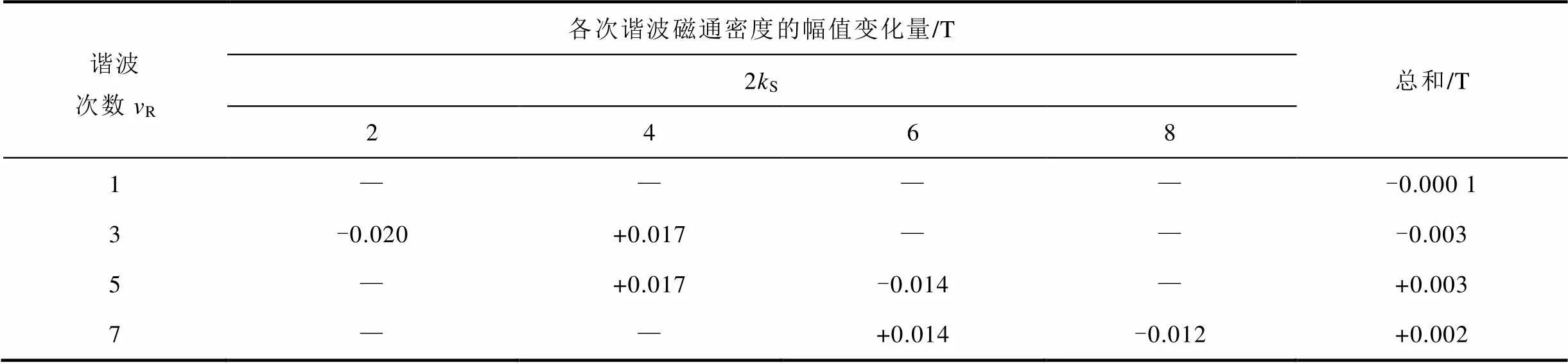
Tab.3 The changes of the fundamental wave and other main harmonics

分析表3可知：

1）由于基波磁場的幅值變化量主要由幅值較小的諧波磁場與相應磁導相互作用得到，變化量較小，基本可以忽略，因此，虛齒基本不影響基波磁場。

2）由于2次諧波磁導幅值大于4次諧波磁導幅值，因此，虛齒對3次諧波磁場表現為削弱作用。

3）虛齒對5次和7次諧波磁場表現為增大作用，而5次諧波磁場增加量大于7次諧波磁場增加量，因此，虛齒的引入減小了5次和7次諧波磁場的差值。

因此，虛齒主要依靠調制作用，降低3次諧波，并減小5次和7次諧波磁場的差值來削弱六倍頻電磁力諧波，且基本不影響基波磁場。

3.2 虛齒對六倍頻電磁力諧波的削弱

加入虛齒后，氣隙磁通密度隨時間的變化曲線及其FFT分解結果如圖9所示。圖9中，為5次諧波和7次諧波差值。各次諧波的變化量與3.1節中計算結果存在差異，但變化趨勢相同。誤差主要由未考慮除基波外其他諧波之間的相互作用以及調制關系的迭代效應引起，并不影響各次諧波的變化趨勢。圖9b中，3次諧波的降低以及5次諧波和7次諧波差值的減小，與3.1節中所得結論基本一致，驗證了3.1節中理論分析的正確性。

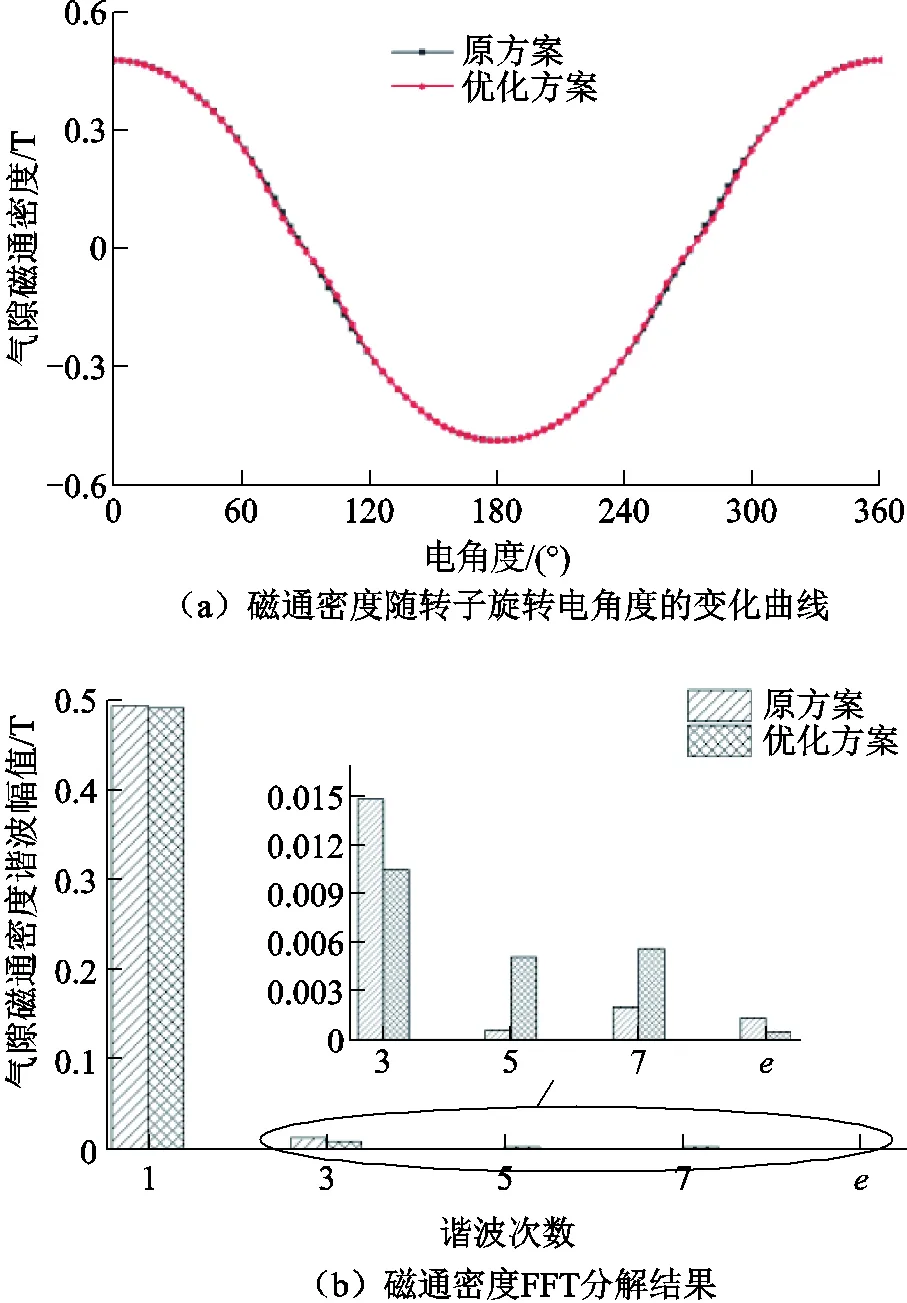
圖9 原方案與優化方案磁通密度對比

虛齒的高度會影響其調制特性，六倍頻電磁力諧波幅值隨虛齒高度的變化趨勢如圖10所示。

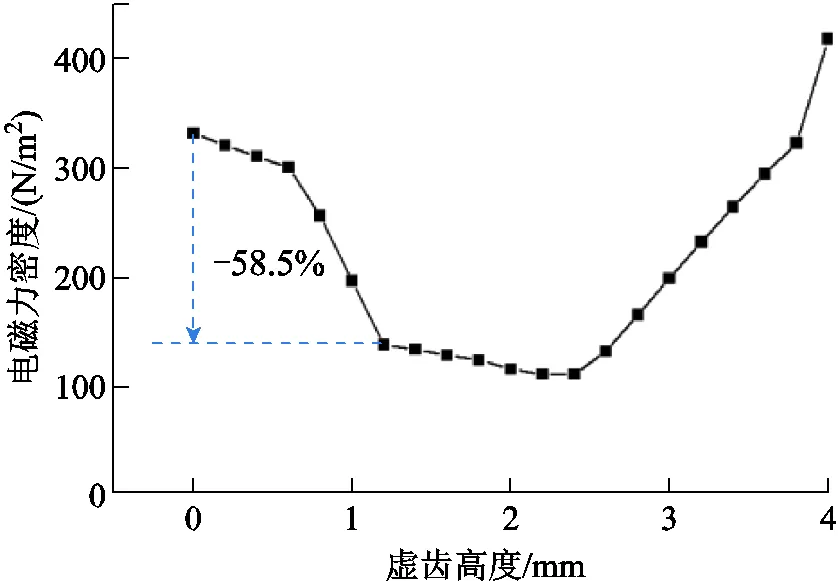
圖10 六倍頻電磁力諧波幅值隨虛齒高度變化曲線

考慮到電機結構，虛齒高度被限定在0～4mm，即不超過永磁體的厚度。可以發現，隨著高度的增加，六倍頻電磁力先減小后增大。

1）在0～0.6mm范圍內，六倍頻電磁力幅值緩慢下降。

2）在0.6～1.2mm范圍內，隨著虛齒高度增加，六倍頻電磁力幅值快速下降。

3）在1.2～2.4mm范圍內，六倍頻電磁力幅值趨于平緩，六倍頻電磁力幅值變化不明顯；=1.2mm恰好為下降速度的轉折點。

4）在2.4～4mm范圍內，六倍頻電磁力幅值逐漸增大。

由于=1.2mm恰好為下降速度的轉折點，繼續增加虛齒高度至2.4mm的過程中，六倍頻電磁力變化并不明顯，因此本文選用=1.2mm作為優化方案，與原方案相比，六倍頻電磁力諧波降低了58.5%。

3.3 優化前后電機電磁性能對比

優化前后空載下電機的電磁力密度隨時間變化曲線及其FFT分解結果如圖11所示。可以看出，除六倍頻電磁力以外，與優化前相比，電機的2倍頻和4倍頻電磁力密度幅值基本不變，8倍頻、10倍頻及12倍頻電磁力諧波略有增大，但是考慮到這三種諧波占比較小，且并非主要的激振源，因此其變化程度基本可以忽略。

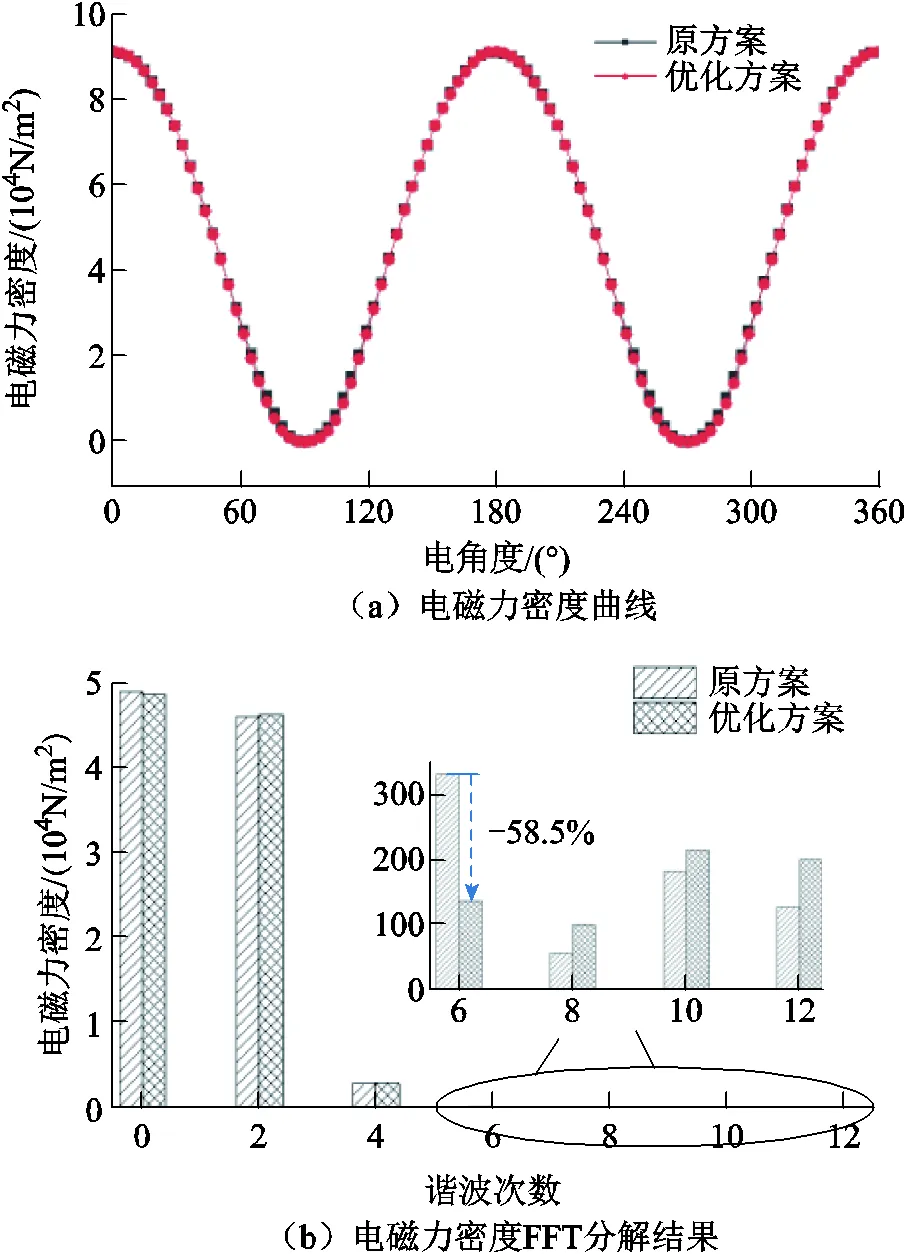
圖11 空載下原方案與優化方案電磁力密度對比

優化前后電機的齒槽轉矩隨時間變化曲線及其FFT分解結果如圖12所示。可以看出，優化后樣機的齒槽轉矩峰峰值有所增大，但是相對于額定轉矩（5.82N·m）來說，其僅占比0.4%，因此基本可以忽略。

圖12 原方案與優化方案齒槽轉矩對比

優化前后負載下電機的電磁力密度隨時間變化曲線及其FFT分解結果如圖13所示。可以看出，六倍頻電磁力諧波幅值明顯下降，因此，極間虛齒結構在空載極負載工況下均可有效削弱六倍頻電磁力諧波。

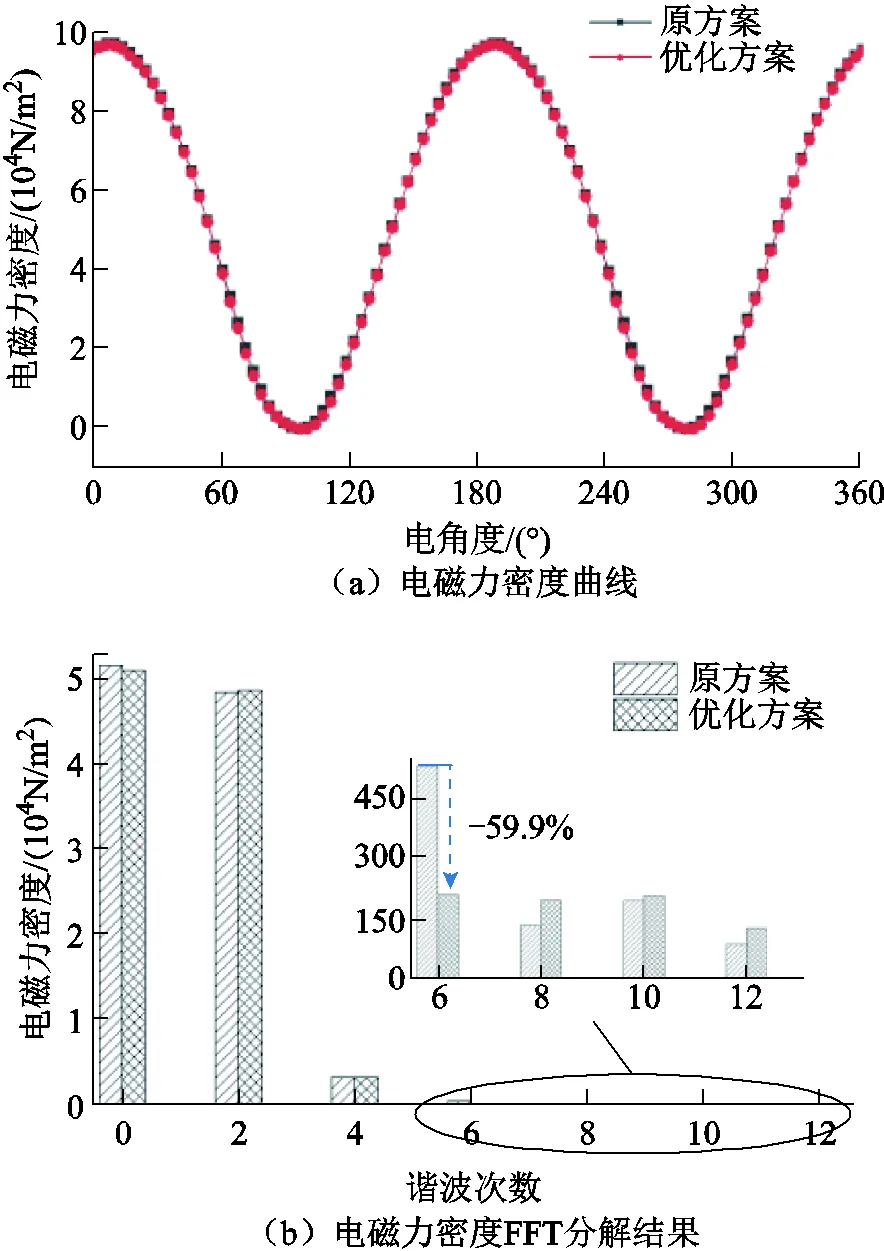
圖13 負載下原方案與優化方案電磁力密度對比

額定電流下，優化前后，電機的平均轉矩曲線如圖14所示，三種情況的平均轉矩見表4。可以看出，當采用d=0方式時，優化后樣機的平均轉矩降低了0.19%，當采用最大轉矩電流比方式時，優化后樣機的平均轉矩降低了0.15%，下降幅度小于d=0控制方式；兩種控制方式下，平均轉矩的下降基本可以忽略。因此，虛齒基本不影響平均轉矩。

圖14 原方案與優化方案平均轉矩對比

表4 原方案與優化方案平均轉矩對比

Tab.4 The comparison of the average torque of the original scheme and the optimized scheme

3.4 虛齒結構對其他極槽配合電機六倍頻電磁力諧波的影響

為了驗證該方法的通用性，本文增加了虛齒結構對不同極槽配合永磁電機六倍頻電磁力諧波的影響分析。8極9槽、8極18槽及10極12槽三種極槽配合永磁電機的有限元模型如圖15所示。

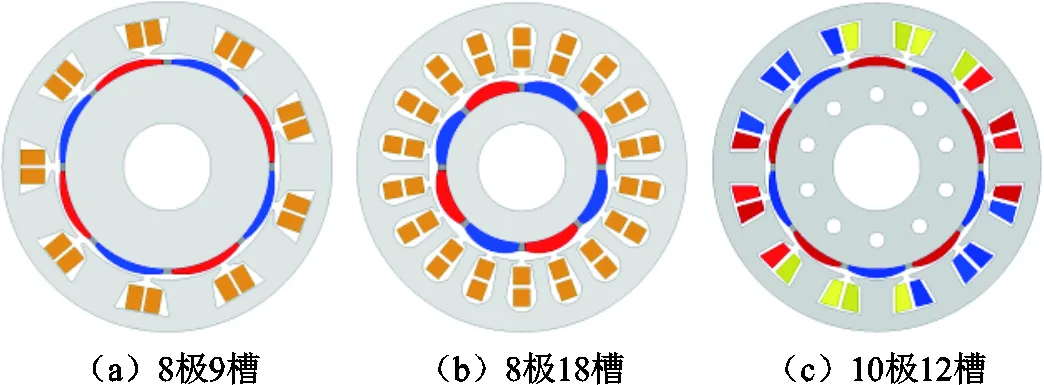
圖15 不同極槽配合永磁電機有限元模型

添加虛齒結構前后，三種極槽配合電機六倍頻電磁力諧波計算結果如圖16所示。可以看出，添加虛齒后，三種極槽配合電機六倍頻電磁力諧波幅值均明顯降低，其中，8極18槽方案六倍頻電磁力諧波下降最明顯，8極9槽方案六倍頻電磁力諧波下降幅度最小。綜合虛齒結構在不同極槽配合電機的應用效果，該方法對六倍頻電磁力諧波的削弱具有較好的通用性。

圖16 不同極槽配合下虛齒對六倍頻電磁力諧波的影響

4 電機振動噪聲分析

4.1 模態分析

樣機定子結構及其3D有限元模型如圖17所示，主要包含定子、機殼、端蓋。

圖17 樣機定子模型

當電機特定階次電磁力頻率接近定子相應模態固有模態頻率時，電機會發生共振現象[10]。優化結構位于轉子，不影響定子結構件模態。定子各階模態振型及其固有頻率如圖18所示。為清晰起見，在展示定子模態振型時，隱藏其他結構件。由圖18可知，額定工況下，計算得到的電機固有頻率與電磁力頻率相差較遠，因此，電機不會發生共振。

4.2 振動響應分析

優化前后樣機的振動頻譜如圖19所示。可以看出，主要的頻率點包括6、12、18等6及其倍數點，其中6處振動加速度幅值最大。與原方案相比，6處振動加速度幅值由0.856m/s2下降至0.475 m/s2，降低44.5%。12處振動加速度幅值略微增加，但與6處幅值相比，仍然較小，因此其變化基本可以忽略。

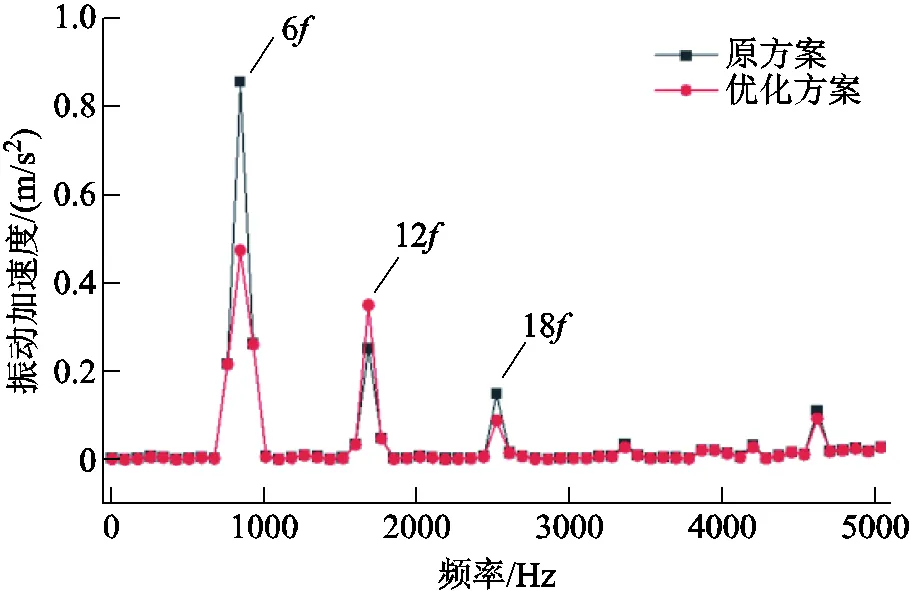
圖19 樣機振動加速度頻譜對比

4.3 噪聲響應分析

優化前后樣機的聲壓級（Sound Pressure Level, SPL）如圖20所示。與振動加速度頻譜相比，趨勢基本一致，主要頻率點仍為6及其倍數點。與原方案相比，6處噪聲幅值明顯下降，證明了本文優化方法的有效性。

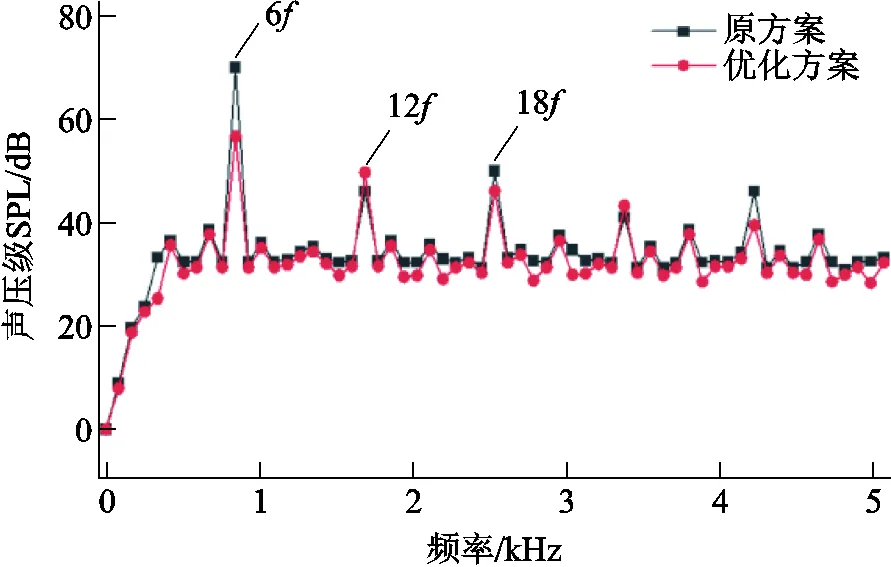
圖20 樣機SPL頻譜對比

5 噪聲實驗

為了驗證分析理論及方法的正確性，本文對優化后樣機進行噪聲實驗。噪聲實驗設置如圖21所示。電機被放在消聲室內，傳感器置于離電機機殼表面1m位置。麥克風及數據采集器均為丹麥BK公司生產。

額定轉速下，噪聲實驗結果如圖22所示。可以看出，仿真結果存在一定誤差，這主要是因為進行有限元仿真時，對模型進行了適當的簡化和等效，且未考慮機械結構及固定方式等因素的影響。但誤差在可接受的范圍內，兩者趨勢基本一致，主要峰值頻率點均為6、12、18等6及其倍數點。因此，有限元結果與實驗結果的對比，可驗證理論分析及仿真結果的有效性。

圖22 SPL頻譜仿真與實測對比

6 結論

本文采用極間虛齒的結構對表貼式永磁電機六倍頻振動噪聲進行削弱。首先，基于麥克斯韋張量法與磁場調制原理，解釋了虛齒削弱六倍頻電磁力的機理；接著，分析了極間虛齒結構在不同工況及電機拓撲結構的有效性；最后，對優化后樣機進行了噪聲實驗, 驗證了仿真及理論的正確性。所得結論可以為表貼式永磁電機六倍頻振動噪聲的削弱提供有價值的參考。

1）六倍頻電磁力主要由(1, 5)，(1, 7)，(3, 3)相互作用得到，其中正向分量與負向分量的差值決定了六倍頻電磁力的大小。

2）虛齒會引起凸極效應，對原有氣隙磁場形成調制作用。以本文8極48槽樣機為例，適當高度的虛齒可以降低3次諧波的幅值，減小5次與7次諧波之間的差值，從而有效地削弱六倍頻電磁力及其引起的振動噪聲。此外，虛齒基本不影響基波磁場及平均轉矩，可以有效保證電機轉矩密度不變。

[1] Liu Guangwei, Qiu Guohua, Shi Jin, et al. Study on counter-rotating dual-rotor permanent magnet motor for underwater vehicle propulsion[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.

[2] Chasiotis I D, Karnavas Y L. A generic multi-criteria design approach toward high power density and fault-tolerant low-speed PMSM for pod applications[J]. IEEE Transactions on Transportation Electrification, 2019, 5(2): 356-370.

[3] Li Wei, Cheng Ming. Investigation of influence of winding structure on reliability of permanent magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 87-95.

[4] Chai Feng, Li Yi, Pei Yulong, et al. Analysis of radial vibration caused by magnetic force and torque pulsation in interior permanent magnet synchronous motors considering air-gap deformations[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6703-6714.

[5] Xu Jiaqun, Zhang Hongqiang. Random asymmetric carrier PWM method for PMSM vibration reduction[J]. IEEE Access, 2020, 8: 109411-109420.

[6] 陳益廣, 韓柏然, 沈勇環, 等. 永磁同步推進電機電磁振動分析[J]. 電工技術學報, 2017, 32(23): 16-22. Chen Yiguang, Han Boran, Shen Yonghuan, et al. Electromagnetic vibration analysis of permanent magnet synchronous propulsion motor[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 16-22.

[7] Sun Tao, Kim Y H, Cho W J, et al. Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[C]//Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 2010: 1.

[8] Zou Jibin, Lan Hua, Xu Yongxiang, et al. Analysis of global and local force harmonics and their effects on vibration in permanent magnet synchronous machines[J]. IEEE Transactions on Energy Conversion, 2017, 32(4): 1523-1532.

[9] 王曉遠, 賀曉鈺, 高鵬. 電動汽車用V型磁鋼轉子永磁電機的電磁振動噪聲削弱方法研究[J]. 中國電機工程學報, 2019, 39(16): 4919-4926, 4994. Wang Xiaoyuan, He Xiaoyu, Gao Peng. Research on electromagnetic vibration and noise reduction method of V type magnet rotor permanent magnet motor electric vehicles[J]. Proceedings of the CSEE, 2019, 39(16): 4919-4926, 4994.

[10] 李曉華, 劉成健, 梅柏杉, 等. 電動汽車IPMSM寬范圍調速振動噪聲源分析[J]. 中國電機工程學報, 2018, 38(17): 5219-5227, 5319. Li Xiaohua, Liu Chengjian, Mei Boshan, et al. Vibration and noise sources analysis of IPMSM for electric vehicles in a wide-speed range[J]. Proceedings of the CSEE, 2018, 38(17): 5219-5227, 5319.

[11] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Analysis of zeroth-mode slot frequency vibration of integer slot permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2954-2964.

[12] 邢澤智, 王秀和, 趙文良, 等. 表貼式永磁同步電機電磁激振力波計算與定子振動特性分析[J]. 中國電機工程學報, 2021, 41(14): 5004-5013. Xing Zezhi, Wang Xiuhe, Zhao Wenliang, et al. Calculation of electromagnetic force waves and analysis of stator vibration characteristics of surface mount permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2021, 41(14): 5004-5013.

[13] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Filling force valley with interpoles for pole-frequency vibration reduction in surface-mounted PM synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6709-6720.

[14] Wang Xiaoyuan, Sun Xibin, Gao Peng. Study on the effects of rotor‐step skewing on the vibration and noise of a PMSM for electric vehicles[J]. IET Electric Power Applications, 2020, 14(1): 131-138.

[15] 謝穎, 李飛, 黎志偉, 等. 內置永磁同步電機減振設計與研究[J]. 中國電機工程學報, 2017, 37(18): 5437-5445, 5543. Xie Ying, Li Fei, Li Zhiwei, et al. Optimized design and research of vibration reduction with an interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(18): 5437-5445, 5543.

[16] 李巖, 李雙鵬, 周吉威, 等. 基于定子齒削角的近極槽永磁同步電機振動噪聲削弱方法[J]. 電工技術學報, 2015, 30(6): 45-52. Li Yan, Li Shuangpeng, Zhou Jiwei, et al. Weakening approach of the vibration and noise based on the stator tooth chamfering in PMSM with similar number of poles and slots[J]. Transactions of China Electrote-chnical Society, 2015, 30(6): 45-52.

[17] Cassat A, Espanet C, Coleman R, et al. A practical solution to mitigate vibrations in industrial PM motors having concentric windings[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1526-1538.

[18] Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. An effective method with copper ring for vibration reduction in permanent magnet brush DC motors[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.

[19] 石玉君, 程子活, 蹇林旎. 兩種典型的場調制型永磁電機的對比分析[J]. 電工技術學報, 2021, 36(1): 120-130. Shi Yujun, Cheng Zihuo, Jian Linni. Comparative analysis of two typical field modulated permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 120-130.

[20] 劉家琦, 白金剛, 鄭萍, 等. 基于磁場調制原理的齒槽轉矩研究[J]. 電工技術學報, 2020, 35(5): 931-941. Liu Jiaqi, Bai Jingang, Zheng Ping, et al. Investigation of cogging torque based on magnetic field modulation principle[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 931-941.

[21] Chiba A. Acoustic noise reduction of switched reluctance motor with reduced RMS current and enhanced efficiency[C]//2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, USA, 2016: 1.

[22] Xing Zezhi, Zhao Wenliang, Wang Xiuhe, et al. Reduction of radial electromagnetic force waves based on PM segmentation in SPMSMs[J]. IEEE Transactions on Magnetics, 2020, 56(2): 1-7.

[23] 于占洋, 李巖, 井永騰, 等. 基于混合磁場解析法的磁極偏心型表貼式永磁同步電機空載特性分析[J]. 電工技術學報, 2020, 35(18): 3811-3820. Yu Zhanyang, Li Yan, Jing Yongteng, et al. No-load characteristic analysis of surface-mounted permanent magnet synchronous motor with non-concentric pole based on hybrid magnetic field analysis method[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3811-3820.

[24] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Effect comparison of zigzag skew PM pole and straight skew slot for vibration mitigation of PM brush DC motors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4752-4761.

[25] Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. Piecewise stagger poles with continuous skew edge for vibration reduction in surface-mounted PM synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8498-8506.

[26] 肖陽, 宋金元, 屈仁浩, 等. 變頻諧波對電機振動噪聲特性的影響規律[J]. 電工技術學報, 2021, 36(12): 2607-2615. Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2607-2615.

[27] 夏加寬, 康樂, 詹宇聲, 等. 表貼式三相永磁同步電機極槽徑向力波補償模型及參數辨識[J]. 電工技術學報, 2021, 36(8): 1596-1606. Xia Jiakuan, Kang Le, Zhan Yusheng, et al. The model of pole slot radial force wave compensation for surface-mounted three-phase permanent magnet synchronous motor and parameter identification[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1596-1606.

[28] 羅玉濤, 盧若皓. 基于結構參數分級優化的電機電磁噪聲抑制[J]. 電工技術學報, 2021, 36(14): 2957-2970. Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2957-2970.

[29] Xia Jiakuan, Li Zexing, Zhang Zixuan, et al. Influence of salient effect on air-gap flux density distribution of interior permanent-magnet synchronous machines[J]. IEEE Access, 2021, 9: 58852-58860.

[30] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Analysis and reduction of electromagnetic vibration of PM brush DC motors[J]. IEEE Transactions on Industry Applications, 2019, 55(5): 4605-4612.

[31] 李曉華, 趙容健, 田曉彤, 等. 逆變器供電對電動汽車內置式永磁同步電機振動噪聲特性影響研究[J]. 電工技術學報, 2020, 35(21): 4455-4464. Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.

Reduction of Six Times Frequency Vibration and Noise of Surface-Mounted Permanent Magnet Synchronous Machines with Interpolar Virtual Teeth

Li Zexing1Xia Jiakuan1Liu Tiefa2Guo Zhiyan1Lu Bingna1

（1. School of Electrical Engineering Shenyang University of Technology Shenyang 110870 China 2. Shenyang Institute of Automation Chinese Academy of Science Shenyang 110169 China）

The permanent magnet synchronous machines (PMSMs) are the most attractive candidates for the use as the power sources for underwater vehicles due to its inherent high efficiency and high power density. However, as an essential performance for the underwater vehicles, concealment is vulnerable to low-frequency vibration and noise caused by PMSMs.

In the low frequency domain, the six-times frequency vibration plays a significant role for PMSMs, which is caused by the six-times frequency force harmonic. The six-times frequency force harmonic is closely related to the fundamental wave, the third-, fifth- and seventh-order magnetic field harmonics. As these magnetic field harmonics account for a large proportion in all magnetic field harmonics, the six-times frequency vibration and noise are generally and significantly present in PMSMs with different combines of pole and slot number. Therefore, it is necessary to analyze and weaken the six-times frequency force harmonic. In this paper, a weakening method of the interpolar virtual teeth is proposed.

After adding virtual teeth, the air-gap flux density and its FFT result are calculated. Compared with the original motor, the 3rdharmonic and the difference between the 5th and 7th harmonics is reduced under the influence of the virtual teeth.

After adding virtual teeth, the electromagnetic force density and its FFT result are calculated. Compared with the original motor, the 2nd and 4th force harmonics are basically unchanged, while the 6th harmonic is significantly reduced by 58.5%.

After adding virtual teeth, the torque on load is calculated. The control mode of the original motor isd=0, and the control modes of the optimized motor with virtual teeth ared=0 and the maximum ratio of torque to current, respectively. Compared with the original motor, the average torque of the optimized motor with virtual teeth is basically unchanged. Therefore, the virtual tooth structure can effectively reduce the sixth harmonic of electromagnetic force while ensuring the torque density.

After adding virtual teeth, the vibration spectrum is calculated. The main frequency points include 6, 12, 18, and the amplitudes of the vibration acceleration at 6is largest. Compared with the original motor, the acceleration amplitude of the optimized motor with virtual teeth at 6decreases from 0.856 m/s2to 0.475 m/s2.

After adding virtual teeth, the noise spectrum is calculated. The trend of noise spectrum is basically the same as the vibration spectrum. Compared with the original motor, the noise amplitude at 6is significantly reduced, which proves the effectiveness of the proposed optimized method.

The noise experiment is carried out in the noise laboratory. The measured results are similar to that of the simulation, and the characteristic points at 6, 12and 18are consistent. Since this simulated project only evaluated the electromagnetic noise, the measured noise may contain other noise sources such as rotor eccentricity, bearing noise and friction noise, which inevitably lead to the difference between calculated values and measured values. However, the simulation results generally meet the required accuracy, and the error is deemed acceptable. Therefore, the theoretical analysis and simulation results are confirmed.

Interpolar virtual teeth, surface-mounted permanent magnet synchronous machines, six times frequency vibration and noise, finite element method

國家自然科學基金資助項目（52077142）。

2021-09-07

10.19595/j.cnki.1000-6753.tces.211436

TM351

李澤星 男，1992年生，博士研究生，研究方向為永磁電機振動噪聲分析及抑制。E-mail：lzxsut@qq.com（通信作者）

夏加寬 男，1962年生，教授，博士生導師，研究方向為永磁電機設計及其控制。E-mail：sygdxjk@163.com

2021-10-18

（編輯 赫蕾）