X射線脈沖星導航的最優觀測周期確定

蘇劍宇，方海燕，，高敬敬，趙良

1．西安電子科技大學 空間科學與技術學院，西安 710126 2．北京臨近空間飛行器系統工程研究所 空間物理重點實驗室，北京 100101

X射線脈沖星導航（X-ray Pulsar-based Navigation，XPNAV）是一種新型的自主導航技術，可為航天器提供位置、時間等導航信息［1-4］，實現航天器高精度自主導航。目前，國內外相繼開展了X射線脈沖星導航試驗，如中國空間實驗室天宮二號（Tiangong-2， TG-2）的γ暴偏振探測科學實驗［5］，中國首顆X射線脈沖星導航試驗衛星（XPNAV-1）在軌開展的X射線脈沖星的探測與脈沖星導航體制的驗證［6-7］，以及國內首顆空間X射線天文硬X射線調制望遠鏡衛星（Hard X-ray Modulation Telescope，HXMT） Insight-HXMT的脈沖星定軌精度驗證實驗［8］。如美國NICER（Neutron star Interior Composition Ex?plorer）項 目 的SEXTANT （Station Explorer X-ray Timing And Navigation Technology）搭載國際空間站（International Space Station， ISS）開展的定軌精度驗證工作［9］。可見，X射線脈沖星觀測與導航驗證工作正進入蓬勃發展的時期。XPNAV的基本原理可描述為［10］：在脈沖星觀測周期內，航天器上安裝的X射線探測器會記錄到一串光子到達時間（Time of Arrivals，TOA），利用觀測的光子TOA，通過一定的算法提取出在這段觀測時間內的某一時刻處航天器所接收的脈沖星信號的相位以及多普勒頻率，由于航天器在任意時刻觀測的脈沖信號相位和頻率都可以用該時刻的位置、速度以及太陽系質心（Solar System Barycenter， SSB）處的脈沖星信號模型準確表示，因此以估計得到的航天器在某一時刻的觀測信號相位和多普勒頻率作為導航觀測量，并將其表示為有關航天器在該時刻位置和速度的關系式作為導航觀測方程，獲得任意時刻的觀測相位即可得到相應時刻的位置信息。高精度的觀測脈沖相位估計是整個導航的難點，為此，國內外學者也相繼提出許多脈沖相位估計算法［11-18］。

在上述導航算法中，為獲得高精度的位置與速度估計，需要實現觀測相位和頻率的高精度估計。文獻［19］提出在星際轉移軌道段可將航天器的運動軌跡簡化為勻加速模型，基于此建模了航天器軌道狀態誤差與其所引起的脈沖TOA偏差之間的關系，并對導航觀測方程進行了修正以消除TOA偏差的影響。但線性化過程或產生高階截斷誤差，且該截斷誤差隨脈沖星觀測周期的增大而增大。所以通常為了將軌道位置誤差進行線性化，選擇壓縮脈沖星觀測周期或將觀測周期分段。如文獻［20］提出將觀測時段劃分為短時段，在每個較短時段內利用針對恒定多普勒頻移模型的相位估計算法估計相位，再借助相位跟蹤的方法提高單段相位估計精度并獲得動態的多普勒頻移估計。文獻［21］提出了由輪廓形變來求解速度誤差引起的多普勒頻移的新思路，定義了輪廓熵以衡量累積輪廓的不同形變程度，推導了存在速度誤差時，頻率偏差與輪廓熵之間的關系，利用最優化方法通過使熵最小（輪廓最為清晰）從而求解出多普勒頻移。該方法本質上仍需要假定在觀測時段內的觀測頻率恒定，即航天器的速度恒定，所以觀測周期不能過大。Anderson和Pines［22］研究了基于鎖相環的脈沖相位跟蹤方法，并給出了針對小流量脈沖星的相位跟蹤方法。文獻［23］將較短觀測時段內的預報位置誤差建模為隨時間近似線性變化，且將這種線性變化的位置誤差對光子到達時間修正的影響建模為恒定的相位偏差加上恒定的多普勒頻移，在此基礎上，提出了一種基于相位和多普勒頻移聯合觀測的X射線脈沖星導航方法，并進行了實驗驗證與分析。以上算法在進行觀測相位與多普勒頻率估計時，未對脈沖星觀測周期的選取進行深入研究。而最優觀測周期的確定對脈沖星導航計算及觀測計劃制定等具有重要的意義，本文對該問題進行研究與討論，以期為觀測方案的制定提供參考。

1 觀測相位估計誤差

最優脈沖星觀測周期是為得到高精度的觀測相位估計，所以將觀測相位估計誤差最小時對應的脈沖星觀測周期稱為最優脈沖星觀測周期。航天器在(t0，tf)的脈沖星觀測周期內，任意時刻的觀測相位［10］為

根據式（1），對?sc(t)的估計誤差取決于對 δr的估計誤差。任意時刻的位置誤差δr為

式中：T為脈沖星觀測周期長度，T=tf?t0；δr0為航天器初始時刻t0的位置誤差。則δr引起的相位誤差δ?為

式中：δ?0為對應t0時刻的初始預測相位。將式（3）展開到2階，表示為

根據上述分析，對δ?的估計將同時存在方差與偏差，采用均方誤差準則，并用mse(δ?)表示δ?的估計均方誤差，則均方誤差mse(δ?)為

式中：var(δ?)為δ?的估計方差；b2為δ?的估計偏差，。方差是由θ的估計方差引起的，所以求出估計方差，即可得到使mse(δ?)最小的T的表達式。

根據文獻［12］，利用探測器探測到的光子到達時間序列，使用最大似然估計可實現對脈沖相位延遲的估計，利用最大似然估計法對θ的估計可表示為

式中：λs、λb分別為脈沖星源的流量與背景流量；h(?)為相位?∈[0，1)的脈沖星的標準輪廓，滿足=1，h(n+?)=h(?)（n為整數）［12］。Emadzadeh證明了利用式（6）的最大似然估計對脈沖相位延遲的估計方差即為克拉美羅界（Cramer-Rao Lower Bound， CRLB）。所以下面推導對θ估計的CRLB。

2 最優脈沖星觀測周期確定

2.1 θ的CRLB推導

任意時刻的相位誤差δ?為

將θ的CRLB表示［13］為

式中：I(θ)為Fisher信息矩陣，根據Emadzadeh和Speyer［13］的結論，I(θ)的第i行第j列元素Iij的表達式為

其中：

由Iij的表達式可得Iij=Iji，所以I為對稱矩陣，且

為確定I(θ)矩陣，需要求I11、I12、I13、I23、I335個元素。Emadzadeh給出了I11、I12、I13的表達式，附錄A給出了I23、I33的推導過程，結果如式（A19）所示。

得到I11、I12、I13、I23、I33的表達式，即可求得的CRLB(θ)。附錄B給出了CRLB(θ)的推導過程。直接求解化解CRLB(θ)難以化解，這里首先化解

式中：a為I(θ)的行列式，將I11、I12、I13、I23、I33代入式（12），化解得到

所以CRLB(δ?d0)=。同理得到

所以

綜上可得

式（17）即為對參數θ估計的CRLB。

2.2 最優觀測周期確定

得 到θ=的CRLB后，可 確 定δ?的估計誤差。根據式（17）、式（4）中δ?的估計方差var(δ?)可表示為

最優觀測周期是指對δ?的估計均方誤差最小時的觀測周期，即所選觀測周期應使式（19）中mse(δ?)最 小。對 式（19）求 極 值，得 到 使mse(δ?)最小的觀測周期的表達式為

至此得到了最優脈沖星觀測周期。需指出，式（20）所定義的最優觀測周期是在式（1）所示的航天器處任意時刻觀測相位模型下推導，以該觀測相位估計誤差最小為準則得到。

3 仿真實驗驗證

為了驗證式（20）的正確性，對同一顆脈沖星在不同觀測周期下進行仿真實驗，并給出仿真的mse(δ?)隨觀測周期變化的曲線，通過對曲線進行擬合，得到最小mse(δ?)對應的觀測周期，并與利用式（20）所預測的最優觀測周期進行對比。

3.1 θ估計方差的仿真

脈沖星觀測信號的仿真是后續實驗的基礎，所以首先需要仿真航天器在脈沖星觀測周期內的脈沖星信號。實驗中采用的軌道根數如表1所示，所使用的脈沖星參數如表2所示。光子TOA仿真方法參考文獻［24］。

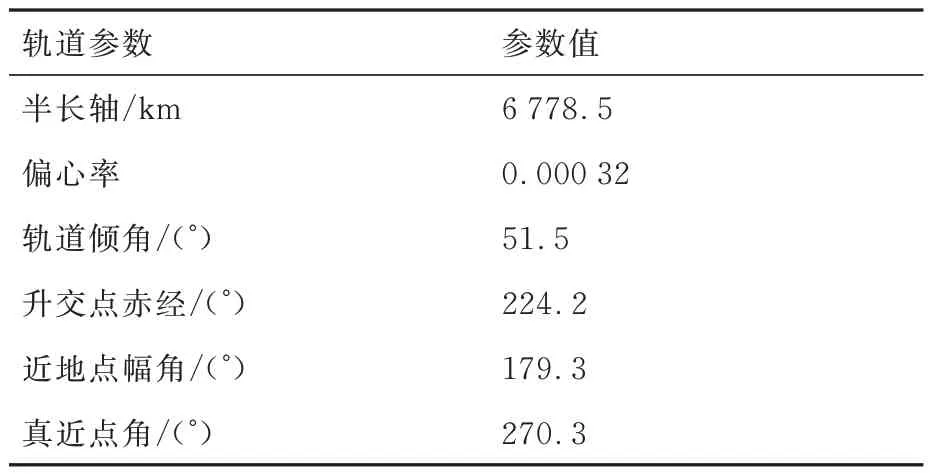
表1 軌道參數Table 1 Orbit parameters

表2 脈沖星參數Table 2 Pulsar parameters

利用上述脈沖星各項參數與軌道進行光子序列仿真，航天器初始的偏差與噪聲方差設置如表3所示。

表3 初始誤差Table 3 Initial error

利用預測位置偏差對光子TOA進行時間校正，得到修正的光子TOA，然后代入式（6）的算法求?。采用利用格點搜索法［25］求式（6），可知求解過程為三維的搜索過程，的3σ搜索 范 圍 分 別 為與。

重復仿真光子TOA，利用每一次仿真的光子TOA進行一次搜索，得到θ的第i次估計值，進 行800次 重 復 試 驗，即i=1，2，…，800。然 后 利 用800次 結 果，可 求 得δ?0、δf0、δf?0的 均 方 誤 差 mse(δ?0)、mse(δf0)、mse(δf?0)。根據式（18）、式（19），可得mse(δ?)的仿真結果為

3.2 不同觀測周期下的mse(δ?)

改變觀測周期，重復3.1節中計算mse(δ?)的步驟，可得到mse(δ?)隨觀測周期變化的曲線。脈沖星PSR B1821-24仿真結果如圖1、圖2所示。

圖1給出了對θ估計的均方根誤差（Root Mean Square Error， RMSE）結果，根據2.1節的推導，CRLB即為對θ估計的RMSE的理論值，根據圖1的仿真結果，的估計均方根誤差隨觀測周期的增加首先逐漸靠近其CRLB，證明推導的θ的CRLB的正確性。但當觀測周期繼續增大，的估計均方根誤差逐漸偏離了CRLB，這是因為對式（3）進行了截斷，且截斷誤差近似以代替，該誤差會隨觀測周期的增加而增大。

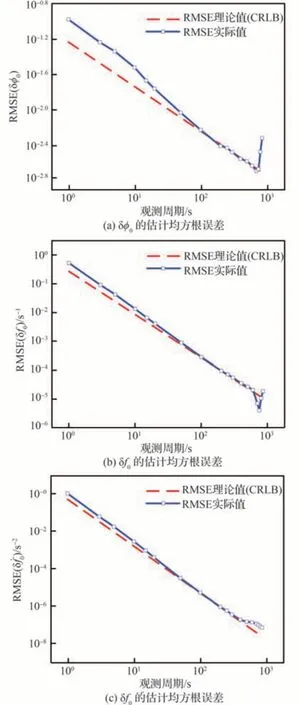
圖1 對θ估計的均方根誤差（PSR B1821-24）Fig. 1 Root mean square error of estimation of θ（PSR B1821-24）

圖2（a）為mse(δ?)隨觀測周期變化的曲線，其橫縱坐標都進行了對數運算。根據仿真結果，mse(δ?)隨觀測周期先減小后增大，且存在使mse(δ?)最小的點，在該點附近擬合，得到圖2（b），根據擬合曲線可明顯看出極小值點的存在，并可得到mse(δ?)最小時對應的觀測周期為620 s，利用式（20）得到仿真條件下的最優觀測周期Topt=673 s，與實驗結果相差53 s，可見預測最優觀測周期在實際最優觀測周期附近，證明了該公式的正確性。

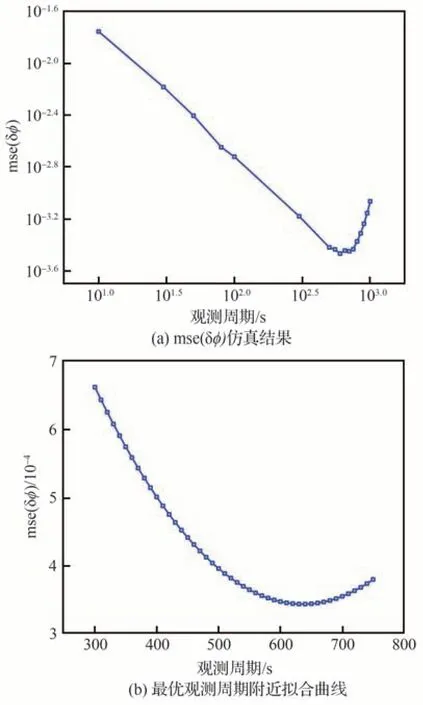
圖2 mse(δ?)隨觀測周期變化曲線（PSR B1821-24）Fig. 2 Curve of mse(δ?) with observation period （PSR B1821-24）

同理，圖3、圖4給出了脈沖星PSR B0531+21的仿真結果。圖3為θ估計的均方根誤差結果，可看出，δ?0、δf0、的估計均方根誤差隨觀測周期的增加首先逐漸靠近其CRLB，證明推導的θ的CRLB的正確性。當觀測周期繼續增大，由于截斷誤差的影響，δ?0、δf0、的估計均方根誤差逐漸偏離了CRLB。

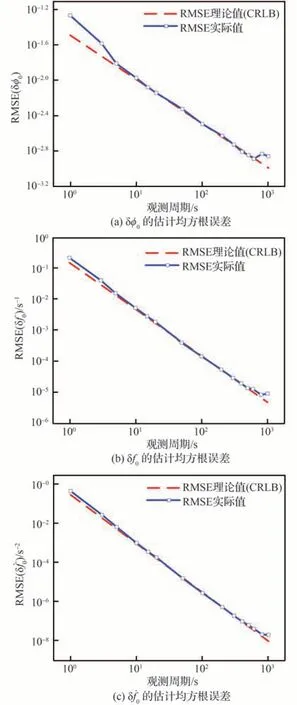
圖3 對θ估計的均方根誤差（PSR B0531+21）Fig. 3 Root mean square error of estimation of θ（PSR B1821-24）

圖4（a）為仿真得到的mse(δ?)隨觀測周期變化的曲線，其橫縱坐標都進行了對數運算。根據仿真結果，mse(δ?)隨觀測周期先減小后增大，且存在使mse(δ?)最小的點；圖4（b）為在最小值附近擬合的結果，曲線的最小值即為仿真得到的最優觀測周期。

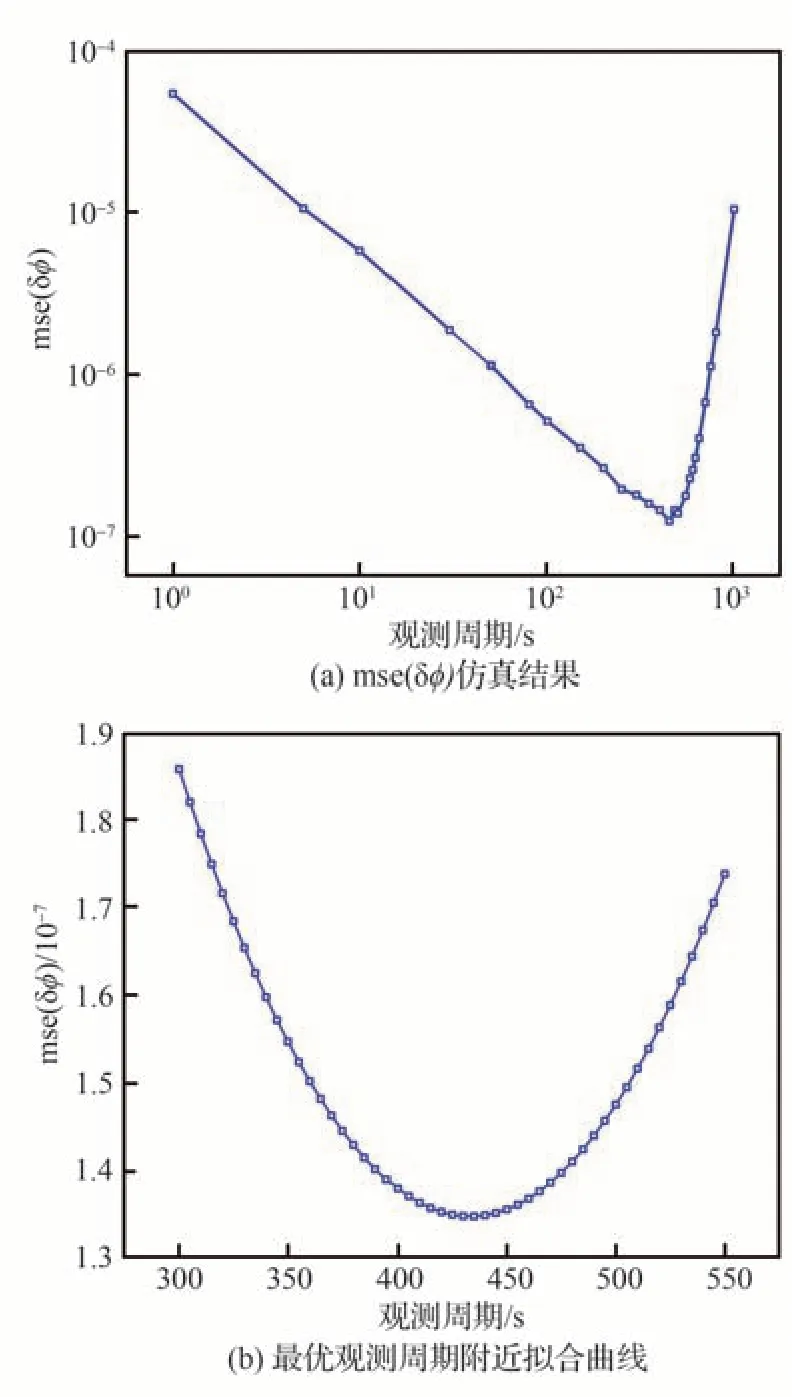
圖4 mse(δ?)隨觀測周期變化曲線（PSR B0531+21）Fig. 4 Curve of mse(δ?) with observation period （PSR B0531+21）

根據擬合曲線可明顯看出極小值點的存在，并可得到mse(δ?)最小時對應的觀測周期為435 s，利用式（20）得到仿真條件下的最優觀測周期391 s，與實驗結果相差44 s，可見預測最優觀測周期在實際最優觀測周期附近，證明了該公式的正確性。

為進一步驗證公式的正確性，使用NICER的實測數據進行了驗證。數據包為“ni1013010142_0mpu7_cl.enents.gz”［26］。該 數據包為PSR B0531+21的實測數據，包含了40279473個光子TOA。表2給出了脈沖星參數信息，軌道根數與表1數據相同。利用該實測數據對θ=進行搜索，并改變觀測周期，重復上述步驟，可得到mse(δ?)隨觀測周期變化的曲線，圖5（a）為mse(δ?)隨觀測周期變化的曲線，其橫縱坐標都進行了對數運算。通過在mse(δ?)最小的點附近擬合，得到擬合結果如圖5（b）所示。

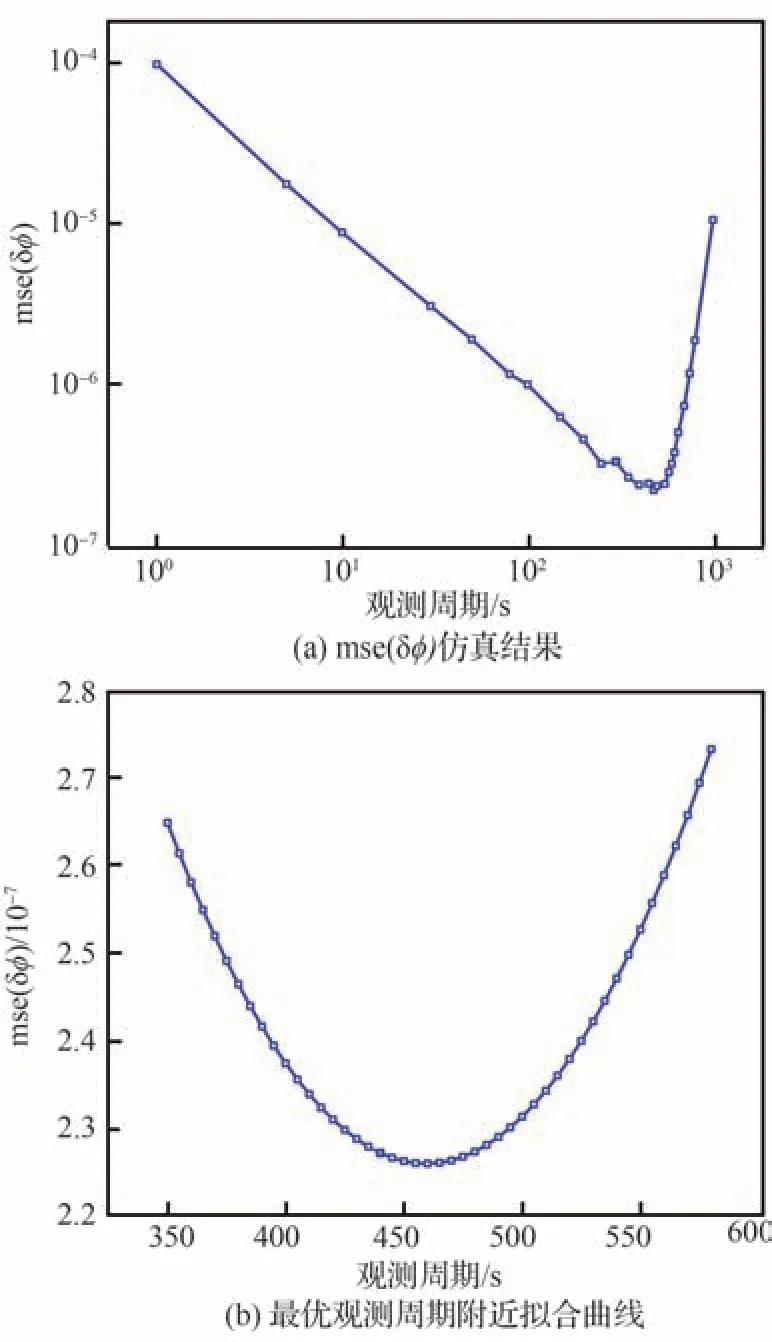
圖5 mse(δ?)隨觀測周期變化曲線（PSR B0531+21實測數據）Fig. 5 Curve of mse(δ?) with observation period （Ob?servational data of PSR B0531+21）

根據擬合曲線可明顯看出極小值點的存在，并可得到mse(δ?)最小時對應的觀測周期為460 s，利用式（20）得到仿最優觀測周期Topt=410 s，與實驗結果相差50 s，可見預測最優觀測周期在實際最優觀測周期附近，且將實測數據的驗證結果與圖4的仿真結果對比，可看出在相同條件下實測數據與仿真數據的結果是接近的，證明了式（20）的可靠性。

使用NICER對PSR B1821-24的觀測數據，進一步進行實驗驗證。數據包名稱為“ni0070010102_0mpu7_cl_t1”“ni0070010103_0mpu7_cl_t1”“ni0070010104_0mpu7_cl_t1”［26］，共19971個光子TOA，結果如圖6所示。

從圖6（a）可看出，mse(δ?)隨觀測周期的變化規律與圖5相同，根據擬合曲線可明顯看出極小值點的存在，并可得到mse(δ?)最小時對應的觀測周期為650 s，利用式（20）得到仿真條件下的最優觀測周期714 s，與實驗結果相差64 s，即預測最優觀測周期在實際最優觀測周期附近，證明了式（20）的正確性。且將實測數據的驗證結果與圖2的仿真結果對比，可看出在相同條件下實測數據與仿真數據的結果接近，證明了所提公式的可靠性。

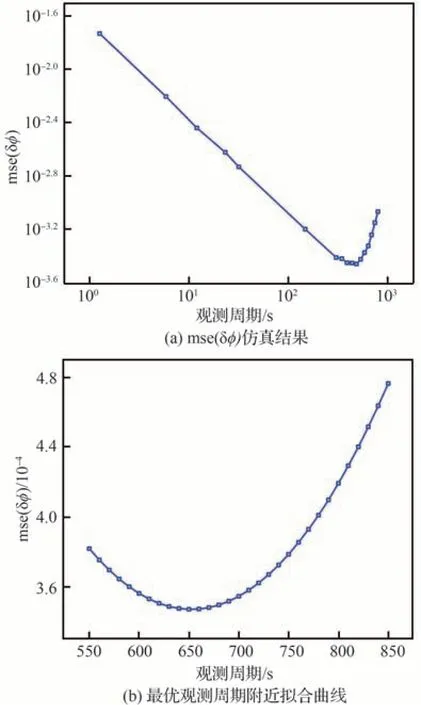
圖6 mse(δ?)隨觀測周期變化曲線（PSR B1821-24實測數據）Fig. 6 Curve of mse(δ?) with observation period （Ob?servational data of PSR B1821-24）

4 結論

在X射線脈沖星導航中，觀測周期的選取是獲得高精度觀測相位估計的關鍵，本文對該問題進行了研究，得到以下主要結論：

1）以航天器處觀測相位估計的均方誤差最小為準則，推導了脈沖星觀測周期與觀測相位估計的均方誤差的關系，給出了最優脈沖星觀測周期的近似計算公式。

2）設計了仿真驗證實驗，仿真結果表明給出的最優觀測周期計算公式對脈沖星PSR B1821-24與PSR B0531+21的預測誤差約為64、44 s，而由脈沖星PSR B0531+21的實測數據得到的預測誤差為50 s，即由該公式給出的最優觀測周期與實驗中對觀測相位估計的均方誤差最小時對應的觀測周期接近，證明所給公式的正確性。

附錄A：

定義

根據Emadzadeh和Speyer［12］的結論，I11、I12、I13可表示為

式中：

以下將推導I23、I33的表達式。

將觀測周期分成N+1段，即

圖A1 觀測周期分段Fig. A1 Observation period segmentation

當n=0，Pn=0，有

將觀測時間分成N+1段，將式（A4）的積分表示為圖A1中每個小區間的積分求和，I23可表示為

根據圖A1，在第n+1個區間內，脈沖星周期為Pn+1，則積分變量t可表示時刻對應的相位?(t)為

將式（A6）代入式（A5），以?為新的積分變量，并利用h的周期性，可化解得到

由于N?1，所以式（A7）中占據主導地位，即

同理，I33的結果為

下面對I23、I33的表達式進行簡化處理。I23的求和項的多項式展開式中，去除包含P0的項，共有項非零項，定義Pˉ23為

相應的，I23、I33可表示為

式中：q23為形如的非零項。所以

綜上，由于N?1，所以可近似認為=0，即。同理可證。

將I11、I12、I13表 示 為I23、I33的 形 式，則I11、I12、I13、I23、I33表達式為

附錄B：

I?1(θ)的求解：根據逆矩陣運算法則，I?1(θ)可表示為

則θ=中的每一個元素的CRLB可表示為