Current bifurcation,reversals and multiple mobility transitions of dipole in alternating electric fields
Wei Du(杜威), Kao Jia(賈考), Zhi-Long Shi(施志龍), and Lin-Ru Nie(聶林如)
Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China
Keywords: dipole,current bifurcation,current reversals,mobility transition
1.Intro duction
Electric dipoles exist universally in various kinds of substances, whose dynamical behaviors in alternating electric fields have stimulated investigators for a long time.It is of great significance in the aspect of utilizing energy for mankind to control their motions.The model describing rotation of dipoles, first proposed by Debye, has also been widely used in many fields such as the interaction between electromagnetic field and matter, the emission and absorption of electromagnetic wave, and the interaction theory between molecules and atoms.For example, the dipole model is used to study the interaction between near-field optical microscopy and samples.[1,2]When studying dielectric and its interaction with the electric field, the electric dipole model is often employed to describe polarization of the dielectric,[3]domain distribution and steering in ferroelectric materials,[4,5]etc.Some research work on electric dipoles has been reported in the existing literature, such as the distribution of electric and magnetic fields excited by dipoles,[6]the interaction between dipole and dipole,[7-9]and movement of dipoles in static field.[10]In addition, the model of dipoles has wide applications to life science.[11]It is believed that theoretical and experimental studies of dipoles will bring about much useful information in many other research fields.[12-14]
The dipoles are usually in materials with spatially periodic potentials.In the alternating electric fields, they can make directed rotation,[15]and motions of the dipoles in the solid often lag behind the change in the electric field, which causes dielectric loss and polarization relaxation.[16-18]In the meantime,they also exhibit many characteristic dynamical behaviors.Abnormal transports of particle in a periodic potential, including absolute negative mobility and current reversal,have been a challenge for a large number of investigations over the years.[19,20]Intrinsic physical mechanism and condition for them to occur have not been understood completely yet, especially for the rotation of the dipoles in the alternating electric fields.In what follows, it will be seen that in the action of the alternating electric fields,the dipole exhibits current bifurcation and multiple current reversals, and multiple mobility transitions.These findings will play important roles in optimizing materials heating and utilizing energy.
In this study,our aims are to investigate anomalous transports of dipole in the two alternating electric fields whose directions are perpendicular to each other, and open up conditions and physical mechanism of the current bifurcation, current reversals, and mobility transitions.This paper is constructed as follows: In Section 2, model and theory are provided.In Section 3,results and discussions are presented.By means of numerical calculations,the anomalous transports of dipoles induced by the external electric field will be analyzed in detail.In Section 4,conclusions are given.
2.Model and theory
Here we consider one-dimensional rotation of a dipole with inertial mass in a constant fieldFc.The fieldFc, for instance,may be a local field produced by some other immobile molecules.As is well known, potential energy of the dipole with momentμ0in the electric fieldFcreads
whereφis the angle between the dipole moment and the electric field.Thus, the differential equation for the dipole with a moment of inertiaI0rotating in the constant electric fieldFcunder the influence of the time dependent fieldsF⊥(t)andF||(t) perpendicular and parallel to the constant fieldFcis given by[21,22]
where the dot aboveφrepresents the first derivative ofφwith respect to timet,andγI0˙φis the damping torque.After dividing Eq.(2) by the angular momentum of inertia, withφ=xwe have
whereγis the damping constant of the dipole rotation, the constantsdis given by
andF⊥(t)andF||(t)are the normalized fields
with the superscript‘un’representing the unnormalized fields in Eq.(2).
For the sake of discussion, we assume that the timedependent fieldsF⊥(t) andF||(t) are the alternating electric fields with the cosine and sine functions
F⊥(t)=A1cos(ω1t), F||(t)=A2sin(ω2t),(6)
whereA1andω1are the amplitude and angular frequency of the normalized fieldF⊥(t), respectively, whileA2andω2are the amplitude and angular frequency of the normalized fieldF||(t).If the constant bias forceFexerting on the dipole is also considered,Eq.(3)can be rewritten as
¨x+γ˙x+dsinx=A1cos(ω1t)cosx-A2sin(ω2t)sinx+F.(7)All these physical quantities and parameters are in dimensionless forms.
In terms of Eq.(7),current of the system is very difficult to be found analytically, yet we can make use of the modified Euler algorithm to calculate numerically its mean angular velocity(or current)of the dipole rotation according to its definition
where〈〉denotes the time average.In the hypothesis of ergodicity,the time average is equal to the ensemble average.Thus the mobility of the dipole can be obtained by
3.Results and discussion
By means of Eqs.(7)-(9), we can calculate numerically current and mobility of the system, and discuss effects of parameters of the alternating fields on movements of the dipole,and the results are plotted in Figs.1-7
3.1.The case of F=0
Let us discuss the case without the external constant bias forceF.As the additional time-varying fieldsF⊥(t)andF||(t)have the same amplitude and angular frequency,i.e.,
Eq.(7)reduces to
Equation(11)can be viewed as the dynamic equation of an inertial particle moving in a periodic potential with traveling wave and basal potentials, where the basal potentialdcosxdepends on the fieldFc.The traveling wave potential is-Asin[ω(t+x/ω)],which describes a traveling wave moving to the negative direction of thex-axis with the velocity-ω.In this case,the velocity of the traveling wave is numerically equal to the angular frequencyωof the additional fields.It is well known that the particle always moves in the same direction as the traveling wave without any signal.[23-27]The dependence of the mean angular velocity〈v〉on the frequencyωof the external fields at different amplitudes of the external fields for the different basal potentialAanddis shown in Fig.1, from which we can see that the external fields greatly affect the dynamical behavior of the dipole.As the amplitude of the basal potentialdequals 0, absolute value of the mean angular velocity first increases and then decreases with the frequency of the external fields increasing,see Fig.1(a).If the amplitudeAis further increased in the case of unchangedd=0,the more prominent two pathways appear in the curves of〈v〉vs.ω, i.e., a current bifurcation phenomenon, see Fig.1(b).The branching point locates atωc?2.68.After the critical point,one of them is that the〈v〉decreases withω,while the〈v〉increases withωfor the other pathway.Furthermore,the dipole almost has the same probability to occupy the two pathways.During the branching region,it can possess two values of〈v〉.This is similar to the optical bistability.[28,29]By comparing Figs.1(a)and 1(b),when the amplitude of the external fields increases, a current bifurcation of the dipole will occur at the larger frequency and the bifurcation area will be larger.
However, if theAis fixed at the value 3 in the presence of the basal potential (d=1), absolute value of the〈v〉first increases,then suddenly drops to zero,i.e.,a current transition phenomenon appears,see Fig.1(c).The inflection point takes place atωin≈2.05.The phenomenon can be explained like this: For smaller wave velocity, the dipole stays in its potential well and moves with the wave together.Thus,the average angular velocity of the dipole increases linearly with the angular frequency of the alternating field increasing.Due to the action of the basal potential, its average angular velocity is smaller than its wave velocity.As the frequency of the alternating electric field increases, it is difficult for the dipole to keep pace with the wave for its inertia and friction,and the angular velocity of the dipole should decrease gradually like that in Fig.1(a).For the barrier in the basal potential,the average angular velocity suddenly falls to zero.Yet, as the amplitude of the basal potentiald=1 remains unchanged and the amplitude of the alternating electric fields is increased to 5, the larger area bistable state and inflection point phenomena take place simultaneously in the system, see Fig.1(d).Therefore it can be concluded that the alternating electric fields play important roles in inducing current bifurcation and current transition.

Fig.1.The mean angular velocity〈v〉vs. ω at different amplitudes of the alternating electric fields: A=3,5, and different amplitudes of the basal potential: d =0, 1.The other parameters are γ =0.9, and time step 0.001.Initial conditions are t=0,x=0,and dx/dt=0.
Let us discuss the case ofω1/=ω2,namely,the frequencies of the alternating electric fields perpendicular and parallel to the constant field are not equal to each other.Figure 2 is the time evolutions of the dipole angular positionxat different parametersω2=0.2,0.25,0.4,1.0,1.5,withω1=1.The trajectories in Fig.2 are very close to straight lines,which indicates that the dipole has been stable state of non-equilibrium within the evolution time.Thus, their slopes represent angular velocities of the dipole.From Fig.2, we can easily see that the mean angular velocity〈v〉is affected greatly by the angular frequencyω2of the normalized fieldF||(t).Due to the temporal symmetry breaking byω1/=ω2,〈v〉is less than zero atω2=0.2.Asω2increases, the dipole begins to rotate to positive direction.However, forω2=1.0, the dipole rotates in a negative direction again.It is interesting that the dipole experiences many times of direction changes from negative→positive→negative→positive withω2increasing.This means that there exists multiple current reversals in the system.[30-32]
In order to catch some insight into the multiple current reversals,the dependence of〈v〉onω2at different angular frequenciesω1of normalized fieldF⊥(t)is shown in Fig.3.Figure 3 looks very rough, but the data in it are actually correct and reliable because the time evolutions of some typical samples in Fig.2 are very straight, or the dipole has been stable state of non-equilibrium.It can be seen from Fig.3 that the multiple current reversals rely on the frequency to a large degree.Asω1=0.8, 1.0, or 1.6, the〈v〉changes its sign many times,i.e.,multiple current reversals.Nevertheless,as theω2increases(e.g.,ω2=3), the multiple current reversals gradually disappear,and the current of the system turns to be zero.Because the system’s symmetry is broken temporally by the two periodic signals, and its symmetry depends on the frequenciesω1andω2.Asω2takes greater value, the signalAsin(ω2t)changes so fast that the system does not keep pace with it.Thus, function of the signal is lost, and the system is temporally symmetric,which leads to its current being zero.

Fig.2.Time evolutions of x at different frequencies of the normalized field F||(t): ω2=0.2,0.25,0.4,1.0,1.5,with A1=A2=A=2,ω1=1,d=1.The other parameters are the same as those in Fig.1.

Fig.3.The mean angular velocity〈v〉vs. ω2 at different frequencies of the normalized field F⊥(t):ω1=0.8,1.0,1.6.The other parameters are the same as those in Fig.2.
3.2.The case of F/=0
As the external constant bias forceFis exerted on the dipole,the system will also display some interesting dynamical behaviors.
Figure 4(a) shows the〈v〉vs.the constant bias forceFat different amplitudes of the alternating electric fields:A1=A2=A=1,2,3,4,5,withω1=ω2=1,d=1.From Fig.4(a),we can see that the amplitudes of the alternating electric fields actually affect transport of the dipole.AsA1=A2=A=1,the dipole remains stationary untilFis greater than about 1.This is because the traveling force in Eq.(11)is too small to make the particle jump over the basal potential barrier (d=1).AsFis just greater than the threshold value,the dipole suddenly rotates with the angular velocity 1,then increases linearly withFincreasing.With the increment ofA(e.g.,2),the three platforms〈v〉=-1,-0.25,0 appear in the curve of〈v〉vs.F.According to the total potentialdcosx-Asin[ω(t+x/ω)]-Fx,the two platforms〈v〉=-1,0 should come from the traveling potential-Asin[ω(t+x/ω)]and the basal potentialdcosx,respectively,while the platform〈v〉=-0.25 from the co-action between the two types of potentials.AsAis further increased(e.g., 3, 4, 5), the system comes back to one platform caused by the traveling potential,whose〈v〉takes-1.After the platforms, the particle’s velocity also suddenly jumps to certain positive value, then varies linearly withF.Transport of the system becomes normal.The greater the valueAtakes, the greater the transition force is.Fig.4(b)is the mobilityμvs.Fcorresponding to Fig.4(a).It can be seen easily from Fig.4(b)that the mobility obviously transits twice at least forA=2,while only once forA=1,3,4,5.

Fig.4.Behavior of〈v〉vs.the constant bias force F for(a),and the mobility μ vs. F for(b)at different amplitudes of the alternating electric fields: A1=A2=A=1,2,3,4,5,with ω1=ω2=1,d=1.The other parameters are the same as those in Fig.1.
Of course, frequency of the traveling force in Eq.(11)also influences the mobility transition effect.Figure 5 is the dependence of〈v〉onFat different frequencies of the alternating electric fields withA1=A2=A=2,d=1.We can see that for the smaller frequencies (e.g.,ω1=ω2=0.25),there are four platforms in the curve of〈v〉vs.F.In other words, the mobility transits four times.With the increment of the frequencies,the number of the platforms gradually decreases.For greater frequencies(e.g.,ω1=ω2=10),the traveling force loses its function,so only the platform〈v〉=0 takes place due to the basal potential.
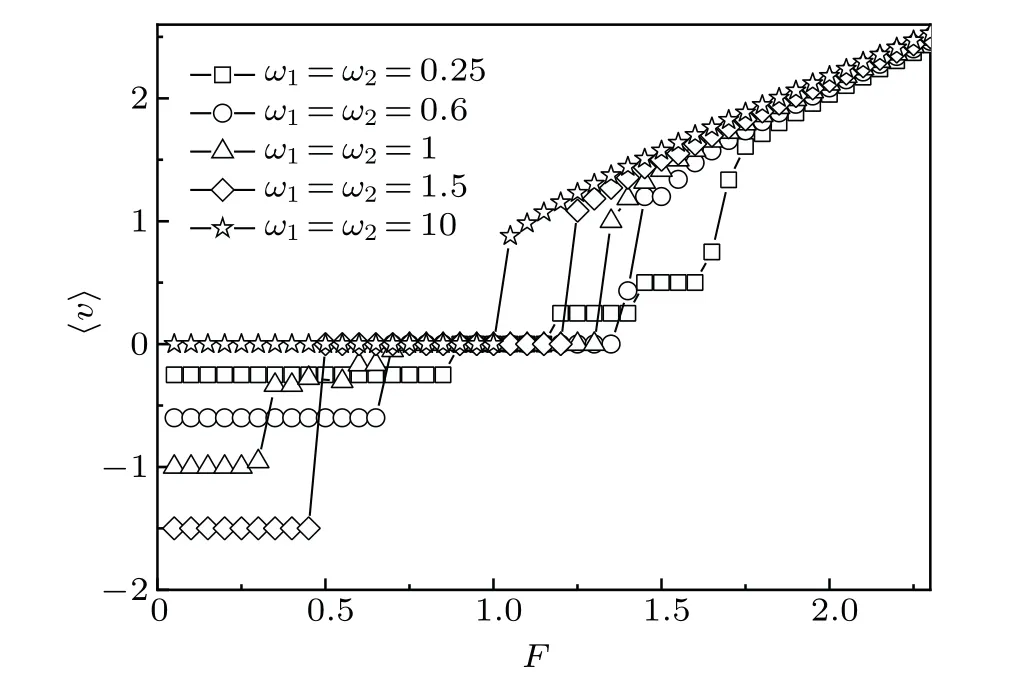
Fig.5.Behavior of〈v〉vs. F at different frequencies of the alternating electric fields: ω1=ω2=0.25,0.6,1,1.5,10,with A1=A2=A=2,d=1.The other parameters are the same as those in Fig.1.

Fig.6.Behavior of〈v〉vs. F at different values of ω2: 1.5,2,3 for(a),5 for(b),with ω1 =1,A1 =A2 =A=2,d=1.The other parameters are the same as those in Fig.1.
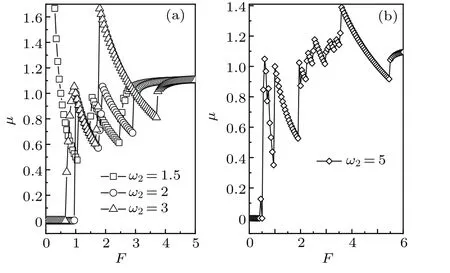
Fig.7.Behavior ofμ vs. F at different values of ω2: 1.5,2,3 for(a),5 for(b),with ω1=1,A1=A2=A=2,d=1.The other parameters are the same as those in Fig.1.
Let us discuss the mobility transitions in the case ofω1/=ω2.The dependence of〈v〉onFatω2=1.5,2,3,5 andω1=1 is shown in Fig.6.Figure 6 indicates that there still exist many mean angular velocity platforms in this case, where the two platforms〈v〉=ω1and〈v〉=ω2are indispensable at least.Nevertheless,asω2=5 andω1=1,seven obvious mean velocity platforms occur in the system.This makes dynamical behavior of the system more inconceivable.Thus,mobility of the system in this case transits more times compared with that ofω1=ω2due to the action of more types of traveling forces,see Fig.7.
4.Conclusions
In summary, we have investigated the characteristic dynamical behaviors of the one-dimensional dipole in the action of the two alternating electric fields whose directions are perpendicular to each other.Our numerical results show that the two alternating electric fields play crucial roles in inducing abnormal dynamical behaviors of the dipole.As the two alternating electric fields are periodic functions of cosine and sine with the same amplitude and frequency, there exists current bifurcation phenomenon about the frequency.If the frequencies of the two alternating electric fields are not equal to each other,they can cause the multiple current reversals of the dipole.As a constant bias force exerts on the diploe,there are many current platforms appearing in the curve of〈v〉vs.F.Namely,multiple mobility transitions take place in the system, which depends on amplitudes,frequencies and number of the traveling forces in it.
Here the effects of the alternating electric fields on the dynamical behaviors of the dipole are considered.It is found that there exist current bifurcation,reversals and multiple mobility transitions phenomena in the system.The findings not only help us further understand dynamical behaviors of the dipoles in the alternating fields, but also play important roles in enhancing heating efficiency of matter, which are of important significance for saving energy sources.According to our research results,one can optimize matter heating through adjusting amplitudes and frequency of the exerted alternating fields.
Acknowledgements
Project supported by the Research Group of Nonequilibrium Statistics (Grant No.14078206), and Kunming University of Science and Technology,China.
- Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA

