Realization of the iSWAP-like gate among the superconducting qutrits

Peng Xu(許鵬), Ran Zhang(張然), and Sheng-Mei Zhao(趙生妹)

Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Keywords: circuit quantum electrodynamics(circuit QED),superconducting qutrit,iSWAP-like gate

1.Introduction

Based on the intrinsic properties of the quantum mechanical systems, such as quantum interference, quantum processors can solve many troublesome tasks which classical computers cannot.[1-4]With the rapid developments in the engineering and controlling of the quantum systems,the investigations of quantum processors have begun from single isolated quantum systems toward multiqubit quantum processors.[5-7]Through scaling up to more qubits together,it has entered the noisy intermediate-scale quantum (NISQ) era.[8]A 53-qubit programmable superconducting quantum processor has been demonstrated to promise significant advantages for a hard task, achieving the quantum supremacy.[9]The prospect of demonstrating quantum supremacy with NISQ processors relies critically on extending quantum system size and the implementation of fast,high-fidelity quantum gate operations.[10-12]Generally,to implement universal quantum control,the quantum gate operations[13]should include the single-qubit gates and two-qubit entanglement gates, such as the controllednot (CNOT) gate, the controlled-phase (CZ) gate, and the iSWAP gate.Over the past decades, all these quantum gates have been widely applied in quantum information processing schemes, such as quantum computation,[14-17]quantum error correction,[18-21]and quantum cryptography.[22-24]

Conventional quantum information processing only involves the lowest two energy levels of quantum systems,which are traditionally defined as qubits.However, the quantum processors based on the qutrits[25]or qudits (quantumd-level systems)[26]have exhibited significant advantages and have found important applications in speeding up quantum gates,[27]improving qubit readout,[28]higher encoding capabilities,[29,30]and realizing quantum algorithms.[31,32]In the era of high-fidelity magic state distillation,[33]more robust quantum cryptography protocols,[34,35]and quantum error correction,[36]multi-level quantum systems have been shown useful with small code sizes.Based on the advantages, highdimensional states have also been exploited in superconducting quantum processors, such as the use of the higher levels for qubit readout[37]and spin-1 quantum simulation.[30]For example, qubit rotations can be realized through stimulated Raman adiabatic passage with a three-level Λ configuration consisting of two computational states with an auxiliary state.[38,39]The arbitrary rotation and entanglement in the three-level Λ-type flux qutrits have also been discussed.[40]A scheme for the coherent population transfer between uncoupled or weakly coupled states in ladder-type superconducting transmon qutrits has been proposed.[41]More recently,the implementation of high-fidelity single-or two-qutrit gates has attracted much more attention.[42-44]And the fast and precise quantum control beyond the two-level system can pave the way to extend quantum computation and study highdimensional quantum physics.For superconducting quantum information processing, many optimal strategies have been proposed to realize the quantum gate with fidelities exceed 99%.[45-50]Particularly, the iSWAP gate has become a key topic in scalable quantum computation.And it will naturally occur in a quantum system withXYinteraction or the Heisenberg models,e.g.,superconducting circuits[51]and solid-state qubits.[52,53]

In this work,we propose a scheme to realize an iSWAPlike gate which can be denoted as

in a frequency-tunable,fixed-coupling superconducting qutritbased system.This system consists of twoΞ-type energy-level superconducting qutrits that are coupled via a superconducting resonator.The anharmonicity for the two qutrits can differ,such as the weakly nonlinear transmon and strong nonlinear flux qutrits.[41,54,55]Unlike the computational states traditionally defined in the two lowest energy levels, we shall use the ground state and the second excited state of qutrits.The two qutrits’populations can be swapped by tuning their transition frequencies into resonance.By designing the frequency pulse profile and optimizing control parameters, the fidelity of the iSWAP-like gate can be as high as 99.85%.The proposed quantum system can be scaled up to multi-qutrit cases and may be useful for quantum computing in the NISQ era.

The remainder of this paper is organized as follows.Section 2 describes the physical model and analyzes the dynamical evolution.After introducing the superconducting qutrits architecture, we investigate the realization of the iSWAP-like gate and the fidelity with experiment feasible parameters in Section 3.Finally,in Section 4,we present the conclusions of our study.

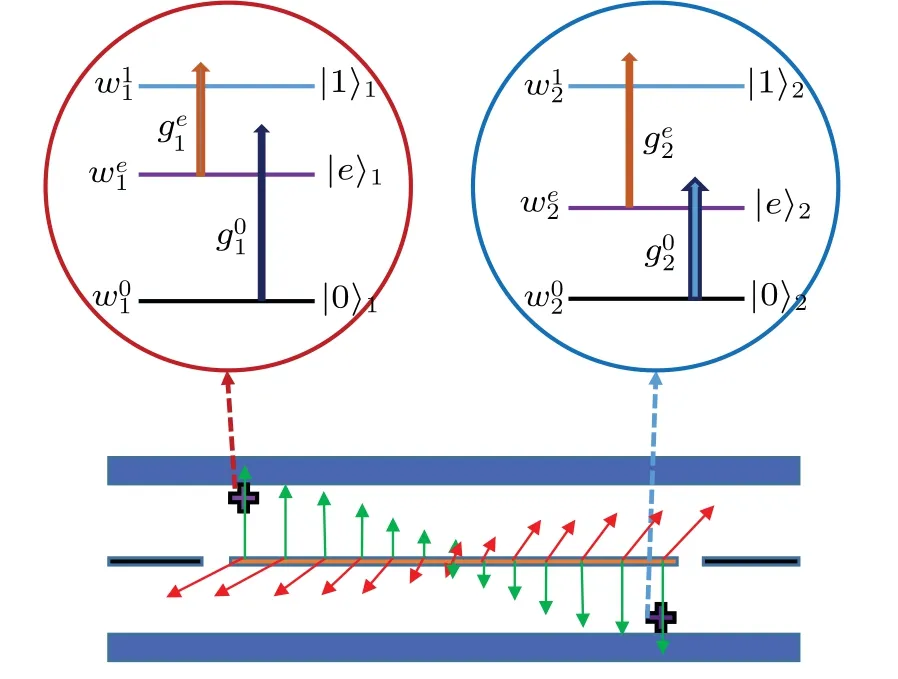
Fig.1.Circuit QED schematic consists of two superconducting qutrits coupled to a resonator.The Ξ-type levels of qubit-l comprise an auxiliary state |e〉 and two computational states |0〉, |1〉 in the above circles.The anharmonicity defined as(w1l -wel)-(wel -w0l)for the two qutrits is different (α1 ＆lt;0 and α2 ＆gt;0) and the qutrits-resonator coupling strength is fixed.

2.The physical model

The quantum system comprises two superconducting qutrits that are coupled via a superconducting resonator, as shown in Fig.1.We consider that the superconducting qutrits with negative anharmonicity can be denoted asQ1and the capacitively shunted flux qutrit with positive anharmonicity is depicted byQ2.[49,56-58]For simplicity, we assume only one related mode of the resonator interacts with the two qutrits,and the qutrit-resonator detuning is much larger than that of their coupling strength.Considering the rotating wave approximation, based on the bare eigenstates, the system can be described by the Hamiltonian(hereafter ˉh=1)

Before discuss the implementation of the iSWAP-like gate, we first analyze the dynamical evolutiuons of the quantum system.The system is initialized in the state|010〉c12(or|001〉c12) where theQcis in the vacuum state|0〉, theQ1is prepared in the state|1〉(or|0〉),andQ2is in the state|0〉(or|1〉).According to the Hamiltonian in Eq.(2),the whole quantum system will evolve within a subspace which is spanned by five basis states|010〉c12,|1e0〉c12,|0ee〉c12,|10e〉c12, and|001〉c12.As described above, we assume that the computational states are the ground state|0〉and the second excited state|1〉.The iSWAP-like gate is betweenQ1andQ2, and theQconly mediates the interaction between the two qutrits.From state|010〉c12,we can give the following transition path,which enables the interaction between|010〉?|001〉,

At first glance,the perfect population swaps between the states|10〉12and|01〉12seem insuperable in a fixed-coupling architecture.However, through tuning one of the qutrits into and out of particular resonance conditions,the interactions can be controlled.[31,59]The approach is sensitive to the frequency of crowding as they should avoid unwanted crossing during the gate operations.The key to this approach is to minimize the swap and leakage errors.The swap error is the residual swap population, and the leakage error can be given by the probability to occupy the non-computational states in the leakage channel.Considering the five-state subspace described above,the swap channel comprises states|010〉c12and|001〉c12, and the leakage channel comprises|1e0〉c12,|0ee〉c12,and|10e〉c12.Based on the designed frequency pulse profile,we can realize a full population swap by sweeping the controlled frequency.To obtain a complete swap,we need to optimize the pulse-shape parameters by measuring probabilities of states|10〉12and|01〉12.By using the fourth-order perturbation theory[60-62]or a unitary transformation,[63,64]we can obtain the effective Hamiltonian(in the interaction picture),

Additionally, the key to performing the high-fidelity iSWAP-like gate also lies in the system parameters.The anharmonicity of the qutrits is an essential factor that determines the effective interacting strength.Here, we focus on the experiment accessible systemic parameters with anharmonicitiesα1/2π=-300 MHz,α2/2π=700 MHz, and the frequencies forQ2andQcarewe2/2π= 4.6 GHz,wc/2π=6.0 GHz.The qutrit-resonator coupling strengths are fixed asg01/2π=90 MHz andg02/2π=120 MHz, respectively.To achieve a population swap between states|10〉12and|01〉12,the present scheme requires tuning the qutrits into the resonant.Here, we fix theQ2’s frequency, and only tune the frequencywe1ofQ1from the idling pointwidl/2π= 4.7 GHz to the working point.However, the unwanted crossings are unavoidably swept past or brought near when tuning the frequencies.To check all the wanted or unwanted crossing, we first demonstrate the energy level diagram during the linear variation of frequencywe1, as shown in Fig.2.One can find that there are two avoided crossings associated with the interactions|010〉c12?|0ee〉c12,|010〉c12?|001〉c12(from left to right).The interaction|010〉c12?|0ee〉c12is the unwanted one, while the|010〉c12?|001〉c12is the wanted interaction for implementing the iSWAP-like gate between the two qutrits.The resonance between|010〉c12and|001〉c12will occur at～5.08 GHz that indicated by black-dotted line with arrow in Fig.2.Furthermore, as predicted in Fig.2, the bare frequencies will be shifted owing to the interaction terms.It is the key point to realize the high-fidelity iSWAP-like gate during the procedure of tuning the frequency of qutrit from the idle point to the working point.Consequently, one needs to include a small overshootΔoverthat acts as a fine-tuning parameter to account for the control pulse non-idealities.The avoided crossing interaction|010〉c12?|001〉c12illustrates that the optimal control pulse for the frequencywe1can enable a complete swap between|10〉12and|01〉12.And the typical working point is around 5.08 GHz within the experiment accessible parameter ranges.

Fig.2.The energies of the eigenstates for the systemic Hamiltonian in Eq.(2) as a function of the Q1 frequency we1.Here, the anharmonicities α1/2π =-300 MHz, α2/2π =700 MHz, and coupling strength g01/2π=90 MHz and g02/2π=120 MHz.The Q2’s frequency we2/2π=4.6 GHz and the frequency of resonator is wc/2π = 6.0 GHz.The black-dotted line with arrow denotes the wanted interaction between|010〉c12 and|001〉c12 that occurs around the frequency ～5.08 GHz.

3.Realization of iSWAP-like gate

The above discussions imply that the high-fidelity iSWAP-like gate can be realized by experimentally designing the frequency-tunable pulse shape with accessible systemic parameters.To realize a complete population swap between the states|10〉12and|01〉12and avoid the gate errors, the frequency pulse profile should be designed carefully.

In the following, we will give a detailed description of the iSWAP-like gate.For simplicity, the (bare) frequencies of theQ2andQcare assumed to be fixed.As discussed in Section 2, the key idea behind our approach is designing the frequency pulse profile and tuning the frequency ofQ1to the working point, as shown by the black-dotted line with arrow in Fig.2.When tuning the system near this working point,the populations swap between states|10〉12and|01〉12will occur.However, a complete swap needs theQ1to remain in the interaction frequency with an appropriate gate time.Combining the qubit frequency modulation and gate time control,we consider frequency pulse profile,as suggested in Refs.[65,66],

wherewidlandwgateare the idling and working frequencies that decide the off or near resonance for the two qutrits.The parameterσis the standard deviation of the Gaussians which determines the pulse switching time,and the value oftrampwill determine how the pulse is truncated att=0 andtgate.For simplicity,we assume that there is a definite relationship between themtramp=cσwithcis an optional constant.Thetgateis the hold time that makes sure the implementation of gate operation.

Fig.3.Numerical results for the population swap vs.the overshoot frequency Δover and gate time tgate.The population of states |001〉c12(a) and |010〉c12 (b).The system is initialized in state |010〉c12, the frequency of Q1 varies according to the pulse shape given in Eq.(6)with widl/2π = 4.7 GHz, wgate/2π = 5.1 GHz, σ = 1/30 ns, and tramp =6√σ.The other systemic parameters used are same as in the Fig.2.The red squares in (a) and (b) indicate the optimal parameters for achieving minimum gate error.

As described above,the overshoot frequencyΔoveris also one of the critical factors to minimize the gate error for the implementation quantum gate.[67]Therefore,to enable a complete population swap, we should include an additional small overshoot to the interaction frequencywgatewhich serves as a fine-tuning parameter to account for the dressed eigenbasis due to the small residual coupling before and after the gate operation.According to interaction conditionw11+Δover?w12in the current quantum system,we can evaluate a finite region for the overshoot frequencyΔover.Applying time-dependent control pulse given in Eq.(6),we scan the qubit frequencyw1efrom its idling point to the working point back and forth for different gate timetgate.We can find the optimal parameters by measuring the wanted probabilities during the sweep process.

The above results illustrate that the optimal gate time and overshoot frequency values can be picked out from the parameters map after choosing a suitable interaction frequency.To demonstrate the performance of the iSWAP-like gate with the optimal parametersΔoverandtgate,we simulate the dynamical evolution under the Hamiltonian in Eq.(2),as shown in Fig.4.In Fig.4(a), we plot the control frequency pulsew1e,1(t) with the optimal values picked out from the two-dimensional scans in Fig.3.To avoid leakage into the non-computational state|0ee〉,a short switching timeσ=1/30 ns is applied.The control frequency is almost a rectangular pulse of durationtgate.The inset of Fig.4(a) indicates that a small overshoot frequency can compensate the little difference betweenw11andw12.When theQ1frequencywe1(t) is tuned back to the idle point 4.7 GHz (far away from the interaction frequency), the populations swap between the states|01〉12and|10〉12will be turned off.

The results given in Fig.4(b)show that the exchange interaction|01〉12?|10〉12is achievable with experimentally accessible parameters.The leakage error to the unwanted states will occur during the swap process.In particular, the leakage to state|0ee〉c12(solid green line in Fig.4(b))is very conspicuous during the gate operation.This is because the system will pass through the parasitic resonance point associated with the interaction|010〉?|0ee〉, as shown in Fig.2.In addition, it shows dips every～5 ns,and the minimum error can be suppressed to 4×10-4through controlling the gate timetgate?198 ns precisely.Based on the digital-to-analog chips, the control can be operated within 1 ns.[68]And subnanosecond resolution can also be obtained by discretizing the control pulse.The leakage to states|10e〉c12and|1e0〉c12remain at 1.5×10-5and 4×10-4which are small enough to be ignored.The swap error is approximately 1.2×10-5.To emphasize the important role of overshoot frequency, we also plot the dynamical evolution withΔover/2π=12 MHz in Fig.4(c).We can find the uncomplete swap occurs, this further shows that the overshoot is critical to optimizing the gate performance.In Figs.4(b) and 4(c), we also plot the sum of all the five-state populations(cyan-blue solid lines).It further demonstrates that the dynamics is confined in the subspace presented above.

Fig.4.System dynamics for implementing the iSWAP-like gate with the optimal values for Δover and tgate chosen from the map in Fig.2(a).Typical control pulse defined in Eq.(6).(b)State populations during the gate operation for the two-qutrit system initialized in state|010〉c12 with the overshoot of Δover/2π =12.22 MHz and the gate length tgate ?198 ns.(c)Same as in(b),instead showing the results with the overshoot of 12 MHz.

Having found the optimal parameters for the realization of the iSWAP-like gate in Fig.4,we now turn to quantify the fidelity of the gate.The generic two-qubit unitary operation for the iSWAP-like gate is given by[67]

where specifying the swap angleθ, conditional phaseφ,and the single-qubit phasesδ1,2,3.Here we considerθ=π.To quantify the performance of the implemented iSWAP-like gate,we consider metric of state-average gate fidelity defined as[69]

whereUrealis the actual evolution operator (without considering the effect of decoherence).This is evaluated based on the full system Hamiltonian given in Eq.(2).By optimizing the four angles, we can obtain the high-fidelity iSWAPlike gate.Considering the single-qubit phasesδ1=-0.0424 rad,δ2=-0.0422 rad,δ3=-1.5887 rad, and conditional phaseφ=-2.5835 rad,we find that the average gate fidelityF=99.85% with the gate operation time～198 ns.For the single-qubit phase, one can implement the sing-qubit phase operations[66,70,71]right before and after the iSWAP-like gate,correcting the single-qubit local phases.As the state-of-theart experiments of superconducting quantum systems report decoherence times[72,73]that can far exceed the gate operation time.Thus, we have neglected the effect of decoherence and decay from the system.The presented scheme can also be applied for Λ-type qutrits with the lowest two energy levels as the computational states and the same-sign anharmonicity cases.

4.Conclusion

We present a scheme to realize an iSWAP-like gate withΞ-type qutrits.The quantum system consists of two superconducting qutrits with opposite-sign anharmonicity coupled to a superconducting resonator.By tuning the frequency of one qutrit from the idling point to the working point in terms of the designed pulse profile,the iSWAP-like gate can be finished within～198 ns.With the experimentally accessible parameters,we demonstrate that it is possible to obtain an intrinsic average fidelity of 99.85%.Moreover,in principle,the remained gate errors can be further reduced by using the synchronization scheme,[67]which involves the optimization of working frequencies of the two qutrits.The different truncated energy levels of the resonator will affect the realization of the iSWAP-like gate in the presented model.But,through our proposed method,we can always find the optimal parameters(the frequency of overshoot and gate time)for the tuning of qutrit to implement the high-fidelity operation of iSWAP-like.Additionally,the presented protocol can also be utilized for superconducting qutrits with same-sign (both positive or negative)anharmonicities.Using the current technology,we expect that our approach can also be extended to enable the construction of high-fidelity multibody gates operation as well.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.12105146 and 12175104), and sponsored by NUPTSF (Grant No.NY220178).S.M.Z.was supported by the National Natural Science Foundation of China(Grant No.61871234).