寬包線吸氣式高超聲速飛行器外形優化研究

王健磊，牟 桓，魏 震，王 強，龔春林，*

(1.西北工業大學 航天學院，陜西省空天飛行器設計重點實驗室，西安 710072；2.北京機電工程研究所，北京 100074)

0 引言

高超聲速飛行器的動力系統一般采用吸氣式發動機或組合推進系統。與傳統的化學火箭相比，吸氣式發動機以大氣中的氧作為氧化劑，大大降低了飛行器的重量[1]。吸氣式高超聲速飛行器具有飛行速域寬、比沖高、推重比大等優點，目前適用的動力系統主要有火箭基組合循環動力系統（rocket based combined cycle,RBCC）[2]、渦輪基組合循環動力系統（turbo based combined cycle,TBCC）[3]、空氣渦輪火箭發動機（air turbo rocket,ATR）[4]、渦輪輔助火箭增強沖壓組合循環發動機（turbo-aided rocket-augmented ram-jet combined cycle engine,TRRE）[5]等。組合動力系統將不同的動力模態有機組合在一起并將彼此的優勢結合，拓展了飛行器的飛行速域與空域[6]。

在吸氣式寬包線高超聲速飛行器設計所涉及的學科中，氣動設計能夠直接影響飛行器的飛行性能和飛行品質，對飛行安全、飛行效率與經濟性等都具有決定性的影響。為了使飛行器具有良好的氣動特性，氣動外形優化是高超聲速飛行器設計中面臨的關鍵問題之一，國內外在該方面做了大量的研究。在國外，Takahiro 和Takeshi[7]對兩級入軌RBCC 運載器進行了多學科優化設計，在氣動模塊上通過工程估算法來計算樣本點氣動特性并建立了RBF 代理模型，最后利用模擬退火算法來獲取全局最優外形；Atsushi 等[8]基于三維Euler 方程以及序列二次規劃算法對巡航點處的高超聲速飛行器外形進行了優化，優化時將亞聲速、跨聲速兩個設計點的氣動性能作為約束條件，同時也考慮了防熱、結構等其他學科約束，得到了較為理想的構型；Ahuja 和Hartfield[9]通過高速面元法求解巡航時高超聲速飛行器的氣動特性并利用準一維流來模擬發動機內流，實現了氣動、推進、結構學科的匹配優化。在國內，車競[10]以吸氣式高超聲速巡航飛行器為研究對象，利用多目標遺傳算法，以巡航飛行階段的氣動力、氣動熱、雷達散射截面等作為優化目標，對高超聲速飛行器氣動布局的機身與機翼分別進行單獨優化和總體優化；李曉宇[11]等對吸氣式高超聲速飛行器進行參數化建模，采用高精度CFD 方法建立了氣動響應面近似模型，并結合遺傳算法獲得了不同優化目標的優化外形；陳兵[12]總結了吸氣式高超聲速飛行器的一體化設計與分析方法，運用多點優化的手段對寬速域RBCC 運載器的外形進行了分部件優化與整機優化，最后通過彈道驗證證明了優化方案的優越性，但在整機優化時未使用基于N-S 方程的三維CFD 分析。綜上所述，國內外對于吸氣式寬包線高超聲速飛行器氣動優化設計研究目前主要集中在分部件優化與機體/推進一體化設計；在氣動分析手段上，飛行器全機優化往往采用工程估算法，一定程度上影響了優化結果的可靠性；在評估點選取上，以單點優化為主，滿足不了工程實際的需要；在優化策略上，以全局或局部范圍內的單輪優化為主，無法保證優化結果的全局最優性。因此對于吸氣式寬包線高超聲速飛行器，基于三維高精度CFD 手段且考慮多評估點的多層氣動優化仍需要進一步研究。

針對本文的優化問題，確立了如圖1 所示的包含基于自適應代理模型的全局優化和基于伴隨梯度法的局部優化的兩層優化思路。寬包線氣動優化問題往往是非線性、多峰值的，使用梯度算法容易陷入局部最優。使用代理模型來代替真實模型可以減少需要計算的樣本點數目，但代理模型需要大量的樣本點訓練才能達到較高的精度，這對于本文的氣動優化問題來說仍是不可承受的。因此，本文提出一個折中方案：首先利用略低于平均精度水平的代理模型得到初步優化方案，在此基礎上通過梯度算法進行局部尋優。第一步優化代理模型的精度不需要太高，這樣能有效減少訓練樣本點的數目。第二步優化求解目標函數與設計變量的梯度時采用了離散伴隨方法，該方法的計算量與設計變量個數無關，可大大提高梯度求解效率[13-14]。因此，該優化策略既能有效降低氣動計算量，又能得到相對精確的優化解。

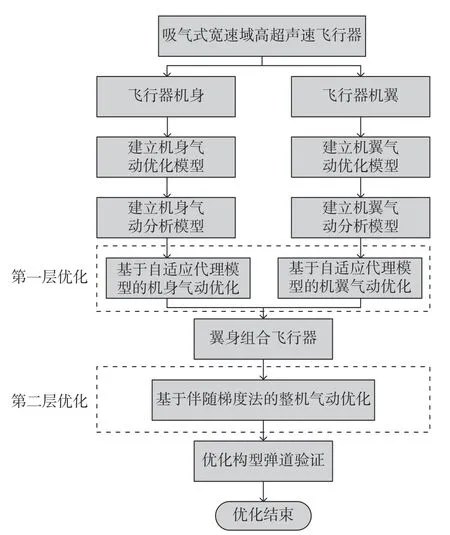
圖1 基于翼身分解的分層優化思路Fig.1 Multi-layer optimization idea based on wing body decomposition

1 飛行任務描述

本文研究的對象是水平起降的寬包線高超聲速飛行器，其動力系統采用RBCC 組合動力發動機。飛行器的典型飛行任務剖面如圖2 所示。整個任務的飛行速域范圍Ma=0～8，高度范圍H=0～50 km。

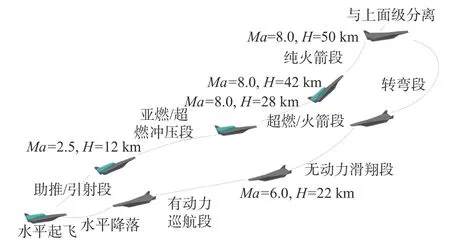
圖2 飛行任務剖面Fig.2 Flight mission profile

2 優化問題描述

2.1 問題提出

2.1.1 機身優化目標

本文采用加權求和法對優化結果進行評估。將阻力系數作為本文的優化目標，即：

其中，X為飛行器的外形優化設計變量，J為優化問題的目標函數。

對一定量的評估點的目標函數按式（2）進行標準化處理，Ji為第i個評估點的目標函數值，為樣本中的目標近似最小值，為近似最大值：

最后得到的優化目標函數為：

其中：Jbody為 總的優化目標函數，N為優化評估點數目，ωi為 權重因子，為每個評估點標準化處理后的目標函數值。

將馬赫數1.2、2.5、5.5、8.0 作為氣動優化評估點。權重系數選取以基準彈道為參考，各評估點的權重系數為燃料消耗對阻力系數的偏導數。考慮到實際彈道的結果數據往往以離散的形式給出，各評估點的權重系數可表示為：

其中，ωi為權重因子；mF為燃料質量；CDb為阻力系數；ΔmF,i為第i個評估點下飛行器燃料消耗，是阻力系數的函數。通過式（4）可以看出如果在某個優化評估點阻力系數變化對燃料質量變化的影響越大，則這個計算點在多目標向單目標轉化中所獲得的權重也越大。最終獲得的權重系數如表1 所示。

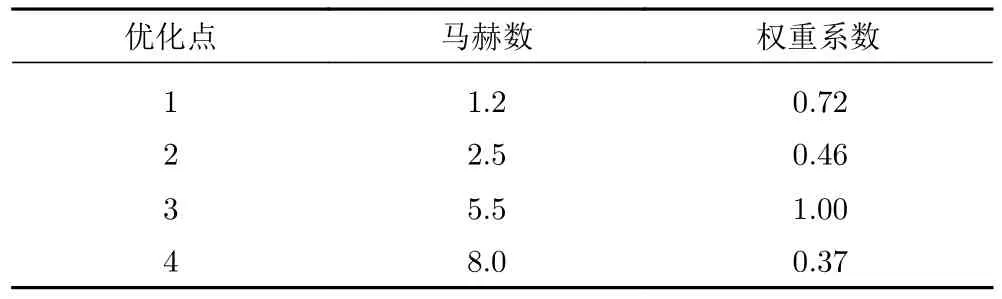
表1 機身優化評估點權重系數Table 1 Weight coefficients of the airframe optimization evaluation points

2.1.2 機翼優化目標

機翼優化設計同樣需要采用多點優化方法，式（5）為其優化目標。但與機身不同的是，機翼需要承擔飛行器起飛時絕大部分的升力，因此需要將計算起飛時Ma=0.4 的點作為優化分析點：

其中Jwing為機翼的優化目標函數。

參考基準彈道，最終得到機翼優化的評估點與權重如表2 所示。

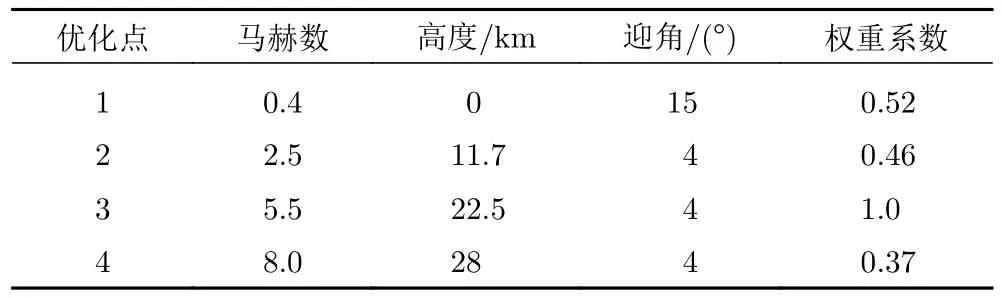
表2 機翼優化評估點計算狀態與權重Table 2 Computational conditions and weights for the wing optimization evaluation points

2.2 優化約束

表3 為機身優化問題的主要約束變量和范圍。變量范圍均根據工程估算給出；其中為焦點相對位置，假定飛行器機身的質心相對位置為0.6。機翼優化問題的約束變量和范圍如表4 所示。

表3 機身約束變量及約束范圍Table 3 Airframe constraint variables and ranges

表4 機翼約束變量及約束范圍Table 4 Wing constraint variables and ranges

3 飛行器氣動分析建模

3.1 物理模型

飛行器基準構型采用翼身組合體的氣動布局形式（圖3），全長約32 m，最大翼展約19 m，進氣面積10 m2，起飛質量約130 t。

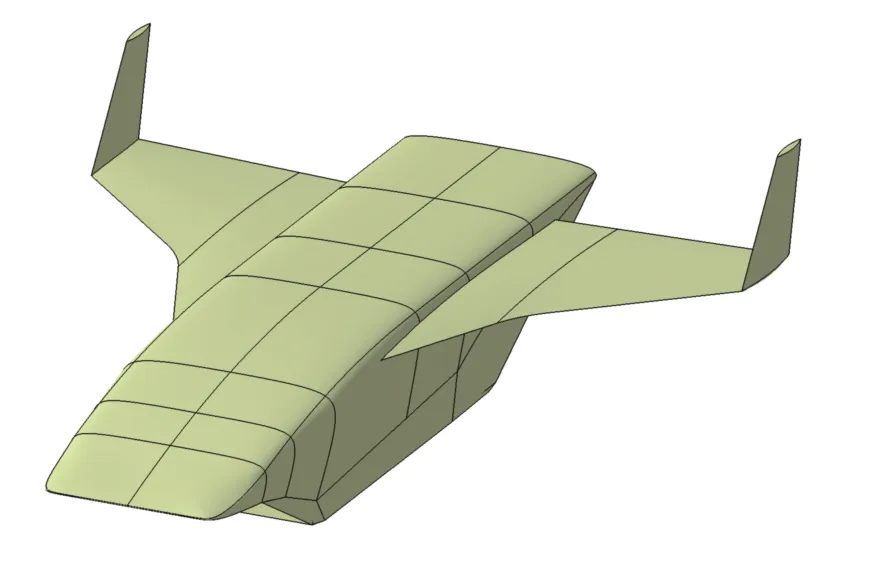
圖3 吸氣式高超聲速飛行器基準外形Fig.3 Basic shape of the air-breathing hypersonic vehicle

機身參數化建模采用模線設計法，即通過構造飛行器不同位置的幾個截面形狀和每個截面的輪廓曲線來描述飛行器外形。如圖4 沿飛行器縱軸設置5 個截面并對截面上的輪廓曲線進行參數化建模（圖5），在二次曲線上選擇一個控制點，則每個截面只用hi和 θi兩個變量就能表示。其中：ai為z=0 對稱面機身上表面輪廓線到下表面的距離；w為發動機寬度Wengine的一半；hi和 θi分別為各截面控制點的y坐標、輪廓的底部切線與x軸的夾角參數化；下標i為截面編號，取1～5 的整數。

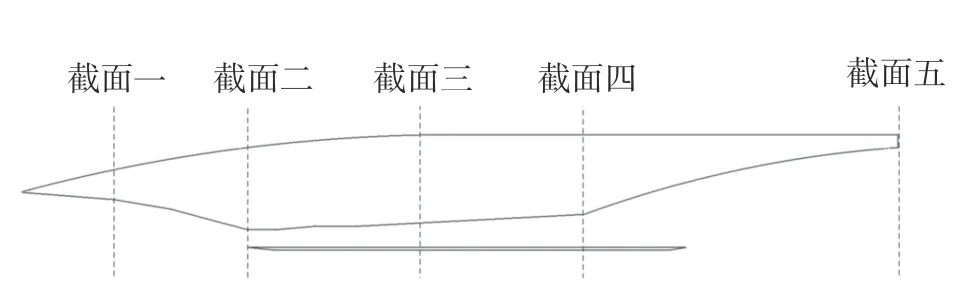
圖4 z=0 面上飛行器縱向輪廓及截面位置Fig.4 Longitudinal profile of the vehicle at z=0 and the cross-section positions

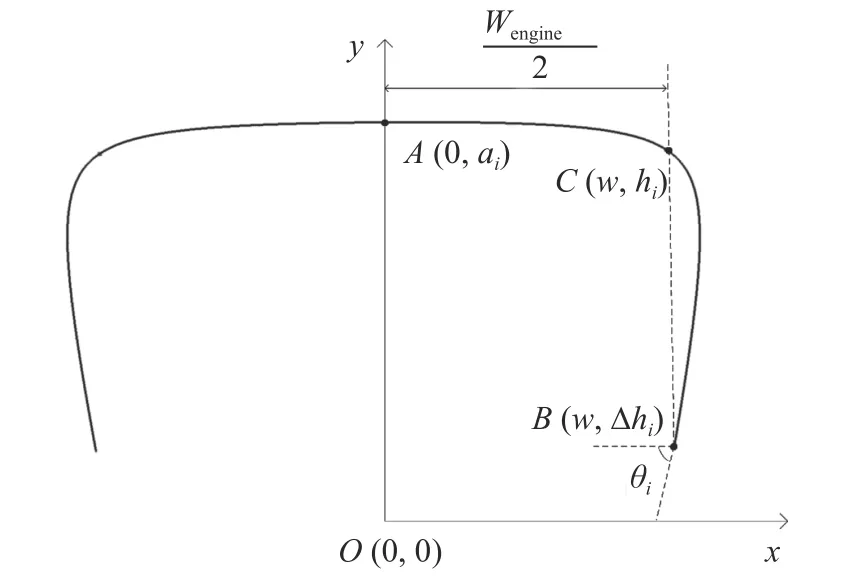
圖5 飛行器機身截面輪廓和參數Fig.5 Cross-section profile and parameters of the vehicle fuselage

飛行器頭部通過冪函數進行參數化設計，從y軸正方向向下俯視的輪廓曲線表達式為：

將n作為參數化變量，頭部形狀參數化示意圖如圖6 所示。最終完成的機身參數化模型三視圖如圖7所示。將發動機寬度作為參數化變量，進氣高度可經計算得到。對于尾噴管，在入口高度一定的情況下，其長度是影響其氣動特性的主要參數[15]，故取尾噴管長度作為設計變量。機身設計變量與范圍如表5所示。

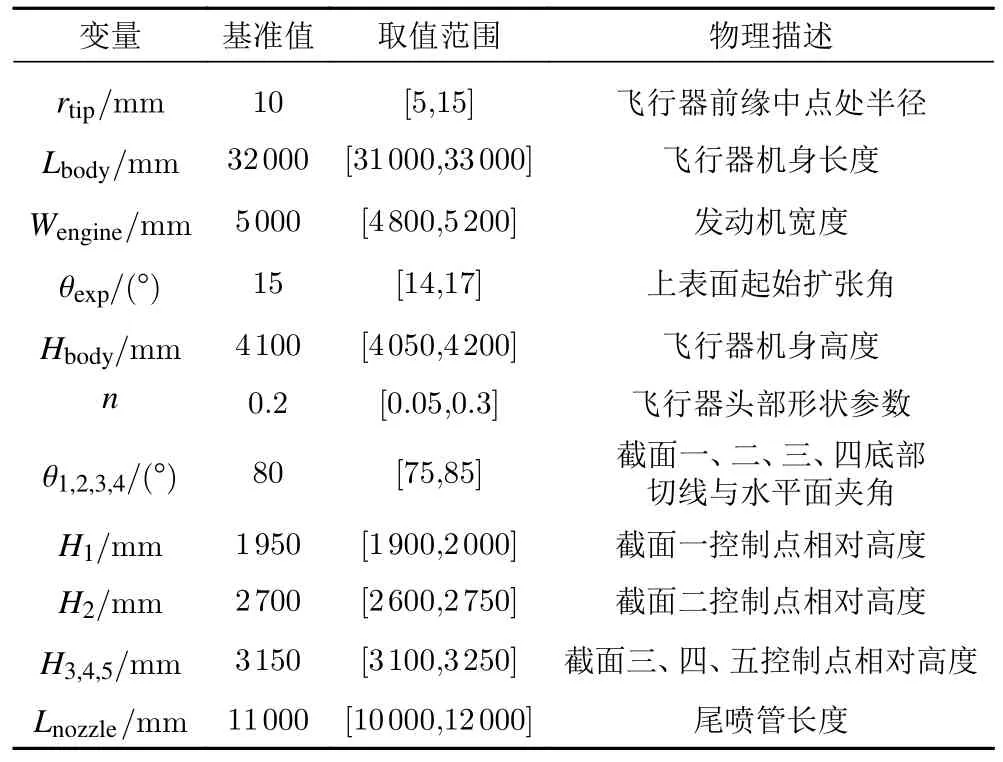
表5 機身設計變量與范圍Table 5 Body design variables and ranges

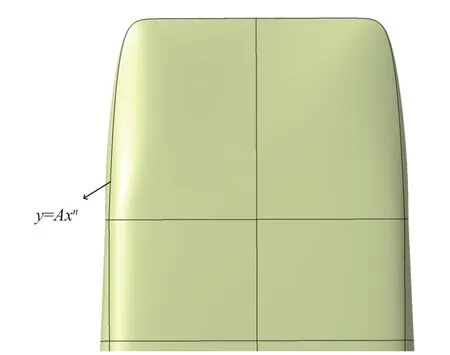
圖6 頭部形狀參數化示意圖Fig.6 Schematic diagram of the parametric vehicle head

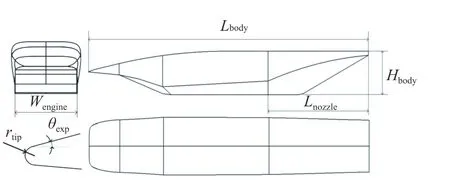
圖7 機身參數化模型三視圖Fig.7 Three views of the parametric fuselage model

水平機翼與垂尾組成的機翼建模如圖8 所示。機翼的設計變量與范圍如表6 所示。

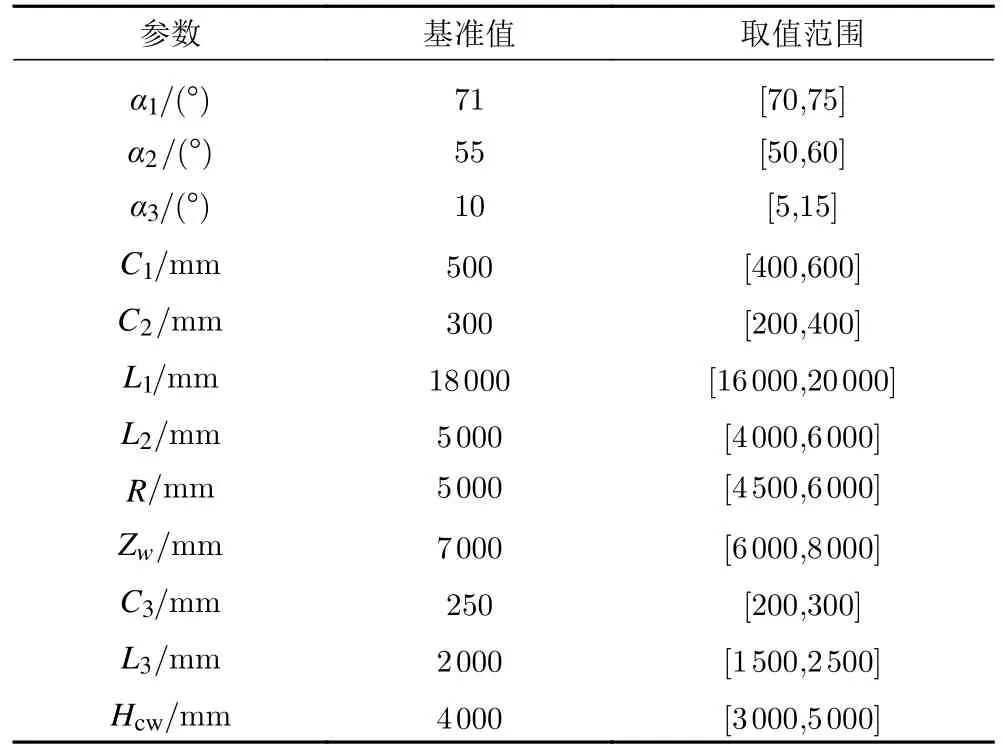
表6 機翼設計變量與范圍Table 6 Wing design variables and ranges

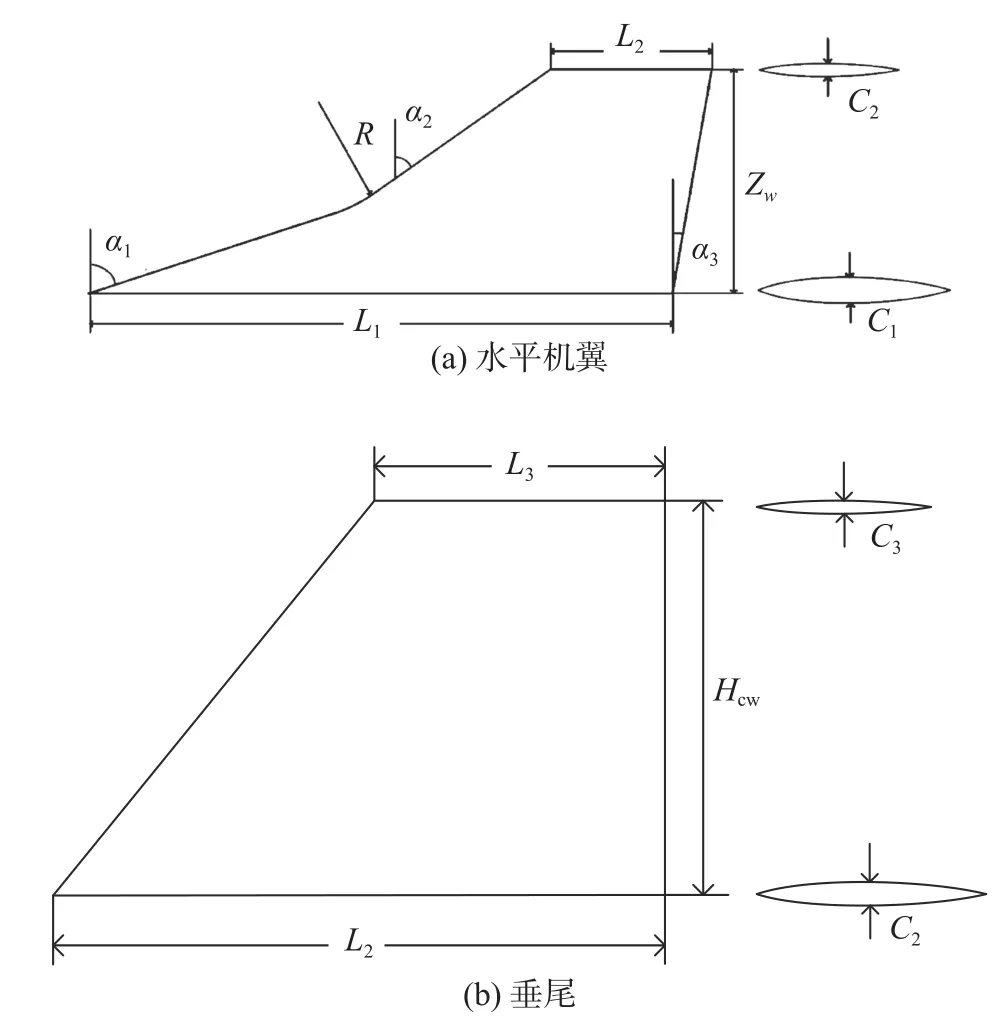
圖8 機翼參數化建模Fig.8 Parametric modeling of the wings

3.2 氣動特性計算模型

本文按照算力界面將整個流場劃分為發動機內、外流場兩部分，該劃分方式對于絕大多數吸氣式高超聲速飛行器在寬包線范圍內的研究有較好的適用性[16]。發動機內流場包括隔離段與燃燒室，采用準一維流計算，其他所有區域都定義為外流場，采用CFD 計算。本文的氣動/推進算力界面劃分如圖9 所示，ABCD四點范圍內劃為推進學科，其余部分劃為氣動學科。

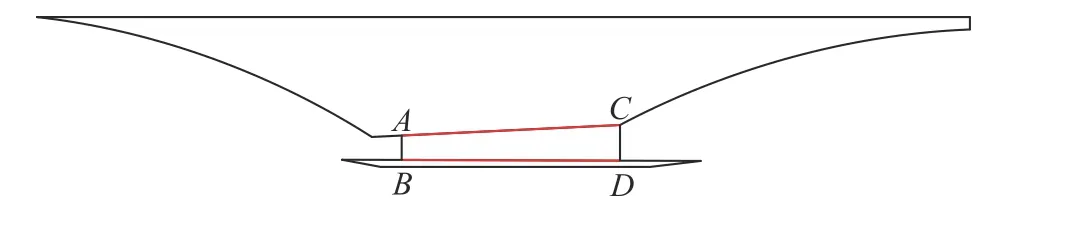
圖9 氣動/推進算力界面劃分Fig.9 Aerodynamic/propulsion calculation interface division

4 基于分層優化的氣動優化框架

基于提出的氣動優化問題，本文構建面向具體問題的氣動優化框架。為了保證優化精度和提高優化效率，本文在優化框架中設計了兩層優化，如圖10所示。

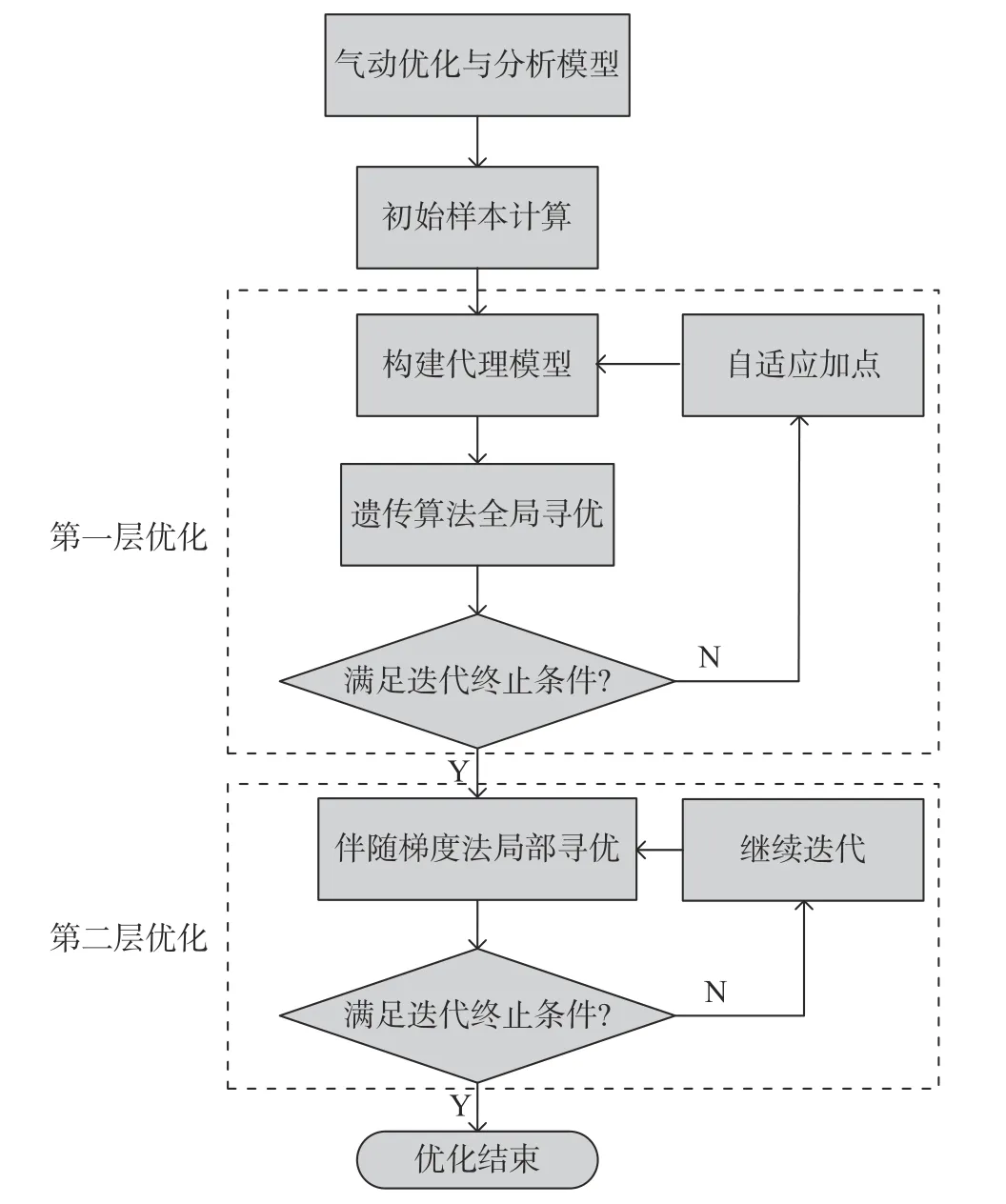
圖10 氣動優化框架流程圖Fig.10 Flow chart of the aerodynamic optimization framework

第一層優化通過代理模型在全局范圍內進行尋優，求解優化加點準則[17-18]定義的子優化問題，引入自適應加點提升全局搜索效率，本層的優化對象為單獨的機身與機翼。當基于自適應代理模型的優化迭代一定次數后，繼續加點對最優值附近的代理模型精度提升有限，此時可以在第一層優化的基礎上進行第二層優化。第二層優化為局部優化，優化算法為最速下降法[19]，梯度信息可通過離散伴隨法獲得，該層的優化對象是翼身組合飛行器。

4.1 基于自適應Kriging 代理模型的第一層優化

4.1.1 自適應Kriging 代理模型的加點策略及改進

為了提高優化效率減少計算量，將Kriging 代理模型引入本文的優化問題[20-21]。基于代理模型直接優化仍然需要計算大量的樣本，且盲目地在全局范圍內加點會造成計算資源的浪費。為了提高優化效率，需采用一種快速高效的加點策略來研究本文的優化問題。Kriging 代理模型的加點準則有極值加點準則、EI 加點準則、誤差最大加點準則等[22]，但每輪迭代只能加入一個新的樣本點，導致優化效率較低，而并行加點法能在一輪內同時加入多個樣本點，在計算資源充足的情況下，比單一加點法的優化效率更高，能極大地縮短優化所需的時間。

在所有的并行加點準則中，基于EI 準則的自適應加點手段應用最為廣泛，但由于EI 準則存在固有缺陷，在全局最優值附近往往無法精確收斂。針對這個問題，本文提出的改進方法是將代理模型的預測最優值作為每步迭代的新增樣本之一來改善搜索的局部收斂性。該方法本質上是極值加點準則與基于EI 準則的并行加點法的結合，在尋優前期EI 準則可以發揮其全局性，克服極值加點準則容易陷入局部收斂的缺陷；尋優后期全局最優解的范圍大致確定，極值加點準則可以起到加速收斂的作用。

4.1.2 算例測試

為了檢驗離散伴隨方法流程的有效性，應對其進行算例測試。本文采用翼型NACA0012 算例作為實際工程問題。該算例的來流狀態為：總溫T=311 K，總壓p=101325 Pa，馬赫數Ma=0.7，迎角α=1.55°。為了便于控制翼型形狀，需要對其進行參數化處理，這里采用的參數化方法為CST 方法[23]。對NACA 圓頭尖尾系列的翼型，規定翼型弦長為1 m，則CST 曲線的數學表達式為：

其中：ai為控制參數，n為Bernstein 多項式次數，=n!/[i!(n-i)!]，ΔyTE為翼型后緣厚度。算例采用6階Bernstein 多項式，翼型上下表面的形狀均由7 個參數控制，設計變量共14 個，其區間設置可參考文獻[24]。

本文在保證升力不下降的同時對翼型進行減阻設計，從而進一步提高翼型在設計點的性能。該優化問題可表述為：

其中：CDa為翼型的阻力系數，CLa為優化后翼型的升力系數，CLa1為優化前翼型的升力系數。

采用序列二次規劃法（NLPQL）作為該算例的優化算法，其他優化條件保持不變。為了驗證本文離散伴隨法的計算精度，利用有限差分法與離散伴隨方法分別求解初始翼型阻力系數對外形參數的梯度并將計算結果進行對比，兩種方法的擾動步長均設為0.001。表7 給出了兩種方法的梯度計算結果，由表可知14 個外形參數的最大差別僅為3.34%，因此可認為伴隨梯度方法的計算結果可靠，可用于之后的氣動優化。

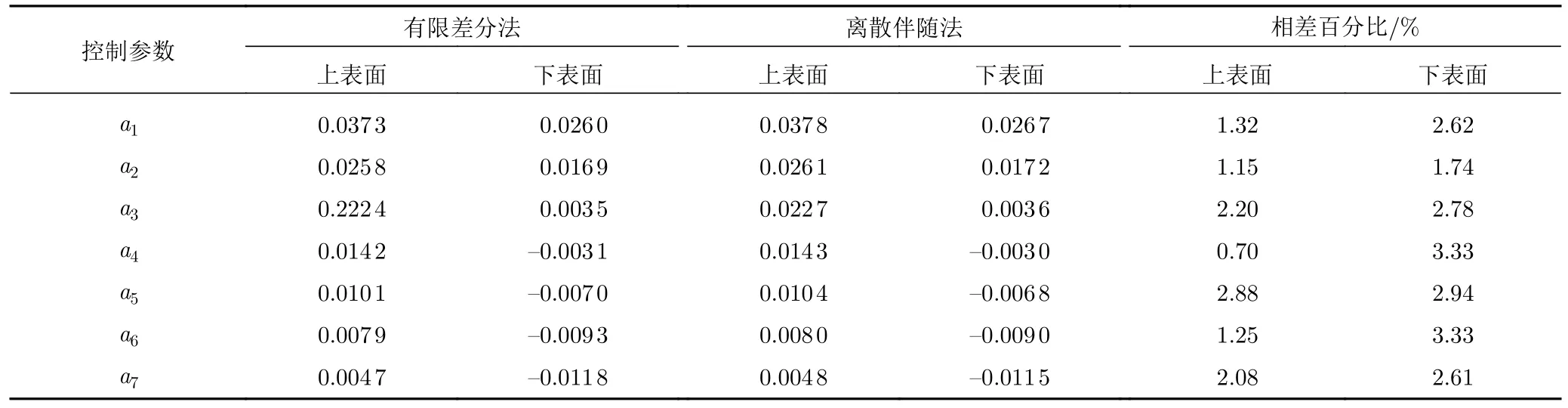
表7 兩種方法的梯度計算結果對比Table 7 Comparison of the gradient calculation results between the two methods

下面通過算例來測試改進方法的有效性。本文主要考慮三種并行加點方法：混合加點法、Kriging 信任法、多點EI 法，其中混合加點法是在每步迭代時分別基于4.1.1 節中所提到的三種單一加點準則進行加點；Kriging 信任法為基于EI 準則的經典并行加點法，詳見文獻[25]；多點EI 法由文獻[26]提出，是一種較為高效的并行加點方法。對于以下算例，所有并行加點法每次迭代均增加3 個新樣本點，改進的加點策略每步迭代基于原方法添加2 個新樣本，基于極值加點準則添加1 個新樣本。初始樣本的訓練方法均為拉丁超立方抽樣，基于代理模型的全局尋優方法均采用遺傳算法。

G9 函數是測試全局優化算法的經典算例[27]，共有7 個設計變量和4 個約束，由于其優化可行域小、收斂下降量級大，優化難度較高，可對本文的尋優策略進行很好的檢驗。

G9 函數的數學模型為：

其中xi∈[-10,10]，i=1,···,7。通過樣本訓練得到300 個點作為初始樣本建立Kriging 代理模型，采用多種加點策略來提高代理模型的近似精度。各自適應加點策略的收斂流程如圖11 所示，優化結果與調用函數模型的次數如表8 所示。

圖11 G9 算例各種自適應加點策略的收斂流程Fig.11 Convergence process of various adaptive point addition strategies for the G9 case

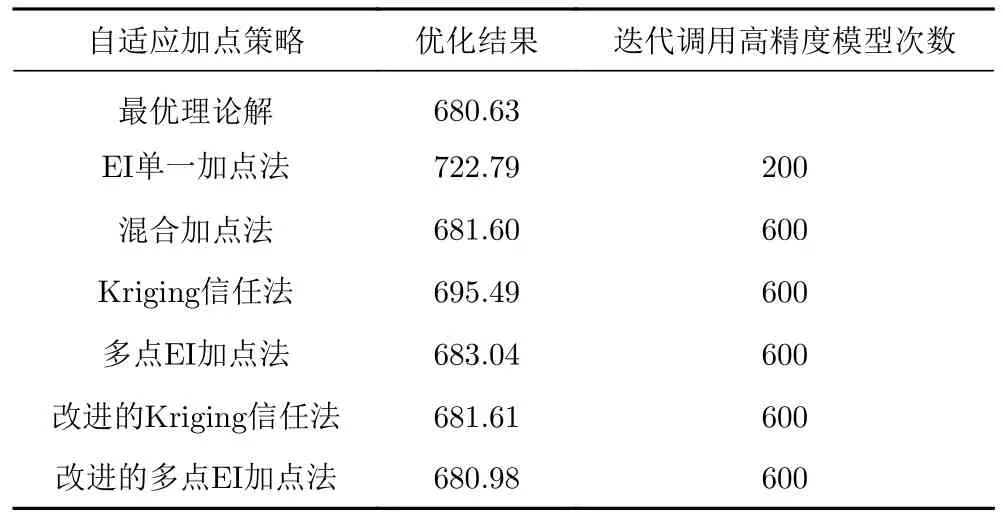
表8 G9 函數優化結果及調用高精度模型次數對比Table 8 Comparison of the G9 function optimization results and the times of calling high-precision models

根據不同并行加點策略之間的對比，可以發現對于復雜函數，在調用同樣次數高精度模型的條件下，改進后的兩種方法相比于改進前在收斂速度和結果精度上都有了較大的提高，說明本文提出的改進措施是有效的。多點EI 加點法改進后的優化效率提升更大，是本文研究的幾種并行加點法中最優的加點策略，因此本文采用改進后的多點EI 法來解決之前提出的優化問題。

4.2 基于離散伴隨法的第二層優化

為了在第一層優化的基礎上獲得整體氣動性能更優的方案，需進一步采用梯度算法局部尋優。本文將離散伴隨方法引入優化過程以降低求解梯度時的氣動計算量，建立了基于伴隨梯度法的氣動優化流程如圖12 所示[28]。

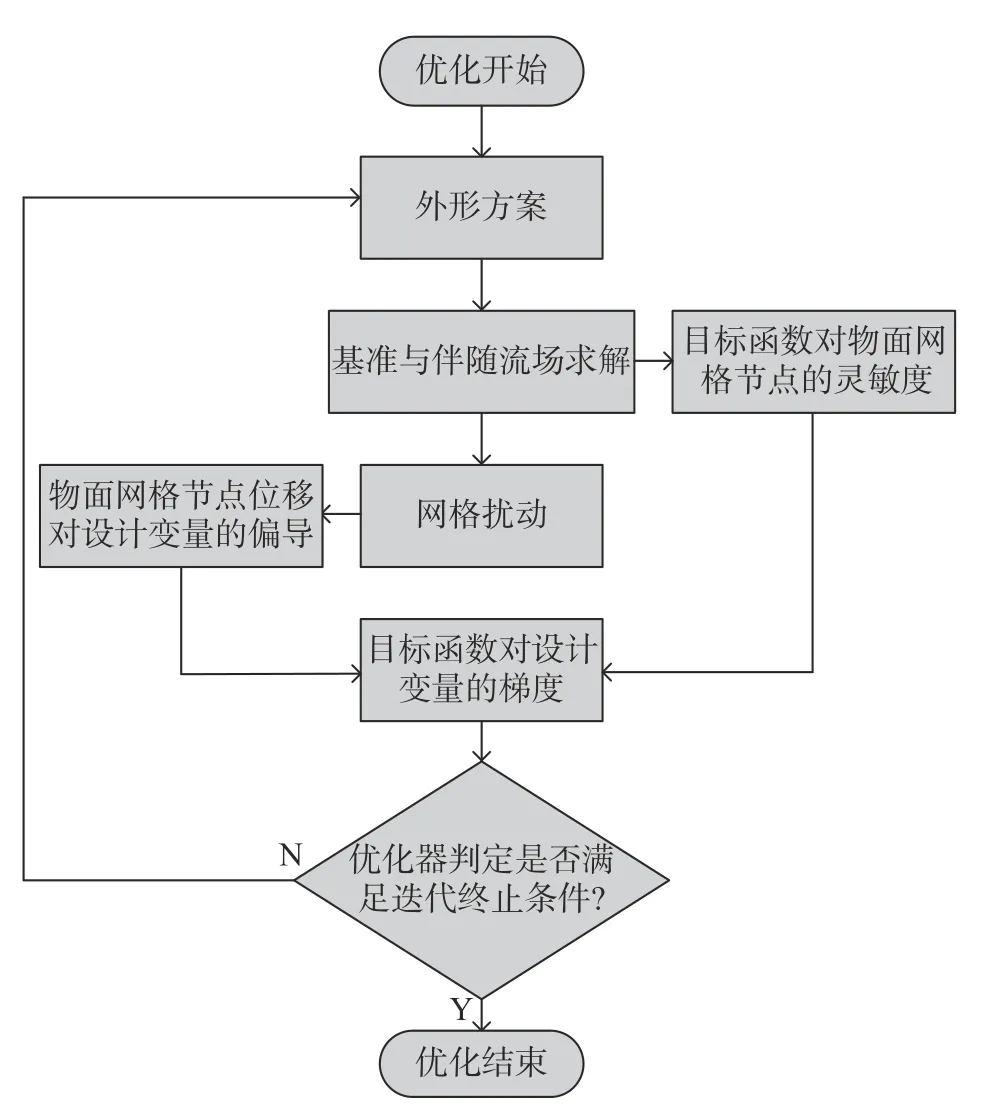
圖12 基于離散伴隨方法的優化流程圖Fig.12 Flow chart of the optimization process based on the discrete adjoint method

5 優化結果

5.1 第一層優化結果

表9 給出了機身外形優化結果，該外形與基準外形的對比如圖13 所示。圖14 和圖15 分別給出了馬赫數5.5 時基準外形與優化外形在對稱面處的靜壓與馬赫數云圖。由以上結果可知相比于基準外形，考慮所有約束的機身優化外形整體尺寸略有縮小、減阻效果顯著，而且靜穩定性、容積率、發動機進氣條件三項指標也均有了明顯的提升。

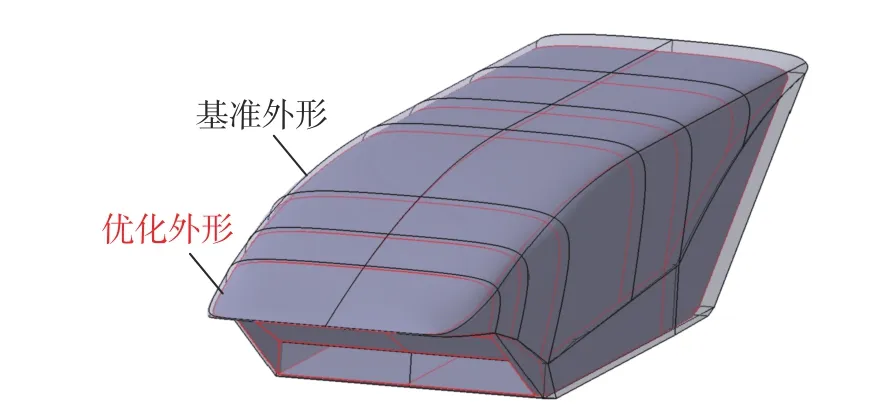
圖13 機身優化外形與基準外形對比Fig.13 Comparison between the optimized and reference fuselage shapes

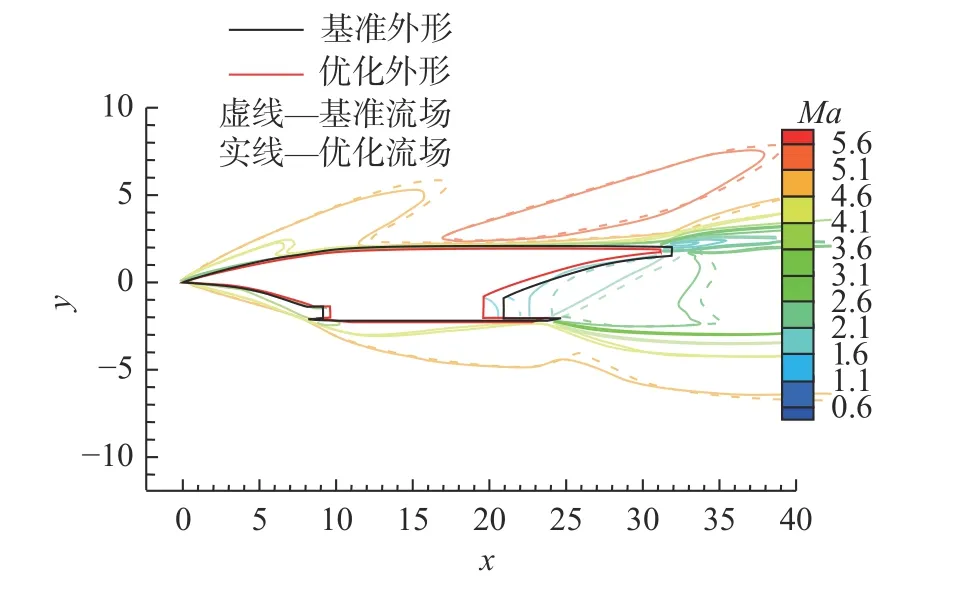
圖15 Ma=5.5 時機身對稱面處的馬赫數對比Fig.15 Comparison of Mach number in the symmetry plane of the fuselage at Ma=5.5

表9 機身第一層優化結果Table 9 First layer optimization results of the fuselage

機翼最終的優化結果如表10 所示，該外形與基準構型的對比如圖16 所示，可以看出優化外形的水平機翼面積縮小，垂尾弦長增加但高度減小。圖17和圖18 分別給出了馬赫數5.5 時機翼基準外形與優化外形在下表面的靜壓云圖和對稱面的馬赫數云圖。馬赫數5.5 時機翼半展長處的壓強如圖19 所示，可以看出優化后機翼前緣壓強顯著降低，減阻效果明顯。

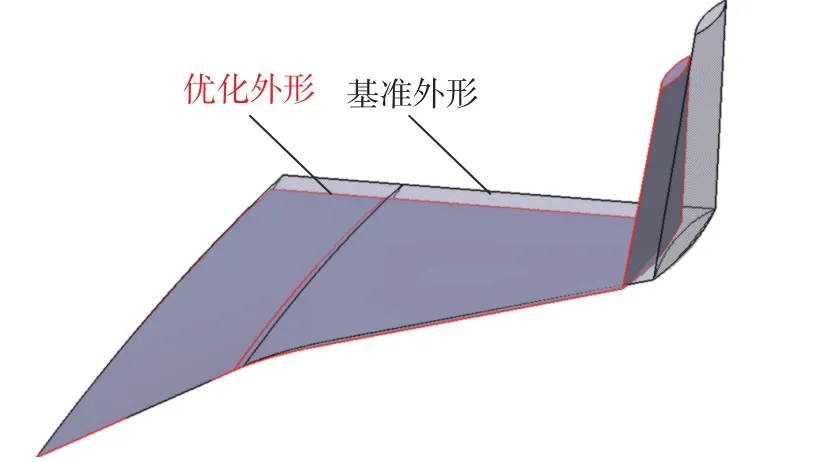
圖16 機翼基準外形與優化外形對比Fig.16 Comparison between the baseline and the optimized shape of the wing

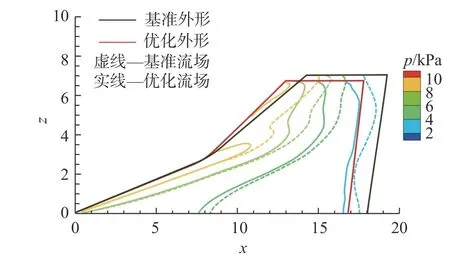
圖17 Ma=5.5 時機翼下表面的靜壓對比Fig.17 Comparison of static pressure on the lower surface of the wing at Ma=5.5

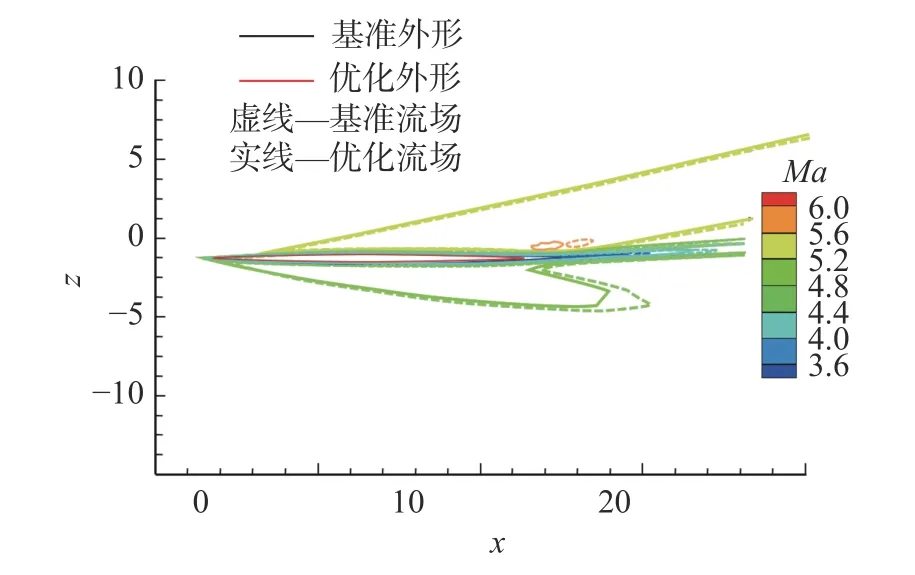
圖18 Ma=5.5 時機翼對稱面處的馬赫數對比Fig.18 Comparison of Mach number in the symmetry plane of the wing at Ma=5.5

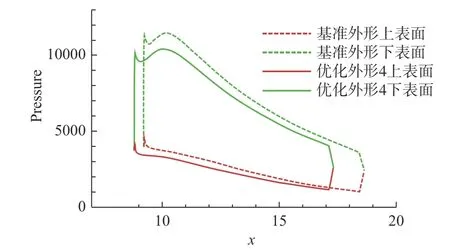
圖19 Ma =5.5 時機翼半展長處上下表面壓強對比Fig.19 Comparison of pressure on the upper and lower surfaces of the wing at half-wingspan for Ma=5.5

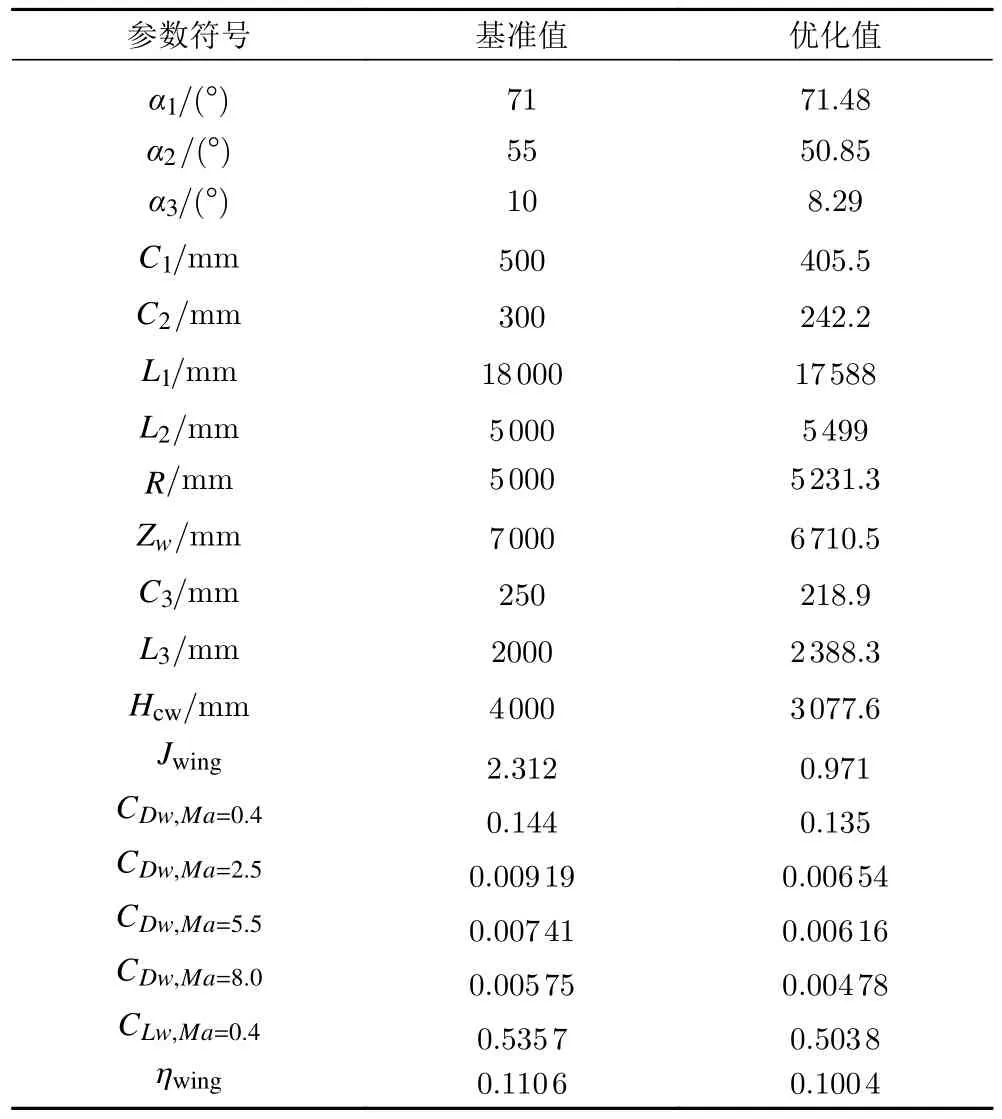
表10 機翼外形優化結果Table 10 Wing shape optimization results

5.2 第二層優化結果

該層優化的目標函數與機身、機翼的優化目標形式相同，記為Jcom。優化評估點和權重選擇表1 中的4 個典型特征點及其相應權重，優化約束為機身、機翼優化問題的約束集合。翼身組合體的設計變量包括了機身、機翼優化問題的設計變量以及描述翼身相對位置的兩個新變量，共24 個外形參數。新增的兩個外形參數的詳細描述如圖20 所示。翼身組合體優化前后的各項參數如表11 所示，優化前后的外形對比如圖21 所示，可以看到兩者外形較為近似，伴隨優化外形的整體尺寸略有縮小，4 個氣動評估點的阻力系數均有所降低，目標函數比優化前減小了19.6%。圖22 和圖23 分別給出了馬赫數5.5 時第一層優化結果與伴隨優化外形在對稱面處的靜壓與馬赫數云圖，從圖中可以看出相比于第一層優化的外形，伴隨優化外形的前緣高壓區面積略微減小，后緣高壓區面積略有增大，在滿足約束的前提下使阻力進一步降低。

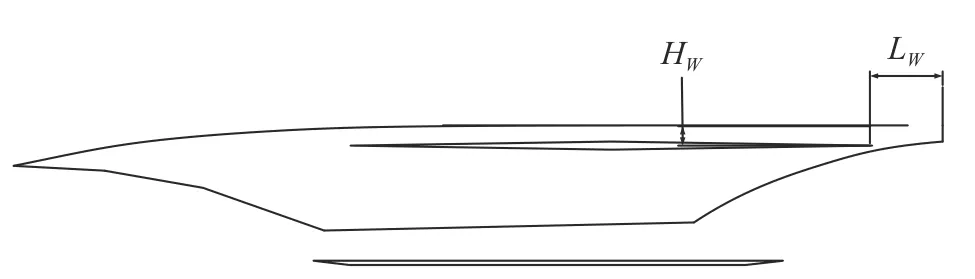
圖20 新增兩個設計變量的圖形描述Fig.20 Schematic description of the two new design variables

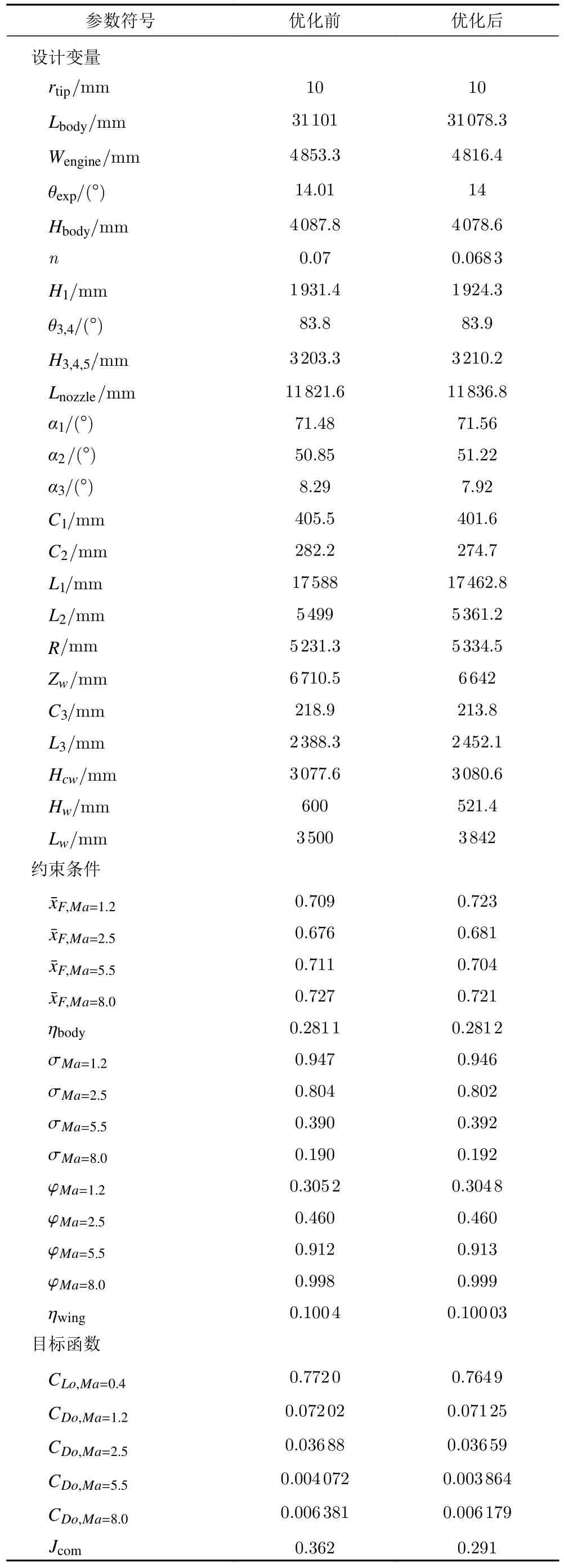
表11 翼身組合體優化前后參數對比Table 11 Comparison of parameters before and after optimization of the wing body assembly

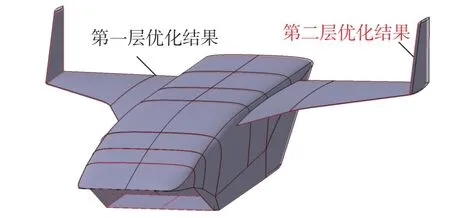
圖21 第二層優化后的飛行器外形Fig.21 Vehicle shape after the second layer optimization

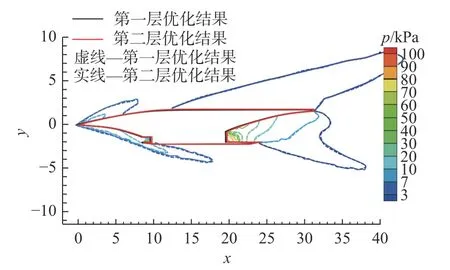
圖22 Ma =5.5 時兩層優化結果在對稱面處的靜壓對比Fig.22 Comparison of static pressure in the symmetry plane for two-layer optimization at Ma =5.5

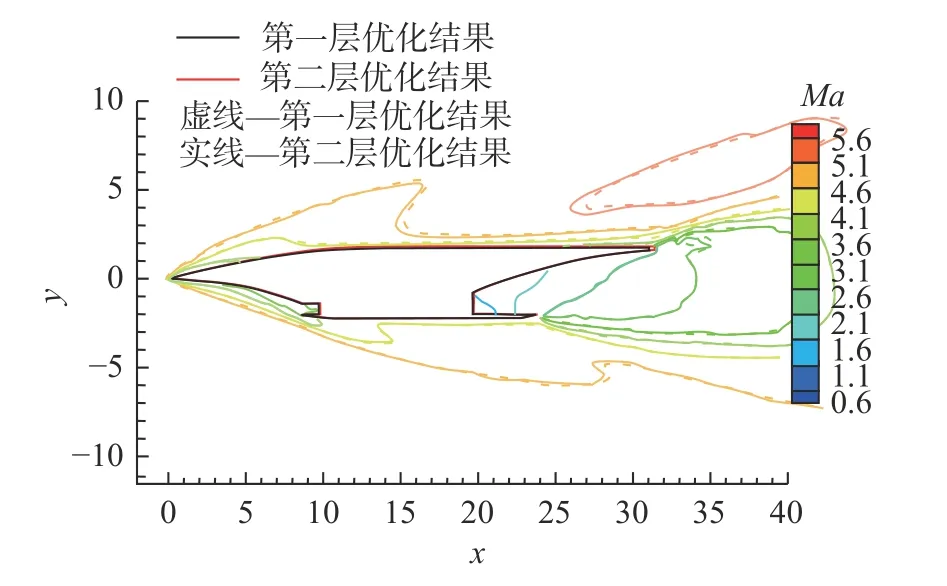
圖23 Ma=5.5 時兩層優化結果在對稱面處的馬赫數對比Fig.23 Comparison of Mach number in the symmetry plane for two-layer optimization at Ma =5.5

6 結論

本文以兩級入軌飛行器中的下面級—吸氣式高超聲速運載器為研究對象，基于翼身分解的思路構建了多評估點的氣動優化模型；建立了飛行器的氣動分析模型，對算力界面進行劃分并使用“CFD+準一維流”的氣動求解流程；提出了基于分層優化的氣動優化方法并對改進的自適應Kriging 代理模型加點策略進行算例測試，證明了改進措施的有效性；最后通過搭建的優化框架對吸氣式高超聲速飛行器的氣動外形進行了分層優化。

1）針對本文算例模型，驗證了根據燃料消耗對阻力系數的偏導數給出多優化評估點的權重系數的方法是可行的；

2）將代理模型的預測最優值作為每步迭代的新增樣本之一的Kriging 代理模型的加點準則可以改善搜索的局部收斂性；

3）本文提出的優化方法在滿足各學科約束的條件下可以使飛行器在4 個優化評估點處的阻力系數均有所減小。