面向飛行試驗的多源氣動數據智能融合方法

王 旭，寧晨伽，王文正，張偉偉，*

(1.西北工業大學 航空學院，西安 710072；2.電子科技大學 航空航天學院，成都 611731)

0 引言

作為當前世界航空航天強國爭相追逐的重點研究方向，高超聲速飛行器具有高速度、強機動、超遠程、強突防等優勢[1]，這些特點對飛行器氣動性能評估提出了更高的要求。如何實現高超聲速氣動性能的精確評估與預測是當前高超聲速領域高性能飛行器發展的關鍵難題[2-3]。

長期以來，計算流體力學方法、風洞試驗方法和飛行試驗都被作為航空航天領域氣動性能評估的三大手段。由于在物理模型精度、試驗成本與測量能力等方面互有優劣，這些手段在飛行器設計中發揮著不同的作用，同時獲取的氣動數據需要相互驗證。在亞聲速與跨聲速階段，風洞試驗可以直接模擬飛行條件下的真實飛行環境，然而隨著流動進入高超聲速范圍，天地數據不一致性問題開始凸顯[4]。

高超聲速氣動數據天地差異性的原因主要體現在試驗與數值手段難以直接精確模擬飛行條件，量熱完全氣體效應的差異和黏性干擾現象的出現對氣動數據的一致性產生重要影響。在高超聲速氣動問題中，流動具有明顯的熱效應，并且工作環境的氣體比較稀薄，雷諾數較小。在高馬赫數、低雷諾數、高焓值的條件下，高超聲速流動呈現出較強的復雜性，其復雜流動現象包括薄激波層、熵層、真實氣體效應、黏性干擾、稀薄氣體效應等等[5-6]。由于常規高超聲速風洞試驗馬赫數范圍有限，并且難以通過控制氣體密度來達到低雷諾數的要求，不能充分模擬真實飛行過程中的黏性干擾效應與真實氣體效應，導致風洞試驗數據與真實飛行試驗下氣動數據差異較大[7]。

為了提升天地氣動數據一致性，數據融合方法逐漸開始[8-9]被應用于多源氣動數據的預測模型構建。所謂數據融合方法，是指根據多種信息來源（同質或異質），根據某標準在空間或時間上進行組合，獲得被測對象的一致性描述，并使得該信息系統具有更好的性能。近些年來，此類方法被廣泛應用于數值仿真與風洞試驗數據的融合建模中。Meysam 等[10]針對返回艙外形的飛行器開展了數值仿真數據與風洞試驗數據的融合建模方法研究。結果顯示，對于高超聲速氣動數據庫構建問題，所采用的Co-Kriging 類數據融合模型[11-12]可以有效提升氣動數據庫建立效率，在相似外形下氣動數據利用效率可以提升80%以上。Ghoreyshi 等[13-14]利用風洞試驗數據和CFD 仿真結果融合構建了飛機的高維定常氣動模型，從而建立了定常氣動數據多源數據庫。利用這一方法使得數據庫構建所需的試驗樣本降低30%以上。基于以上研究，Yondo 等[15]綜述了氣動數據代理模型方法的發展以及抽樣方法對航空航天領域數據庫構建的影響，同時對數據融合模型的發展進行了展望。

針對高超聲速飛行器天地氣動數據差異，國內的研究團隊和學者也開展了豐富的研究。陳堅強等[2]綜述了國內外高超聲速飛行器氣動力數據天地換算技術方面的研究現狀及趨勢，并分析了天地氣動數據關聯的兩大途徑：一是利用天地氣動數據差異，構建關聯修正模型，以此實現地面風洞試驗數據的修正與外推，從而提升天地一致性。在這一思路下，李金晟等[16]提出了一種適用于工程數據的天地氣動數據修正框架，在飛行辨識數據中取得了較好的修正結果；龔安龍等[17]結合關聯參數進行修正和改進，給出了高超聲速黏性干擾下的關聯修正結果；王文正等[18]提出了基于數學模型的氣動力數據融合準則和方法，以氣動力數據滿足的準則為依據，將不同類型的數據進行融合；鄧晨等[11]分別采用基于高斯回歸方法和梯度信息的數據融合模型對飛行試驗數據與風洞試驗數據進行融合，并對比了不同融合結果中飛行試驗氣動數據的精度提升。二是利用高超聲速氣動數據關聯參數，實現飛行狀態與地面試驗狀態的關聯參數對齊，從而提升天地一致性。在這一思路下，沙心國等[19]針對高超聲速氣動熱問題開展了關聯研究，并對比了不同關聯參數對關聯結果的影響。羅長童等[3,20]發展了基于自適應空間變換（adaptive space transformation,AST）的關聯參數數據挖掘方法，并將其應用于高超聲速氣動力關聯。

然而當前的天地氣動數據一致性研究大多還停留在實驗室階段，面向真實飛行環境的多源氣動融合依然存在未解決的問題。為了提升多源氣動數據庫的構建精度，獲取高效的飛行試驗氣動數據融合能力，在以上研究思路的基礎上，本文提出了一種面向飛行試驗氣動數據的天地氣動數據差異修正模型，以風洞試驗數據為低精度逼近量構建多源氣動數據融合的隨機森林模型。以某典型軸對稱飛行器為研究對象，本文開展了風洞-飛行試驗氣動關聯融合研究。針對不同飛行階段開展氣動數據交叉驗證的結果表明，所提出的隨機森林氣動數據融合框架可以有效提升氣動數據預測精度，在強噪聲、多物理量氣動數據干擾下依然具有很好的預測能力。相關工作為高超聲速多源氣動數據一致性提升提供了一種可行的解決方案。

1 風洞試驗與飛行試驗氣動數據

風洞試驗在中國空氣動力研究與發展中心完成，實現了目標對象飛行器在不同馬赫數、迎角和舵偏條件下的氣動力測試，相關結果的示意圖如圖1 所示。基于該風洞試驗結果，構建了復雜的氣動數據庫，用以完成不同飛行狀態氣動力的準確預測。

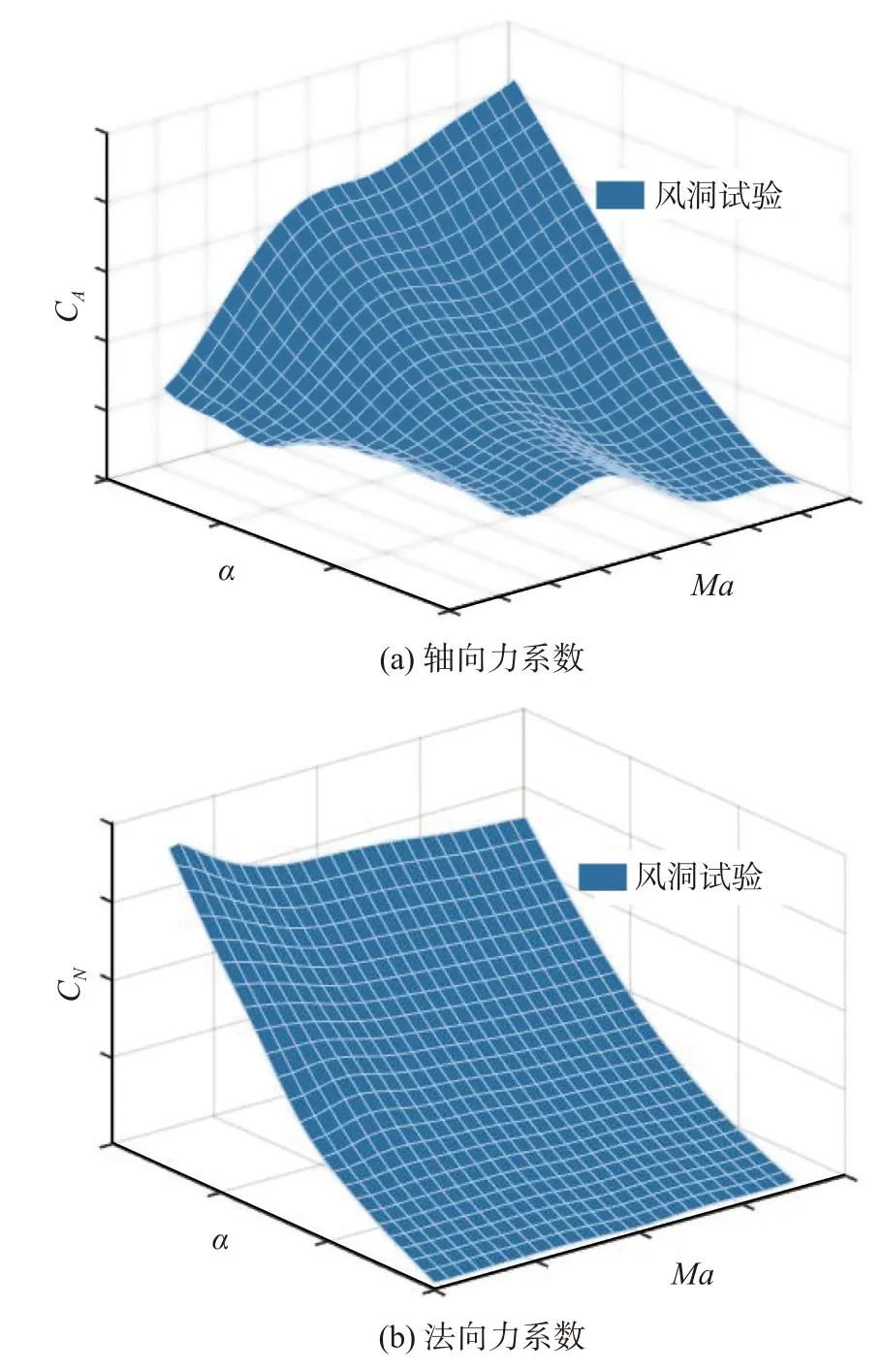
圖1 不同馬赫數和迎角下的風洞試驗結果Fig.1 Result of wind tunnel tests

以目標對象飛行器飛行試驗50～320 s 的氣動辨識數據為研究樣本進行數據融合建模。飛行器飛行馬赫數變化如圖2 所示，馬赫數在270 s 的飛行時間內產生了較大的變化，豐富的氣動特性為模型構建提供了充分的研究樣本。利用飛行器遙測數據開展氣動參數辨識，得到飛行器飛行狀態與氣動力響應歷程。其中，飛行器迎角α和側滑角β如圖3 所示，飛行器軸向力系數CA和法向力系數CN辨識結果如圖4 所示。

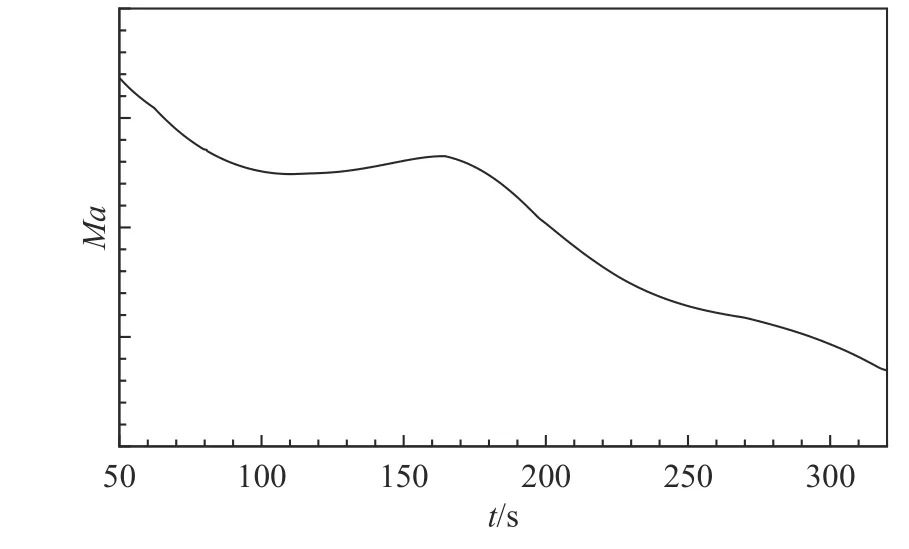
圖2 飛行過程馬赫數變化（50～320 s）Fig.2 Mach number variation during the flight (50～320 s)

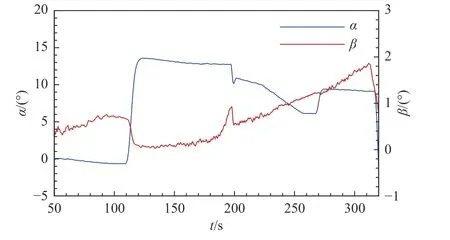
圖3 飛行過程迎角與側滑角變化（50～320 s）Fig.3 Variations of angle-of-attack and angle-of-sideslip during the flight (50～320 s)

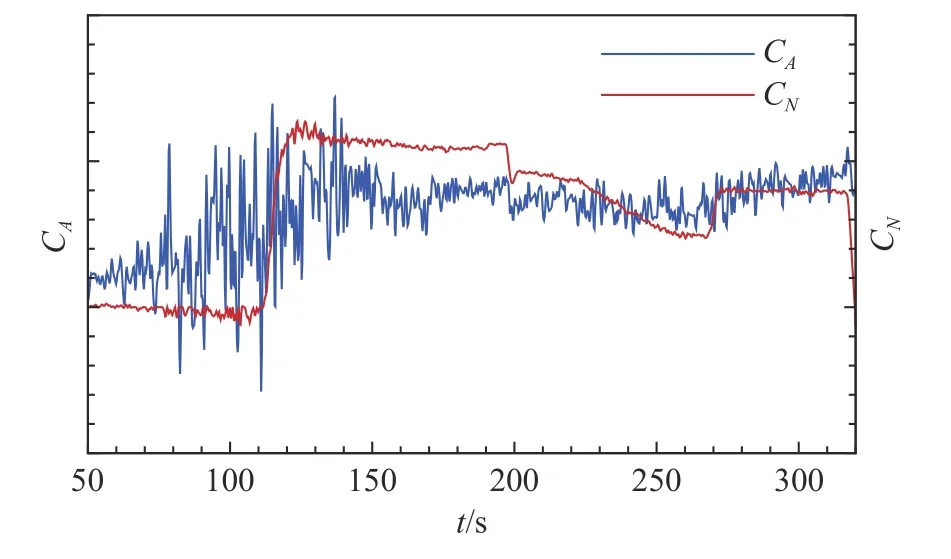
圖4 飛行參數辨識得到氣動力系數響應歷程（50～320 s）Fig.4 Time histories of aerodynamic coefficients during the flight (50～320 s)

由于風洞試驗不能完全匹配飛行條件，特別是雷諾數等關鍵物理量難以直接滿足。在氣動數據庫構建過程中，風洞試驗結果與飛行辨識結果存在一定的差異，這一問題在高超聲速飛行器氣動領域較為常見。對于上述飛行試驗的過程，氣動力響應歷程存在較大的差異，相關結果的對比如圖5 和圖6 所示。

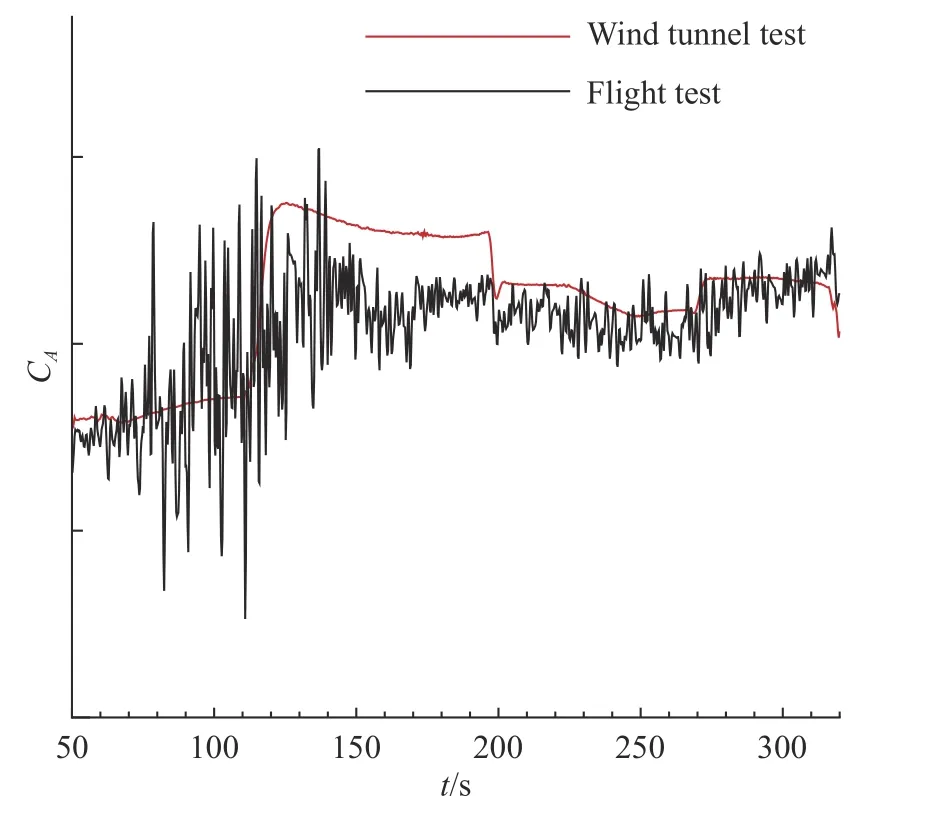
圖5 風洞試驗與飛行試驗軸向力系數對比Fig.5 Comparison of axial force between wind tunnel test and flight test

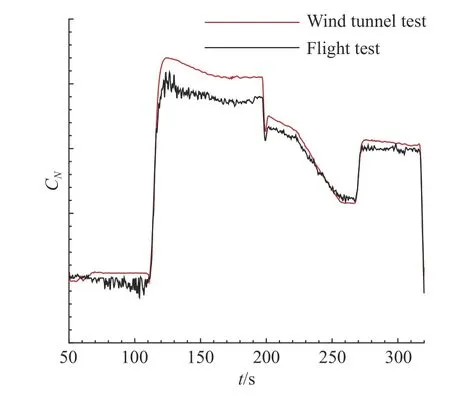
圖6 風洞試驗與飛行試驗法向力系數對比Fig.6 Comparison of vertical force between wind tunnel test and flight test

圖中黑色線代表飛行參數辨識得到的響應氣動力，由于傳感器靈敏度與精度的限制，相關結果存在一定的噪聲。而風洞試驗數據利用克里金插值實現，氣動力響應用紅色線表示。由于試驗條件、支撐干擾等差異的存在，天地氣動數據在數據庫中存在顯著差異，在工程中往往依賴于專家經驗和工程算法進行天地數據換算和修正工作。隨著數據挖掘、深度學習算法的發展，利用數據本身特性開展天地氣動數據融合正逐漸成為新的研究方向。

2 隨機森林數據融合框架

考慮到氣動數據的差異普遍存在于飛行過程，本文發展了一種基于隨機森林的飛行試驗天地氣動數據融合框架，用來提升風洞試驗數據與飛行試驗數據一致性，從而大幅提高飛行氣動數據預測精度。

2.1 隨機森林模型

考慮到飛行遙測數據存在較大噪聲，同時飛行過程氣動影響參數較為復雜，難以直接確定建模輸入。所以這里考慮構建隨機森林模型，以提升模型融合過程中處理復雜輸入數據的能力。相比于傳統神經網絡類回歸模型，隨機森林方法采用集成學習框架實現參數的學習和模型預測，可以充分利用多傳感器遙測數據、飛行姿態數據、地面風洞試驗數據來同時構建數據融合模型。

隨機森林（random forest,RF）是Breiman 等[21]提出的一種并行式集成機器學習方法。隨機森林通過集成大量決策樹達到較好的泛化性能，其通過Bootstrap 取樣法從D個訓練樣本中有放回地隨機選取n個樣本得到m個子集，并對每個子集單獨訓練一棵決策樹，將m棵決策樹預測結果的平均值作為回歸隨機森林的輸出。其建模流程如圖7 所示。

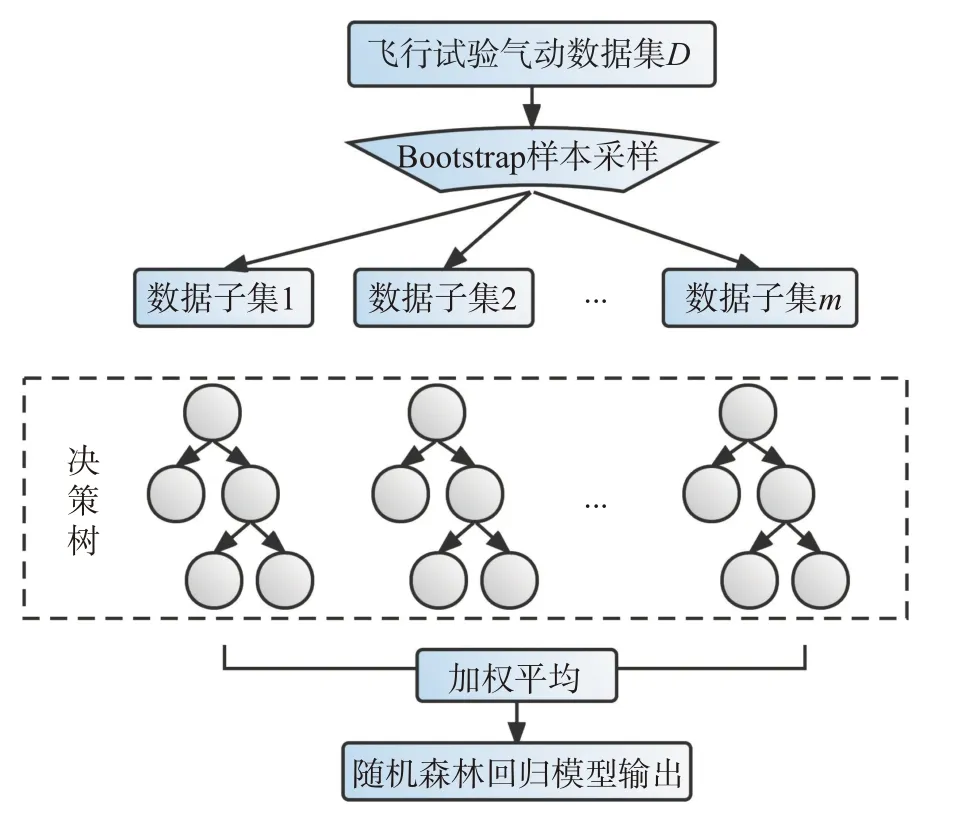
圖7 隨機森林氣動力回歸建模流程Fig.7 Process of regression modeling using random forest

2.2 面向飛行試驗的數據融合框架

本文結合數據融合方法與隨機森林模型，提出了一種可以結合不同輸入特征的隨機森林氣動融合架構。數據融合架構的構建流程如圖8 所示，這里采用循環隨機森林建模來調整模型輸入特征，避免森林結構的冗余。

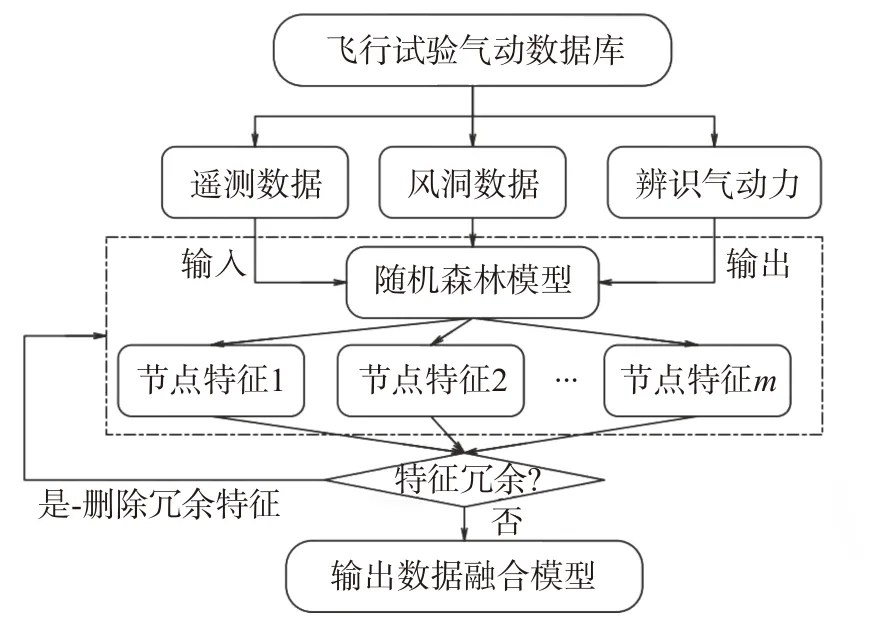
圖8 基于隨機森林的數據融合架構Fig.8 Aerodynamic fusion framework based on random forest

模型建模流程可以表述為：

第一步：基于飛行試驗氣動數據庫，利用遙測數據與辨識得到的氣動力系數，初步構建隨機森林模型，定義為隨機森林1。模型以9 個狀態量為輸入，表示為：a、Ma、ρ、α、β、d1、d2、d3、d4，這些量分別代表飛行過程中的當地聲速、馬赫數、大氣密度、迎角、側滑角和四個舵偏角，角度單位都為°。用隨機森林模型構建得到飛行器軸向力系數CA和法向力系數CN。

第二步：隨機森林模型構建完成后，通過統計可以得到隨機森林各輸入的節點數目，這代表了各輸入量對于輸出的貢獻程度，因此可以結合森林節點數對各輸入特征進行重要性排序。接下來，將各節點特征依序排列，獲得特征組合的順序。

正如圖9 中所示，針對遙測數據作為輸入的特征排序表明，當地聲速和密度等基礎物理量對隨機森林模型的幫助不大，而馬赫數作為無量綱量對氣動力的預測貢獻較高，這也是符合預期的。具體的特征節點值如表1 所示。

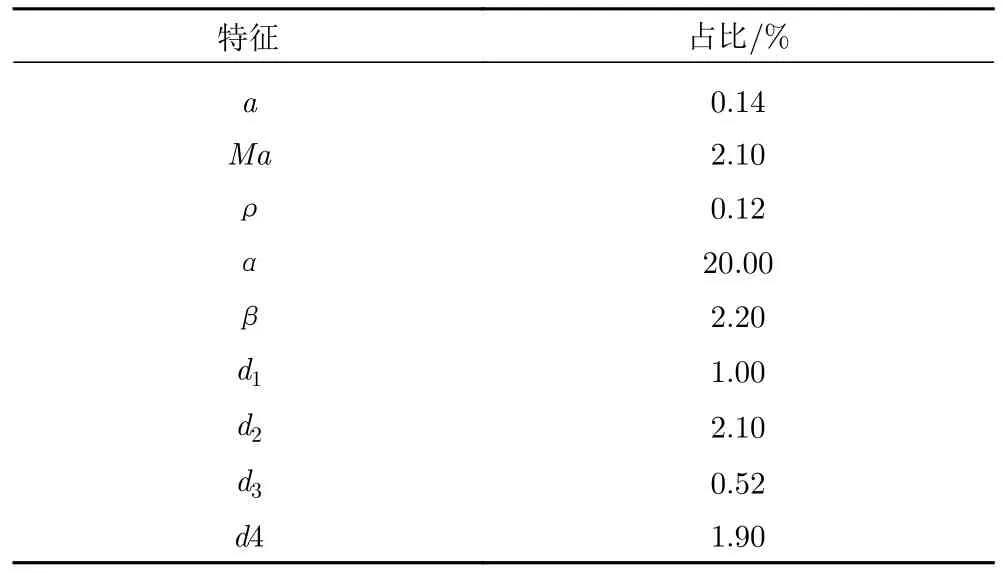
表1 9 個狀態參數特征占比Table 1 Ranking of nine characteristic parameters

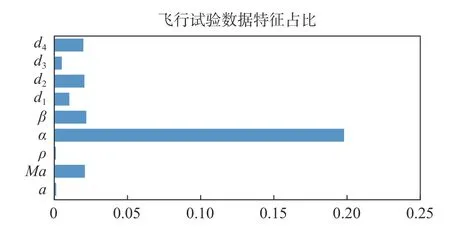
圖9 遙測數據輸入下各特征占比Fig.9 Feature ranking of data from flight test

第三步：融入風洞試驗數據，構建隨機森林模型，定義為隨機森林2。模型在9 個狀態量輸入的架構上增加風洞試驗的法向力系數CN（特征10）和軸向力系數CA（特征11）作為輸入，實現數據融合能力。同時再次進行特征排序，獲取模型主要輸入參數。

模型的特征分析結果如圖10 和表2 所示，可以看到，數據融合的模型結構很大程度上提供了建模時的支撐，風洞試驗數據得到很好體現。特別是法向力系數的占比達到最大，超過了迎角的占比。同時，由于數據融合的模型優勢，隨機森林對高維輸入的模化有著較好的繼承，傳統建模下占優的輸入特征不會因為風洞試驗數據的引入而消退。這也是我們所追求的融合效果。同時可以看到，由于支撐干擾等風洞試驗條件的限制，軸向力系數與飛行的偏差較大，在模型中所產生的貢獻并不明顯，這也是可以接受的。

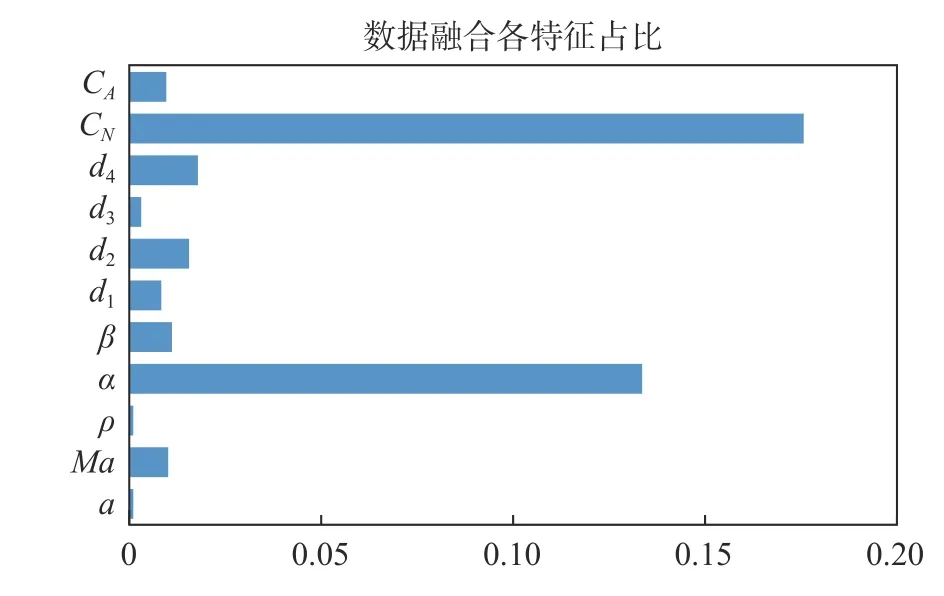
圖10 風洞試驗數據融合架構下各特征占比Fig.10 Feature ranking of data from wind tunnel test

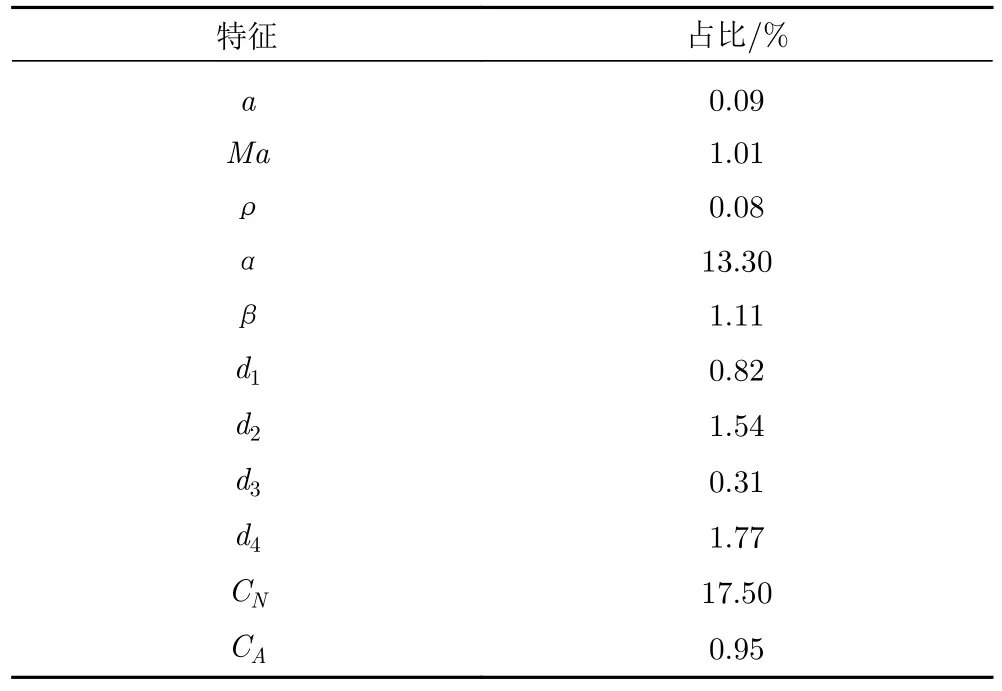
表2 數據融合框架輸入參數特征占比Table 2 Feature ranking of the input data for the data fusion framework

第四步：對比隨機森林模型1 和模型2 的特征重要性，選取特征排序倒數的特征進行特征冗余篩選。每刪除一個輸入特征就需要重新構建隨機森林模型并進行特征排序，直到特征占比最小的值為風洞試驗數據或兩模型占比的最小特征不再相同，這時數據融合模型架構實現最優。因為風洞試驗數據的引入是當前模型所評估的特征中占比的最小值，此時模型的其他輸入不會對風洞試驗數據的融合結果產生負面干擾，最終的數據融合結構也就達到了最優。由于飛行試驗數據中訓練數據的量和數據樣本本身含噪聲特性，對模型的最終建模結果有著主要影響，因此不同訓練數據下模型的架構都有所不同，這里就不再展示模型的最終特征分布結果。

3 飛行試驗天地氣動數據融合結果

針對某對象飛行器飛行試驗數據，開展模型的天地氣動數據融合驗證與特征分析。由于飛行試驗數據涵蓋了復雜的氣動狀態，這里選擇采用同一組飛行試驗數據的交叉驗證來進行模型預測結果分析。

首先針對數據融合策略的有效性進行驗證，選擇50～300 s 的飛行試驗氣動數據開展5 折交叉驗證進行對比。將完整的飛行試驗數據按時間順序等分為5 組，分別針對各部分進行預測，對比數據融合模型和不采用數據融合的模型在相同模型參數設置下的預測精度。對比結果如圖11 所示。

圖11 中黑色虛線代表真實飛行氣動系數的辨識結果，也是我們所需要預測的真實值，而紅色實線代表采用了數據融合模型后給出的氣動系數預測值，而不采用數據融合方法的框架下建模的預測結果用綠色實線表示。可以發現，采用數據融合的隨機森林框架得到了很好的泛化能力和預測精度，在交叉驗證的結果中與真實飛行數據吻合最好。而直接采用遙測數據構建的氣動力模型不能實現有效的氣動力系數預測，這也顯示出數據融合模型給飛行試驗氣動力預測帶來的優勢。

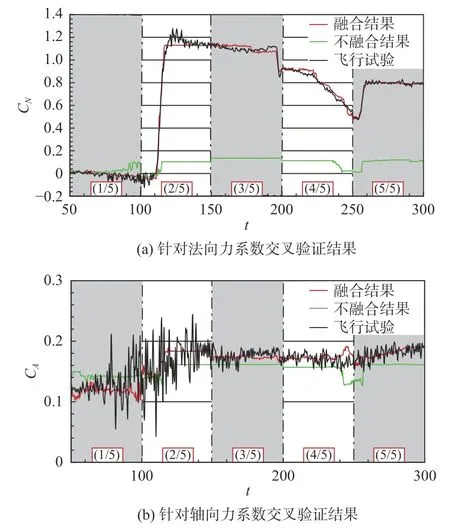
圖11 數據融合模型的有效性驗證Fig.11 Validation of the data fusion model

接下來，選取了訓練預測比約為4∶1 的飛行試驗數據進行氣動預測結果驗證。即采用飛行過程中220 s 的飛行辨識氣動數據構建融合模型，對50 s 的飛行氣動數據進行預測，以此檢測模型對于飛行狀態的外推能力。模型的訓練結果表示為模型擬合的能力，模型的預測結果是指模型對于非訓練狀態的外推泛化能力。

選取了兩個狀態進行氣動預測對比，模型的訓練、預測數據劃分如表3 所示。

表3 訓練預測數據劃分（訓練預測比4∶1）Table 3 Data for training and prediction for case 1 and 2

針對50～100 s 的氣動預測結果如圖12 所示，其中藍色點線代表風洞試驗結果，黑色虛線代表飛行試驗辨識氣動力，紅色實線結果代表隨機森林數據融合模型的預測結果。橫坐標表示為等距時間的數量，這里數據采樣頻率為4 Hz，因此共200 個時刻。當前預測樣本采用100～320 s 的數據訓練模型，可以看到隨機森林模型很好地吻合了飛行試驗結果，相比風洞試驗數據有著較大的精度提高，特別是在法向力系數上，氣動誤差可以降低一個量級以上。

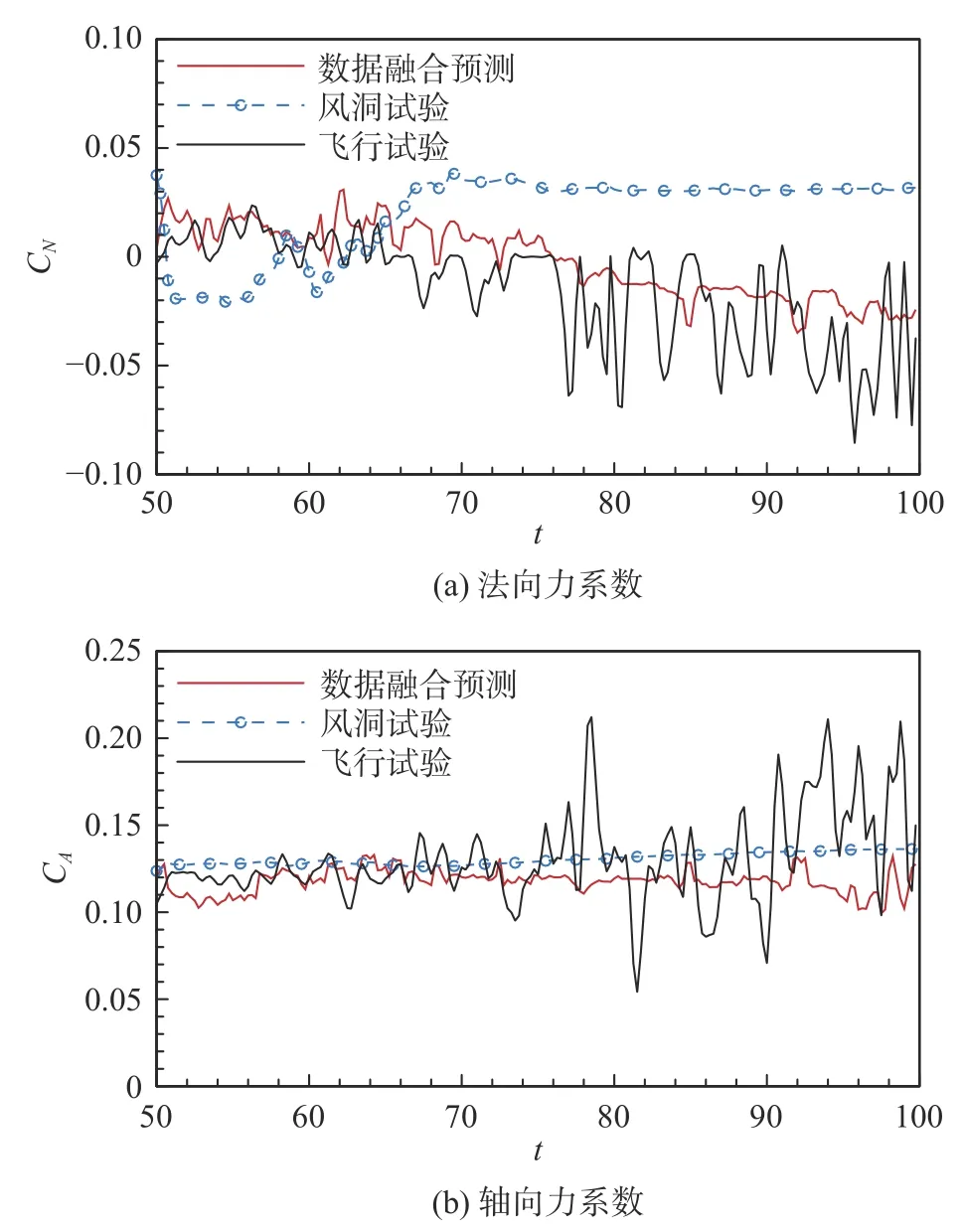
圖12 氣動數據融合模型的預測結果（50～100 s）Fig.12 Predictions of the data fusion model at 50～100 s

針對150～200 s 的氣動預測結果如圖13 所示，隨機森林模型對軸向力系數和法向力系數的預測結果都要遠遠好于風洞試驗。甚至是在辨識結果存在較大噪聲的情況下，模型也識別出了較為精確的氣動力范圍，相比于風洞試驗有著較高的精度。

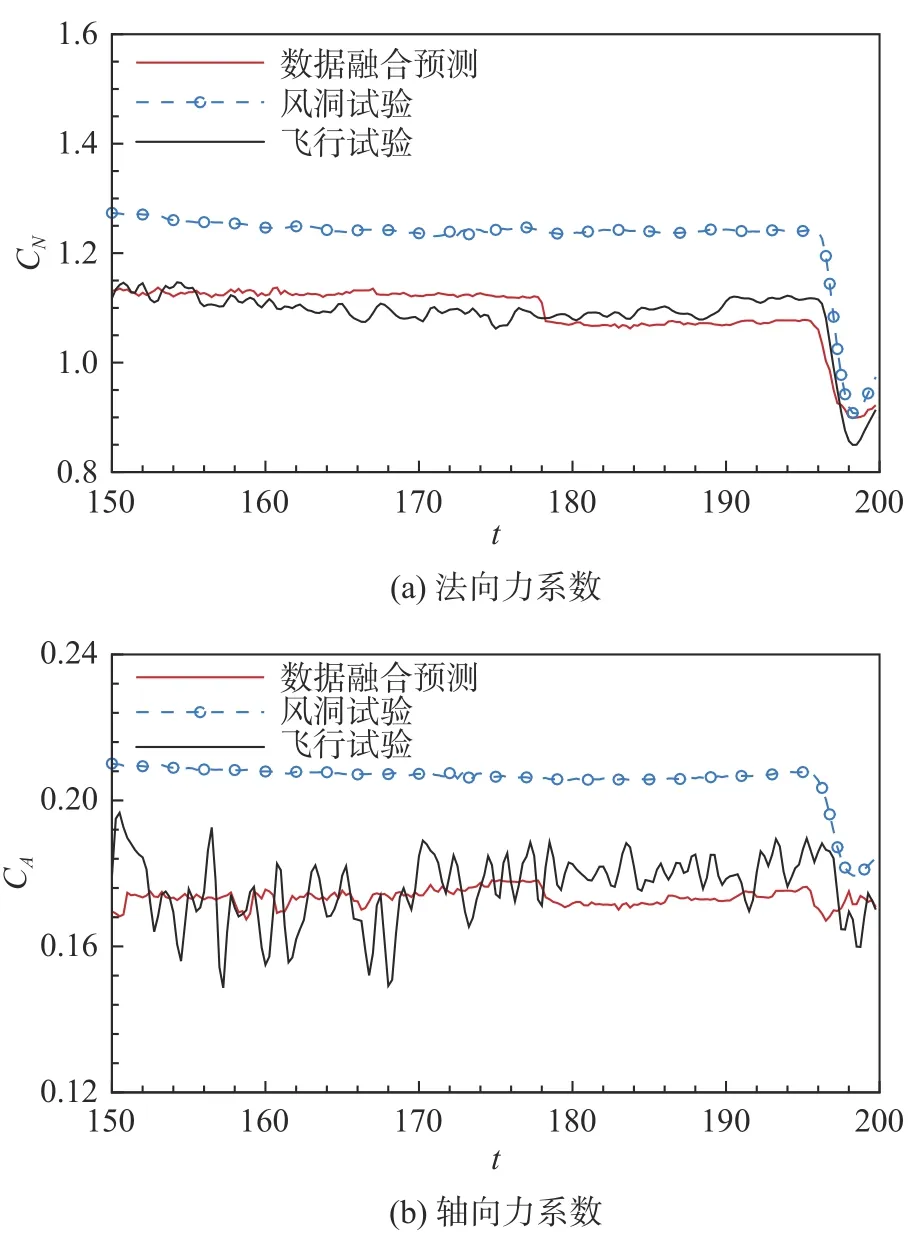
圖13 氣動數據融合模型的預測結果（150～ 200 s）Fig.13 Predictions of the data fusion model at 150～ 200 s

進一步地，為了測試模型對于訓練樣本的收斂性，降低訓練、預測的數據比進行驗證。這次選取100 s 的飛行試驗氣動數據作為測試算例，剩余170 s 飛行試驗數據作為訓練樣本給模型參數訓練，訓練、預測數據比在1.7。算例3 和4 的預測狀態分布如表4 所示。

表4 訓練預測數據劃分（訓練預測比1.7∶1）Table 4 Data for training and prediction for case 3 and 4

圖14 給出了隨機森林模型在130～230 s 飛行區間氣動預測的結果。可以發現，由于訓練樣本的減少，融合模型的精度有所下降，但是相較于風洞試驗結果依然相有著較大的精度優勢。對于法向力系數而言，隨機森林模型在梯度較大值的附近模型存在一定誤差，這是由于試驗數據與飛行數據在這附近的趨勢產生了快速變化，難以通過數據融合模型實現較好的彌補，這也是數據融合類模型的共有問題。

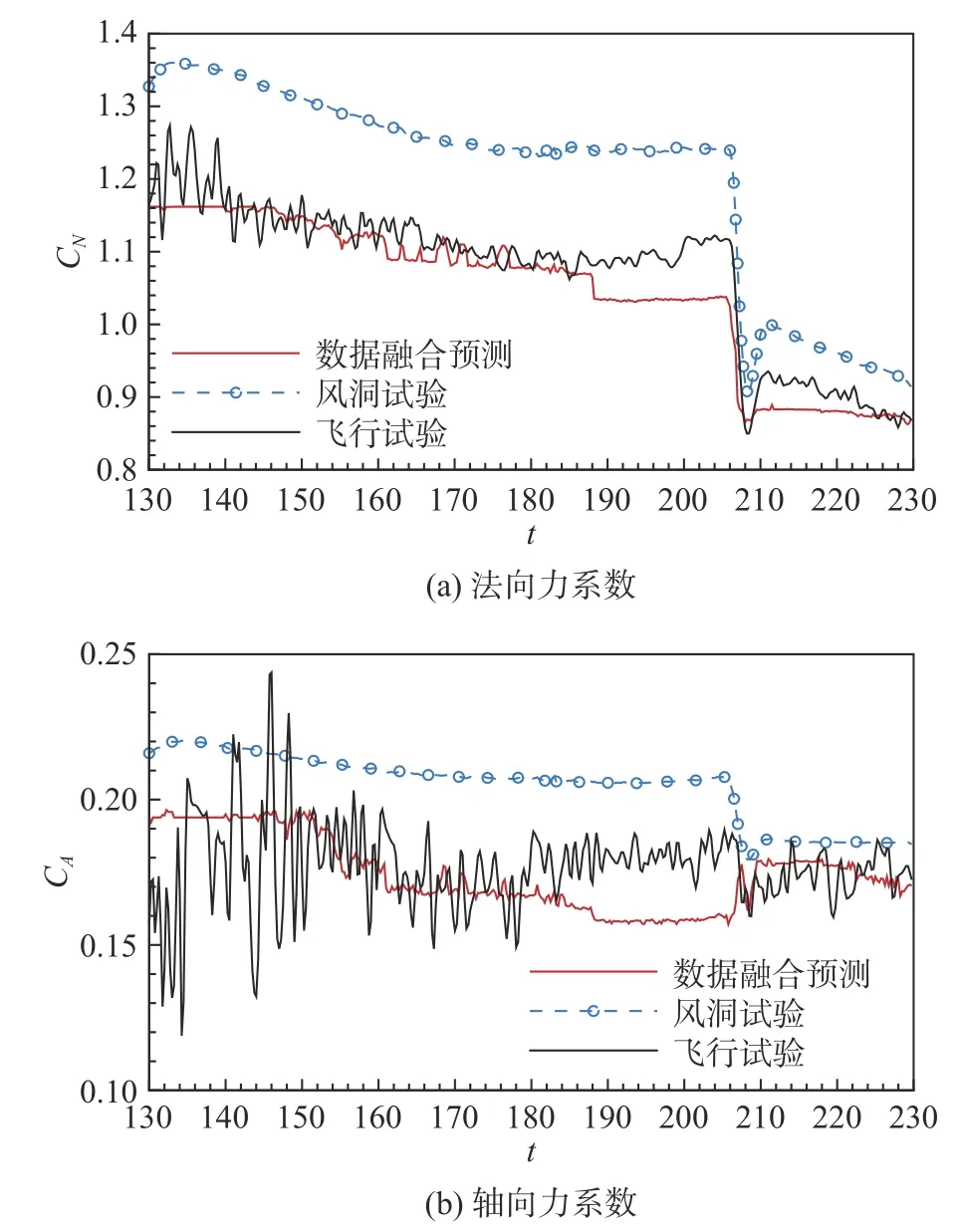
圖14 氣動數據融合模型的預測結果（130～230 s）Fig.14 Predictions of the data fusion model at 130～230 s

圖15 給出模型預測180～280 s 的飛行數據。同樣的，數據融合的隨機森林模型很好地實現了氣動預測能力，在軸向力系數CA和法向力系數CN的預測精度上相較風洞試驗數據均有所提升。以上4 個算例預測結果的均方根誤差對比如表5 所示。

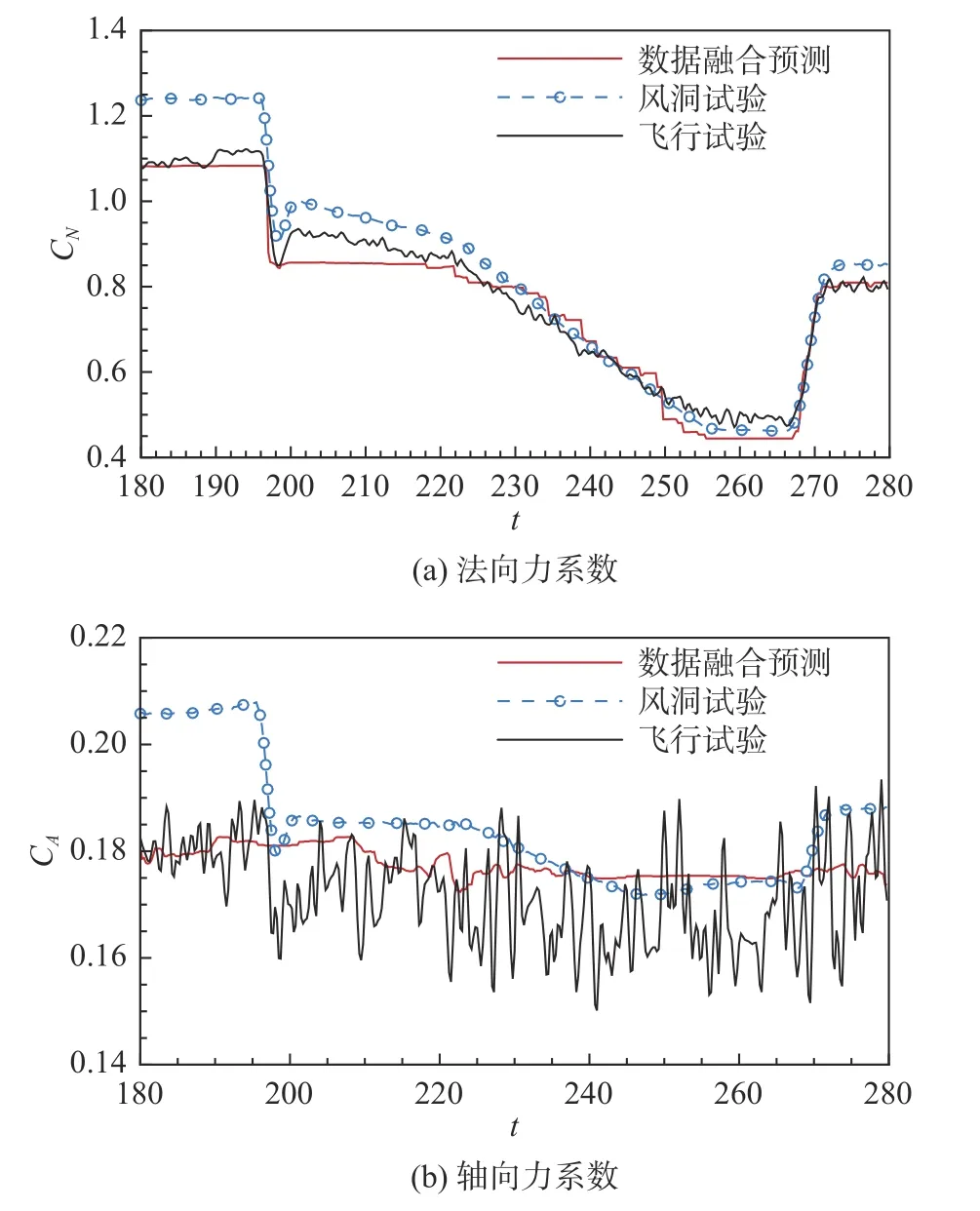
圖15 氣動數據融合模型的預測結果（180～280 s）Fig.15 Predictions of the data fusion model at 180～280 s

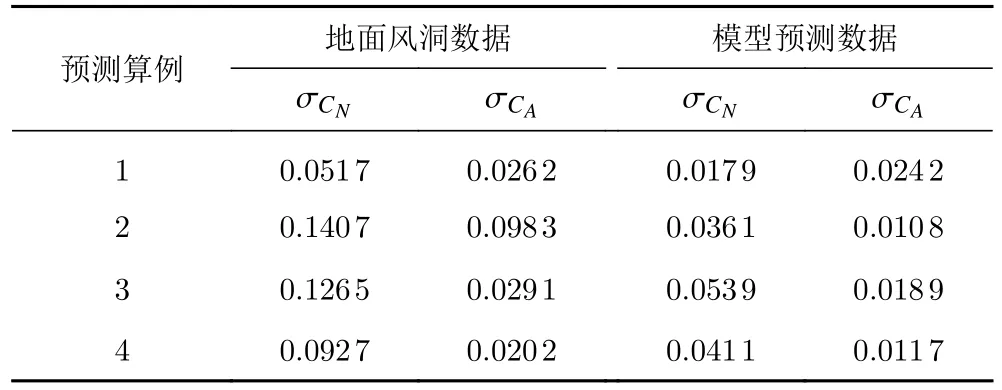
表5 不同預測算例均方根誤差對比Table 5 Mean-square errors of predictions

針對飛行試驗的氣動數據預測結果顯示，數據融合模型可以較好地實現天地氣動數據修正。所提出的隨機森林模型可以自適應地從訓練樣本中挖掘復雜輸入形式下的數據特征，并且實現對不同來流與飛行條件下的多源氣動數據融合。基于隨機森林的數據融合模型可以有效降低天地數據差異，所提供的均方誤差顯示，平均的誤差降低在60%左右。針對訓練預測比的對比情況得出，不同比例的訓練、預測樣本對模型能力有著一定影響。在訓練比為4∶1 時，數據融合模型相對風洞試驗數據的誤差可以降低72%，而當訓練預測比降低后，均方根誤差平均只降低了54%。因此，為了確保模型的有效性在使用前應盡可能進行精度收斂性測試。另外，針對飛行試驗數據的建模體現出很好地抗噪聲能力，在實際工程應用中具備很好的魯棒性。對同一組飛行試驗的交叉驗證測試同時也印證了飛行辨識數據的可靠性，這也作為模型驗證的一部分包含在模型預測精度之中。

4 結論

針對高超聲速飛行器廣泛存在的天地氣動數據差異問題，本文提出了一種面向飛行試驗的多源氣動數據融合方法。結合所提出的隨機森林框架與特征分析回路，實現了不同飛行條件、飛行姿態下試驗氣動數據的高精度預測。針對不同階段飛行試驗數據的驗證表明，所提出的方法具備泛化與外推能力，可以克服一定的噪聲干擾建立數據融合模型。具體結論如下：

1）結合風洞試驗的數據融合框架可以有效修正天地氣動數據差異，降低由于風洞試驗條件帶來的氣動數據誤差，在飛行試驗的不同階段提升氣動數據預測精度。

2）所提出的隨機森林數據融合模型可以很好地降低飛行環境下氣動辨識數據噪聲干擾，實現準確的特征篩選，為高精度氣動模型輸入提供幫助。

3）不同訓練數據與預測數據的比值會影響模型預測精度，應在建模前盡可能進行收斂性分析，以保證模型泛化能力。

目前所采用的隨機森林數據融合模型還沒有開展不同飛行軌跡下的多源融合研究。未來的工作將考慮進一步提升模型泛化能力，推廣應用范圍。同時，針對輸入數據的特征分析有可能進一步揭示天地氣動數據關聯參數的形式，這也將是一個很好的數據融合研究方向。