一種小型碼垛機械臂剛柔耦合動態特性分析

林紅剛，袁銳波，羅 威，陳有錦，朱 正

(1.昆明理工大學 機電工程學院， 昆明 650504；2.光機電液系統集成與控制研究所， 昆明 650504)

0 引言

當今世界，經濟全球化成為時代趨勢，科技的迅速發展，導致國際競爭日益加劇，世界各國都在努力發展經濟。在國家新一輪工業產業升級的背景下，對許多大型港口的吞吐量提出了更高的要求，碼垛機器人作為港口裝卸貨的重要設備之一，國內對其控制算法從未停止研究，但是針對碼垛機器人工況位姿的研究較少[1]。

目前國內對碼垛機器人的仿真研究主要從以下方面進行：簡化機器人機構在Matlab或者ADAMS軟件中進行運動控制和算法分析、對設計的機器人在ANSYS或者ADAMS軟件中進行主要部件的剛性分析、對機器人的關鍵部件在ANSYS和ADAMS軟件中進行剛柔耦合聯合仿真分析。可以發現國內對碼垛機器人的仿真研究漸入佳境，但是針對碼垛機器人在軟件中進行獨立剛柔耦合的工況位姿研究較少。

基于此，本文結合企業生產線的裝載卸貨的工位需求，擬設計一種小型的碼垛機械臂結構，通過在ANSYS軟件中對該機器人在不同工況下進行靜力學與剛柔耦合的對比分析，并分析其運動特性，對機械臂的使用壽命進行下一步的計算具有一定的意義。

1 機械臂的結構及工作原理

根據各行業對機械臂的使用情況，機械臂主要對產品進行轉移，對機械臂的位姿有極高的需求，參考生產線上的具體工作情況，對工作的位姿進行分析，設計了一種小型的機械臂結構。

本文設計的小型機械臂主要由6部分構成[2]。分別是：底座、腰部、小臂、大臂、末端執行器和電機。其具體的組成結構見圖1。

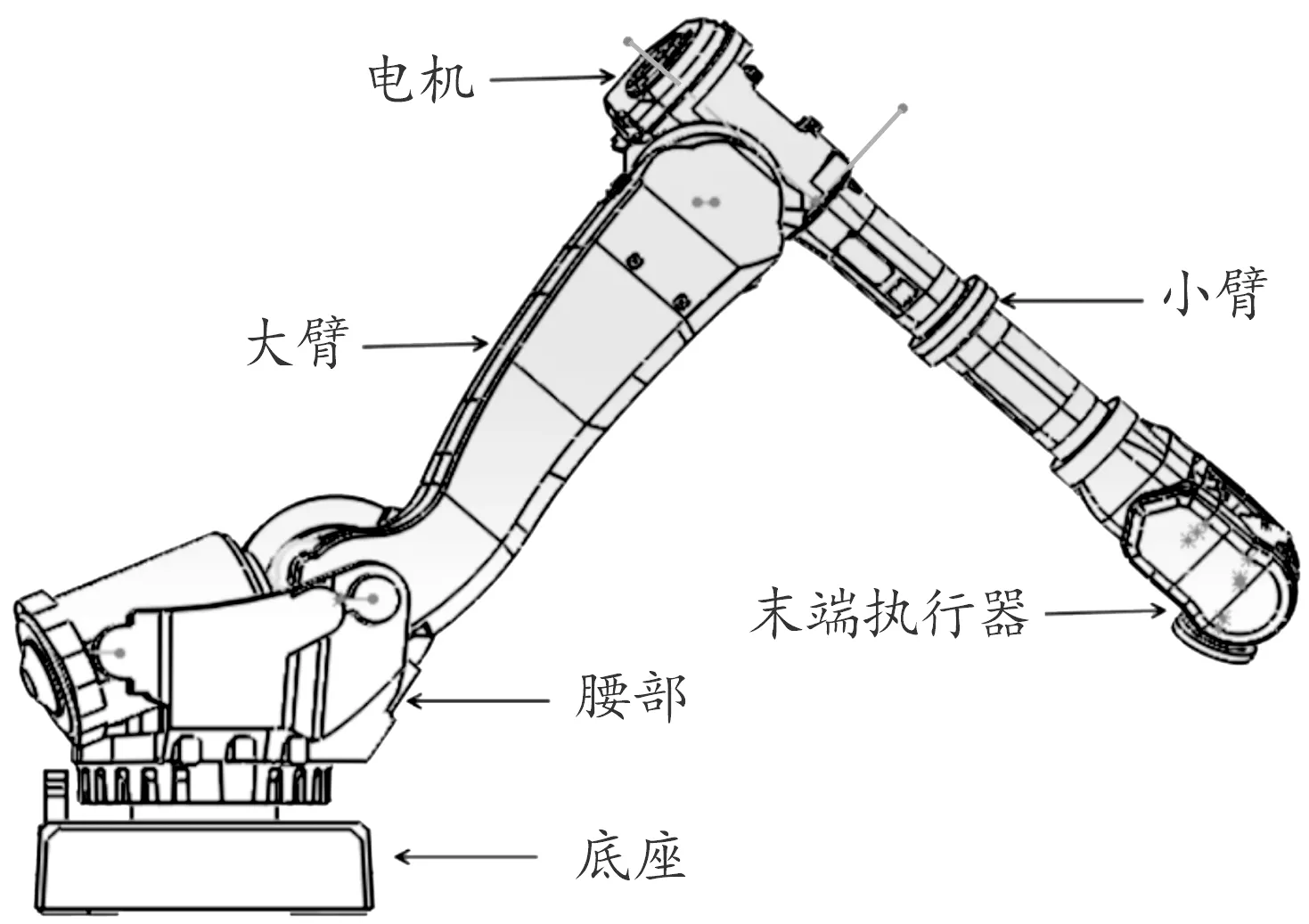
圖1 機械臂的組成結構示意圖

機械臂具體的工作流程為：

1) 底座固定在移動設備上，設置工作參數；

2) 啟動底座電機，腰部零件在底盤和腰部傳動系統作用下繞底座軸線開始旋轉運動；

3) 通過腰部電機與小臂驅動電機可使末端執行器達到機械臂運動空間內的目標位置，機械臂末端執行器最終將產品傳遞到目標位置上。

本機械臂適用于當自動化生產線上產品運輸或者生產結束時，由機械臂將產品轉移和堆放到指定位置。

2 機械臂的運動學模型及位姿空間選取

2.1 機械臂的運動學模型

機器人運動學主要是通過對關節與構成機器人的各個剛體之間的運動關系進行研究。常用的機器人運動學描述方法有D-H參數法與指數積公式法[3]；D-H法作為一種經典的操作臂建模方法，它是關節空間向位姿空間轉換的橋梁，是解決串聯機器人運動學建模問題的重要工具，現已成為現代工業中串聯機器人的主流建模方式。

故本文通過D-H參數法來獲得機械臂的運動學模型。要想推導機械臂關節空間到位姿空間的變換，首先要建立相應的機械臂的連桿坐標系，所需機械臂的連桿坐標系如圖2。

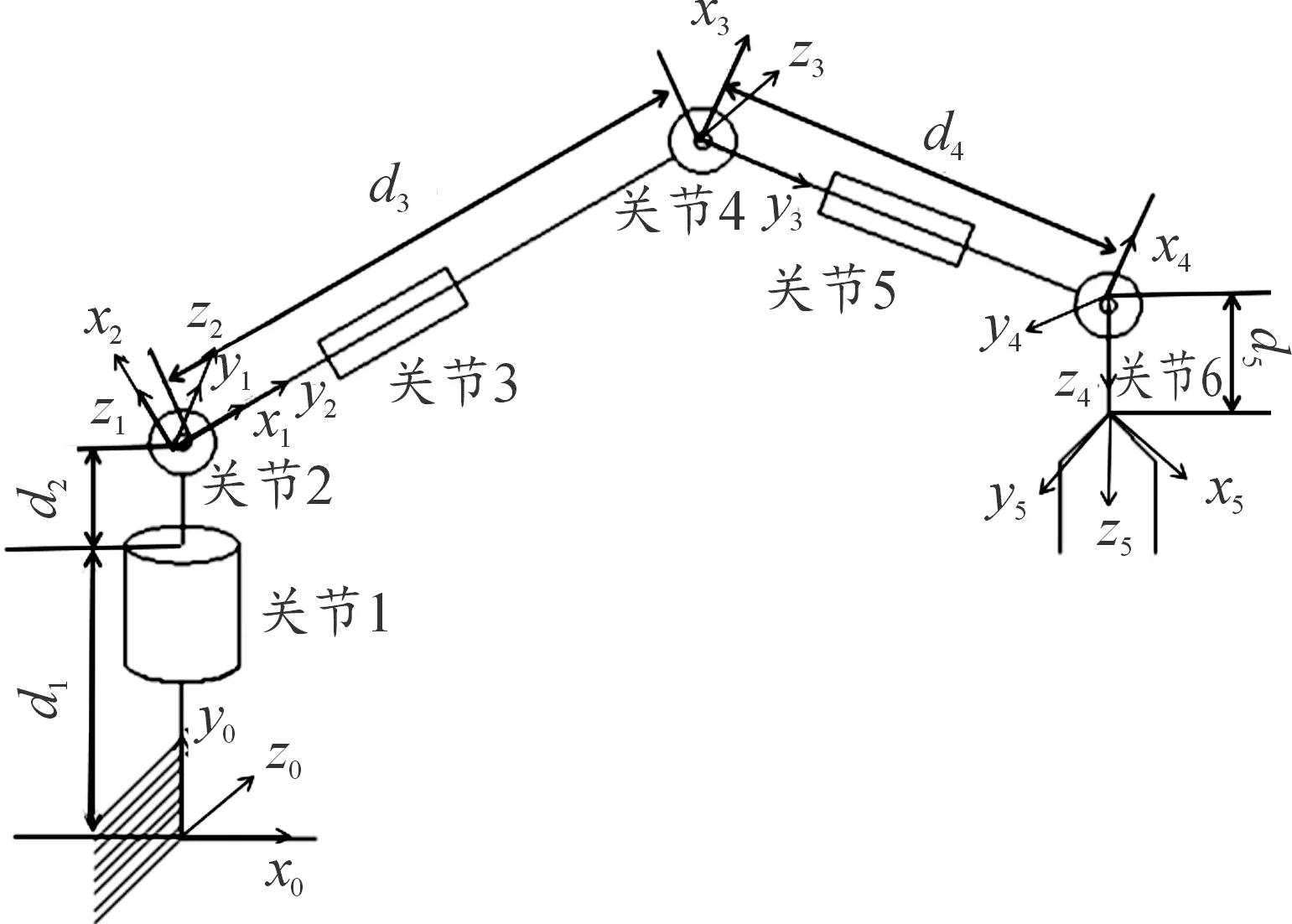
圖2 機械臂連桿坐標系示意圖

參考文獻[3-4]，有機械臂連桿的坐標變換陣的通用算式：

(1)

式(1)中的各個參數所表達的含義如表1所示。

表1 參數定義

結合圖2所示的機械臂和表2的參數，通過將各個參數導入式(2)可以得到各個關節的轉換矩陣，同時得到任意坐標系的姿態。

表2 機械臂連桿參數

表中d1=210 mm；d2=245 mm；d3=1 280 mm；d4=1 365 mm；d5=125 mm。

關節轉換矩陣公式：

(2)

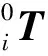
(3)

(4)

(5)

(6)

(7)

其中：ci、si分別代表cosθi、sinθi，i=1,2,…,5。

由以上矩陣可得其相對于基坐標系的位姿矩陣：

(8)

(9)

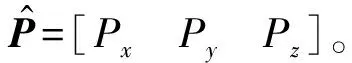
2.2 工況位姿的選取

通過市場調研[5-7]，采用Q235號鋼作為機械臂材料，在機械動力學中，不同的轉角組合對設備模型影響程度是不一樣的，針對其不同工況位姿的要求，對以下3種基本位姿進行了研究。

1) 位姿1：機械臂的腰部繞底座旋轉90°，大臂繞腰部旋轉-30°，小臂繞大臂旋轉25°，到達左右工位。

2) 位姿2：在位姿1的基礎上，機械臂的腰部繞底座旋轉60°，大臂繞腰部旋轉-15°，小臂繞大臂旋轉50°，到達近點工位。

3) 位姿3：機械臂的腰部繞底座旋轉30°，大臂繞腰部旋轉-30°，小臂繞大臂旋轉50°，到達遠點工位。

3 ANSYS靜力學分析

3.1 機械臂模型的假設

對于絕大部分的碼垛機械臂結構而言，它們的結構非常復雜，為了研究機械臂在整個過程中的主要受力情況，本文對機械臂模型作了一些簡化與假設。在ANSYS中對模型做了如下假設[8-11]:

1) 對機械臂內未參與傳動的零部件進行Form New Part操作；

2) 忽略模型的尺寸公差及裝配誤差；

3) 在機械臂的剛柔耦合模型中僅將機械臂大臂進行柔性化，其余的零部件設為剛體。

3.2 ANSYS靜力學仿真

在ANSYS的Static Structural項目里的Engineering Data設置好機械臂各部件需要的材料參數，各構件材料采用236鋼，在 Engineering Data 中設置材料密度為7 850 kg/m3，泊松比為0.3，楊氏模量為2.1×105MPa；然后在Geometry中導入模型并進行假設1的設置，接下來在Model中進行假設3的設置，然后進行材料的添加，對其進行網格劃分。

在完成約束設置后便可對機械臂添加驅動[12-16]，在Model模塊里創建所有連接，固定約束1個，旋轉副3個，接觸形式為摩擦接觸摩擦因子取0.2，機械臂在整個運行周期內，始終受到地球重力的作用，參數為9.8 m/s2，方向負Z軸。同時將其運動過程劃分為啟動、平移、舉起、取料4個階段分析；通過角度驅動的方式進行4個階段的設置，得到如圖3所示的機械臂的剛柔耦合動力學模型的約束設置。

3.3 結果分析

在上述約束條件下進行靜力學分析，求解后得到3個位姿工況全程最大等效應力值分別為 5.358 2、4.938 4、5.085 8 MPa，如圖4所示。出現在大臂和底盤連接部位。根據要求安全系數一般取1.5，根據大臂的安全系數N=σb/σmax，求得N1=44.045，N2=47.79，N3=46.404，完全符合要求。

圖3 機械臂模型的靜態約束設置示意圖

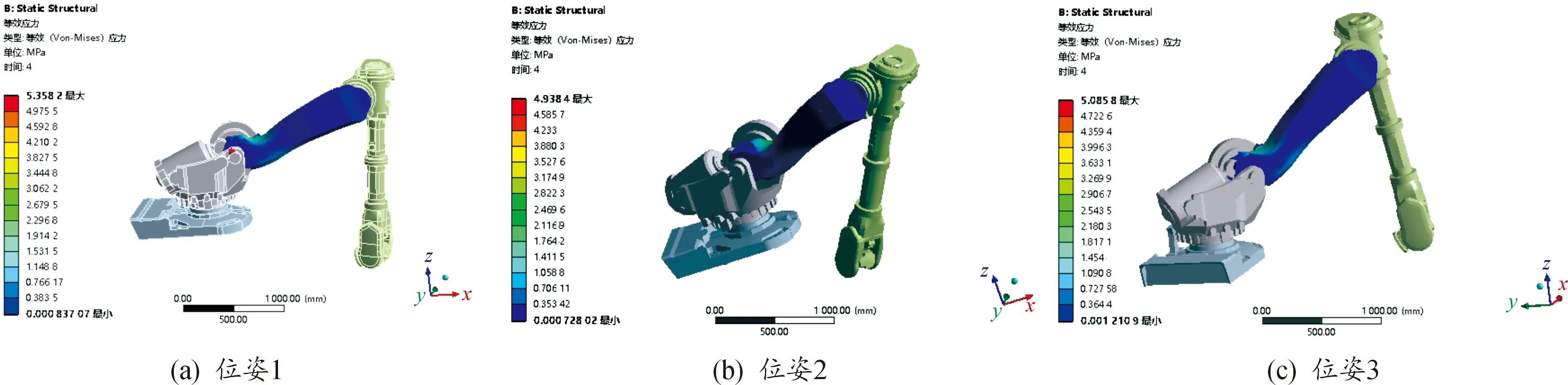
圖4 靜態應力云圖

4 ANSYS剛柔耦合動力學分析

4.1 機械臂模型的建立方式

有很多方式可以建立用于剛體動力學模型，比較常見的剛柔耦合分析步驟：先在ANSYS軟件對柔性體進行網格劃分后保存為.mnf文件，導入ADAMS軟件替換原來剛性的部件，然后進行約束驅動以及求解的設置[17-21]。本文剛柔耦合瞬態動力學分析通過ANSYS軟件進行分析，考慮到機械臂模型結構的復雜性，為了減少多個軟件之間導入導出的誤差，直接在動力學仿真軟件ANSYS中，導入SolidWorks中的剛體動力學模型，具體模型如圖5所示。

4.2 工況的仿真設置

在ANSYS的Transient Structural項目里的Engineering Data設置好機械臂各部件需要的材料參數，然后在Geometry中導入模型并進行假設1的設置，接下來在Model中進行假設3的設置，將機械臂的大臂設置為柔性材料，將其余部件設置為剛性材料，然后進行材料的添加，對其進行網格劃分，共生成 156 148個網格，106 616個節點如圖6。

圖5 機械臂裝配模型示意圖

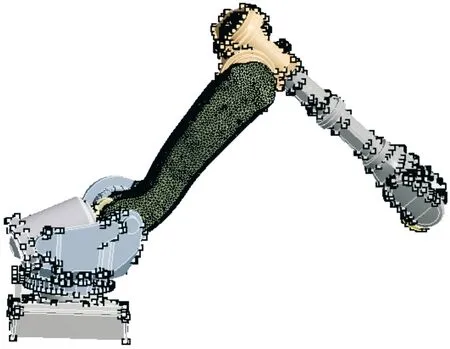
圖6 大臂的有限元網格劃分示意圖

在完成約束設置后便可對機械臂添加驅動在Transient Structural 模塊Model里創建所有連接，設置情況與3.2小節一致；得到如圖7所示的機械臂的剛柔耦合動力學模型的約束設置。

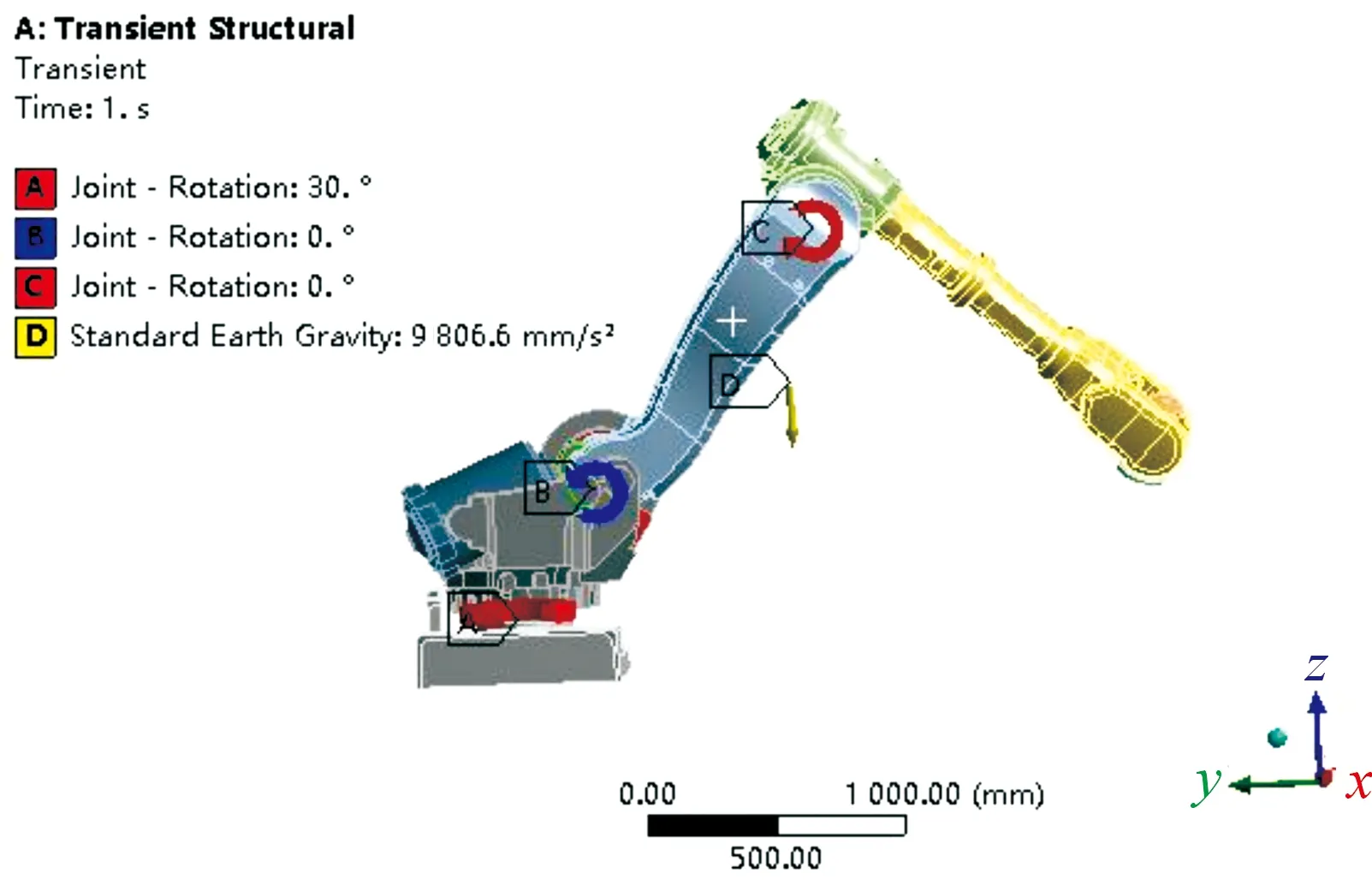
圖7 機械臂模型的約束設置

設置仿真分析時間為4 s，最小步長為0.01 s，通過上述對約束及驅動的設置，便可對機械臂進行仿真。

4.3 結果分析

在ANSYS軟件中按照上述步驟，對比靜力學分析，分別得到3種位姿下的等效應力圖，如圖8所示。在約束條件下進行靜力學分析，求解后得到3個位姿工況全程最大等效應力值分別為19.15、16.05、18.494 MPa。出現在大臂和底盤連接部位。大臂的安全系數N=σb/σmax，求得系數分別為N1=12.324，N2=14.704，N3=12.760，安全系數取1.5，也完全符合要求。

與靜力學分析結果對比，靜力學分析的等效應力結果與瞬態動力學的結果偏差很大，可以發現采用瞬態動力學分析所得到的結果對安全的評估更為精確。

圖8 靜態應力云圖

4.4 運動特性分析

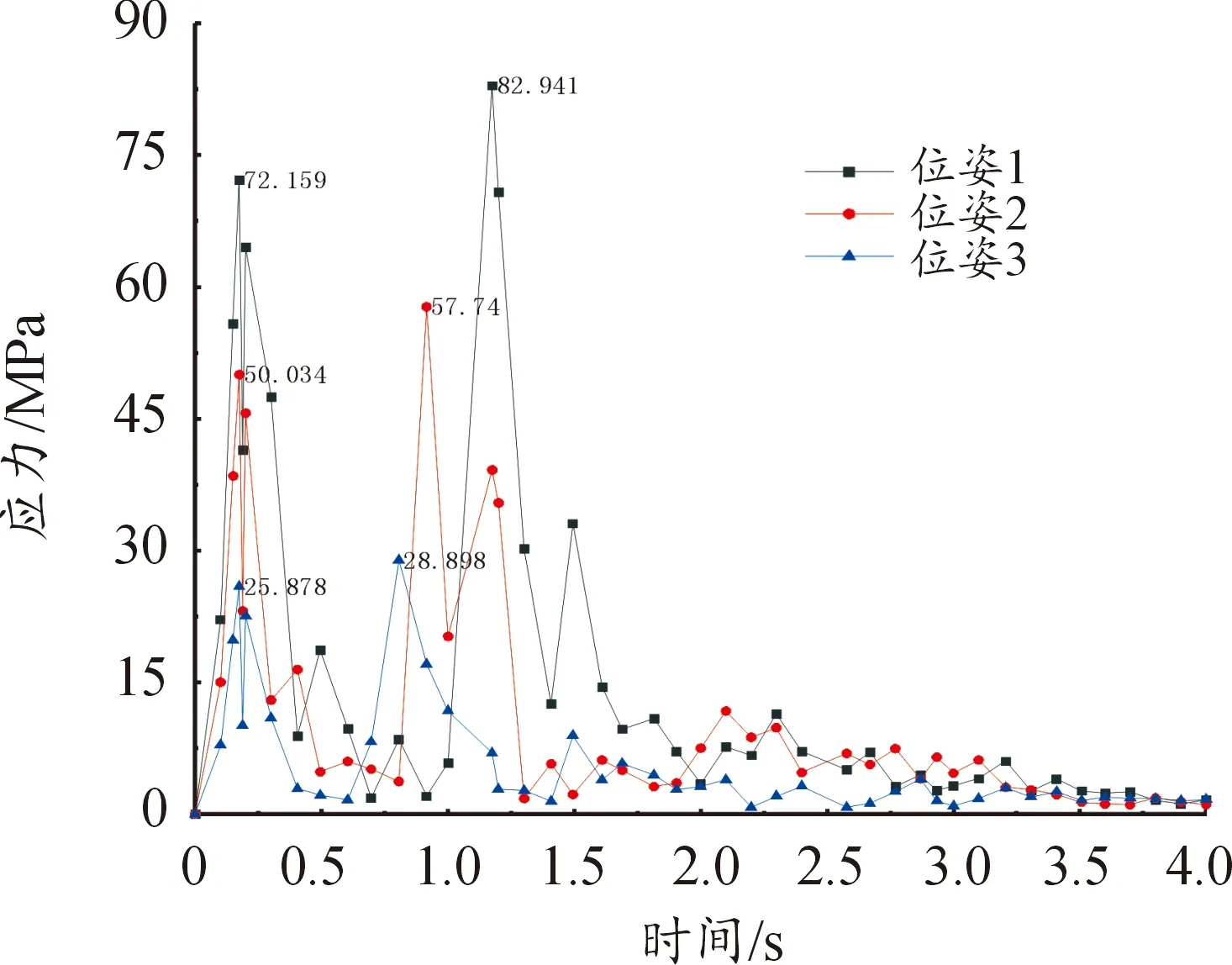
圖9 大臂的受力曲線

從圖9可以看出在相同時間內位姿1的應力最大值滯后于位姿2和3，且出現2個峰值，最后趨于穩定。

圖中可以分析出第一個峰頂是機械臂底盤電機工作時出現，分別為72.199、50.034、25.878 MPa，第二個峰頂是在大臂工作時出現分別為82.941、57.74、28.898 MPa，數據結果表明，機械臂進行作業時，大臂受力最大，在機械臂空間運動情況下，機械臂最容易發生故障。

同時也可以求得機械臂3個位姿工況下的大臂的應力安全系數N=σb/σmax，求得為Nmin=σb/σmax=236/82.941=2.845 4，安全系數取1.5，機械臂仍然滿足材料的要求。

對比采用最大等效應力進行分析，在瞬態動力學分析中，應力最大值為82.941 MPa，與最大等效應力19.15 MPa差值極大。因此，從安全的角度來看，采用全過程的最大應力分析的方法更為精確有效。

圖10 大臂的速度曲線

從圖10可以看出，在相同時間內，位姿1的速度最大值滯后于位姿2和3，隨著工作時間推移，最后趨于穩定。

圖中可以讀出3個位姿的速度峰值分別為2.455 1、1.637、0.819 24 m/s，且達到速度峰值的時間幾乎是同一個時間節點0.25 s，隨著時間推遲，大臂移動速度波動逐步趨于穩定，并且由于速度峰值越大，速度波動越大，趨于穩定的時間越慢。這說明速度移動峰值對大臂的移動穩定性影響較大。

圖11 大臂的位移曲線

從圖11可以看出，在相同時間內,位姿1的位移拐點值滯后于位姿2和3，隨著工作時間推移，最后趨于穩定。同時可以得出，機器人在3種位姿下的最大工作范圍為1 372.7 mm。由此可以進一步對碼垛生產線機器人安裝位置進行設計。

5 結論

1) 與傳統的剛柔耦合分析方法相比，本文所采用的設計思路減少了軟件之間模型轉換的過程，減少了設計周期的時間成本和軟件之間模型轉換的影響誤差。

2) 仿真數據和計算表明：當采用靜力學剛性分析結果精度低，同時采用最大等效應力來分析并不能準確判斷其結構的安全；在一定時間內，速度移動峰值會極大影響大臂的移動穩定性。

3) 通過對比3種工作情況的位姿和最大應力小于材料的屈服強度。且在3種位姿下能達到 1 372.7 mm的工作范圍，本文設計的小型機械臂在進行作業時，滿足工業設計的要求。

4) 考慮到動力學模型輸出特性對接觸剛度非常敏感，一般來說，接觸剛度設置為0.01～1，對輸出結果影響較小，為了提高計算效率，本文僅作常規設置，對接觸剛度與輸出特性的關系有待進行深入探究。