基于隨機模型預測控制的四旋翼無人機研究

李姍姍 龔 薇

(四川大學電氣信息學院 四川 成都 610065)

0 引 言

近年來，由于科學技術的加速發展，無人駕駛飛行器的應用越來越廣泛，如搜索救援任務[1-2]、火災監測[3]、邊境巡邏[4]、作物監測[5]和基礎設施檢查[6-8]等。而四旋翼飛行器憑借其具有懸浮、高機動性和簡單設計的特性，成為最常用的飛行器之一。然而，盡管它們具有巨大的應用潛力和操作自主性，但從技術演示到實際應用的轉變卻是一個緩慢的過程。造成這一重大差距的原因在于無人機飛行器實際操作中通常會受到干擾的影響，為了保證飛行可行性，如何處理干擾是無人機飛行器的首要考慮之一，也是目前的重大挑戰之一。

在過去的幾十年中，已經發表了許多關于四旋翼動態建模的文章[9-11]。Mistler等[12]首次將反饋線性化方法應用于四旋翼飛行跟蹤參考軌跡。Bouabdallah等[13]比較了兩種基于模型的直升機穩定性控制技術的性能:一種采用簡化動力學的經典PID方法和一種基于更完整模型的現代LQR技術。Castillo等[14-15]給定四旋翼的位置，并應用嵌套飽和控制來穩定其姿態。Xu等[16]提出了一種滑模控制器來穩定一類級聯欠驅動系統。另一種常見的控制方法是逆步進技術[17]。

然而近幾年計算機計算能力的增強，使得先進的控制器成為可能。在這種情況下出現的一個突出的控制策略是模型預測控制(MPC)。回溯到20世紀70年代末，模型預測控制在最初的構想是控制化學工業過程[18]，它通常具有緩慢的動力學和以秒或分鐘計算的采樣時間。由于當今的高性能處理器，MPC已經被應用于四旋翼飛行器中的快速系統。2013年Subbarao等[19]根據一個四旋翼的線性化模型建立了一個MPC模型。建立的控制器可以跟隨軌跡，同時能處理對飛機方向施加的限制(滾軸和俯仰角)。但這種方法無法處理系統中存在的不確定擾動，一種常用的處理擾動的方法為魯棒模型預測控制，但這種方法可能由于過度保守而無法解出可行解。一種自然而然的想法便是放寬約束，使約束在一定概率內滿足，這種考慮導致了隨機模型預測控制(SMPC)的出現，該方法可以使系統在滿足約束與控制性能之間進行權衡，這導致系統控制性不再那么保守。

實際上，在無人機飛行中，可以找到多個擾動源，如位置或速度測量誤差、電機速度失調，甚至大氣阻力，以及一些未知分布的隨機擾動。本文在只知道擾動一階矩及二階矩的情況下，提出一種SMPC控制方案，實現在一定程度上滿足約束。擾動的處理采用分布式魯棒方法求出其模糊集，再針對軟化后的單輸入約束與聯合狀態約束進行分別處理。前者采用最壞情況下的條件風險值約束進行等價轉換，然后運用定理等價為可計算的半定規劃(SDP)凸優化約束。后者采用布爾不等式將聯合約束轉換為多個單狀態約束，再運用凱特利切比雪夫不等式將非凸約束轉換為凸約束。計算過程中采用了在線擾動反饋，該方法可解決狀態反饋存在的非凸問題。針對該算法，本文在末尾進行了凸優化可計算分析以及可行性穩定性分析，證實了該算法的可計算性、可行性與穩定性。

1 四旋翼無人機的模型和問題描述

1.1 四旋翼無人機的線性模型

在本節中，我們通過轉換地面坐標系原點與機體坐標系原點對四旋翼無人機建立力學研究坐標系(如圖1所示)，并建立了四旋翼無人機的六自由度動力學模型，將其應用于控制器的設計中。基于結構建立的模型可以顯著提高設計和測試效率，對控制系統的設計和性能分析具有重要的意義。

圖1 四旋翼無人機坐標系統

通常，四旋翼無人機被建模為一個具有6個自由度[x,y,z,φ,θ,φ]的剛體，其中：x、y、z分別表示笛卡爾坐標系中的狀態；φ、θ、φ分別表示俯仰角、旋轉角與偏航角。

式中：b和d分別表示推力系數和阻力系數。則其非線性動力學模型可以由歐拉-拉格朗日方程[13-14]推導得。

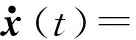
假設無人機在近似懸停狀態時，該動力學模型可以由一個線性的模型來近似，在工作平衡點附近使用一階泰勒展開[20]，最終轉化成線性離散狀態空間模型為:

(1)

1.2 約束條件

如上所述，四旋翼無人機的動力學模型有6個輸出[x,y,z,φ,θ,φ]，四個獨立的輸入[Ω1,Ω2,Ω3,Ω4]。由于四旋翼的欠驅動性質，在[x,y,z,φ]達到理想位置時，只需[φ,θ]保持穩定[21]。因此需要限制它們的振幅。這些約束能被表示為:

φmin≤φ≤φmax

θmin<θ≤θmax

這些約束可由線性不等式約束集合定義的凸區域Fx定義為如下形式：

(2)

在實際飛行中，馬達轉速也會受到電壓的限制，則控制輸入受到約束，可表示為:

u≤umax

同理，控制輸入可表示為如下線性不等式描述的凸可行區域Fu:

Fu={u|Hu≤h}

(3)

其中，系數H與h定義如下：

2 模型預測控制算法的重構

2.1 模型預測控制的系統模型

在有限時間的最優控制中，假設模型是從t到t+N求解優化問題，其中N為預測視界。定義狀態、輸入、擾動與輸出的緊湊模式如下：

(4)

則式(1)可轉換為如下緊湊形式：

(5)

式中：C∈RNq×Nn，主對角線值為C，除主對角線外均為0；A、B、D和G可參考文獻[22]，文獻中展示了詳細推導過程。

同理，由定義(4)可將式(2)與式(3)轉換為如下緊湊模式:

式中：ai∈R(N+1)q，bj∈R，H∈RNu×Nm,h∈RNm。由于擾動的分布未知且無界，不能保證約束總是能得到滿足，因此可允許一定概率違反約束。在這種情況下，通過考慮系統中存在不確定性的所有可能性，可在系統性能與約束滿足之間進行權衡。將Fx與Fu替換為如下概率約束：

P(x∈Fx)≥1-δx

(6)

P(u∈Fu)≥1-δu

(7)

式中：δu∈(0,1)、δx∈(0，1)分別表示輸入與輸出最大的違反概率。對于線性問題，常定義如下二次函數為目標函數：

(8)

(A+BK)TQN(A+BK)-QN+Q+KTRK=0

故重構后的四旋翼無人機的目標跟蹤問題P1如下：

minVN(xt,u,w)

(9)

s.t.x=Axt+Bu+DGw

y=Cx

P(x∈Fx)≥1-δx

P(u∈Fu)≥1-δu

2.2 擾動反饋重構

由于控制輸入u應該是具有當前和過去狀態的某種反饋控制策略，故常采用反饋結構定義控制策略u。以往反饋形式常采用狀態反饋參數化，但預測的輸入序列和狀態序列是狀態反饋增益序列的非線性函數，故一般情況下，可行決策變量集是非凸的。另一種可計算的凸優化反饋控制策略為放射擾動反饋參數化[24]。

(10)

式中：Mi,j∈Rm×n，vi∈Rm。在相關文獻中，這種擾動反饋控制策略被證明與狀態反饋控制策略是等價的[24]。同理，式(10)可以表示為如下緊湊形式：

u=MGw+v

式中：M∈RNm×Nn，v∈RNm，其具體形式與推導過程可參考文獻[24]。將反饋結構加入P1，可轉換為如下P2問題:

minVN(xt,u,w)

s.t.P(HMGw+Hv-h≤0)≥1-δu

1-δx

3 約束的重構

3.1 擾動的重構

式中：E[P][·]表示在分布下P的期望，μ=1N?μ0，Σ=IN?Σ0，μ0為擾動均值，Σ0為擾動方差,?表示克羅內克積，分別定義為E[ωi]=μ0，Σ[ωt]=Σ0且均已知。

在分布P未知的情況下，通常式(7)的可行集為非凸的，有時甚至是不連通的。對概率分布中不確定性處理的一種常見方法是采用分布魯棒方法[25]，定義分布魯棒的輸入機會約束與聯合狀態約束如下：

處理后的輸入與狀態約束再分別采用合適的方法進行精確凸重構。

3.2 輸入約束的凸重構

眾所周知，魯棒的單機會約束可以被最壞情況下的條件風險值約束保守地近似，且在文獻[25]推理2.1中，證明了當原硬約束為擾動的仿射函數時，該近似是等價的。故上述單輸入約束可等價為如下最壞情況下的條件風險值約束：

P-CVaRδu(Hv-h+HMGw)=

式中：P-CVaRδu(a)為δu概率下滿足條件a的概率。并且根據文獻[25]，可將單輸入最壞情況下的條件風險值約束等價為如下可計算的SDP約束：

其中：trace(a)為求矩陣a的跡；N為優化的變量。

SDP模型在計算時通常比較復雜。SOCP模型是SDP模型的特例，但變量更少，算法效率更高，故將上述SDP約束轉換為如下SOCP約束的形式，提高計算效率[26]：

(11)

3.3 聯合狀態約束的隨機模型預測控制重構

由于聯合狀態約束需要在不確定性分布上求解多元積分，導致其求解過程十分棘手，且通常為非凸約束。為了得到一個近似可處理形式，常采用布爾不等式進行轉換。首先，需要將狀態魯棒機會轉換為上確界形式。

再應用布爾不等式得到如下轉換：

式中:δxx=δx/l為輸出最大違反概率δx的l次均值分配，這種固定風險分配可避免優化算法的非凸性。轉換后的分布式魯棒聯合狀態約束可轉換為如下形式的保守逼近：

(12)

運用坎特利凱特利切比雪夫不等式，可將式(12)固定風險分配后的狀態約束轉換為如下可計算的凸優化形式，近似文獻[27]引理4.1。

在本文中，由P2可知l=2。單輸入約束與聯合狀態約束經過一系列轉換，均近似成可處理的凸約束。重構后的P2問題可以轉換為如下的P3問題：

minVN(xt,u,w)

(13)

4 系統性能分析

4.1 系統的可計算分析

顯然，在P4問題中，目標函數與單輸入約束都是凸的線性約束，但聯合輸出約束中，由于Σ[x]的存在，使得狀態約束在CVX包中不可計算，故將其進行如下轉換：

ζi=BMGΣGTMTBT+DGΣGTDT+

BMGΣGTDT+DGΣTGTMTBT

此外，為了保證在任意狀態輸入的情況下，均存在可行解，可在目標函數中引入了松弛變量，結合式(11)與式(12),P3問題可以轉換為如下P4問題：

mint

s.t.VN(xt,M,v,w)≤t

4.2 可行性與穩定性

因為無界擾動的存在，使狀態保持在硬約束系統的可行域中是不切實際的。本文通過軟化約束以及加入松弛變量等方法解決了該問題。只有當違反約束時，松弛變量才是非零的，其余情況松弛變量則保持為零。這種精確罰函數方法可以使軟化約束的解集與原硬約束的解集等價，即針對一個初始狀態，原硬約束問題不可行時，新構建的軟約束問題卻可以產生一個可行的終端解集，且該解集與原硬約束問題可行時解出的解集是相同的，而這種思想保證了系統的可行性。

當矩陣A為舒爾穩定時，文獻[27]已證明其穩定性，接下來我們證明當A為李雅普諾夫穩定時系統的穩定性。

系統李雅普諾夫穩定時，存在一個坐標變化，使系統分解為如下形式：

式中:A1為舒爾穩定部分，A2特征根在單位圓上，具有相同的代數和幾何多重性。假設A2為對矩陣角，且主對角線上元素要么為±1，要么為2×2的旋轉矩陣，因此A2為正交矩陣。

對于任意ε>0，考慮如下“負漂移條件”：

此外，不難得到以下關系成立：

由于控制與擾動的一階矩均有界，故存在常數M滿足:

5 仿 真

在本節中，為測試幾種控制策略對軌跡跟蹤問題的性能，進行了如下數值模擬。仿真中使用的模型參數如表1所示。

表1 四旋翼無人機的參數

無人機到達目標點的順序參考如下：

(0,0,0)→(0,0,5)→(5,0,5)→(5,10,5)→

(-5,10,5)→(-5,0,5)→(5,0,10)

考慮初始狀態為[x,y,z]=[0,0,0]，角度狀態為[φ,θ,φ]=[0,0,0]，采樣時間τs=50 ms,懲罰權重Q=10I12，R=0.01I4。為了加強飛行的穩定性，分別對姿態和輸入進行了約束，姿態約束為：φmin=-0.5,φmax=0.5,θmin=-0.5,θmax=0.5輸入約束為：umax=[250,250,250,250]，則仿真結果如圖2-圖4所示。

圖2 無人機在不同擾動下的位置變化

圖3 無人機在不同擾動下θ的穩定情況

圖4 無人機在不同擾動下Φ的穩定情況

由圖2可以看出，在不同擾動相同步數的情況下，系統仍然可以實時有效跟蹤，但隨著擾動的增大，距離規定點的誤差越大。圖3-圖4顯示不同擾動下俯仰角Φ與旋轉角θ均可保持穩定。

圖5-圖8展示了MPC[21]與SMPC性能對比。圖5顯示在相同步數的情況下，SMPC不僅能克服隨機擾動，而且在反饋的作用下反應速度更快，比無擾動的MPC更快到達每一步的終點。圖6-圖8顯示SMPC算法能夠在滿足系統約束的情況下克服隨機擾動實現目標跟蹤，且消耗燃料與無約束的MPC算法相差無幾。

圖5 兩種算法下的位置變化

(a) MPC

(b) SMPC圖6 兩種算法下θ的穩定情況

(a) MPC

(b) SMPC圖7 兩種算法下Φ的穩定情況

(a) MPC

(b) SMPC圖8 兩種算法下的輸入

圖9展示了不同預測步數對SMPC算法的影響，可以看出，當增大SMPC的預測步數時，相應速度也可以增加得更快，穩定性也會更好。圖10展示了不同輸入對SMPC算法的影響，可以看出，當初始狀態不同時，系統均可解出優化解完成路徑跟蹤。

圖9 不同預測步數下的位置變化

圖10 不同初始狀態下的位置變化

6 結 語

針對四旋翼直升機的穩定性和航跡跟蹤問題，本文提出一種隨機模型預測控制器。在利用隨機模型預測技術進行四旋翼無人機控制的相關工作中，該方案的主要優點在于：1) 具有處理系統不確定性擾動的能力；2) 考慮擾動反饋下的輸入約束與聯合狀態約束；3) 運用近似等價的方法對軟輸入約束與聯合狀態約束進行凸重構；4) 運用機會約束與松弛變量保證了系統在不同初始狀態下均有解集，且與原硬輸入解集相同。在仿真實驗中，我們將SMPC的性能與MPC方法進行了比較，結果顯示本文方法能夠更好地處理擾動且具備更優秀的預測性能。