基于CHAN 的改進卡爾曼濾波室內定位算法

蔣銳，虞躍，徐友云，王小明，李大鵬

（1.南京郵電大學通信與信息工程學院，江蘇 南京 210003；2.南京郵電大學通信與網絡技術國家工程研究中心，江蘇 南京 210003）

0 引言

隨著科技的發展，各種無線通信系統相繼出現，這使以通信為基礎的導航、定位等技術迅速發展。全球定位系統（GPS,global positioning system）是一個由24 顆衛星組成并覆蓋全球的衛星系統[1]，在室外空曠地帶定位效果很好。但是GPS 信號的接收功率很小，并且在有障礙物遮擋時會出現很大的誤差，因此并不適用于室內定位。針對這一問題，各種室內定位方案也相繼出現，常見的方案有藍牙定位、無線局域網定位、紅外線定位、超寬帶（UWB,ultra wide band）定位等。

藍牙定位技術[2]是比較主流的定位技術，在綜合成本、抗干擾能力和布局復雜度上有一定優勢。但是，其定位誤差一般在1～3 m，不適合對定位精度要求較高的室內場景。無線局域網定位技術[3]通過采集網絡節點位置信息，完成對目標位置的定位。目前，室內無線局域網布置廣泛、應用場景較多，這是其優勢所在。但是無線局域網信號容易受到干擾并且能耗較大，因此定位精度較低、定位穩定性較差。紅外線定位技術[4]利用光學傳感器接收定位目標發射的紅外線進行測距，并實現對目標定位。但是紅外線只能沿直線傳播，不能穿透遮蔽物，其在室內復雜環境下的定位效果不佳。UWB 定位技術[5]是一種無線載波通信技術，頻率帶寬在1 GHz 以上，范圍在3.1～10.6 GHz。UWB 信號發射不需要使用傳統通信體制中的載波，而是通過發送納秒級及以下的極窄脈沖來傳輸數據[6]。UWB 定位是通過計算脈沖到達時間完成對距離的測量，從而實現目標的定位。與其他室內定位技術相比，UWB 信號具有很高的頻率和時間分辨率，使多徑信號在時間上不容易重疊，方便接收機分離多徑信號分量并充分利用，提升定位精度。因此，UWB 定位精度可達到分米級，且抗干擾能力及抗多徑衰落能力強[7]。本文在復雜室內環境下，選取其作為定位算法的實現方案。

文獻[8]提出了具有閉式解的二步加權最小二乘算法，即CHAN 算法。該算法本質上是利用最大似然估計求出目標節點的位置信息，充分利用了冗余信息。同時，該算法定位精度較高，當基站數大于3 時接近定位估計的克拉美羅下界（CRLB,Cramer-Rao lower bound），也是使用較廣泛的定位算法。該算法在推導過程中存在一個前提條件，即假設測量距離誤差較小且為理想的零均值高斯隨機變量。所以在一些復雜定位環境中，該算法定位精度較低。

為了降低室內定位中非視距（NLOS,non-line-of-sight）誤差帶來的影響，可以利用信號反射的幾何性質推算出信號的反射路徑。該類算法首先通過發射角和入射角將NLOS 信號的反射點估算出來，然后推算出信號傳輸的實際路徑，最后計算出目標與基站間的直射路徑長度。通過提高發射角、入射角的精度和單反射圓模型的準確度，可以實現對目標的高精度定位[9-10]。另外，由于直射信號在穿透室內常見障礙物時產生的損耗是不同的，比如鋼板、人體和木板等情況產生的穿透損耗是不一樣的。因此在確定具體障礙物的類型、厚度和數量等信息的情況下，對信號在穿透障礙物時造成的能量損耗逐一進行校準和對比分析，可以準確地計算出信號直射距離[11-12]。

以上2 類室內定位算法雖然可以在復雜室內環境下將定位精度提高到30 cm 左右，但是需要提前知道室內障礙物的位置、類別、數量等信息，因此在實際場景中較難應用。在實際應用中，一般對NLOS 信號誤差本身進行處理，從而優化定位結果。殘差檢驗算法在觀測定位突變數據時計算殘差并設置一個閾值，若產生的殘差大于閾值，則視為NLOS 信號，并進行丟棄；否則，視為視線線路（LOS,line of sight）信號，可以加以利用并實現目標定位。但是該算法在存在大量NLOS 信號時無法對目標進行定位處理[13]。中值濾波算法對NLOS觀測值進行預處理，將某一距離量進行多次觀測量，加權去除其中的最大值和最小值，將剩余的測量值進行均值濾波作為該處距離的觀測量。在實際場景中，一個位置處于NLOS 的情況很可能一直存在，對某一個點的多次觀測量會一直存在較大誤差，這也是該算法需要優化解決的問題[14]。文獻[15]假設在每次進行觀測時，當前標簽（Tag）的位置離前一時刻標簽的位置應該保持低于閾值。基于以上假設，在多基站定位情況下可以對定位基站進行分組，取任意3 個基站為一組，將每組計算結果與上一時刻標簽位置之差在給定閾值內的所有結果進行加權平均處理，計算出當前時刻的標簽位置。該算法考慮定位結果的時間關聯性，當存在至少一組基站與標簽之間為全LOS的情況時，該算法性能可達到30 cm 左右的定位精度。但是在實際環境中，很難保證基站和標簽之間的信號傳輸情況，所以在復雜室內條件下，其定位性能急劇下降。

文獻[16]利用卡爾曼濾波來修正CHAN 算法在NLOS 下產生的距離誤差值。其核心思想包括定位結果的預測和校正2 個階段，其中，預測階段是根據前一時刻系統狀態的估計值，計算當前時刻系統狀態的預測值；校正階段是獲取當前階段的觀測值，對預測值進行修正，從而給出當前時刻系統狀態的最優估計。同時，該算法隨著定位時間的推移，會不斷改善卡爾曼濾波增益系數K來達到精準定位的效果。但是在初始定位階段，由于增益系數K調節較慢，會使其在初始時刻定位精度不高，并且增益系數K是根據上一時刻狀態而不斷改變的，因此當場景變化較大時，反而會引入新的誤差。

綜上所述，本文提出了一種基于CHAN 的改進卡爾曼濾波算法。該算法在不同置信區域下選擇不同的增益系數K，避免了上一時刻增益系數的負面影響，提高了定位精度。同時，在判斷置信區域方面，CHAN 算法對NLOS 場景下定位誤差比較敏感，因此選擇其定位結果殘差作為判斷依據，提高了置信區域判別的準確程度。

1 UWB 定位環境及模型

1.1 UWB 室內定位環境介紹

UWB 室內定位系統[17]的節點根據其在無線網絡中的作用和類型分為2 類：第一類是作為坐標系參考的已知節點，稱作錨節點，也可以稱為基站（BS,base station），主要作用是接收目標節點發出的信號并上傳數據；第二類是作為目標節點的標簽，其主要作用是作為待測目標給基站發送信號。

UWB 室內定位系統主要是以各個節點之間發送信號的特征作為測距依據，其定位方程構建算法有基于信號到達角度（AOA,angel of arrival）、基于到達時間（TOA,time of arrival）等。本文采用基于到達時間差（TDOA,time difference of arrival）[18]定位方程構建算法。

在構建定位模型之前，首先要分析UWB 室內定位系統的誤差源，可以分為系統誤差、環境誤差、算法誤差3 類[19]，如圖1 所示。

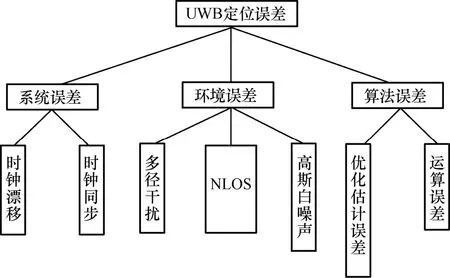
圖1 UWB 定位誤差

UWB 定位系統的兩類系統誤差為時鐘同步誤差和時鐘漂移[20]誤差。時鐘同步誤差是指BS 與Tag設備之間的時鐘并不完全同步，使BS 接收到Tag發送信號時間與真實的信號到達時間不一致，從而降低了定位精度。時鐘漂移誤差是由各個芯片的晶振頻率不同導致的。在實際系統中，可通過時鐘同步處理及調整芯片的晶振頻率降低以上誤差。

環境誤差是實際定位中影響最大的因素，有多徑干擾誤差[21]、NLOS 誤差[22]和高斯白噪聲誤差等。多徑干擾誤差是由信號頻率選擇性衰落引起的，但是UWB 信號具有良好的頻率分辨率，故可以暫時忽略此影響。NLOS 誤差的產生原因是在復雜的室內環境中受到多種障礙物的阻擋，造成了Tag 發射信號不能沿直線傳播到BS，使原本的測量時間延長，降低了定位精度。高斯白噪聲誤差是信號在空間傳播過程中普遍存在的一種誤差。

假設對于某一個BS 而言，Tag 與該BS 之間的情況是隨著時間在LOS 與NLOS 中不斷轉換的。如果不能及時地分辨這2 種信號，并對其進行適當處理，則會導致定位結果誤差增加。為了真實描述室內復雜定位環境，本文假設

其中，PLOS和PNLOS分別為復雜室內定位環境下LOS和NLOS 出現的概率。

算法誤差是定位解算算法在解定位方程時產生的，其大小表征了不同定位算法的性能。

1.2 UWB 室內定位建模

UWB 室內定位系統通常基于不同的測量參數建立不同的室內定位模型。目前，常用的模型有泊松模型、POCA-NAZA 模型、S-V 模型、雙簇模型和IEEE802.15.4a 模型[23]等。其中，IEEE802.15.4a模型是現階段研究最多的模型。因此，本文根據此標準建立室內定位模型。

考慮一個室內定位系統中有N個BS 和一個Tag，其中，BSi= [xi,y i,zi]T是第i個BS 的位置，Tag 與第i個BS 之間的測量距離可表示為[24]

其中，c=3×108m/s 為光速；τi為Tag 信號到達BSi的時間，單位為s；Di為Tag 信號到達BSi的真實距離，單位為cm；n i為滿足N～ (0,)分布的加性白高斯噪聲。

IEEE802.15.4a 的研究結果表明，室內情況下NLOS 誤差的分布滿足Nakagami-m 分布，其均方根時延擴展τRMS和平均超量時延μ有近似1:1 的關系。因此，NLOS 誤差服從指數分布，其概率密度函數為

其中，τRMS可看作滿足對數正態分布的隨機變量。表1 給出了IEEE802.15.4a 中室內住宅和室內辦公室的τRMS，其中，μNLOS和σNLOS分別是τRMS的均值和標準差。

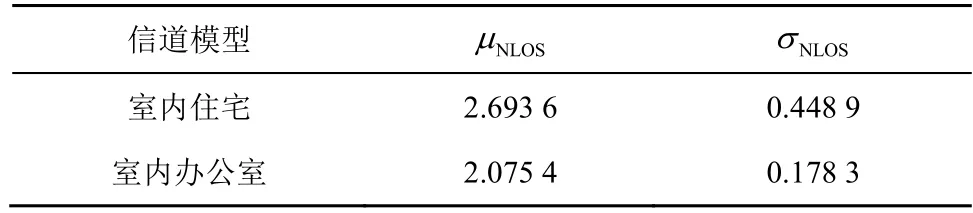
表1 IEEE802.15.4a 中室內住宅和室內辦公室的 τRMS

根據上述情況，在復雜的室內辦公室環境中，UWB 室內定位的距離模型可以建模為

其中，τiNLOS為Tag 到BSi的NLOS 時間，bi為Tag到BSi的NLOS 距離。由于τiNLOS滿足對數正態分布，其值一定為正，即滿足

TDOA 主要依據雙曲線特性實現定位。該算法只需要將BSi進行時間同步，不需要Tag 與BSi之間進行時間同步，更符合實際情況，降低了時間同步造成的誤差。該算法實現的具體步驟為首先將已知的BSi進行時間同步，由Tag 向BSi發射信號，BSi記錄下信號所到達的時間戳，并將其數據上傳給上位機。然后以BSi為基點，用BSj(j≠i)收到信號的時間減去BSi收到信號的時間，就是到達時間差。根據雙曲線的定義，建立N-1 個雙曲線方程，可得到Tag 的具體位置。TDOA 定位算法如圖2 所示。

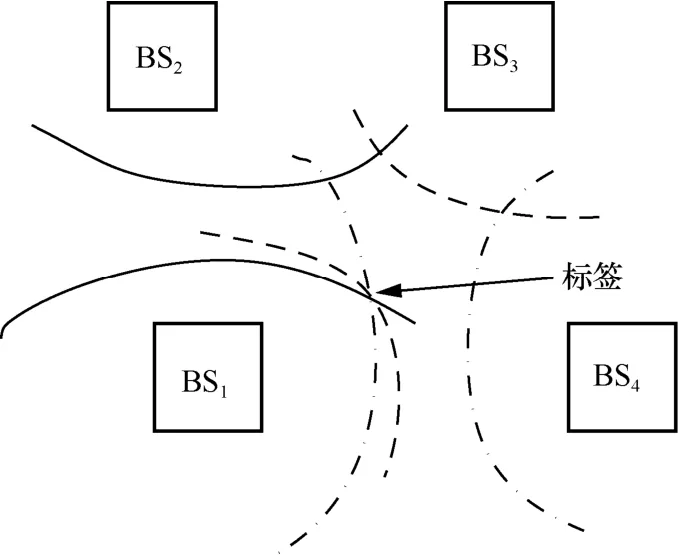
圖2 TDOA 定位算法

圖2 中，BS1、BS2、BS3、B S4分別為4 個已知節點，以BS1為基準畫3 個雙曲線，它們的交點即Tag。假設4 個已知BS 的坐標分別為 (x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4)，Tag 為未知節點，其坐標為(x,y,z)，由上述分析可得

其中，D i表示BSi到Tag 的實際距離，Dj表示BSj到Tag 的實際距離，Dij表示Tag 到BSi的距離和Tag 到BSj的距離的差值，τij表示Tag 發送的信息到達BSi的時間和Tag 發送的信息到達BSj的時間的差值。

將式(8)代入具體數據并化為矩陣形式

可解出Tag 的具體位置為

1.3 基于CHAN 的卡爾曼濾波算法

CHAN 定位解算算法是一種具有閉式解的二步加權最小二乘算法[25]，在噪聲滿足高斯分布的情況下具有較好的算法性能，廣泛應用于各個場景。該算法分為四基站定位與多基站定位，本文采用的是后者。

設Za= [Zp,D1]T為 Tag 未知的位置信息，Zp=[x,y,z]T為Tag 在坐標系中的具體位置，根據式(9)可得

用矩陣Q代替誤差矢量ε的協方差矩陣Ψ，并通過加權最小二乘法求解式(15)可得

其中，Za中的Zp即Tag 具體坐標。上述過程中用協方差矩陣Q代替誤差矢量ε的協方差矩陣Ψ，增加了一定誤差，為了降低這部分誤差的影響，要對上述的過程進行進一步優化，即進行二步加權最小二乘算法的運算

得到的估計結果為

卡爾曼濾波器[26]也被稱為最佳線性濾波器，用于解決狀態估計問題中的線性系統。其主要通過對輸入的預測值和觀測值進行濾波處理，使估計結果更加接近真實值。卡爾曼濾波算法的狀態空間模型為

其中，k為離散時間，X(k) ∈Rn為系統在時刻k的狀態，Y(k) ∈Rm為對應狀態的觀測信號；W(k) ∈Rr為輸入的白噪聲，V(k) ∈Rm為觀測噪聲；Φ為狀態轉移矩陣，Γ為噪聲驅動矩陣，H為觀測矩陣。將CHAN 算法的定位結果作為卡爾曼濾波器的輸入量

狀態一步預測為

狀態更新為

濾波增益矩陣為

一步預測協方差矩陣為

協方差矩陣更新為

其中，P(k|k)和P(k+1|k)分別為對應估計結果的協方差矩陣；R為測量噪聲矩陣；K為卡爾曼濾波增益，是根據協方差矩陣和測量誤差矩陣決定的值，K值越大，代表越相信觀測值，K值越小，代表越相信預測值；(k|k)為上一個狀態的最優估計結果，(k+1|k+1)為當前時間基于CHAN 的卡爾曼濾波的定位結果。

整體而言，卡爾曼濾波是一個不斷迭代并且優化其參數的過程，其最優估計結果越來越逼近真實值。該算法有效地降低了CHAN 算法在NLOS 環境下的誤差。然而，為了保證卡爾曼濾波迭代的準確性，需要在初始位置給一個指定的初值，這個初值必須滿足與標簽的實際位置接近[24]，否則會對后續的迭代過程產生偏移，導致定位結果誤差增大。其次，由于卡爾曼濾波是一連續優化的過程，上一時刻的協方差矩陣影響下一時刻的位置信息。在復雜的室內環境中，存在LOS 與NLOS 信號共存并且頻繁轉換的情況，這使協方差矩陣比較難判斷該時刻的定位信息是否準確，從而導致下一時刻的協方差矩陣受到影響，逐漸產生累計誤差。與此同時，對于一個基站而言，假設LOS 信號與NLOS 信號出現的概率是相等的，會使卡爾曼濾波增益系數K一直維持在0.5 左右，降低了卡爾曼濾波的精度。

2 基于CHAN 的改進卡爾曼濾波算法

為了解決上述問題，考慮到復雜室內場景中LOS/NLOS 場景頻繁切換的特性，對LOS/NLOS 基站存在數目進行置信區域的劃分。同時，考慮到CHAN 算法在NLOS 情況與LOS 情況下定位誤差相差較大，將其作為置信區域的判別依據。最后，根據劃分的不同區域，選擇合適的濾波增益系數K提高定位精度。

對于多基站的定位而言，BS1接收Tag 傳輸的信號是在LOS 場景下，但是BS2接收Tag 傳輸的信號是在NLOS 場景下，這就導致定位環境復雜度的增加。

考慮到CHAN 方法在LOS 基站大于4 個時定位精度較高，將其定位結果和各個基站的位置進行殘差并作為區域判別的置信因子。

假設總共有N個BS，在三維定位中必須有4 個BS 才能解算出Tag 坐標，選取其中任意（l l＞4）個基站為一組，總共有M種組合，其值為

索引集為{Sr,r= 1,2,…,M}。殘差定義為

通過對該測量時刻計算的M組殘差值進行歸一化處理，得到當前測量時刻的置信因子為

其中，α為置信因子，是區域判別指標。同時，對每一測量時刻的M組殘差加權，得到此測量時刻的定位結果為

式(35)是該時刻所有組合殘差加權的過程。殘差值越大，說明定位結果越差；殘差越小，說明定位結果越好。因此，分母為該時刻所有組合情況的殘差值倒數之和，分子為該時刻第r種組合的Tag位置與其殘差倒數之積。考慮到置信因子α表示不同區域內定位結果的可信程度。將定位的區域劃分為3 個，即

其中，Knew為根據不同置信區域選擇的卡爾曼濾波增益，α為置信因子，δ1和δ2為劃分置信區域的閾值。例如，在仿真設置環境中，由多次測量可得出，δ1和δ2的取值分別為0.3 和0.5。在置信區域中，δ1、δ2和濾波增益Knew滿足在可信區域中濾波增益Knew更加相信測量結果，此時α在0 和δ1之間；在模糊區域中，濾波增益Knew會適當地調整測量結果和預測結果的關系，此時α在δ1和δ2之間；在不可信區域中，濾波增益Knew更加相信預測結果，此時α在δ2和1 之間。

根據不同區域選擇不同的卡爾曼濾波增益Knew，并將當前測量時刻的定位結果xTag代入不同的區域進行卡爾曼濾波。

相對于基礎的卡爾曼濾波過程，該過程只更改了狀態更新和協方差更新方程的濾波增益因子

基于CHAN 的改進卡爾曼濾波算法流程如圖3所示。

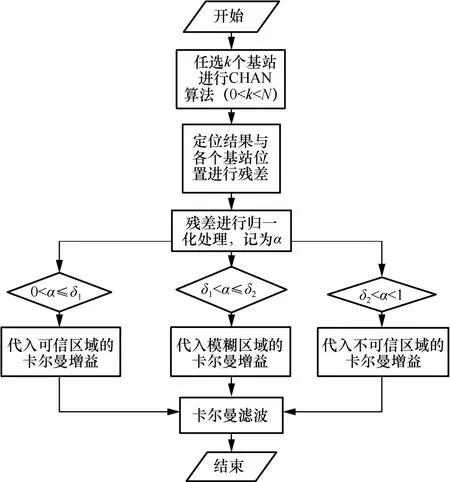
圖3 基于CHAN 的改進卡爾曼濾波算法流程

本文算法解決了卡爾曼濾波在定位初始時定位精度不高和卡爾曼濾波增益K在復雜室內定位場景下產生新誤差的問題，具有不錯的定位精度。

3 實驗與分析

3.1 仿真實驗數據構建

本文實驗主要分析在復雜室內環境下，各種室內定位算法的精度。假設在1 000 cm×1 000 cm×1 000 cm 的復雜室內空間存在8 個BS，其LOS 信號和NLOS 信號的概率都為50%，且為隨機產生。一個物體的運動軌跡為從（200,200,200）到（700,700,700）的勻速直線運動，該物體在每個方向上的加速度都為20 cm/s，由于物體運動時存在一定誤差，其概率分布滿足加性白高斯噪聲，ω的取值為10 cm。因此其真實運動軌跡如圖4 所示。

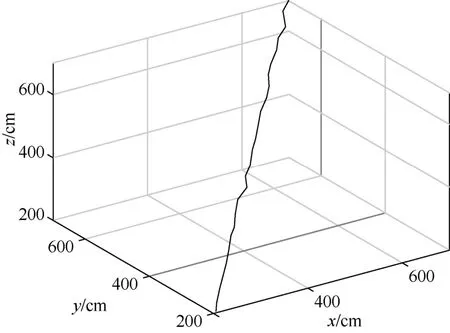
圖4 真實運動軌跡

在UWB 室內定位中，根據IEEE802.15.4a可知，設定測量誤差的標準差符合高斯分布，其均值為0，方差為10 cm；NLOS 的均方根時延擴展τRMS滿足對數正態分布，均值為2.075 4 cm，方差為0.178 3 cm。根據多次數據的測量，閾值δ1=0.3，δ2=0.5。可信區域代表8 個BS 中有5 個及以上BS 的接收信號為LOS 情況，模糊區域代表存在3～4 個BS 的接收信號為LOS 情況，不可信區域代表低于2 個BS 的接收信號為LOS 情況。由于CHAN 算法在5 個基站時就有很高精度，因此本文選取k=5。

綜上，本節構建了一個LOS 信號和NLOS 信號概率相等的復雜室內定位場景，其參數基本符合現實情況。

3.2 仿真實驗數據分析

為了充分說明本文算法的性能，仿真實驗選取3 種相關定位算法與本文算法進行分析對比，分別為傳統的CHAN 算法[8]、基于分組的協同定位算法[15]和CHAN+卡爾曼濾波算法[16]。

圖5～圖8 為傳統的CHAN 算法、協同定位算法、CHAN+卡爾曼濾波算法和CHAN+改進卡爾曼濾波算法的定位示意，運行次數為10 000 次來保證實驗的準確性。圖5 是三維空間內4 種算法的定位結果。從圖5 可以明顯地看出，傳統的CHAN 算法由于室內環境復雜，定位效果很差，運動軌跡偏離真實軌跡較大，甚至出現了先定位點在后定位點之前的情況；基于分組的協同定位算法由于基站分組的非理想化影響，依然存在一定的定位誤差；CHAN+卡爾曼濾波算法由于卡爾曼濾波的加入，一定程度上降低了定位的NLOS 誤差，運動軌跡更加平滑，接近真實運動軌跡。但是由于在初始定位時增益值選取的問題，在運動初始定位的過程中，產生了較大的定位偏移情況；CHAN+改進卡爾曼濾波算法是4 種定位算法中定位誤差最低的算法，其定位軌跡更加接近真實軌跡。同時，在初始定位的過程中，CHAN+改進卡爾曼濾波算法從初始定位時就接近真實的定位軌跡，有較低的定位誤差，相比前3 種算法的定位軌跡有了明顯的校正，解決了卡爾曼濾波在初始位置定位精度不高的問題。綜上，CHAN+改進卡爾曼濾波算法相比另外3 種算法在定位精度和定位穩定性上都有較大提升。

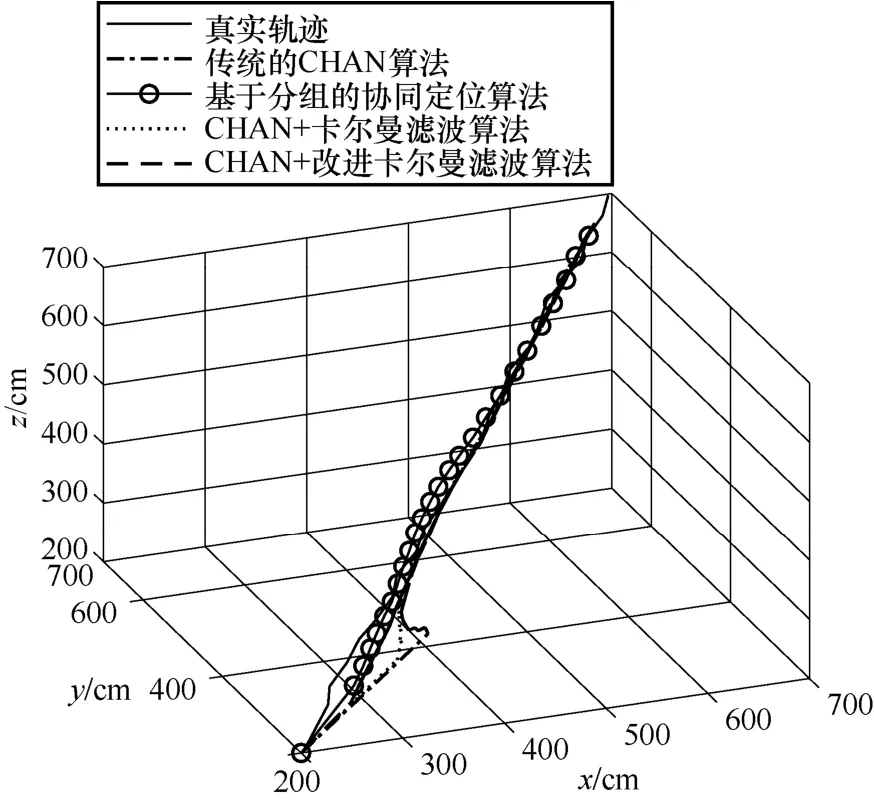
圖5 三維空間內4 種算法的定位結果

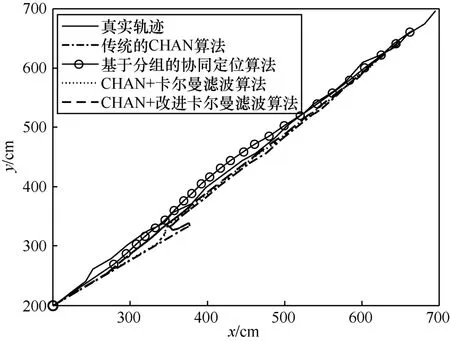
圖6 x-y 運動軌跡

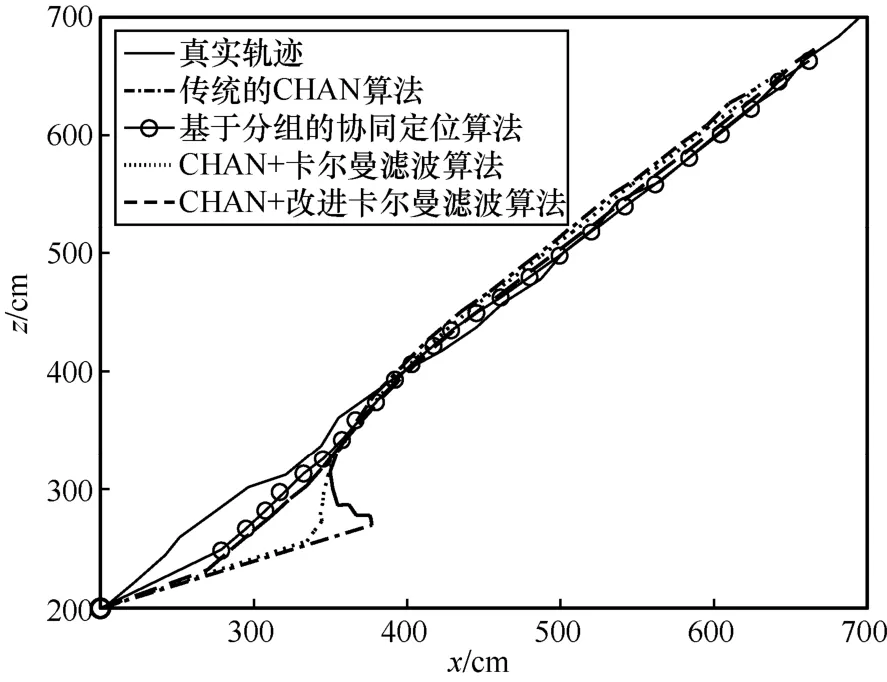
圖7 x-z 運動軌跡

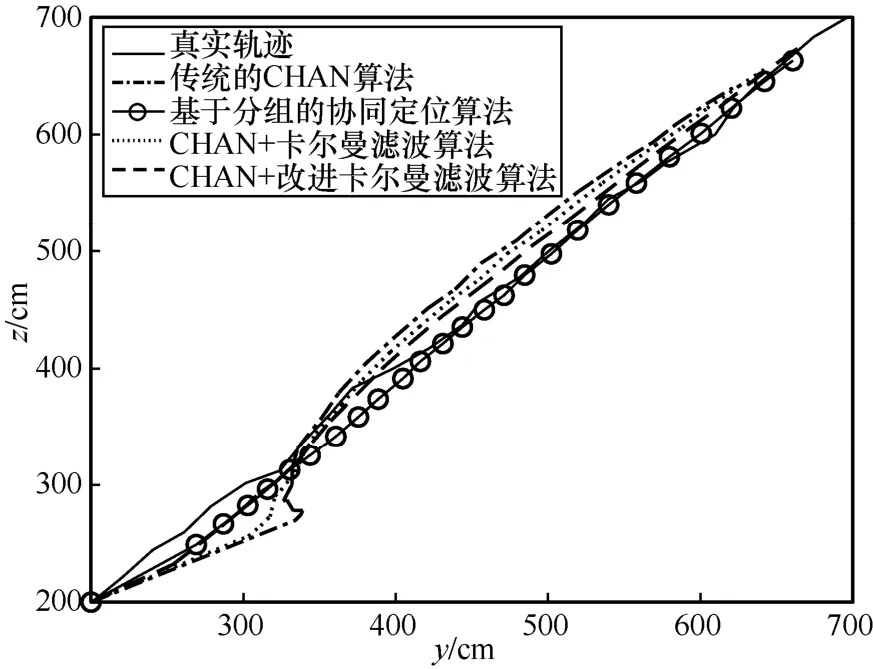
圖8 y-z 運動軌跡

圖9 顯示了4 種室內定位算法的定位誤差。從圖9 可以看出，傳統的CHAN 算法的定位誤差穩定在2.2 m 左右。對于需要精準定位的室內定位來說，傳統的CHAN 算法不滿足其要求。基于分組的協同定位算法受LOS 與NLOS 頻繁轉換和閾值設定的影響，誤差在1.8 m 左右。CHAN+卡爾曼濾波算法的定位誤差在1.0～1.5 m，假設需要定位的運動體是人，則此誤差在人運動的合理范圍之內，可以用于普通的室內定位情況。從圖9 中也可以看出，CHAN+卡爾曼濾波算法在定位初始的位置時誤差仍偏大。CHAN+改進卡爾曼濾波算法的定位精度在0.5～1.0 m，符合室內精準定位的要求，達到了UWB 在民用室內定位中的規范。同時，在定位初始的情況下，也滿足室內精準定位的需求。總體而言，4 種定位算法整體誤差曲線平滑。在整個定位過程中，CHAN+改進卡爾曼濾波算法的定位誤差始終比其他3 種算法定位誤差要小，與傳統的CHAN 算法相比，定位誤差降低了1.5 m；與CHAN+卡爾曼濾波算法相比，定位誤差降低了0.5 m。

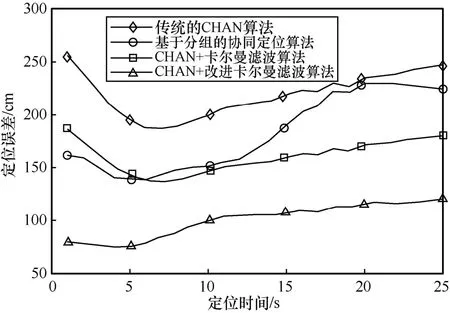
圖9 4 種室內定位算法的定位誤差

為了更好地對比4 種算法的定位精度，表2 給出了在10 000 次定位結果下，4 種定位算法的均方根誤差（RMSE,root mean squared error）。在復雜的室內環境下，傳統的CHAN 算法的RMSE 在2.2 m 以上，有明顯的定位誤差，不能用于室內定位；基于分組的協同定位算法的RMSE 在2.0 m 左右，也存在較大的誤差；CHAN+卡爾曼濾波算法定位精度在1.0 m 以上，基本符合室內定位的需求；CHAN+改進卡爾曼濾波算法的定位精度在0.8 m 左右，與傳統的CHAN算法和CHAN+卡爾曼濾波算法對比，提升了60%和34%，降低了復雜室內環境的定位誤差。

表2 各定位算法的RMSE

同時，在不同定位測量噪聲標準差的場景下，CHAN+改進卡爾曼濾波算法仍然擁有較好的定位精度。如圖10 所示，在固定了LOS/NLOS 基站的分布情況下，隨著定位測量噪聲標準差的增大，各種定位算法的定位精度都在降低，符合實際情況。傳統的CHAN 算法受定位測量噪聲標準差的影響較大，測量噪聲標準差增加的情況下，定位精度降低得十分明顯。基于分組的協同定位算法由于對NLOS 信號進行了簡單的處理，而CHAN+卡爾曼濾波算法和CHAN+改進卡爾曼濾波算則是在卡爾曼濾波迭代過程中，更新質量優劣因子P隨著定位的過程逐漸改善，彌補了測量噪聲標準差的增大。因此，相較于傳統的CHAN 算法，基于分組的協同定位算法、CHAN+卡爾曼濾波算法和CHAN+改進卡爾曼濾波算法受定位測量噪聲標準差的影響較小。在同一測量噪聲標準差的情況下，CHAN+改進卡爾曼濾波算法相比其他3 種算法的RMSE 更小，有更好的定位精度。在定位環境越來越惡劣的情況下，傳統的CHAN 算法的RMSE 趨勢不收斂，定位效果較差。CHAN+卡爾曼濾波算法和CHAN+改進卡爾曼濾波算法的RMSE 逐漸穩定在2.0 m 和1.8 m 左右，對于定位環境十分惡劣的情況而言，在可接受范圍內。

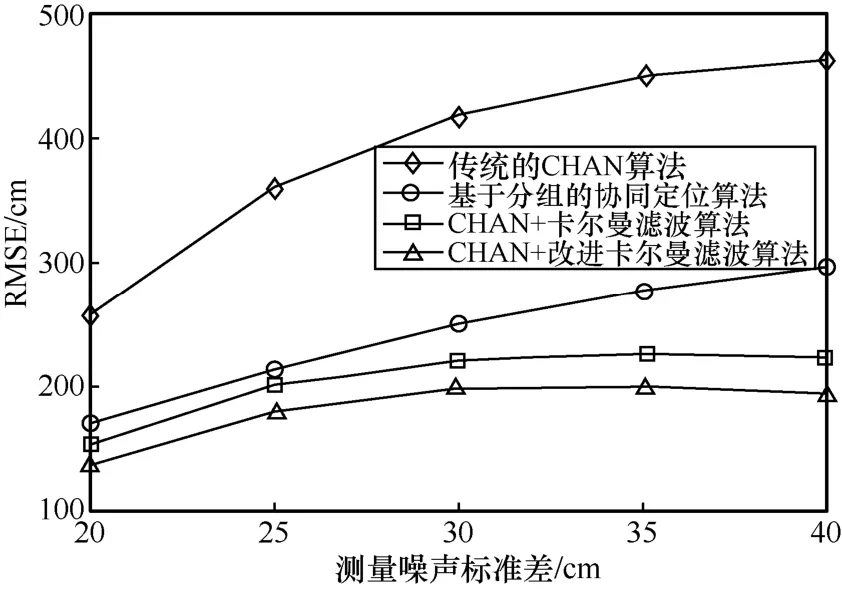
圖10 RMSE 與測量噪聲標準差的關系

本文實驗還驗證了卡爾曼濾波增益系數在初始狀態改善的問題，設ΔK為CHAN+改進卡爾曼濾波算法與CHAN+卡爾曼濾波算法增益系數的差值，其與時間的關系如圖11 所示。從圖11 可以看出，ΔK在初始狀態時接近-0.3，說明CHAN+改進卡爾曼濾波算法與CHAN+卡爾曼濾波算法的增益系數取值有明顯不同，其原因是CHAN+卡爾曼濾波算法在初始定位時濾波增益還未改善。相比CHAN+卡爾曼濾波算法，CHAN+改進卡爾曼濾波算法由于需要對置信區域進行選擇，改善了增益系數，讓其更快地趨于穩定和精準。隨著時間的推移，2 種算法增益系數的差值逐漸縮小，系數逐漸相等，這說明不同區域預先選擇的增益值提高了定位的精度。綜上，CHAN+改進卡爾曼濾波算法在初始狀態時就已經改善了增益系數，降低了由復雜室內環境產生的新誤差。

圖11 ΔK 與運行時間的關系

最后，為了表征不同定位算法之間的復雜度區別，記錄了各種定位算法的實際運行時間，如表3所示。傳統的CHAN 算法的實際運行時間最快，而本文提出的CHAN+改進卡爾曼濾波算法要進行多次CHAN 算法解算，并根據解算結果與各個基站進行殘差，判別置信區域后再進行卡爾曼濾波，增加了算法復雜度，因此實際運行時間最長。但是本文算法實際運行時間仍然滿足定位實時處理的要求，可在實際定位系統中使用。

表3 各種定位算法的實際運行時間

3.3 實際定位環境

根據前文的分析與仿真驗證，本文采用CHAN+改進卡爾曼濾波算法作為定位系統的定位方案。

本文實驗實際環境為某會議室，該會議室長為812 cm，寬為404 cm，高為216 cm，人攜帶UWB定位標簽在選取的范圍內按照指定的軌跡進行移動。8 個定位基站布置如下：主機站坐標為(0,0,25)，其余基站坐標分別為(812,0,25)、(812,404,25)、(0,404,25)、(0,0,216)、(812,0,216)、(812,404,216)、(0,404,216)。在會議室內有明顯的桌椅擺放，隨機遮擋了部分基站與標簽之間的信號LOS 傳播路徑，形成了復雜的室內環境。根據會議室內基站的坐標分布可知，其中位于房間頂部的4 個基站與標簽之間并無障礙物遮擋，此時4 個頂部基站與標簽之間的信號為LOS 傳輸信號；而位于會議室底部的4 個基站與標簽之間存在會議室桌椅的遮擋，該4 個基站與標簽之間的信號為NLOS 傳輸信號，實際測試環境滿足前文假設的LOS 和NLOS 信號分布概率。

3.4 定位數據分析

為了直觀地表現測試的軌跡，本文實驗的標簽運行軌跡為在會議桌上的一條直線，具體的空間坐標為[350,215,40]到[750,215,40]的一條直線，但是由于實際的軌跡并不能嚴格控制為一條直線，因此圖中以黑色的理想預測軌跡作為參考基準，具體定位結果如圖12～圖15 所示。

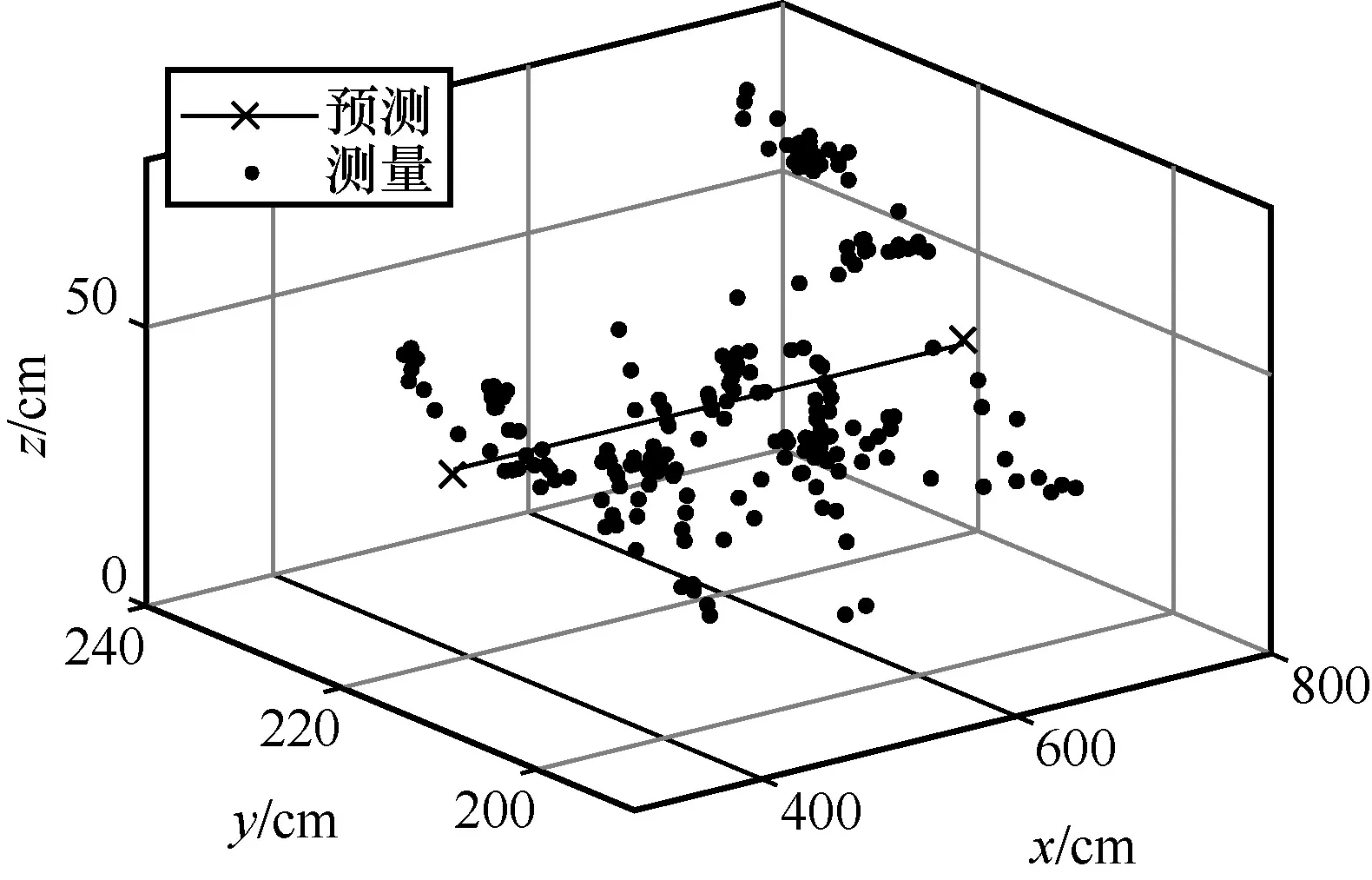
圖12 實際定位軌跡

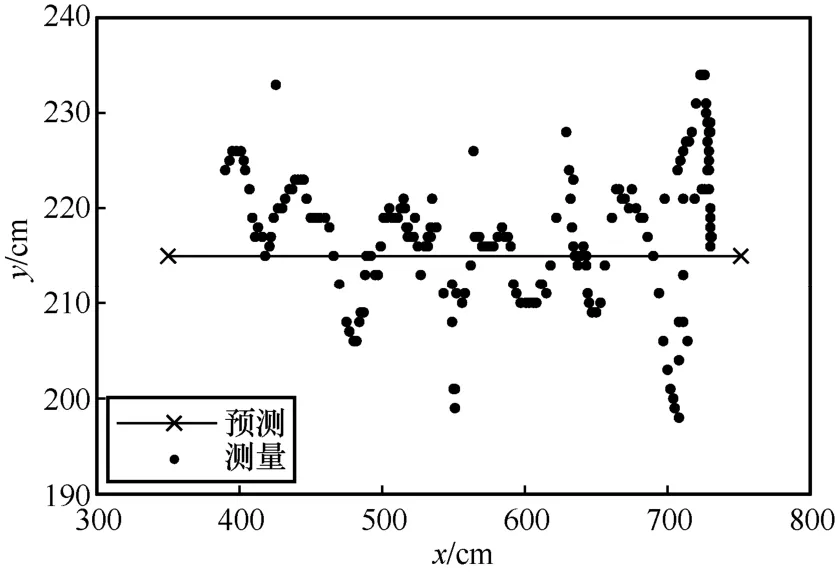
圖13 x-y 實際定位軌跡

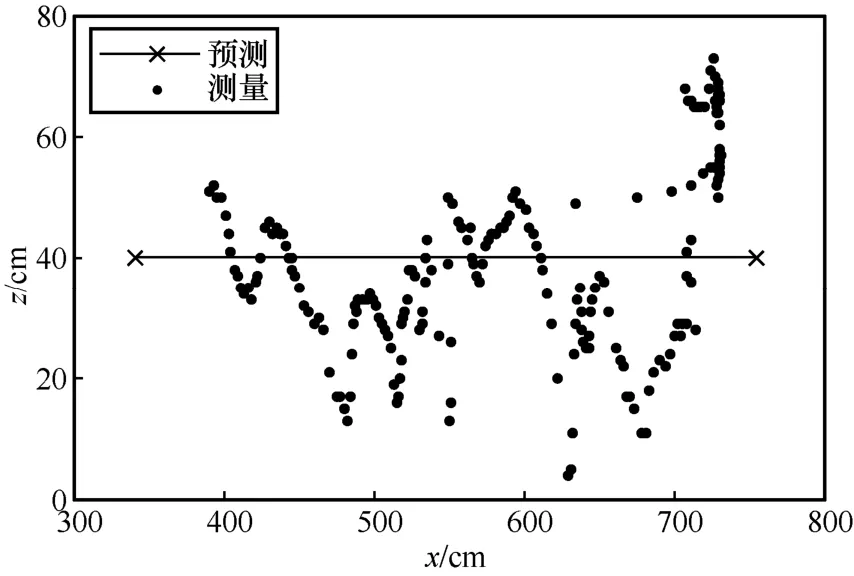
圖14 x-z 實際定位軌跡

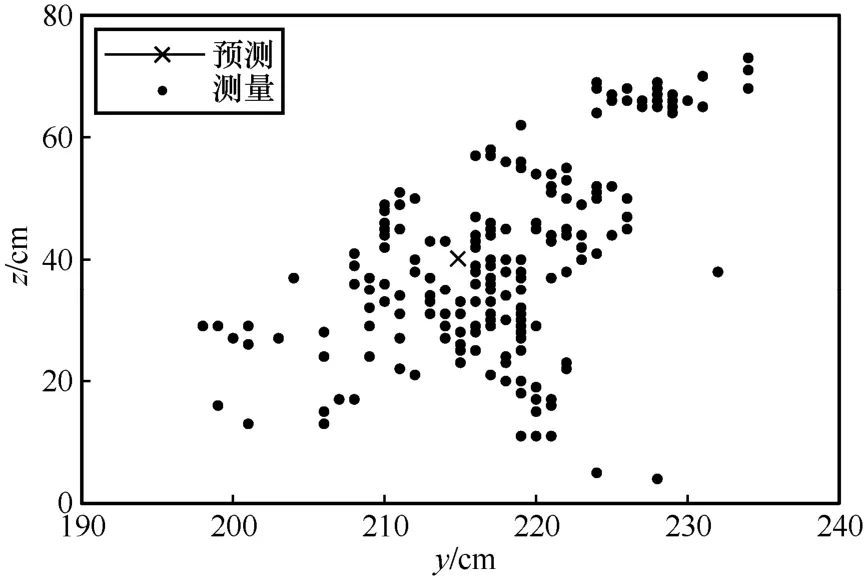
圖15 z-y 實際定位軌跡

根據與理想軌跡的對比可得，本文實驗所用的CHAN+改進卡爾曼濾波算法基本符合預測軌跡，并且在預測軌跡附近波動。由圖13～圖15 可知，y軸和z軸的定位誤差在40 cm 左右，x軸的定位誤差在20 cm 左右。

為了更進一步地說明本文算法相比同類算法的性能優勢，圖16 在給定預測軌跡的情況下，利用實際系統對比本文算法、傳統的CHAN 算法[8]和CHAN+卡爾曼濾波算法[16]的定位結果。從圖16 可知，在初始時刻，由于標簽與基站之間有信號自動校準的時間差，因此初始定位時刻的偏差較大，但是隨著時間的推移，定位結果逐漸穩定。由實際的數據可得，CHAN+改進卡爾曼濾波算法的平均定位誤差最小，在50～60 cm，且其定位的穩定性比其余2 種算法都高。CHAN+卡爾曼濾波算法的平均定位誤差在150 cm 左右，而傳統的CHAN 算法的平均定位誤差在250 cm 左右，并不適用于實際復雜環境的室內定位。上述算法在實際數據中的對比進一步驗證了本文算法的性能。

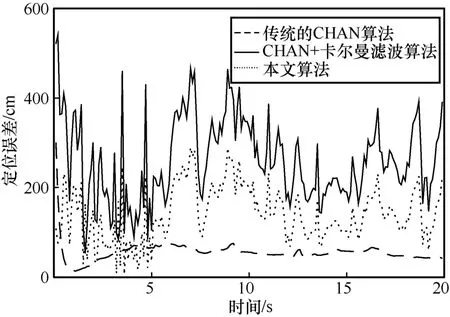
圖16 實際定位誤差

4 結束語

本文提出了一種在復雜室內定位環境下基于CHAN 的改進卡爾曼濾波算法。該算法提高了基于CHAN 的卡爾曼濾波算法在復雜室內環境下的定位精度，并且改善了卡爾曼濾波增益在初始定位時的準確性。通過實際測量驗證，本文算法具有較高的定位精度，在復雜室內環境下精度達到了亞米級，是一種有效的定位方法。