疊層相干衍射成像算法發展綜述*

潘新宇 畢筱雪 董政 耿直 徐晗 張一 董宇輝 張承龍?

1) (中國科學院高能物理研究所,北京同步輻射裝置,北京 100049)

2) (中國科學院大學核科學與技術學院,北京 100049)

3) (中國科學院高能物理研究所,散裂中子源科學中心,東莞 523808)

隨著同步輻射技術的發展和光源相干性的提升,疊層相干衍射成像(ptychography)得到快速發展.疊層相干衍射成像算法解決了傳統相干衍射成像算法收斂速度較慢、容易陷入局部最優解和算法停滯等問題,具有成像視場大、算法魯棒性強、對誤差容忍性高、應用范圍廣等優點,正成為相干衍射成像領域的熱點研究方向.本文首先介紹了疊層相干衍射成像算法提出的背景;然后詳細總結了疊層相干衍射成像算法的發展脈絡、主要的算法流程以及應用場景,并且介紹了疊層相干衍射成像與人工智能結合的新算法及應用潛力;最后介紹了疊層相干衍射成像算法具體的并行化實現及常用軟件包.本文有助于建立疊層相干衍射成像領域算法本身、人工智能以及計算方法全局研究視角,對于促進疊層相干衍射成像方法學的系統發展具有重要的參考意義.

1 引言

傳統的透射成像方法可以記錄樣品的吸收襯度圖像,但是對于弱吸收樣品僅重構樣品的吸收襯度往往效果不佳,需要考慮相位襯度成像.相干衍射成像(coherent diffractive imaging,CDI)可以同時獲得樣品的吸收襯度和相位襯度信息,但其實驗數據僅記錄了衍射強度信息,而丟失了相位信息Φ(x,y).然而,只要樣品尺寸足夠小且入射光滿足相干條件,那么在對衍射圖案進行足夠精細地采樣后,原則上可以恢復出相位信息[1],相位恢復是衍射成像的核心問題.

早在1952 年Sayre[2]就提出CDI 理論最基礎的部分,直至1982 年Bates[1,3]提出相位恢復的過采樣理論,才使CDI 理論趨于成熟.但是CDI 發展初期由于硬件條件導致圖像重構的效果很差,限制了該方法的推廣與發展.1999 年,華人科學家繆健偉[4]在美國國家同步輻射光源(NSLS)上首次成功演示了CDI 成像實驗,自此CDI 技術開始得到快速發展和廣泛應用.1972 年,Gerchberg 和Saxton[5]提出第一個實用的迭代相位恢復算法Gerchberg-Saxton 算法,簡稱G-S 算法.但是該算法需要已知樣品強度圖像,在復空間滿足的相位Φ(x,y)有無數個G-S 算法會出現重建結果不唯一的情況,限制了該算法能應用的場合.在G-S 算法的基礎上,Fienup 于1978 年和1982 年分別提出了混合輸入輸出(hybrid input and output,HIO)算法[6]和誤差遞減 (errorreduce,ER)算法[7].然而,這些CDI 算法存在以下問題,僅利用物域約束和衍射強度的約束將會導致相位重建結果不唯一,即會出現孿生像問題[8];算法往往會因為發散或停滯而無法收斂到全局最小值;同時由于光學技術和工程限制,光斑的大小通常是微米量級,為了滿足相干條件,通常要求樣品尺度小于光斑大小,從而使得成像視場受限.

為了解決上述問題,2004 年Rodenburg[9]和Faulkner[10]提出一種基于全場掃描的無透鏡成像方法疊層相干衍射成像 (ptychography) 方法以及疊層相干衍射成像迭代算法 (ptychographic iterative engine,PIE).它是基于經典的CDI 技術[5,11]發展而來,可以看作是掃描透射X 射線成像 (scanning transmission X-ray microscopy) 以及CDI 技術的結合.Ptychography 算法核心思想是要求相鄰掃描區域有一部分重疊,重疊區域內物體分布函數的一致性構成了額外的約束條件,從而加速相位恢復算法的收斂,確保得到唯一解.運用迭代投影算法解決相位恢復問題理論上可以達到衍射極限精度[12].2007 年,實驗成功驗證了PIE 算法[13],2008 年ptychography 理論進一步成熟[14],實現了光斑和樣品的同時重建功能.相比較傳統的成像方法,ptychography 的優勢在于: 1) 基于掃描的方式不受光斑有限視場的約束,能夠對大尺度樣品進行成像;2) 通過調節聚焦元件和樣品平面位置得到納米至微米量級的光斑,在分辨率范圍上可動態調整并且可以接近衍射極限的分辨率;3) 可以同時重構出探針函數和樣品分布函數,具有較強的數值反演能力和波前重建的功能;4) 對誤差的容忍度較大.因為ptychography 具有這些優勢,其在可見光、X 射線和電子束等不同領域的相位重建和波前檢測[15]均有應用.同時ptychography 與其他光學技術結合,在生物醫學[16,17]、化學[18]、計量學[19]以及超快激光[20]等領域也均有著廣泛的應用.

本文首先介紹ptychography 領域中基本算法,然后總結ptychography 基本算法在實驗效率提升、厚樣品成像和誤差校正等方面遇到的關鍵問題,并介紹優化這些問題過程中ptychography 算法的發展脈絡.特別地,還將介紹ptychography與人工智能結合優化帶來的新方法和新思路.接著總結ptychography 物理算法模型具體的計算機軟件實現,以及海量計算需求帶來的并行化方面的發展,最后展望在未來第四代同步輻射光源HEPS 上的發展前景.

2 Ptychography 算法

2.1 傳統算法概述

Ptychography 最主流的算法是PIE 算法和DM 算法(DM 算法是基于差分圖所設計的算法)[21].2007 年Rodenburg[13]成功完成第一個使用PIE算法的光學實驗后,PIE 算法勢如破竹地進入了成像領域.如圖1 所示,已知入射光束,假設一個待測樣品的初始分布函數為O(r),光束分布函數為P(r-Rj),不考慮樣品厚度,出射光分布函數可以表示為

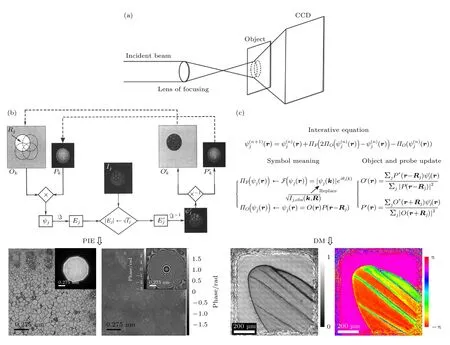
圖1 (a) Ptychography 的基本光路圖;(b) PIE 算法對應的算法流程和重建結果[12];(c) DM 算法對應的算法流程和重建結果[21]Fig.1.(a) Schematic diagram of the basic optical path of ptychography;(b) the corresponding algorithmic flow and reconstruction results of the PIE algorithms[12];(c) the corresponding algorithmic flow and reconstruction results of the DM algorithms[21].

(1)式作為初值參與第一次迭代計算(r,R為空域坐標),迭代過程中首先將出射光變換到頻域中:

然后將探測到的強度值Iobs(k,Rj) 替換之前的強度值,反變換回空域:

再更新樣品和計算誤差:

重復上述流程,直至完成所有位置的迭代.

PIE 算法的核心思想在于使用梯度下降方法(又稱最速下降法)來找到全局最優解.對第n次迭代探測器平面的衍射光做頻域約束后,二者的偏差可以表示為

誤差看作關于不同迭代次數ψ(r) 的函數.對誤差B關于ψ n(r) 進行一階泰勒展開,再考慮理想情況下偏差為0,可得

可以看出(8)式正是梯度下降的形式,詳細推導過程參見文獻[7].

該算法依然存在一些問題,例如需要知道光斑探針分布,對物體的初始化分布函數敏感,不合適的初始化可能會使算法落入局部最優解或導致收斂速度慢、不穩定等.為了優化這一系列問題,Maiden和Rodenburg[22]根據實驗以及數據的特性提出了ePIE 算法.與PIE 算法相比,ePIE 算法具有不同的待測樣品分布函數和光斑波函數的重建更新形式,可以同時解出探針和樣品分布.PIE 算法不僅在初始化上敏感,在具體的實驗操作中,實驗平臺的移動難免會有抖動,光束分布與實際分布的重疊區域有一定的差距,重疊區域的多少會影響PIE算法的收斂性[23].2.2.3 節會詳細介紹實驗誤差帶來的影響以及在算法上如何優化來減小誤差.

DM 算法在2009 年由Thibault 等[21]首次提出.DM 算法是一種非線性優化迭代算法,最早用于解析晶體學中的相位問題[24],如圖1(c)所示.它有效地降低了圖片偽影,提高了圖像重建質量,并且可以同時重建探針和樣品分布函數[10,21].雖然DM 算法不拘束于掃描順序來計算樣品和探針分布函數,但是需要在每一次迭代過程中,計算所有掃描位置的O(r) 和P(r-R) 來進行函數的更新,因此單次迭代的計算量較大.

2.2 傳統算法優化

2.1節介紹的是ptychography 基本算法,但是在實驗過程中依然存在許多問題和挑戰.例如,周期性網格式掃描容易導致偽影,通過引入非周期或非對稱的掃描路線[25](例如螺旋式,同心圓和隨機掃描等) 可降低偽影的影響.此外,針對ptychography 的實驗特點,研究人員發展了許多不同的實驗方法來提高圖像重建速度和成像分辨率等.針對傳統ptychography 掃描完一個區域并且記錄數據后再進行下一位置的掃描,導致實驗效率低的問題,2.2.1 節介紹fly-PIE 算法和單次曝光ptychography算法(single-shot ptychography,SSP).針對傳統算法僅適用于薄樣品而實際樣品厚度在實驗中往往不能忽視的問題,2.2.2 節介紹厚樣品成像算法3PIE.針對ptychography 實驗結果對掃描位置的準確性和探針的相干模態敏感、實驗誤差等問題.2.2.3 節介紹面向位置和相干模態的優化算法.

2.2.1 效率優化算法

2.2.1.1 fly-PIE 算法

Ptychography 實驗過程中需要對每一個離散掃描區域進行步進掃描,每掃描一塊區域電機將會反復經歷啟動-停止過程,帶來無意義的時間消耗.2014 年Clark 等[26]理論上證明了連續掃描和步進掃描采集到的圖像重建后的效果相當,為提高掃描效率提供了理論基礎,進而提出fly-PIE 算法.其算法思想是將探測器采集時間設為T,選擇足夠小的時間步長 Δt,將探測器采集時間分為n個區域,以恒定速度v掃過的小區域vΔt作為一個數據模態,不同數據模態求和后的值為探測器所采集的衍射強度值.第j個位置的衍射強度等于掃描時間T內強度的疊加:

其中,掃描時間T=t2-t1恒定不變,P z表示旁軸傳播,P(r) 表 示探針函數,O(r+rj+vt) 表示第j個位置飛掃后的待測樣品函數.如果選擇一個小的時間區域則可以對(9)式做離散化處理:

每個模態代表一種完全相干的衍射模式,但不同模態之間非相干,其強度相加是一種非相干疊加,可較好地描述光或樣品的部分相干狀態.在部分相干疊加下的相干狀態與完全相干疊加(傳統ptychography)的效果持平,前者甚至更好.

2.2.1.2 SSP 算法

fly-PIE 算法雖然通過飛掃替換步進掃描縮短了電機移動的時間,提高了實驗效率,但是依然存在以下問題.一方面,由于每個掃描位置需要足夠的曝光時間獲取衍射信號,電機移動的物理速度是有上限的,依然存在電機移動時間浪費.另一方面,電機快速移動中的抖動會產生光斑位置偏差,電機移動越快,出現光斑偏差的概率越大,進而導致重建的探針分布函數出現錯誤.2013 年中國科學院上海光學精密機械研究所潘興臣等[27]提出了SSP算法.該算法避免了通過電機移動掃描樣品,由于無需電機移動樣品,也無需考慮光斑位置誤差,可以一次性掃描大范圍的樣品面積使得實驗效率大大提高.實驗示意圖如圖2 所示,算法思想為一束相干光經過準直照射到網格光柵后發生衍射,網格光柵會使入射光發生分離.根據光柵的規格不同,照射在樣品表面的光探針數量不同.通過設置光柵與樣品的距離使相鄰的光探針在樣品表面有一定的重疊.在不放置測試樣品的情況下,可以測得入射光通過網格光柵后的圖樣.通過相位恢復算法或傳統的PIE 可以得到精確的入射光分布函數.根據光柵的間距以及物函數G(x,y) 可以給探測器端所記錄的各個衍射圖案進行標號 (m,n) .不同標號的光斑表示為

圖2 (a) fly-PIE 的原理示意圖[26];(b) SSP 算法原理示意圖[27];(c) fly-PIE 算法單模態和多模態的重建圖像對比;(d) SSP 實驗對強散射樣品和蜜蜂翅膀的光斑、模量和相位結果Fig.2.(a) Diagram of fly-PIE[26];(b) diagram of SSP[27];(c) comparison of reconstructed images of fly-PIE algorithm using single and multi-modal;(d) probe,modulus,and phase results of the SSP experiment for stronger scattered samples and the bee wings.

(11)式對應于照射至樣品表面的光斑探針,同時可作為圖像重建的入射光探針函數.

2016 年Sidorenko 和Cohen[28]進一步改進了SSP 算法.他們基于4f成像系統(由兩塊透鏡同軸共焦組成,物平面與像平面距離大于等于4 倍焦距)將網格光柵換為微孔陣列來進行分光,有效地提升了成像效果.由于物體同時被多個重疊探針照射,CCD 端的強度表示為

其中,角標m是微孔陣列標號,k m為相應微孔分光的波矢.由于(12)式求和號可以放在絕對值外,因此可以對第m個探針的單個模式應用傳統的PIE 算法或是 ePIE 算法進行重建.但是因為總的強度是求和的,所有光束的多個衍射圖案實際上會相互干擾.因此,當使用區塊中的衍射圖案進行重建時,來自其他針孔的光束對衍射圖案的貢獻被視為噪音.為此,Sidorenko 和Cohen[28]計算了微孔數造成的噪聲極限,以此更改焦距、物距等光學系統參數,減小噪聲的影響.同時他們還改進了 SSP實驗不同孔徑構型,可能會提高算法的收斂速度.對于噪聲減小的優化方案,嘗試不同的微孔形狀或許會減少噪聲的影響從而提高魯棒性.2018 年,Chen 等[29]提出了多路復用的SSP 實驗技術,不僅能重建探測光束的振幅和相位,還能恢復其偏振態.目前,SSP 算法已經運用到了多個領域,例如光學編碼[30]和加密系統[31,32]等.

雖然fly-PIE 和SSP 兩種算法分別從時間和空間上提高了算法效率,但這兩種實驗算法本身仍然存在缺陷.fly-PIE 的問題在于如何確定部分相干模態的數量,而且使用部分相干模態相加會導致強度降低.SSP 技術的局限性在于: 1) 分束的衍射信號均由一個探測器同時采集,衍射信號的空間頻率范圍將非常有限,不同的高頻衍射信號會有一定弱干涉,無法獲得高分辨率圖像信息;2) 實際應用中分光光柵的制作成本相對較高.改進后的SSP雖然使用了不同的光柵構型,但是噪聲問題變得更加嚴重.如何降低SSP 噪聲以及不同光柵構型對噪聲的影響是后續發展的優化方向.

提高成像效率的算法還有傅里葉疊層顯微鏡成像(Fourier ptychographic microscopy,FPM).FPM 是一種合成孔徑技術,能夠在非相干光實驗條件下重建圖像.由于篇幅限制不在此詳述,讀者可閱讀相關文獻[33-36].

2.2.2 厚樣品成像算法

Ptychography 實驗技術一般適用于薄樣品衍射成像,厚樣品容易出現探測器信號缺失,重建圖像不準確等問題.但這樣就限制了ptychography的應用范圍.Maiden 等[37]提出了一種新的算法,可以重建厚樣品,稱為3PIE 算法.他們在圖像重建中將樣品切片,對每一片進行重建,然后再按照傳播順序一層一層地恢復,如圖3 所示.下面給出3PIE 算法的具體流程.

圖3 (a) 3PIE 算法的示意圖[37];(b) 使用 3D-ptychography 技術對部分紙張組織的圖像采集結果[37] (圖(b)前兩幅是上層組織的模量和相位,后兩幅是下層組織的模量和相位)Fig.3.(a) Schematic diagram of the 3PIE algorithm[37];(b) the result of image acquisition of some paper tissues using the 3Dptychography technique[37] (The first two pictures shows the modulus and phase of the upper tissue,and the last two shows the modulus and phase of the lower tissue in Fig.(b)).

1) 確定所需重建的圖像數據,標記其強度為Ic(u),初始化探針函數和樣品中每層切片的分布函數.

2)計算第一層的出射波前

其中,Rc是掃描路徑.

3)將第一層出射波前傳播至下一層,作為下一層的入射波前

4)計算第二層的出射波前

同樣再將其傳播至第三層作為入射波前

5)如此計算直至最后一層出射波前ψe,N(r) .

6)使用傅里葉變換或菲涅耳衍射傳播至探測器,得到頻域空間的理論值

7)用實際探測得到的強度值替代理論計算得到的強度,

8)再將其進行反向傳播,得到第N層切片的修正估計值:

設置更新函數:

9)更新第N層切片入射波函數和樣品分布函數,

10) 再反向傳播至上一層切片,得到上一層修正的出射波:

11) 重復步驟9)和步驟10),計算每一層切片,直到第一層切片的波前.

12) 更新波前探針函數和樣品分布函數,

13) 將每層的樣品分布和探針更新:

并將其作為下一次迭代的初值.

14) 重復上述步驟1)—13),直到滿足終止條件或達到固定迭代次數.

此外,3PIE 算法要求在掃描期間待測樣品不能發生變化,入射光探針的狀態穩定,收集的強度數據集輸入模型時與相應切片傳播的測量衍射圖案相匹配.3PIE 算法繼承了PIE 算法的易理解性.但是由于對樣品進行切片操作,同時還有掃描曝光操作,無疑會對計算量和計算速度提出挑戰.切片數量的多少會直接影響重建的效果以及計算效率.但是在噪聲方面,切片操作會讓噪聲的權重降低從而提高圖片重建的質量.

2020 年,Barutcu 等[38]提出了一種與梯度下降算法結合的Ptycho-Tomography 算法,避免了厚樣品重建中不同層之間的偽影問題.在材料領域[39-41],3D ptychography 算法可以重建出更多的細節而被廣泛應用.3D-ptychography 算法還與SSP 算法相結合[42],在近軸向對厚樣品照明具有明顯的抗干擾性和良好的圖像重建質量.

2.2.3 誤差校正算法

通過前文對PIE 算法的簡要概述可以看出迭代算法通常需要探針位置足夠精確,否則需要能夠設計出可以自動修正探針位置的算法.上述算法需要光斑及相關參數嚴格滿足兩點: 一是掃描過程中位置足夠精確;二是函數參數設置足夠確定或位置參數個數不能超過一定數量[43].電機的移動、輻射的熱效應、光源的變化、地面的微振動等因素影響會對高分辨納米成像實驗產生嚴重影響.例如,光斑抖動會造成樣品曝光時間內,光斑呈現模態不唯一的情況(光源的輻射場發生改變,相應的相干模式也會發生變化);輻射的熱效應也會使樣品內部發生改變,不再是靜態混合;此外,同步輻射裝置中的振動、鏡子的熱變形或是缺陷、樣品的偏移等都會使理論掃描位置和實際掃描位置出現誤差.下文主要介紹多模態條件下優化位置誤差和修正參數不確定性的算法.

2.2.3.1 多模態優化算法

多模態可以理解為一束光中不相同的相位、模量信息的疊加,導致光是部分相干.早在1998 年Nugent 研究小組[44]明確定義了部分相干光場.他們用平均坡印廷矢量定義光場,并且結合連續性方程推導出部分相干光的相位表達和恢復方程.而后在2009 年Nugent 研究小組[45,46]基于迭代算法將部分相干光進行模式分解,從而達到信息的均勻與恢復.如圖4(a)所示,多模態產生原因主要有三點[47]:1) 光源本身的輻射,內部有一定的退相干以及光源的振動導致的部分相干;2) 樣品內部發生量子態的混合和平穩隨機過程;3) 探測器的點擴散特性所導致的衍射信號模糊,形成另一種退相干機制.

圖4 (a) 多模態產生原因的示意圖和多模態重建圖[47] (其中模糊的圖片為單模態重建，下方為探針的 5 個主要模態);(b) 單層WS2 樣品在不同電子劑量條件下單模態和多模態的重建圖像[49];(c),(d) 分別使用OPRP 算法和ePIE 算法的重建結果和探針的4 個主要模態占比[48]Fig.4.(a) Schematic diagram of the causes of multimodal generation and the multimodal reconstruction[47] (The blurred image is the unimodal reconstruction,and the 5 main modes of the probe are shown below);(b) the reconstructed images of unimodal and multimodal reconstructions of the monolayer WS2 sample under different electron dose conditions[49];(c),(d) the reconstruction results using OPRP algorithm and ePIE algorithm respectively and the four major mode occupancies of the probe[48].

因為在實驗中存在掃描過程,掃描過程的各種振動使得光線的模態發生改變(位置和波前等因素)從而導致退相干效應.并且因為需要移動平臺且每一步的移動可能會有些許誤差,導致重疊區域發生變化.而且大型同步輻射裝置使用的 X 射線輻射有些許不同,在考慮輻射效應下,有些樣品的結構或許會發生改變.以上所有因素疊加會導致整個實驗出現多模態情況.如果將每一次掃描位置中的模態視為一個系統整體,不同模態之間是非相干疊加.這樣最后的圖像重建便是所有不同模態重建出的圖像的非相干疊加.

假設有m=1,2,···,M個模態產生,不同模態集合可以記作

與 PIE 算法基本相同,其算法如下.

1) 計算第j個掃描位置M個模態的傳播函數

其中下標k代表迭代次數.

2)傅里葉變換后傳播至探測器,計算誤差函數

3) 對不同模態傳播函數的振幅進行加權修正:

4) 進行傅里葉反演至空域.

5) 修正物體和探針:

6) 順次改變掃描位置,重復上述步驟1)—5),完成第k次迭代.得到M個探針和樣品函數,并計算每個像素的平均誤差:

7)其中,X和Y代表探測面積.

8)上述計算值作為下一次迭代的初值,迭代計算直至誤差最小.

多模態的產生是不可避免的,但總體可將其分解成多個部分相干光的疊加.2016 年Odstrcil 等[48]提出了OPRP 算法(orthogonal probe relaxation ptychography).他們利用奇異值分解,將探針分解成多個模式,得到了不錯的圖像重建結果.Chen[49]在2020 年使用多模態探針重建了納米結構材料的原子結構,并且與單一模態實驗結果對比發現在追求高分辨率、高精度和大視場成像時多模態重建的重要性.同時多模態相比傳統的算法會產生更大的數據量.為了提高圖像重建的效率,需要采用GPU 并行加速.PyNX[50],Ptypy[51]和Ptychopy[52]等軟件均支持GPU 并行處理圖像數據,提高重建效率.

2.2.3.2 位置精度誤差修正算法

上文提到ptychography 實驗中光斑探針位置會對圖像重建有明顯的影響.Rodenburg 等[43]指出探針傾斜、漂移和位置隨機誤差都會對圖像重建質量有影響.在TEM-ptychography 上進行了一系列的模擬實驗,結果如圖5 所示.探針位置的變化不僅僅會使圖像重建的質量下降,而且如果數據集整體發生位置偏移,會使得其自身是自洽的,但是重建出的圖像整體會有一定的錯誤,從而誤導我們對圖像的分析.因此非常有必要修正光斑位置誤差.未來第四代同步輻射光源HEPS(high energy photon source)上,高相干性光源會降低多模態的影響,但由于各種振動,工程設計和光學元件產生的位置誤差是無法避免的.如何設計出更高效,更準確的位置誤差算法是未來提高圖像重建質量的重要方向之一.

圖5 位置誤差對圖像重建質量影響示意圖[43] (a) 對應圖(b)—(e)的探針位置;(b) 隨機位置誤差重建的結果;(c) 探針逆時針傾斜重建的結果;(d) 探針漂移重建的結果;(e) 探針位置在垂直方向上有擴展的重建結果Fig.5.Diagram of the effect of position error on image reconstruction quality[43]: (a) Probe positions in Fig.(b)—(e);(b) result of the random position error reconstruction;(c) result of counterclockwise tilt of the probe reconstruction;(d) result of the probe drift reconstruction;(e) result of the reconstruction of the probe position with extension in the vertical direction.

退火算法[53]的具體流程和ePIE 算法基本類似,除了在樣品和探針迭代修正方程中添加了對位置誤差的修正.退火算法主要目的是修正探針位置的平移、偏移、傾斜、漂移以及隨機位置誤差的產生.退火算法的示意圖如圖6 所示,藍色小圓圈代表應測位置,藍色矩形代表實測位置,虛線圓圈代表產生隨機位置誤差.

首先引入修正向量C j,以及沒有隨機位置誤差的傳播函數

然后設置m=1,2,···,M個隨機位置誤差r0(k)Δm,其中r0(k) 的取值隨迭代的次數線性減小.Δm=[δx,m,δy,m],隨機位置誤差向量的取值在±1 之間.含有隨機位置誤差的傳播函數為

與ePIE 不同的是,需要選擇出與真實情況最為接近的傳播函數作為算法的迭代函數,做法如下.

1)將ψ0和ψ m做傅里葉變換Ψ m(u)=Fψm得到探測器上的被估計值Ij(u) (u為倒易空間坐標).

2)計算實際探測與估計值的誤差:

3)選取誤差結果最小的傳播函數作為迭代算法中的反向傳播波函數,記作Ψ n(u) .

4)將探測的振幅值替代理論估計值,得到反向傳播后的出射波函數:

5)更新位置修正向量

6)更新樣品分布函數:

7)更新探針函數

重復上述步驟直到所有掃描位置均完成迭代.

之后,Maiden 等[53]提出可以修正全局位置誤差的算法,稱為e-pcPIE.其算法思想是額外考慮以下誤差: 探測器平面相對樣品平面的旋轉、樣品和探測器距離測量的不準確造成縮放比例的誤差,以及數據獲取過程中的線性漂移誤差.與上述方法一致,只是將修正向量加入關于旋轉和距離的誤差向量和標量,每次迭代更新時用隨機小量更新迭代,重建后的圖像質量顯著提升.

2.2.3.3 相關匹配算法

相關匹配算法(serial cross-correlation)[54]在交叉相關算法[55](cross-correlation)基礎上演化而來.由于前后兩個掃描位置的重疊具有一定的關聯性,相關匹配算法的核心思想是運用互相關函數求極值,得到兩次迭代過程中樣品分布函數修正的位置誤差,從而對每一次迭代中的位置進行修正，如圖7 所示.與ePIE 算法的具體迭代過程類似,相關匹配算法在更新樣品分布函數后對其位置進行更新修正.樣品分布函數宗量為實域r和位置誤差修正R j,m,角標j代表掃描位置,m代表迭代次數.根據相關函數

圖7 (a),(b) 在每一個掃描位置x 和y 方向的位置誤差[54];(c),(d) 使用可見光的X 射線重建樣品圖像結果[54];(e)—(h) 使用調制器的X 射線重建樣品圖像結果[54];(i)，(j) 使用KB 鏡的X 射線重建樣品圖像結果[54].其中圖(c),(e),(g),(i)是使用相關匹配算法優化的結果，圖(d),(f),(h),(j)是未使用相關匹配算法優化的結果Fig.7.(a),(b) Position errors in the x and y directions at each scan position[54];(c),(d) X-ray reconstructed sample image results using visible light[54];(e)—(h) X-ray reconstructed sample image results using modulator[54];(i),(j) X-ray reconstructed sample image using KB mirror[54].Fig.(c),(e),(g),(i) and Fig.(d),(f),(h),(j) are the results optimized with and without using the corss-correlation algorithm,respectively.

對其求極值可以得到位置誤差修正值C j,m.將下一次迭代的位置誤差修正為

參數κ是一個常數或是隨迭代次數減小的線性量.函數Λ m(r) 代表光斑函數,選擇對樣品探測貢獻最大的區域.將修正后的宗量帶入樣品或探針函數后進行重構即可.

位置誤差對相位項的影響較大,相關匹配算法解決的是平移誤差所帶來的相位影響.相關匹配算法是運用圖像處理領域中自相關系數的思想實現的一種算法.將前后兩次的迭代過程整體視為一張具有相互關聯性的圖像,從而找到其中最大關聯,進而修正位置誤差.

2.3 Ptychography 與人工智能

近年來人工智能在圖像處理領域取得了很多不錯的成績,例如圖像識別、閾值分割、目標檢測、去噪和超分辨恢復等.國際上各個國家也在大力發展人工智能領域在基礎科學等實際應用方面的價值.美國在過去5 年資助資金達14.24 億美元多[56].圖像處理與光學有密不可分的關系,科學家們希望利用人工智能在圖像處理上的準確性、魯棒性、泛化性以及提升效率等優勢,對光學領域的發展做出推動.并且人工智能的深度學習領域適合解決多種任務模式相混合、任務復雜等問題.復雜問題的解往往是在高維空間，而傳統的計算方式幾乎不可能完成.由此催生了AI for Science 這一科學范式.人工智能可以賦予科學家更高效、更強大、更準確的計算推理能力,將人工智能作為工具在科學領域使用將成為主流.Ptychography 作為光學領域分支,不僅有物理建模過程還有后續的圖像處理需求.盡管傳統ptychography 及其優化算法在不同應用場景下均取得了不錯的圖像重建效果,但是對于多種實驗誤差相互耦合的情形,傳統算法將束手無策.機器學習、深度學習等人工智能算法,可一次性完成多種任務的處理,適合處理復雜任務相互耦合的情形.基于人工智能的ptychography 圖像重建方法逐漸成為研究熱點.

2017 年Maiden 等[57]基于機器學習中的動量梯度下降算法思想提出了mPIE,經過一定次數迭代后在待測物體的分布函數更新公式中添加動量項使得算法的迭代次數大量降低,收斂速度顯著加快.同年,Kappeler 等[58]首次提出基于卷積神經網絡 (CNN)對傅里葉疊層成像 (Fourier ptychography,FP)的圖像進行重建.Kappeler 搭建了PtychNet,其架構如圖8 所示,包含3 個卷積層,其中第1 層是64 核9×9 的卷積層,第2 層是32 核5×5 的卷積層,最后通過ReLU(linear rectification function,ReLU) 激活函數全連接.在掃描位置無重疊和有重疊兩種情形下,與迭代誤差下降（iterative error reduction algorithm,IERA）算法[59]重建進行對比,PtychNet 在沒有重疊的條件下與IERA 算法持平,但是重疊率大于50%的情況下圖像重建的信噪比略低.不過PtychNet 的計算速度卻快于IERA 算法,并且在低迭代次數的情況下,PtychNet 重建的圖像的信噪比高于IERA 算法.而后FP 與機器學習方法結合,也提出了其他不同的網絡構造[60,61],同樣有很好的圖像重建效果.Ptychography 領域的工作逐漸發展起來.

圖8 PtychNet 網絡架構示意圖和重建圖像結果[58] (a),(b) 掃描無重疊的圖像重建;(c),(d) 掃描有重疊的圖像重建Fig.8.Schematic of the PtychNet network architecture and reconstructed image results[58]: (a),(b) The image reconstruction with no overlap of scans;(c),(d) the image reconstruction with overlapping scans.

探測器的本底噪聲和光源所帶來的泊松噪聲在實驗中一般不可忽略.噪聲導致迭代算法重構出的圖像質量會變差.Metzler 等[62]在2018 年結合正則化去噪（regularization by denoising）[63]以及DnCNN 網絡[64]構造出prDeep 網絡.因為其構造形式使得prDeep 可以應用于相位恢復和去噪等各種問題領域.圖像偽影問題在重建算法里也很常見,2019 年I??l 等[65]通過結合深度神經網絡（DNN）和 HIO 算法構建了新的相位恢復網絡.他們將DNN 網絡嵌入HIO 的迭代過程中，每一次迭代過程中用DNN 網絡去除圖像偽影,DNN 網絡中的卷積自帶部分去噪和分辨率恢復的能力,最后再用一次DNN 網絡進一步恢復高分辨圖像,效果顯著.

Cherukara 等[66]構造了網絡PtychoNN,可以基于光源數據同時重建出振幅和相位信息.如圖9所示,與傳統的ePIE 算法進行對比,發現稀疏采樣條件下,PtychoNN 表現出比ePIE 更好的圖像重建效果.這意味著重建圖像時不一定需要完全滿足重疊面積50%以上,可以適當放寬條件.重疊條件的放寬意味著光源振動、探測器振動等因素導致的位置誤差和多模態也可以忽略.他們還指出稀疏采樣使得采樣點密度減少,使得特定分辨率成像的輻射劑量降低.

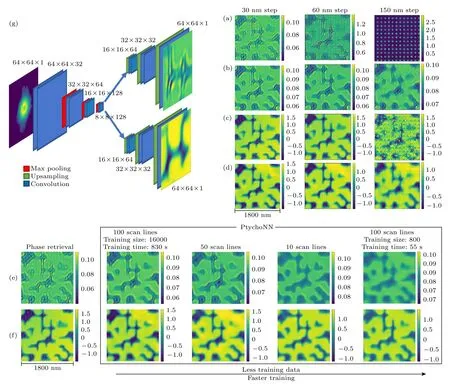
圖9 (a)—(d) PtychoNN 與ePIE 重建的結果對比[66] (a),(c) 使用ePIE 算法重建的結果;(b),(d) 使用PtychoNN 重建的結果.(e),(f) PtychoNN 在少量數據集上的重建質量的對比,發現在至少800 個數據集上可以得到合理結果;(g) PtychoNN 網絡的結構Fig.9.The left figure above shows and the right figure shows the comparison of the results of the reconstruction of PtychoNN and ePIE[66]: (a),(c) The results of the reconstruction using the ePIE algorithm;(b),(d) the results of the reconstruction using PtychoNN.(e),(f) Comparison the reconstruction quality of PtychoNN on a small number of datasets,and find that reasonable results can be obtained on at least 800 datasets;(g) structure of the PtychoNN network.

語音信號處理領域同樣存在相位恢復問題.對ptychography 成像技術與語音信號處理中短時傅里葉變換(short-time Fourier transform,STFT)的相似性進行分析后,Welker 等[67]在2022 年提出了深度迭代投影(deep iterative projections,DIP)神經網絡算法(圖10).對音頻信號做STFT 后，使用幅度譜還原信號但丟失相位信息.他們在語音相位檢索DeGLI (deep Griffin-Lim iteration)架構的基礎上優化ptychography 算法,將交替投影(alternative projection,AP)算法的輸出結果作為DNN 網絡的輸入,DNN 旁支對其進行結果的預測并且與AP 算法的結果相結合后作為下一輪迭代的輸入.他們還通過模擬比較了將DIP 網絡作為初始迭代步驟,然后轉用DM 算法進行迭代和只使用DM 算法兩種實驗結果,發現DIP 網絡作為初始重建步驟在低迭代輪次下的收斂速度優于僅使用DM 算法.同時他們還比較了相同的誤差閾值下,不同算法達到閾值的迭代次數和時間.結果也表明DIP 算法要優于傳統的相位恢復算法.神經網絡的優勢在于更快的圖像重建速度和低迭代次數圖像的精度比傳統算法收斂結果更好.

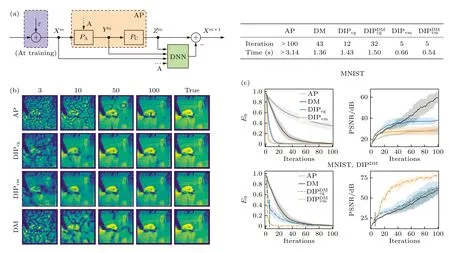
圖10 (a) DIP 網絡的結構示意圖;(b) 使用DIP 網絡、DM 算法與AP 算法重建圖像結果的對比[67],其中DIPcg 和DIPvm 指兩種不同模式的DIP 網絡.右上方表格為誤差閾值為0.1 的情況下各個算法需要的迭代次數和時間,可以看到DIP 網絡表現很好.(c) DIP 網絡運用到MINST 庫上的測試結果Fig.10.(a) Schematic diagram of the structure of DIP network;(b) the comparison of the reconstructed image results using DIP network,DM algorithm and AP algorithm in reconstructed image results[67],where DIPcg and DIPvm refer to two different modes of DIP networks.The table on the top right shows the number of iterations and time required by each algorithm for an error threshold of 0.1,and we can see that the DIP network performs well.(c) Test results of the DIP network applied to the MINST library.

此外,其他傳統ptychography 算法也在結合人工智能算法對相位恢復算法進行優化.例如針對SSP 的神經網絡算法[68],具有浴幕效應的神經網絡算法[69],在無標注數據情況下自主學習相位問題的神經網絡 AutoPhaseNN[70]等.

神經網絡拓展了CDI 的方法學,但是重建策略上仍然存在部分問題.首先,對于監督學習算法,數據集的制作至關重要.現階段大部分監督學習任務大都使用模擬的ptychography 數據,而未提及真實實驗上的重建.模擬數據幾乎未考慮位置誤差、多模態、光源的部分相干,與實際情況出入較大.最后重建效果難以保證.對于非監督學習算法,自動編碼和解碼器雖然有一定優勢.但所需要的數據量大,訓練時間長,并且還需考慮具體實驗中的噪聲影響.針對不同線站所收集的數據形式,需要精心設計相應的數據處理方式來適應神經網絡的訓練.

3 Ptychography 算法并行實例

隨著 ptychography 廣泛的應用,ptychography實驗過程的自動化、智能化計算需求增多.一方面迫切需要集成數據采集、數據處理、圖像重建等的軟件體系.另一方面隨著同步輻射光源性能的提升,將會采集到海量的科學大數據,迫切需要能夠應對海量數據傳輸和處理的高性能軟硬件體系.為了方便讀者能夠及時根據自身的硬件平臺情況測試與應用相關ptychography 軟件,本文按照軟件依賴的硬件平臺劃分為GPU 并行軟件和CPU 并行軟件,分別在3.1 節和3.2 節介紹.

3.1 GPU 算法并行實例

2014 年,Nashed 等[71]實現了一種基于GPU并行計算的ptychography 軟件平臺(圖11).為了提高圖像重建計算效率,將圖像分割后用多個GPU 設備進行并行重建,提出了異步并行法和同步并行法.異步并行法通過MPI 對多個GPU 進行管理,將掃描區域分成多個子區域后分配給不同的GPU 進行圖像重建,然后根據分配位置水平和垂直方向的梯度關系進行圖像拼接.每個GPU 重建的圖像信息是獨立的,各個 GPU 之間不需要共享數據.與異步并行法不同,同步并行法是各個GPU 在處理不同掃描位置的數據時,相鄰區域重疊處的數據在不同GPU 之間會有共享,確保重建圖像的準確性.同步并行的數據共享類似于實驗中的區域重疊,數據的共享也會加快算法的收斂,同時也符合直觀的實驗過程.各類ptychography 圖像重建軟件的GPU并行加速大多按照同步并行的方式.重建區域分割為多個不同子區域會導致重建未重疊區域邊界信息時可能會產生偽影,上述兩方法都有一定程度的克服.

圖11 (a),(b) 分別為GPU 異步并行和同步并行的數據處理示意圖[71];(c),(d) 分別為Ptychopy 軟件的工作流程圖和GUI 界面[52]Fig.11.(a),(b) Schematic diagrams of data processing with GPU asynchronous parallelism and synchronous parallelism,respectively[71];(c),(d) the workflow diagram and GUI interface of the Ptychopy software,respectively[52].

2016 年Mandula 團隊[50]搭建了計算散射、ptychography 的PyNX 軟件工作平臺.最開始利用DM 算法和ePIE 算法進行圖像的重建,并且討論了高斯噪聲條件下,實驗數據的最小化和所有像素強度的平方差的等價性,再利用理論計算和觀測數據的結果計算泊松似然估計得到最好的重建結果.但是PyNX 只有計算散射的模組可以進行GPU 并行加速.軟件在2016 年成功運用歐洲同步輻射光源(European synchrotron radiation facility,ESRF)的數據重建出圖像,并且運用最大似然法來優化更新探針和樣品分布函數.2020 年,PyNX軟件進一步拓展[72],可計算波前傳播、分層成像以及所有的成像操作等.并且對ptychography 模塊進行了更新重寫,增加了計算CDI 和波前的模塊.采用GPU 同步并行加速框架,部分底層采用C++語言使整體運算效率提高.同時,PyNX 支持多種算法混合使用,使重建過程不再拘泥于單一的算法,可以應用不同算法組成重建鏈來探索不同算法組合的可能.PyNX 集成了多種功能,并且高度集成的工具包可以使新算法的開發更加便捷,但沒有GUI 界面會使其入門門檻較高.本文搭建了PyNX 運行環境,重建了不同大小的數據,比較了DM 算法和ML(max-likehood)算法[73]的重建時間和單次重建時間,如圖12 所示.

圖12 (a) 左圖為使用Ptychopy 在同一數據集上測試不同的迭代次數的軟件速度,右圖為使用PyNX 測試模擬數據,分別處理200,500,1000,3000 張探針大小為256×256 的數據集.橫坐標代表數據的大小,縱坐標代表算法實現的時間 (每一步DM 算法會分批次計算LLK(log-likehood)).(b) SHARP 的GPU 并行示意圖和重建流程圖[74].(c) 左圖為PyNX 重建樣品的部分相位圖,右圖為分配給不同 GPU 的掃描位置,部分位置的信息將共享[72]Fig.12.(a) The left figure in (a) shows the software speedup using Ptychopy to test different number of iterations on the same dataset,and the right figure shows the simulated data using PyNX to test and process 200,500,1000,and 3000 datasets with probe size of 256×256,respectively.The horizontal coordinate represents the size of the data,and the vertical coordinate represents the implementation time of the algorithm (LLK (log-likehood) is computed in batches for each DM algorithm step).(b) GPU parallelism of SHARP and the reconstruction flow chart[74].(c) The left figure in (c) shows the partial phase map of the PyNX reconstructed sample,and the right figure shows the scan positions assigned to different GPUs,and the information of some positions will be shared[72].

同年,Marchesini 團隊[74]研制了一個高性能軟件—SHARP,并應用在高級光源(advanced light source,ALS)中.Marchesini 等[75]設計了一套高性能、高效率的算法,通過對算子的操作實現RAAR 算法(relaxed averaged alternating reflections algorithm)來重建實驗過程和實驗數據結果,并且實現了高通量的流分析.GPU 并行計算也遵從同步并行計算的原則,將掃描區域劃分子區域再由不同的GPU 重建.還設計了即時快速反饋系統,可以將實驗結果快速反饋給用戶,這種軟件結構允許用戶對他們的實驗進行直觀、靈活和反應靈敏的監測和控制.數據采集和分析之間需要緊密地整合,以使用戶從中獲得他們所期望的反饋.

2021 年Yue 等[52]針對計算量更大的數據集,實現了Ptychopy 計算軟件.該軟件采用混合式并行計算實現相位恢復.后端基于CPython,C++和CUDA,用戶交互界面和系統控制基于Python庫.它集成了GPU 圖像重建模塊和光束線軟件模塊(如光束線控制、數據收集和存儲模塊),向用戶提供了用戶交互式界面和腳本兩種運行模式.Ptychopy 創建了兩種工作模式,第一種是創建與GPU 數量相等的工作流.控制器會為指定的GPU創建相應的工作流,將圖片重建任務分配給每一個GPU.GPU 采用先入先出的順序處理所分配的作業.這種一對一的GPU 分配適用于作業數多但單個作業數據量小的場景.第二種是創建只有一條工作流,使用所有的GPU 并行計算.適用于單個作業的重建數據超過單個GPU 內存的場景.

3.2 CPU 算法并行實例

Ptypy 軟件[51]可用于比較不同參數設置后的重建結果,作為今后的標準模型框架來降低用戶的入門門檻.Ptypy 通過消息傳遞接口(message passing interface,MPI)將任務分配至每個CPU 節點.同時它還分配了內存數據緩存區,當CPU 核需要處理衍射數據時,緩沖區的數據會并行傳輸至CPU端,如圖13 所示.算法設計上討論了同一次掃描中,探針的形態或是漂移以及樣品的旋轉都會使對應的函數發生變化導致結果不準確.但是在不同的掃描過程中會包含正確的結果,所以不同掃描數據之間可以實現數據共享來提高重建準確性.表1 匯總了當前主流軟件所使用的GPU 型號、使用的算法、單次迭代計算時間以及估算的A100 GPU 計算時間.

圖13 Ptypy 軟件的API 控制與實驗對應示意圖[51],其中Pod 是封裝好得到可調用包Fig.13.Diagram of the API control of the Ptypy corresponding to the experiment step[51],where Pod is wrapped to get the callable package.

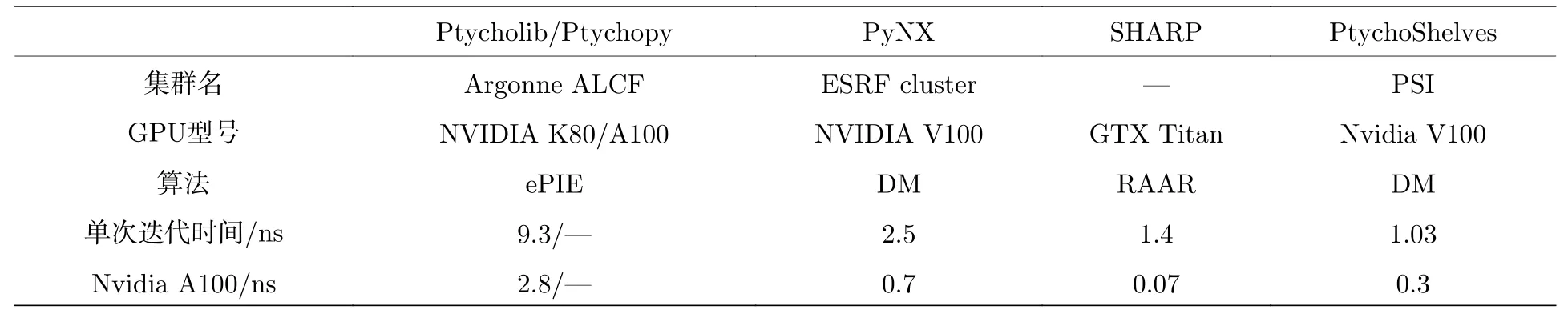
表1 部分軟件計算的硬件信息、使用軟件的算法對單次迭代計算時間的估計值[76],以及使用A100 GPU 的性能速度預測值Table 1.Hardware information for part of the software as well as an estimate of the time for a single iterative computation using the various algorithm[76],and the performance is predicted using the A100 GPU.

3.3 其他算法實例

2020 年瑞士保羅·謝爾研究所(Paul Scherrer Institute,PSI)的Wakonig 團隊[76]基于Matlab 研制了PtychoShelves 軟件.PtychoShelves 的模塊化框架并不依賴于面向對象的實現.新的引擎可以很容易地作為一個單一的函數被添加到引擎目錄中,可以在原有基礎上做任意修改.PtychoShelves使用MPI,OpenMP,Matlab MG 引擎實現了CPU和GPU 的并行加速[77],同時也實現了DM 算法、ePIE 算法和LSQML (least-squares maximumlikelihood)算法[78]的集成和使用.

2021 年Dieter 等[79]開發了Ptychography4.0軟件.該軟件致力于將疊層掃描顯微成像技術借鑒到其他顯微成像領域,同時建立一套廣泛的顯微成像模式標準.Ptychography4.0 軟件包含使用單邊帶方法[80](single side band method)重建掃描電子顯微鏡實驗圖像的振幅和相位等實驗數據以及傳統的ptychography 實驗圖像.Ptychography4.0軟件加入了探測器位置與探針位置的對應關系模塊,可以修正由于位置未對齊而導致的圖像模糊.并且加入了濾波后的移頻操作,使傅里葉變換后的圖像高頻信號部分移至中心,效果明顯.相較于其他軟件,Ptychography4.0 并沒有集成類似PIE 和DM 算法的模塊,而是利用Python 軟件包編寫了一系列與實驗流程相互對應的迭代步驟函數,利用這些函數來實現迭代算法.最后,表2 總結了常用ptychography 的軟件特點及標準化的重建時間[76].

表2 不同軟件的特點以及標準化重建時間[76]Table 2.Characteristics of different software and standardized reconstruction time[76].

4 結論與展望

隨著同步輻射技術的發展,ptychography 面臨的大部分問題逐漸得到解決,但依然存在許多問題.在算法上,高斯和泊松等多種噪聲對迭代算法的影響,實域的物理約束如何在算法中體現等問題都有待優化.在工程上,ptychography 實驗對探針位置精度較為敏感,如何進一步提高實驗系統的穩定性還需進一步優化.

當前主流的ptychography 算法大多都是基于PIE 算法或DM 算法.PIE 算法的易理解性以及與實驗投影過程的一致性,成為大部分相位恢復的主流選擇.但在不同領域PIE 算法面臨的問題也不同,例如在可見光領域信噪比的提升,電子束成像中的輻射損傷和滯后效應[81],X 射線領域光源的部分相干性和位置誤差的影響等.DM 算法來自于晶體學中的差分法理論.但是對于DM 算法的優化較少.Ptychography 作為高分辨成像主流技術之一,在實驗技術上也有一定的發展,例如新的實驗儀器[82].在算法上,有EE-PIE 算法[83],ptychography 結合斷層掃描的新算法[84]應用在生物醫療領域.Ptychography 實驗技術現在已經廣泛運用于材料[40,85],生物[86-88]以及量子態的觀察[89]等領域,具有廣泛的應用前景.

除此之外,ptychography 與人工智能相結合可以使得圖像重建、相位恢復算法實現更高的效率和更佳的質量,在高能同步輻射光源上得到廣泛的應用成為必然的趨勢.然而,一方面隨著四代同步輻射光源技術的發展,光源相干性的提高,納米探針和相干散射等線站采集的數據量將會達到新的高度.且未來束線站會結合多種實驗方法,如Ptychographic Tomography[90,91],Resonant Ptychography[92,93],InSitu Ptychography[94]等.Ptychography 與人工智能兩者都屬于經典的計算密集型任務,對計算能力的要求非常高,現有的計算方法面臨嚴峻挑戰.在未來,光源需要研究更高性能的數據采集和圖像重構軟硬件技術體系,滿足ptychography 算法的海量計算需求.另一方面,隨著高通量、多模態、原位探測器裝置的升級,每秒將會采集海量的科學大數據,高通量大數據的涌入使得傳統方法和機器學習方法都面臨更加嚴重的挑戰.兩者都無法在短時間內進行圖像處理.當前圍繞高能同步輻射光源的數據處理模式主要采用云計算的架構模式,線站將采集的數據通過高帶寬網絡傳輸至云端,在云端進行計算后再傳回本地.這種方式沒有考慮到高能同步輻射光源數據處理的特殊性,無疑會顯著增加傳輸和計算成本.給線站用戶帶來不必要的等待時間.隨著邊緣計算和云計算技術[95]的協同發展,未來光源的發展趨勢是將探測器采集的數據進行線站端和云端協同處理.將一部分計算、存儲資源部署在線站(邊緣端),機器學習訓練等海量計算任務依然發往云端計算集群進行處理.線站端每隔一段時間從云端獲取關鍵的節點模型參數進行本地更新,基于端云協同技術完成本地輕量且重要的計算過程,從而達到快速實時 ptychography 圖像處理和高效實驗處理數據流.最終,通過ptychography 算法本身、人工智能、計算方法交叉研究促進ptychography 方法學的系統發展.