基于傳輸矩陣法的任意變厚度環型壓電超聲換能器*

董宜雷 陳誠 林書玉

(陜西師范大學物理學與信息技術學院,陜西省超聲重點實驗室,西安 710119)

變厚度環型徑向振動壓電超聲換能器可以實現阻抗變換、能量集中,具有輻射面積大、全指向性等優點,在功率超聲、水聲等領域被廣泛應用.由于求解復雜變厚度金屬圓環徑向振動的波動方程比較困難,本文使用傳輸矩陣法將變厚度金屬圓環的徑向振動轉化為 N 個等厚度金屬圓環徑向振動的疊加,得到了任意變厚度金屬薄圓環徑向振動的等效電路圖、共振頻率方程和位移放大系數表達式,分析了錐型、冪函數型、指數型、懸鏈線型金屬圓環的位移放大系數與幾何尺寸的關系.在此基礎上,推導了由任意變厚度金屬圓環和等厚度壓電圓環復合而成的壓電超聲換能器徑向振動的等效電路和共振頻率方程.為了驗證理論結果的正確性,使用有限元軟件進行仿真,所得一階、二階的共振頻率和位移放大系數的數值解與理論解符合較好.本研究給出了任意變厚度金屬圓環徑向振動的普適解,為設計和優化徑向壓電超聲換能器提供了理論指導.

1 引言

徑向振動壓電超聲換能器具有輻射面積大、沿半徑方向有全指向性、接收靈敏度高、結構簡單且性能穩定等優點[1-4],在超聲醫學成像[5,6]、超聲化學反應[7,8]、超聲污水處理[9,10]、水聲通信[11,12]等領域被廣泛應用.徑向復合壓電超聲換能器由金屬圓環和壓電陶瓷圓環復合而成,金屬圓環可以增加壓電陶瓷的散熱,提高其功率容量.為了增大徑向復合壓電超聲換能器輸出端的位移幅值,實現能量集中,輸出端金屬圓環多采用變厚度金屬圓環.變厚度金屬圓環可置于壓電陶瓷環內以實現向內聚能,也可置于壓電陶瓷外從而實現大面積聲能輻射.徑向復合壓電超聲換能器根據金屬圓環軸向厚度沿半徑變化的函數關系被分成錐型、指數型、冪函數型、階梯型等[13-16].

對于變厚度環型壓電超聲換能器的設計和振動分析,通常使用有限元分析法[17]和等效電路法[18,19].等效電路法通過力電類比原理將力學量類比為電學量從而把振動問題簡化.傳統理論研究變厚度環型壓電超聲換能器通常需求解變厚度金屬薄圓環徑向振動的波動方程.基于變厚度徑向振動的波動方程,許龍等[20,21]研究了冪函數型環型聚能器的徑向振動和階梯圓環壓電超聲換能器的徑向振動;劉世清等[22]研究了線性變厚度環型聚能器的徑向振動;王曉宇和林書玉[23]研究了線性變厚度徑向變幅器的耦合振動.但是對于復雜函數變厚度如指數型、懸鏈線型環型壓電超聲換能器,波動方程求解比較困難.傳輸矩陣法可以將連續結構分解成一系列微元結構,一對微元之間通過傳輸矩陣銜接,從而將復雜問題簡單化.基于此,本文提出了用傳輸矩陣法[24]將任意變厚度金屬圓環的徑向振動等效近似為N個等厚度圓環徑向振動疊加的分析方法,得到了任意變厚度金屬圓環徑向振動的共振頻率方程和位移放大系數表達式,以及任意變厚度環型壓電超聲換能器的共振頻率方程.研究了錐型變厚度、冪函數型變厚度、指數型變厚度、懸鏈線型變厚度金屬圓環的共振頻率和位移放大系數與幾何尺寸的關系,以及不同尺寸下錐型變厚度環型壓電換能器徑向一階、二階共振頻率和反共振頻率.

2 變厚度金屬薄圓環徑向振動分析

如圖1 所示,變厚度環型壓電超聲換能器由變厚度金屬內圓環和等厚度壓電陶瓷外圓環組成,變厚度金屬圓環的內環半徑為Rb、外環半徑為Ra、內環半徑處軸向厚度為hb、外環半徑處軸向厚度為ha,等厚度壓電陶瓷圓環的軸向厚度為ha、內環半徑為Ra、外環半徑為Rc.假設變厚度環型壓電超聲換能器的軸向厚度尺寸遠小于徑向尺寸,忽略其縱向振動所帶來的耦合效應,此時環型壓電超聲換能器做純徑向振動.環型壓電超聲換能器的徑向振動由金屬內圓環徑向振動和壓電陶瓷外圓環徑向振動復合而成,因此需要分別研究變厚度金屬圓環的徑向振動和等厚度壓電陶瓷圓環的徑向振動.

圖1 變厚度環型壓電超聲換能器的縱向截面示意圖Fig.1.Schematic diagram of longitudinal section of variable thickness annular piezoelectric ultrasonic transducer.

2.1 變厚度金屬薄圓環徑向振動的等效電路

根據軸向厚度沿半徑的變化函數,變厚度金屬薄圓環可以分成錐型、階梯型、冪函數型等.為了求解任意變厚度金屬薄圓環徑向振動的等效電路,本文采用傳輸矩陣法,將變厚度金屬薄圓環沿半徑方向等分成N個徑向厚度為 Δr的薄圓環.當N足夠大、薄圓環的徑向厚度 Δr的值足夠小時,薄圓環可以看成是軸向厚度不變的等厚度薄圓環.此時,變厚度金屬薄圓環徑向振動的等效電路可以由N個等厚度金屬薄圓環徑向振動的等效電路串聯而成.

根據文獻[25]可知,等厚度金屬薄圓環徑向振動的等效電路如圖2 所示,圖中

圖2 等厚度金屬薄圓環徑向振動的等效電路圖Fig.2.Equivalent circuit of metal thin circular annular in radial vibration.

其 中Z1=ρcS1,Z2=ρcS2,S1=2πR1h1,S2=2πR2h1,R1,R2,h1分別是金屬薄圓環的外半徑、內半徑和軸向厚度,ρ是金屬薄圓環的密度,ν是金屬薄圓環的泊松比,c是金屬薄圓環內的聲速,k是波數,J 是貝塞爾函數,Y 是諾依曼函數.

圖2 中F1,V1,F2,V2分別是第一個薄圓環輸入端與輸出端的徑向受力和徑向振動速度.根據等厚度金屬薄圓環徑向振動的機械等效電路圖和基爾霍夫定律可得:

將輸入端的力學參量F1和徑向振動速度V1移到等號左邊,輸出端的力學參數F2和徑向振動速度V2移到等號右邊,(4)式可以改寫為

其中

由于變厚度金屬薄圓環的徑向應力F和徑向振動速度V連續,所以第2 個薄圓環輸入端的徑向應力和徑向振動速度等于第1 個薄圓環輸出端的力學參數F2和徑向振動速度V2.類比第1 個薄圓環輸入輸出端F,V之間的關系,第2 個薄圓環輸入端參數F2和V2可以由輸出端參數F3和V3表示為

進而第1 個薄圓環輸入端的力參數F1和振動速度V1可以由第2 個薄圓環輸出端參數F3和V3表示為

以此類推,若將變厚度金屬薄圓環分成N個等厚度薄圓環串聯,則第1 個薄圓環輸入端參數F1,V1可以由第N個金屬薄圓環輸出端力參數F N+1和振動速度V N+1表示為

將變厚度金屬薄圓環內外半徑處的力學參量Fa,Fb移至等號左邊,徑向振動速度Va,Vb移動到等號右邊,(12)式可以改寫為

根據電力類比原理以及非互易的二端口等效網絡知識,由(13)式可得到變厚度金屬薄圓環徑向振動的等效電路圖如圖3 所示.

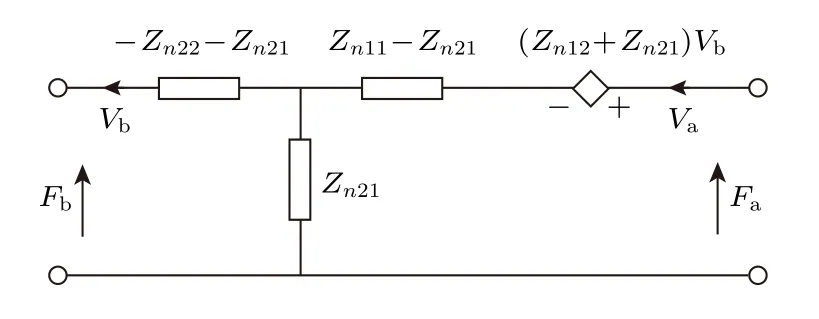
圖3 變厚度金屬薄圓環徑向振動的等效電路圖Fig.3.Equivalent circuit diagram of metal thin annular with variable thickness in radial vibration.

當變厚度金屬薄圓環的輸出端自由,即Fb=0時,變厚度金屬薄圓環徑向振動的共振頻率方程為

此時,變厚度金屬薄圓環的位移放大系數為

2.2 變厚度金屬薄圓環徑向振動性能分析

根據任意變厚度金屬薄圓環徑向振動的等效電路圖,得到其共振頻率方程和位移放大系數表達式.選取N=100,使用數值計算軟件MATLAB 根據(14)式和(15)式分別計算①錐型金屬圓環、②冪函數型金屬圓環、③指數型金屬圓環和④懸鏈線型金屬圓環徑向振動的共振頻率和位移放大系數.錐型金屬圓環的厚度隨半徑以線性函數規律變化,冪函數型金屬圓環的厚度隨半徑以冪函數h(r)=m/rn規律變化,指數型金屬圓環的厚度隨半徑以指數函數h(r)=ae-βr規律變化,懸鏈線型金屬圓環的厚度隨半徑以懸鏈線函數h(r)=hacosh[γ(Ra-r)]規律變化.金屬圓環的尺寸參數是: 內環半徑Rb=25 mm,外環半徑Ra=50 mm,外環半徑處厚度ha=10 mm,內環半徑處厚度hb的取值范圍為 1 —10 mm .選取金屬圓環的材料為鋁,其材料參數為: 密度ρ=2700 kg/m3,楊氏模量E=70 GPa,泊松比υ=0.33 .為了與理論計算結果進行對比,使用有限元軟件COMSOL6.0 對上述材料尺寸的金屬圓環進行仿真模擬.4 種變厚度金屬圓環的一階、二階徑向共振頻率和位移放大系數的理論解和數值解如表1 和表2 所示.表1 和表2 中f和f*分別表示變厚度金屬圓環徑向振動共振頻率的理論解和數值解,M *,M **分別表示變厚度金屬圓環位移放大系數的理論解和數值解,相對誤差計算方法為:Δ f=|(f -f*)/f*|,=|(M*-M**)/M**|.

表1 變厚度金屬圓環徑向一階、二階共振頻率Table 1.Radial first and second order resonance frequencies of metal rings with variable thickness.

表2 變厚度金屬圓環徑向一階、二階共振位移放大系數Table 2.Radial first and second order resonance displacement amplification coefficients of metal rings with variable thickness.

4 種變厚度金屬圓環(①錐型金屬圓環、②冪函數型金屬圓環、③指數型金屬圓環、④懸鏈線型金屬圓環)徑向一階、二階共振頻率和位移放大系數隨內外環厚度比ha/hb的變化曲線如圖4 和圖5所示,其中-T 為理論結果,-FEM 為有限元仿真結果.

由圖4 可知,4 種變厚度金屬圓環的一階共振頻率隨ha/hb的增大而減小,當內環半徑處的厚度hb減小時,金屬圓環等效半徑增大,共振頻率減小.二階共振頻率隨著ha/hb的增大而增大,徑向二階共振頻率受金屬圓環等效質量影響較大,當內環半徑處厚度hb減小時,金屬圓環等效質量減小,共振頻率向高頻偏移.另外,4 種變厚度金屬圓環一階共振頻率的數值解幾乎在理論解隨ha/hb的變化曲線上,二階共振頻率的數值解隨ha/hb的變化趨勢與理論解一致,且相對誤差在2%以內,這表明傳輸矩陣法可以用來研究任意變厚度金屬圓環的徑向振動.由于徑向二階的聲波波長比一階小,耦合振動效應較為明顯,使得徑向二階共振頻率的相對誤差大于徑向一階.

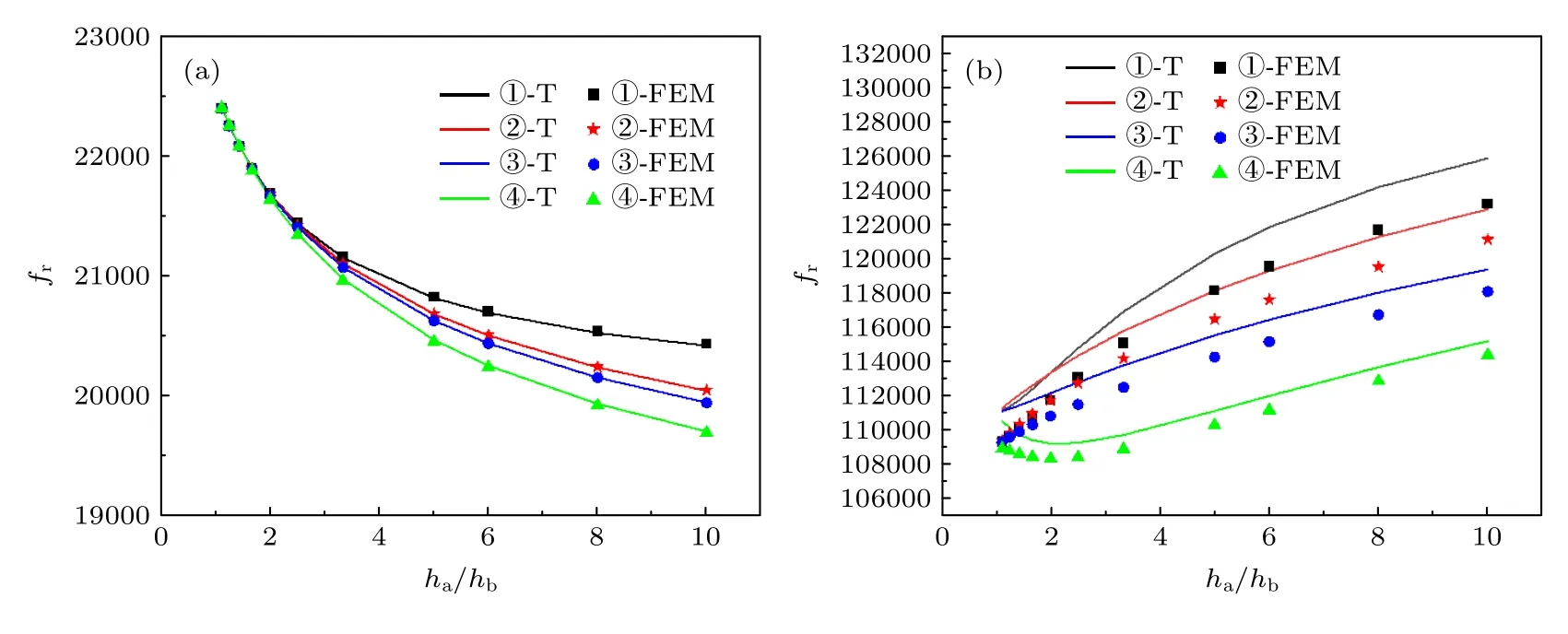
圖4 4 種變厚度金屬圓環一階、二階徑向共振頻率與 ha/hb 的關系 (a)一階徑向共振;(b)二階徑向共振Fig.4.The relationship between the first and second order radial resonance frequencies of four kinds of variable thickness metal rings and thickness ratio ha/hb : (a) First-order radial resonance;(b) second-order radial resonance.

由圖5 可知,4 種變厚度金屬圓環(①錐型金屬圓環、②冪函數型金屬圓環、③指數型金屬圓環和④懸鏈線型金屬圓環)一階共振、二階共振的位移放大系數隨ha/hb的增大而增大,這表明內環半徑處的厚度hb越小,環型聚能器向內聚能的效果越好.整體來看,一階共振的位移放大系數從大到小依次是錐型、冪函數型、指數型、懸鏈線型,二階共振的位移放大系數從大到小依次是懸鏈線型、指數型、冪函數型、錐型.4 種聚能器的一階共振位移放大系數較小,在1.2 左右,二階共振位移放大系數較大,在2—4 范圍.這表明位移放大系數不止與厚度隨半徑的函數變化關系有關,還與工作模態相關.另外,4 種聚能器徑向一階、二階共振位移放大系數的數值解基本與理論解隨ha/hb的變化曲線重合,驗證了理論解的正確性.

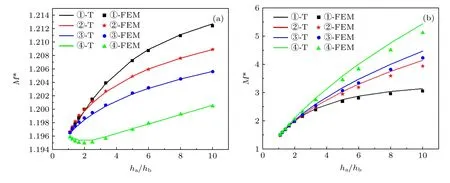
圖5 4 種變厚度環型聚能器一階和二階徑向共振位移放大系數隨 ha/hb 的變化曲線 (a)一階徑向共振;(b)二階徑向共振Fig.5.The relationship between the first and second order radial resonance displacement amplification coefficient and thickness ratio ha/hb of four kinds of variable thickness metal rings: (a) First-order radial resonance;(b) second-order radial resonance.

2.3 N 取值對計算精度的影響

本文將變厚度金屬圓環的徑向振動等效近似為N個等厚金屬圓環徑向振動的疊加,N的取值大小對計算精度影響較大.選取錐型變厚度金屬圓環的材料為鋁,尺寸參數是: 內環半徑Rb=25 mm,外環半徑Ra=50 mm,外環半徑處厚度ha=10 mm,內 環半 徑處 厚度hb=1 mm .錐型變厚度金屬圓環的一階、二階徑向共振頻率隨N的變化趨勢如圖6 所示,由圖6 可知,當N的取值大于50 時,錐型金屬圓環徑向一階、二階共振頻率趨于穩定,即等厚度金屬圓環的徑向厚度小于0.5 mm時,共振頻率的計算精度滿足要求.

圖6 錐型金屬圓環的一階、二階徑向共振頻率與N 的關系 (a)一階徑向共振;(b)二階徑向共振Fig.6.The relationship between the first and second order radial resonant frequencies of conical metal rings and N: (a) First-order radial resonance;(b) second-order radial resonance.

3 環型壓電換能器徑向振動分析

3.1 變厚度環型壓電換能器徑向振動的等效電路

其 中,Zra=ρpcpSra,Zrc=ρpcpSrc,Sra=2πRaha,Src=2πRcha,ha是壓電陶瓷圓環的厚度,kp和cp分別是壓電陶瓷圓環的波數和徑向聲速.

變厚度金屬薄圓環與壓電陶瓷薄圓環在半徑Ra處滿足徑向應力連續和振動速度連續,因此,變厚度金屬薄圓環徑向振動與壓電陶瓷薄圓環徑向振動的等效電路串聯,可得到環型壓電超聲換能器徑向振動的等效電路圖如圖8 所示.

當環型壓電超聲換能器內外表面所受徑向作用力為0 時,即圖8 中Fb=Fc=0 時,環型壓電超聲換能器電端輸入阻抗表達式為

圖8 環型壓電超聲換能器徑向振動的等效電路圖Fig.8.Equivalent circuit diagram of circular piezoelectric ultrasonic transducer in radial vibration.

其中

圖7 壓電陶瓷圓環徑向振動的等效電路圖Fig.7.Equivalent circuit diagram of piezoelectric ceramic annular in radial vibration.

因此環型壓電超聲換能器徑向振動共振頻率方程為

徑向振動反共振頻率方程為

3.2 變厚度環型壓電超聲換能器徑向振動性能分析

根據(21)式和(22)式可以求得任意變厚度環型壓電超聲換能器徑向振動的共振頻率和反共振頻率,本文以錐型變厚度環型壓電超聲換能器為例,錐型壓電超聲換能器由錐型變厚度金屬薄圓環和等厚度壓電陶瓷圓環組成.變厚度金屬薄圓環的尺寸參數是: 內環半徑Rb=20 mm,外環半徑Ra=40 mm,外環半徑處厚度ha=10 mm,內環半徑處厚度hb的取值范圍為 1 —10 mm .壓電陶瓷圓環的尺寸參數是: 內環半徑Ra=40 mm,外環半徑Rc=45 mm,壓電陶瓷圓環的厚度ha=10 mm .選取金屬圓環的材料為鋁,選取壓電陶瓷圓環的材料為PZT-4,其材料參數是:ρp=7500 kg/m3,為了與理論計算結果進行對比,使用有限元軟件COMSOL6.0 對上述材料尺寸的環型壓電超聲換能器進行仿真模擬,模擬所得一階共振、二階共振的振型圖如圖9所示.部分尺寸錐型變厚度環型壓電超聲換能器一階、二階共振頻率和反共振頻率的理論解和數值解如表3 和表4 所示.

表3 錐型變厚度環型壓電換能器一階共振頻率和反共振頻率Table 3.The first-order resonant frequency and anti-resonant frequency of conical variable thickness annular piezoelectric transducer.

表4 錐型變厚度環型壓電換能器二階共振頻率和反共振頻率Table 4.The second-order resonant frequency and anti-resonant frequency of conical variable thickness annular piezoelectric transducer.

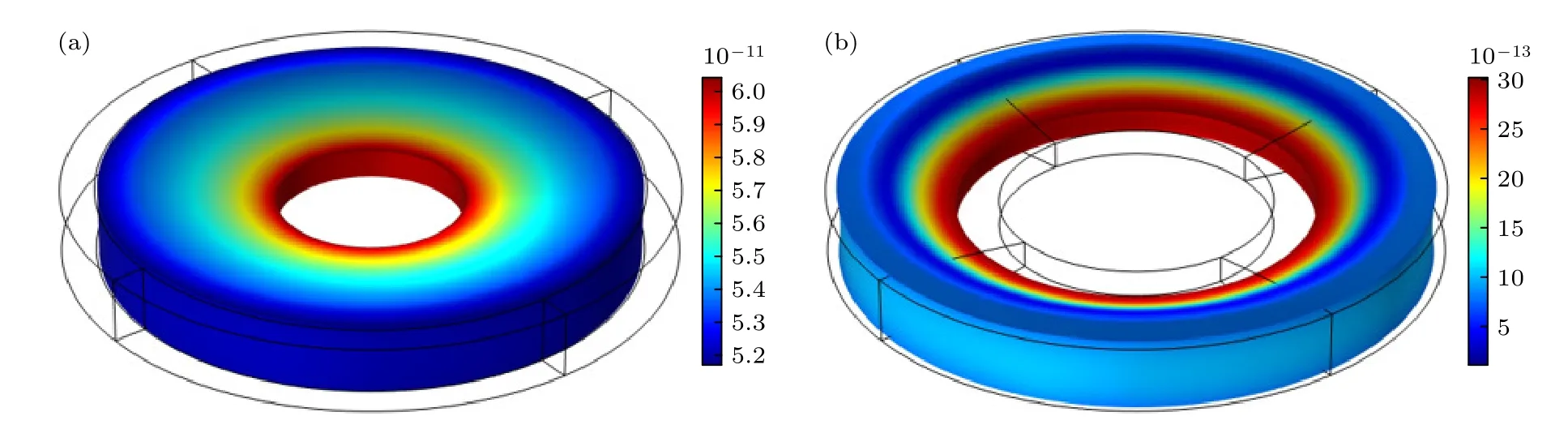
圖9 錐型變厚度環型壓電超聲換能器一階、二階徑向共振振型圖 (a)一階徑向共振;(b)二階徑向共振Fig.9.First-order and second-order radial resonance mode shapes of conical variable thickness annular piezoelectric ultrasonic transducer: (a) First-order radial resonance;(b) second-order radial resonance.

表3 和表4 中f和f*分別表示錐型變厚度環型壓電超換能器徑向振動共振頻率的理論解和數值解,Keff和分別為其有效機電耦合系數的理Δ=|(f -f*)/f*|論解和數值解,相對誤差 .由表3和表4 可知,徑向一階振動共振頻率的理論解和數值解吻合非常好,相對誤差不超過0.2%,徑向二階振動共振頻率的理論解和數值解吻合較好,相對誤差不超過3%.這驗證了基于傳輸矩陣法的任意變厚度環型壓電超聲換能器徑向振動共振頻率理論解的正確性.由于徑向二階的聲波波長比一階小,耦合振動效應較為明顯,二階共振頻率、反共振頻率的相對誤差大于徑向一階.

錐型變厚度環型壓電超聲換能器徑向一階、二階共振頻率和反共振頻率隨內外環厚度比ha/hb的變化曲線如圖10 所示.由圖10 可知,徑向一階共振頻率、反共振頻率隨著隨ha/hb的增大而減小,徑向二階共振頻率、反共振頻率隨著隨ha/hb的增大而增大.隨著ha/hb的增大,一階、二階的共振頻率和反共振頻率的差值增大,有效機電耦合系數增大.

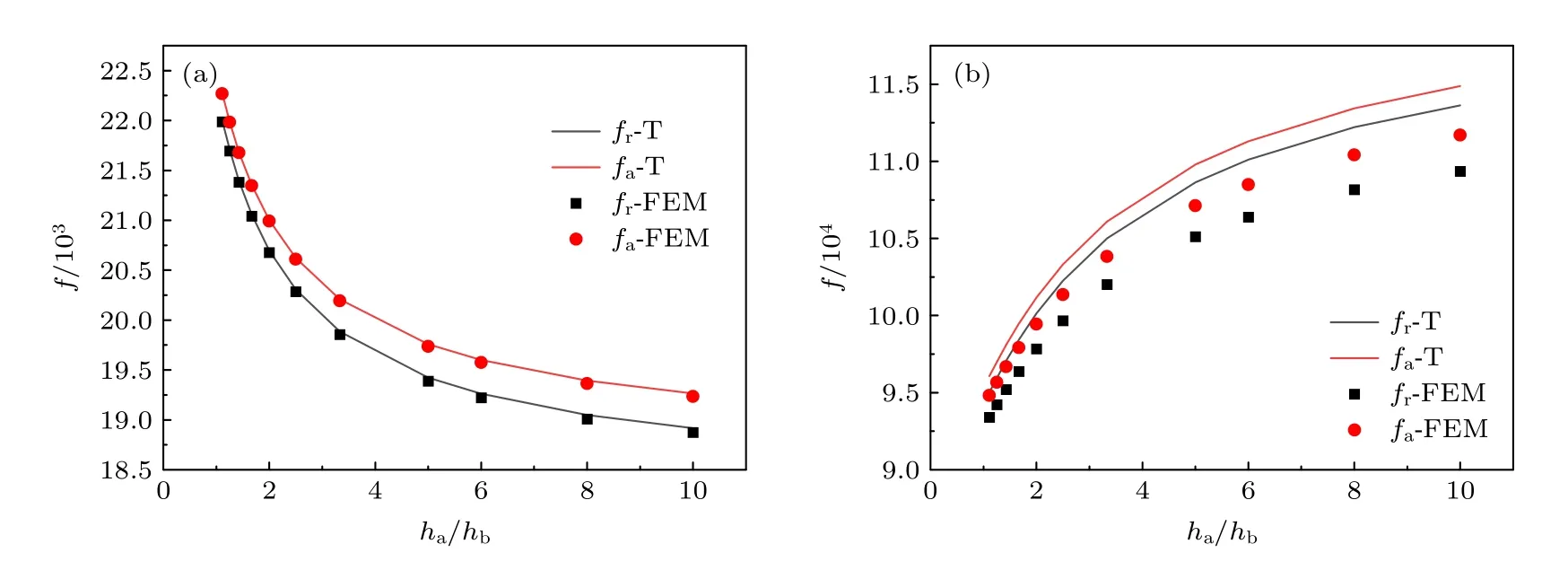
圖10 錐型變厚度環型壓電超聲換能器一階、二階徑向共振頻率和反共振頻率與 ha/hb 的關系 (a)一階共振和反共振;(b)二階共振和反共振Fig.10.The relationship between the first and second order radial resonance frequency and the anti-resonance frequency and the thickness ratio ha/hb of a conical variable thickness annular piezoelectric ultrasonic transducer: (a) The first-order radial resonance and anti-resonance;(b) the second-order radial resonance and anti-resonance.

4 結論

本文基于傳輸矩陣法將變厚度金屬圓環的徑向振動轉化為N個等厚度金屬圓環徑向振動的疊加,得到了任意變厚度金屬薄圓環徑向振動的等效電路圖、共振頻率方程和位移放大系數表達式,分析了錐型、冪函數型、指數型、懸鏈線型金屬圓環的位移放大系數隨內外環厚度比ha/hb的變化關系.研究發現,整體上一階共振頻率隨ha/hb的增大而減小,二階共振頻率隨著ha/hb的增大而增大.一階、二階的位移放大系數均隨ha/hb的增大而增大,且徑向一階共振位移放大系數從大到小依次是錐型、冪函數型、指數型和懸鏈線型,徑向二階共振位移放大系數從大到小依次是懸鏈線型、指數型、冪函數型、錐型.在此基礎上,推導了由任意變厚度金屬圓環和壓電陶瓷圓環復合而成的壓電超聲換能器徑向振動的等效電路和共振頻率方程,計算了不同尺寸的環型壓電換能器的共振頻率和反共振頻率,為了驗證理論計算結果的正確性,使用有限元軟件進行仿真模擬,模擬所得數值解與理論解符合較好,最大相對誤差不超過3%.