電子溫度各向異性對螺旋波等離子體中電磁模式的傳播及功率沉積特性的影響*

李文秋 唐彥娜 劉雅琳 王剛

(中國科學院空天信息創新研究院,北京 100190)

采用考慮粒子溫度各向異性熱等離子體介電張量模型,借助磁化、均勻密度分布等離子體中電磁波的一般色散關系,在低磁場、低氣壓螺旋波等離子體典型參量條件下,理論分析了電子溫度各向異性對電磁模式傳播特性和角向對稱模功率沉積的影響.研究結果表明: 對于給定的縱向靜磁場B0 (或波頻率ω),存在一個臨界波頻率ωcr (或縱向靜磁場B0,cr),當ω ＞ ωcr (或B0 ＜ B0,cr)時,電子回旋諧波遭受的阻尼開始顯著增大;相比粒子溫度各向同性情形,粒子溫度各向異性徹底改變了波的傳播特性,即相位常數和衰減常數均出現峰值現象;在考慮電子有限拉莫爾半徑效應和電子溫度各向異性情形下,Trivelpiece-Gould (TG)波碰撞阻尼在整個電磁波功率沉積中占據主導地位,電子縱向溫度Te,// 存在某一臨界值,在此臨界值處TG 波功率沉積出現峰值Pabs,TG,且隨著Te,⊥/Te,// 的減小,此功率沉積峰值 Pabs,TG 逐漸增強.

1 引言

在磁層中傾斜于背景磁場傳播的無界Whistler 波,可通過電子回旋共振機制加熱電子[1-4],其電磁模分支在有界、磁化條件下演化為螺旋波(helicon)[5],該螺旋波可滲入等離子體內部傳播而產生高密度等離子體[6-8].自1985 年首次在實驗中觀測到高密度(≥ 1×1013cm-3)特性以來[9],螺旋波等離子體即得到廣泛的應用,在NASA 的NextSTEP(next space technologies for exploration partnerships)先進空間電推進系統(包含VASIMR(variable specific impulse magnetoplasma rocket),ELF(electrodeless Lorentz force)和Nested Hall電推進系統)項目中,螺旋波等離子體源被用來產生初級低溫等離子體[10-16];在半導體電路刻蝕中,螺旋波等離子體源被用來刻蝕產生納米級高分辨率芯片[17-19];在核聚變應用領域中,借助高功率螺旋波等離子體源產生的高密度氘等離子體,研究者們正在分析等離子體-材料表面互作用機理[20-23].盡管關于螺旋波等離子體的應用已經十分深入,但其高密度特性背后的物理機制至今仍未完全被揭示[24-27],1991 年,Chen[28]提出朗道阻尼(Landua damping)機制,認為螺旋波是通過朗道阻尼機制產生高能電子從而實現波能量的沉積;后來,Chen和Blackwell[29,30]通過測量螺旋波等離子體中的電子能量分布函數,發現螺旋波放電中并不存在強朗道阻尼產生的高能電子,因此推翻了朗道阻尼加熱機制.2002 年,Kline 等[31]發現在螺旋波等離子體中存在由靜電慢波的局域低雜化共振離子朗道阻尼引起的離子加熱現象.2006 年,在高頻螺旋波等離子體中,Eom 等[32]在實驗中發現當靜磁場低于某一閾值時,存在由螺旋波向TG(trivelpiecegould)波的模式轉換現象.2012 年,Tarey 等[27]在綜合分析的基礎上發現低氣壓(0.2—0.3 mTorr,1 Torr=133 Pa)情形下存在的熱電子可能是由TG 波的朗道阻尼機制導致.2020 年,Cho[33]通過理論分析發現螺旋波和TG 波在功率沉積中的占比受到模式轉換和碰撞頻率的影響.2014 年,趙高等[34]通過實驗研究了螺旋波等離子體的放電特性,觀測到電子密度在射頻功率增加過程中出現兩次大幅增大.2019年,平蘭蘭等[35]通過計算程序,分析了靜磁場強度和中心等離子體密度對功率沉積及其分布的影響.

作為螺旋波等離子體中被觀測到的電子溫度各向異性現象[36,37],其與波功率沉積之間的關系至今未有研究.為詳盡研究螺旋波等離子體中高密度現象背后的物理機制,本文采用熱等離子體介電張量模型,在螺旋波等離子體典型參量條件下,分析了電子溫度各向異性對波傳播和功率沉積特性的影響,所得結果為進一步理解螺旋波等離子體高密度物理機制提供了線索.

2 理論模型

螺旋波天線放電產生徑向密度均勻分布的等離子體柱,其被厚度可忽略的玻璃管包裹,半徑r=a的等離子體柱浸沒在縱向(定義沿Z軸為縱向,用符號// 表示;垂直于z軸方向為橫向,用符號⊥表示)靜磁場中,玻璃管外為真空.假定等離子體柱中的離子攜帶單位正電荷,且具有有限溫度.圖1 所示為螺旋波等離子體柱示意圖.

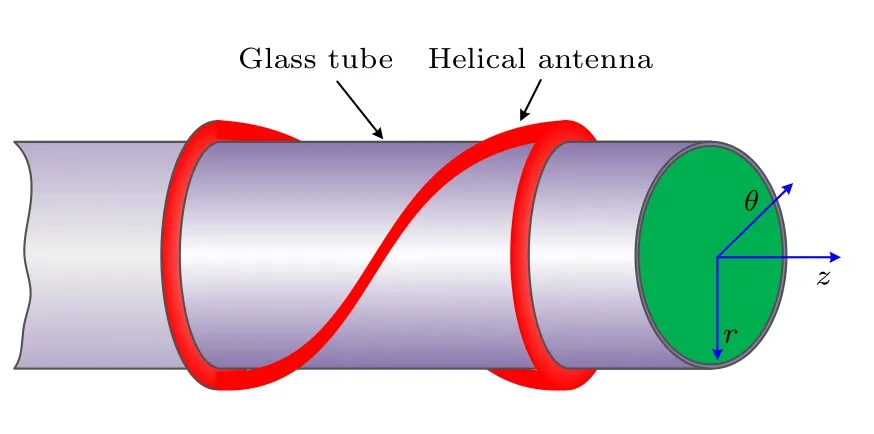
圖1 螺旋波等離子體柱示意圖Fig.1.Cross section of helicon plasma column.

在麥克斯韋分布等離子體中,假定波矢k在rz平面,在粒子溫度各向異性和粒子存在縱向漂移速度情形下,等離子體介電張量的元素可表示為[38]

在均勻密度、磁化等離子體中傳播的電磁波,其具有如下一般色散關系[42]:

式中κ ∧,κ ∨及κ∠為等離子體介電張量元素;k0=ω/c,c為光速;R=κ∧+κ∨;L=κ∧-κ∨.在無界等離子體中,(10)式對應Whistler 波的色散關系,它有兩個關于橫向波數k⊥的分支: 具有較小橫向波數的電磁分支和具有較大橫向波數的靜電分支;對應在有界等離子體中,電磁分支演化為螺旋波,而靜電分支演化為TG 波.對于右手圓極化占主導地位的Whistler 波,其傳播方向平行于縱向靜磁場,由此得到其色散關系:

注意到(11)式忽略了粒子的有限拉莫爾半徑效應,但包含所有的回旋諧波次數,且考慮粒子縱向漂移速度的影響.

得到如下關于描述電磁波傳播的微分方程:

求解(14)式,分別得到等離子體柱內和外部真空區域中的磁場縱向分量[44]:

利用邊界條件,磁場切向分量在分界面連續,得到描述等離子體中關于本征電磁模式的色散關系:

元素由表1 給出.

表1 色散關系元素Table 1.Elements of dispersion relation.

在螺旋波等離子體中,波的能量沉積通常由粒子間的碰撞效應和動理學效應引起,其中動理學效應引起的阻尼機制主要包含朗道阻尼和回旋阻尼(cyclotron damping),縱向熱速度略小于電磁波相速的粒子通過共振作會吸收波的能量造成波衰減,這稱為朗道阻尼;在垂直于外部磁場方向上作回旋運動的粒子,當其回旋頻率與平行于磁場傳播的電磁波頻率相同時,可以與粒子發生共振,形成波的回旋阻尼.這些阻尼機制在不同的參量情形下起著不同的作用,由這些阻尼機制產生的波功率沉積可由下式給出:

本文僅研究角向對稱模(m=0)的能量沉積特性,在計算過程中,首先采用尋根函數fsolve 求解超越色散方程(18)式,然后借助橫向波數得到精確場分布,最后利用(19)式計算波的功率沉積.本文假定工質氣體為氬氣(A=40),射頻波頻率為13.56 MHz,等離子體柱半徑a=3 cm,離子-電子縱向溫度比Ti,///Te,//=0.1 .

3 數值計算與結果分析

在分析波功率沉積特性之前,先對螺旋波等離子體中存在的兩種典型波模式之間的耦合特性進行分析.在ω/ωce=0.1參量條件下,利用(10)式,計算得到不同氣壓條件下Whistler 波靜電(electro static,ES)分支與電磁(electro magnetic,EM)分支的耦合曲線.圖2 顯示,在當前高密度、低磁場參量情形下,ES 分支與EM 分支在模式耦合層(mode coupling surface,MCS)發生模式耦合;每個縱向波數對應兩個橫向波數,ES 分支具有較大橫向波數,EM 分支具有較小橫向波數;隨著工質氣體氣壓的增大,模式耦合層的位置發生明顯改變,但在典型螺旋波等離子體溫度條件下,工質氣體氣壓的增大并未明顯改變靜電波與電磁波的傳播特性,這表明工質氣體氣壓對Whistler 波的傳播影響并不顯著.

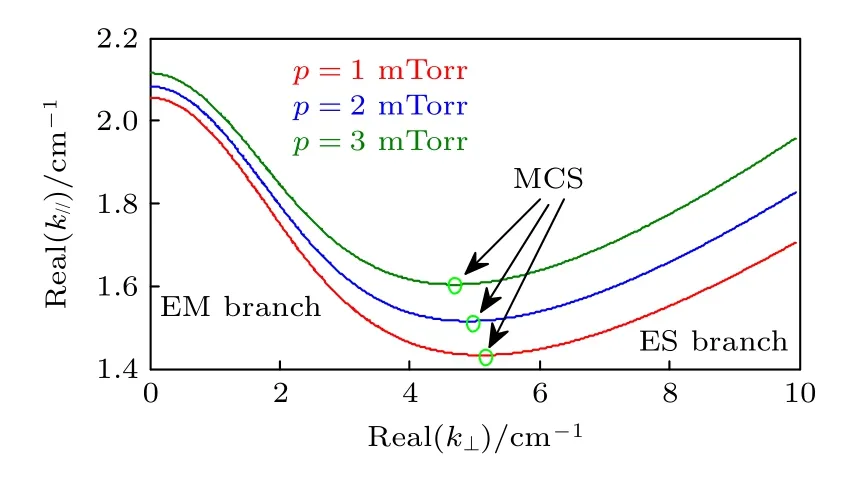
圖2 Whistler 波色散特性Fig.2.Dispersion characteristic of whistler wave.

由于碰撞阻尼和回旋阻尼的存在,導致計算得到的縱向波數具有復數形式,即k//=β+jα,其中β為相位常數(單位為rad/cm),α為衰減常數(單位為Np/cm).基于(11)式,忽略粒子縱向漂移速度,在n0=1×1013cm-3,B0=48 Gs (1 Gs=10—4T),Te,//=3 eV 及p=1 mTorr 參量條件下,計算得到Whistler 波的n=1 次回旋諧波的相位常數和衰減常數如圖3 所示,從圖3 可以看到,在給定的參量區間ω/ωce∈(0,0.4) 內,對于相位常數,其幅值從參量區間初始處便隨著波頻率的增大而陡峭變大;而對于衰減常數,則存在一個閾值 (ω/ωce)cr,低于此閾值,波阻尼極其微小可以忽略,而超過此閾值時,波遭遇的阻尼開始顯著增大.當電子溫度各向異性因子Te,⊥/Te,//=0.5 時,圖3 顯示波在歸一化頻率閾值 (ω/ωce)cr≈0.1 處開始遭受顯著阻尼,當Te,∧/Te,//變 為1.0 和1.5 時,(ω/ωce)cr分別變為0.15 和0.28;另一方面,對于給定的歸一化頻率(ω/ωce),電子橫向溫度越大,波的阻尼強度越小,這是因為當電子橫向溫度大于縱向溫度時,電子與波的互作用時間主要發生在橫向,這時回旋阻尼是主要的波能量衰減機制,而由于回旋阻尼在當前參量條件下并不顯著,所以衰減常數幅值相比溫度各向同性條件下要小;而當電子橫向溫度小于縱向溫度時,電子與波的互作用時間主要發生在縱向,這時碰撞阻尼和朗道阻尼是主要的波能量衰減機制,在當前參量條件下,縱向的碰撞阻尼和朗道阻尼強度大于橫向的回旋阻尼,所以衰減常數幅值相比溫度各向同性條件下大.

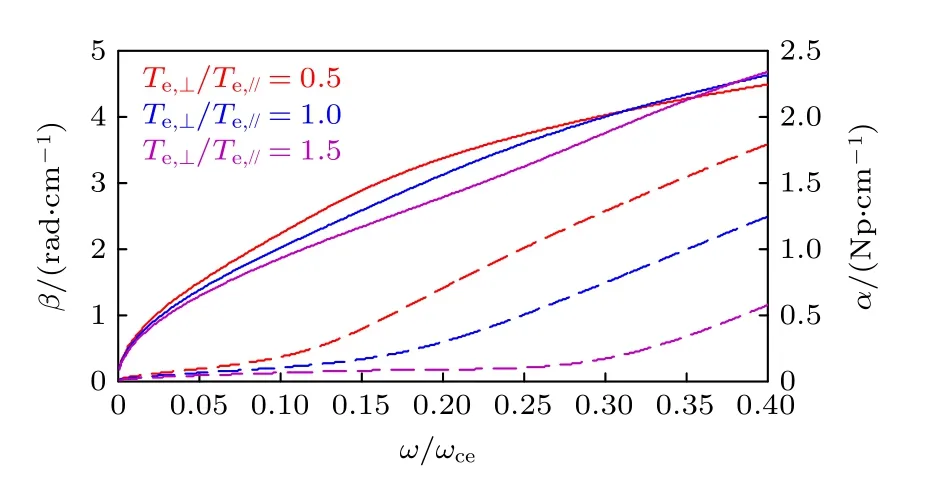
圖3 電子溫度各向異性對Whistler 波n =1 次回旋諧波傳播常數的影響 (實線代表相位常數,虛線代表衰減常數)Fig.3.Effect of electron temperature anisotropy on the propagation characteristic of the n =1 electron cyclotron harmonic (the solid lines represent the phase constant,and the dashed lines represent the attenuation constant).

忽略粒子縱向漂移速度,在n0=1×1013cm-3,p=1 mTorr,Te,⊥=Te,//=3 eV 參量條件下,Whistler波n=1,2,3 次回旋諧波的傳播常數隨縱向靜磁場(以ω/ωce形式給出)的變化特性如圖4 所示.結果表明: 在給定波頻率條件下,隨著縱向靜磁場逐漸減小(ω/ωce逐漸增大),n=1,2,3 次回旋諧波的衰減常數在不同閾值 (ω/ωce)cr處開始顯著陡升,而相位常數在變量區間初始處便開始陡升;同時注意到,當縱向靜磁場逐漸減小時,n=1 次回旋諧波最先遭遇回旋阻尼,且在3 個諧波的回旋阻尼中占據主導地位.

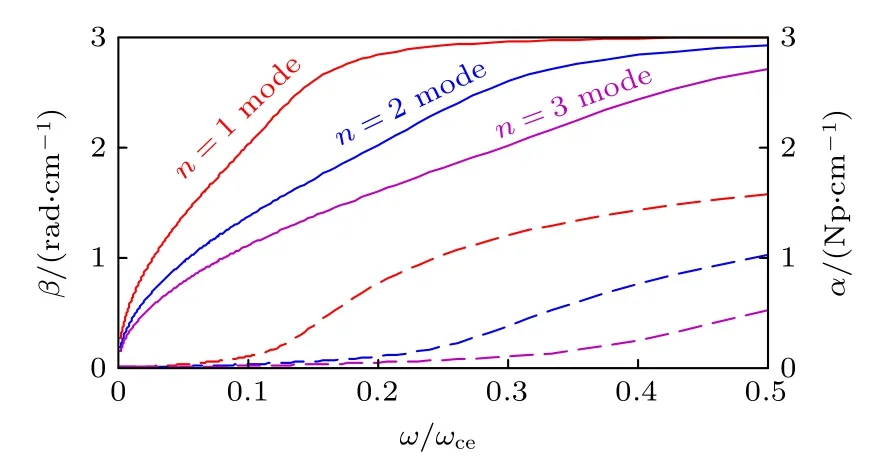
圖4 電子溫度各向同性情形下n=1,2,3 次回旋諧波傳播常數對縱向靜磁場的依賴關系 (實線代表相位常數,虛線代表衰減常數)Fig.4.Dependence of propagation characteristic of the n=1,2,3 electron cyclotron harmonics on magnetic field in the case of electron temperature isotropy (the solid lines represent the phase constant,and the dashed lines represent the attenuation constant).

為進行對照,分析電子溫度各向異性對不同諧波回旋阻尼的影響,采用與圖4 一樣的參量條件,在電子溫度各向異性因子Te,⊥/Te,//=0.1 條件下,n=1,2,3 次回旋諧波的傳播常數隨縱向靜磁場(以ω/ωce的形式給出)的變化關系如圖5 所示.由圖5 可知,在變量區間ω/ωce∈(0,0.5),對于n=1次回旋諧波,隨著縱向靜磁場逐漸減小(ω/ωce逐漸增大),相位常數先增大后減小,在ω/ωce≈0.11處取得峰值;而衰減常數所代表的回旋阻尼在ω/ωce≈0.11 處開始劇烈陡升,當ω/ωce＞0.3 時趨于平穩.與n=1 次回旋諧波情形類似,n=2,3 次回旋諧波的相位常數也在不同ω/ωce處取得峰值,衰減常數在不同ω/ωce處開始顯著增大.聯合分析相位常數和衰減常數曲線可以發現,衰減常數顯著陡升和相位常數出現峰值兩者對應的橫坐標ω/ωce非常接近.這些現象結合圖4 表明: 電子溫度各向異性從根本上改變了波的傳播特性,即電子溫度各向異性的存在使得各次回旋諧波分別對應一個最佳的縱向靜磁場強度,在此最佳縱向靜磁場強度下,各個回旋諧波開始遭受顯著回旋阻尼.

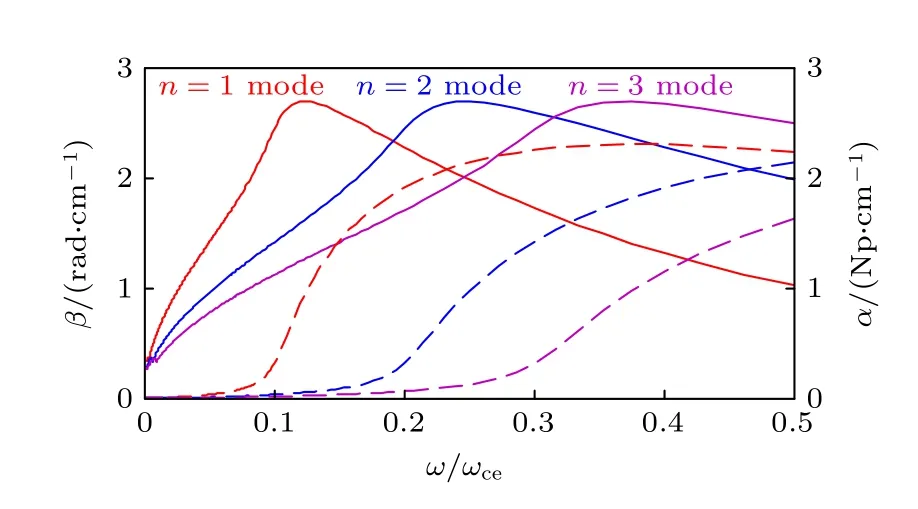
圖5 電子溫度各向異性情形下n =1,2,3 次回旋諧波傳播常數對縱向靜磁場的依賴關系 (實線代表相位常數,虛線代表衰減常數)Fig.5.Dependence of propagation characteristic of the n =1,2,3 electron cyclotron harmonics on magnetic field in the case of electron temperature anisotropy (The solid lines represent the phase constant,and the dashed lines represent the attenuation constant).

作為影響回旋諧波阻尼特性的兩個重要參量,電子溫度各向異性和縱向漂移效應可能對波產生顯著的衰減效應.在n0=1×1013cm-3,ω/ωce=0.3,p=1 mTorr,Te,//=3 eV 參量條件下,計算得到兩個參量對回旋諧波衰減常數的影響結果如圖6 所示.在忽略粒子縱向漂移速度條件下,圖6(a)所示為電子溫度各向異性對n=1,2,3 次回旋諧波衰減特性的影響,由圖6 可知,在變量區間Te,⊥/Te,//∈(0.01,10),隨著Te,⊥/Te,//的增大,3 個回旋諧波的衰減常數均單調減小,且在Te,⊥/Te,//=1處急劇減小,之后3 個回旋諧波在不同的Te,⊥/Te,//臨界值處衰減常數降至零.這是因為,當電子橫向溫度遠小于縱向溫度(Te,//=3 eV)時,波在橫向遭受的回旋阻尼非常弱,此時波遭受的阻尼主要來自縱向的碰撞效應和朗道阻尼效應;當電子橫向溫度大于縱向溫度時,波遭受的阻尼主要來自橫向的回旋阻尼,而由于回旋阻尼在當前參量條件下非常弱,故隨著Te,⊥/Te,//的持續增大,波遭受的阻尼急劇減小.在粒子溫度各向同性條件下(Te,⊥/Te,//=1),圖6(b)所示為縱向漂移效應對3 個回旋諧波衰減特性的影響,與圖6(a)中的曲線變化特性類似,圖6(b)顯示3 個回旋諧波的衰減常數均隨著電子縱向漂移速度的增大而單調減小.這是由于電子縱向漂移速度的存在擾動了波的相速、電子熱速度及回旋頻率之間的共振平衡條件,從而造成回旋阻尼和朗道阻尼效應的減弱,且隨著漂移速度的逐漸增大,這種擾動越發嚴重,圖6(b)說明當漂移速度超過電子熱速度時,波的回旋阻尼和朗道阻尼變得非常微弱.

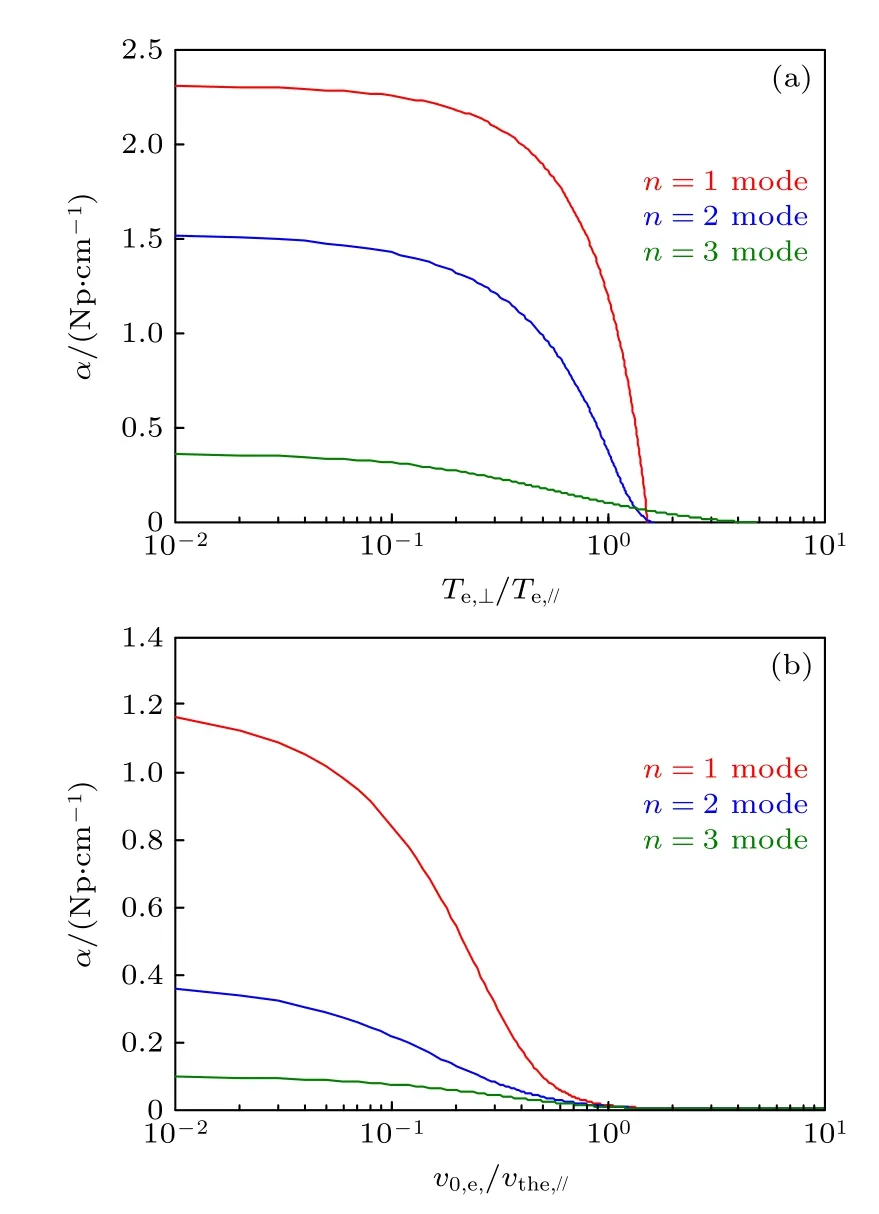
圖6 n =1,2,3 次回旋諧波衰減常數隨 (a) 電子溫度各向異性和 (b) 電子縱向漂移速度的依賴關系Fig.6.Dependence of attenuation constant of the n =1,2,3 electron cyclotron harmonics on (a) the electron temperature anisotropy and (b) electron parallel drift velocity.

在計算螺旋波與TG 波功率沉積之前,首先有必要對介電張量元素中的有限拉莫爾半徑效應因子進行詳細分析.n0=1×1013cm-3,p=1 mTorr,Te,//=3 eV,Te,⊥/Te,//=0.1 參量條件下,在變量區間ω/ωce∈(0.01,0.3),圖7 中的計算結果顯示:在典型螺旋波等離子體電子溫度條件下,由于螺旋波與TG 波的橫向波數不相等,故有限拉莫爾半徑效應因子存在兩個不同的分支,螺旋波對應的螺旋模分支(H-mode branch)和TG 波對應的TG 模分支(TG-mode branch);當歸一化頻率ω/ωce逐漸增大(即靜磁場B0逐漸減小)時,螺旋波與TG 波開始靠近模式耦合層,即兩種波的橫向波數逐漸相等,這表現為兩個有限拉莫爾半徑效應因子分支開始合二為一.值得注意的是,在典型低磁場條件下,例如B0=48 Gs (ω/ωce=0.1)時,TG 波對應的有限拉莫爾半徑效應因子λe≈0.025,且隨著縱向靜磁場的減小,λe進一步變大,這說明在低磁場條件下,在計算波功率沉積過程中,必須考慮有限拉莫爾半徑效應的影響.

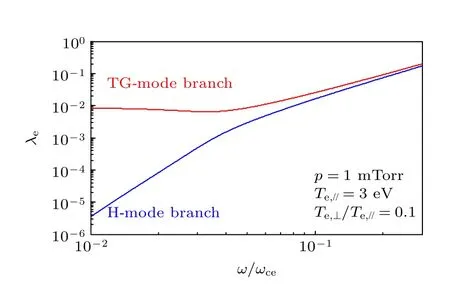
圖7 螺旋波與TG 波有限拉莫爾半徑效應因子隨歸一化靜磁場的變化關系Fig.7.Dependence of the FLR effect parameter of helicon and TG waves on the normalized static magnetic field.

聯合圖4 和圖5 結果可知,隨著縱向靜磁場的減小,n=1 次回旋諧波在B0≈48 Gs 處最先遭遇回旋阻尼,忽略n≥2 次回旋諧波在阻尼計算中的貢獻,因為它們在更低的靜磁場值處出現回旋阻尼,而這些更低的靜磁場情形不屬于本文的討論范圍.基于此,在考慮有限拉莫爾半徑效應和n≤1次回旋諧波的情形下,在n0=1×1013cm-3,B0=48 Gs,p=1 mTorr,Te,⊥/Te,//=0.1,v0,?/vth?,//=0.1參量條件下,圖8 所示為螺旋波與TG 波碰撞阻尼、朗道阻尼及回旋阻尼產生的功率沉積隨縱向電子溫度的變化關系.由圖8 可知: 在當前低磁場條件下,螺旋波與TG 波碰撞阻尼產生的功率沉積在典型螺旋波等離子體電子溫度范圍內扮演主導作用,特別是 TG 波碰撞阻尼產生的功率沉積占據主導地位;而由朗道阻尼及回旋阻尼產生的波功率沉積完全可以忽略.這是因為在當前低磁場情形下,產生朗道阻尼的波相速和電子熱速度之間的共振效應不明顯,同時,由波頻率、電子回旋頻率及電子熱速度之間的共振效應產生的回旋阻尼亦不是主要的波能量沉積機制,此時碰撞阻尼機制成為波能量沉積的主要方式;另一方面,在當前低磁場(B0=48 Gs)條件下,由于TG 波可滲入等離子體內部傳播,電子在其電場中加速后通過碰撞效應將電磁波能量傳遞給等離子體.

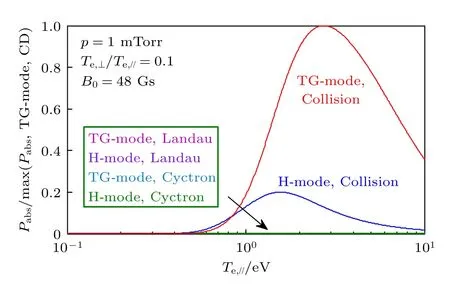
圖8 波功率沉積隨縱向電子溫度的變化Fig.8.Wave power deposition versus parallel electron temperature.

為更詳細分析螺旋波與TG 波碰撞阻尼產生的功率沉積特性,在n0=1×1012cm-3,B0=48 Gs,Te,//=5 eV,p=1 mTorr,v0,?/vth?,//=0.1參量條件下,圖9 和圖10 分別為低磁場條件下螺旋波和TG 波碰撞阻尼產生的功率沉積對電子溫度各向異性因子的依賴關系.對于螺旋波,從圖9可以看出,隨著電子橫向溫度的增大,螺旋波碰撞阻尼產生的功率沉積更加聚焦在等離子體柱中心區域.而對于TG 波,圖10 表明其由碰撞阻尼產生的功率沉積特性對電子溫度各向異性的依賴關系較為復雜,在電子溫度各向同性(Te,⊥/Te,//=1)條件下,功率沉積在某些半徑值處取得較大值,在中心處出現峰值;而在電子溫度各向異性情況下,當電子橫向溫度小于縱向溫度(Te,⊥/Te,//=0.1)時,功率沉積在某些半徑值處的強度減弱,當電子橫向溫度大于縱向溫度(Te,⊥/Te,//=10)時,功率沉積在某些半徑值處的強度變得可以忽略,功率沉積聚焦在中心處很小的半徑范圍內.這些結果說明電子溫度各向異性對螺旋波和TG 波的功率沉積的影響并不相同,這可能是由于兩種波的傳播特性不同而致,螺旋波作為一種平行于外界靜磁場方向傳播的右手圓極化波,粒子溫度各向異性對其傳播影響較小;而TG 波本質上是一種傾斜于外界靜磁場方向傳播的準靜電波,其對粒子溫度參量空間分布的變化較為明顯.這為深入研究螺旋波等離子體中由參量不穩定引起的湍流加熱現象提供了切入點.

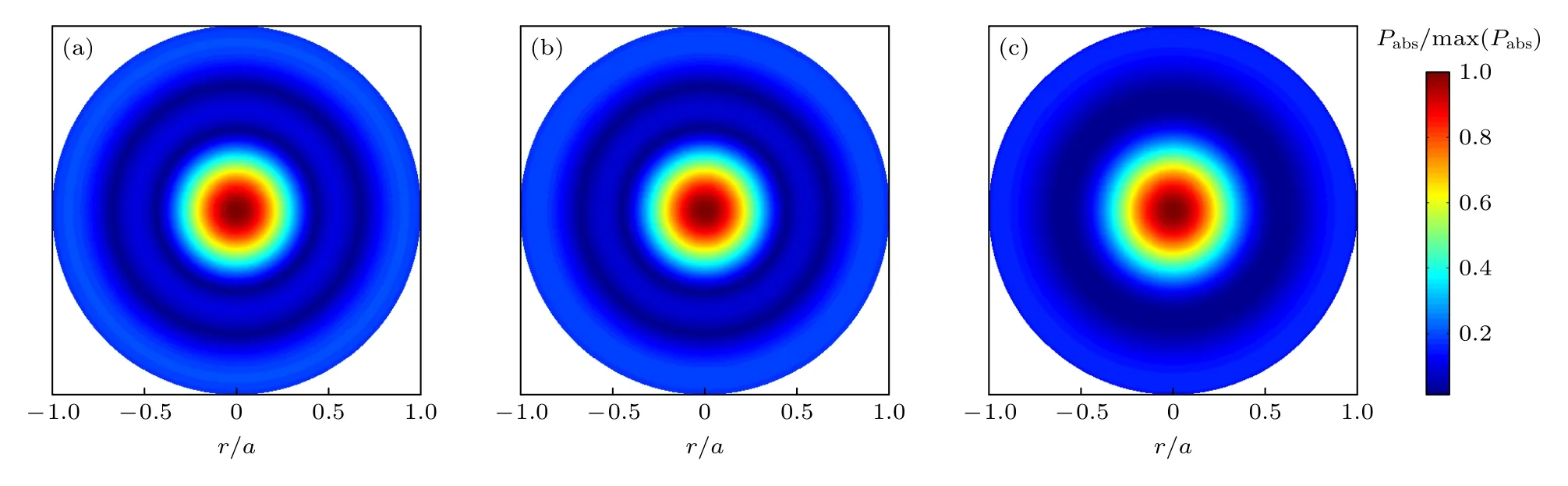
圖9 螺旋波碰撞阻尼產生的功率沉積徑向分布 (a) Te,⊥/Te,//=0.1;(b) Te,⊥/Te,//=1;(c) Te,⊥/Te,//=10Fig.9.Collisional damping induced radial power deposition distribution of the helicon wave: (a) Te,⊥/Te,//=0.1;(b) Te,⊥/Te,//=1;(c) Te,⊥/ Te,//=10.

圖10 TG 波碰撞阻尼產生的功率沉積徑向分布 (a) Te,⊥/Te,//=0.1;(b) Te,⊥/Te,//=1;(c) Te,⊥/Te,//=10Fig.10.Collisional damping induced radial power deposition distribution of the TG wave: (a) Te,⊥/Te,//=0.1;(b) Te,⊥/Te,//=1;(c) Te,⊥/Te,//=10.

基于以上分析,可以看出在低磁場、低氣壓條件下,TG 波在功率沉積中占有主導地位,為分析電子縱向溫度Te,//和電子溫度各向異性因子Te,⊥/Te,//對TG 波功率沉積的影響,在n0=1×1012cm-3,B0=60 Gs,p=1 mTorr,v0l/vthl,//=0.1參量條件下,圖11 給出了TG 波功率沉積在(Te,//,Te,⊥/Te,//)變量區間的分布特性.由圖11 可知,隨著電子縱向溫度Te,//的增大,功率沉積逐漸增大,在Te,//≈10 eV 處功率沉積出現峰值;另一方面,當電子縱向溫度Te,//≈10 eV 給定,隨著電子橫向溫度Te,⊥逐漸減小,功率沉積逐漸增強.這表明電子縱向溫度和電子溫度各向異性因子兩者共同決定了TG 波的功率沉積特性;在變量空間(Te,//,Te,⊥/Te,//),存在某一臨界點,在此臨界點,TG 波的功率沉積取得峰值.這一臨界點的位置是碰撞阻尼、朗道阻尼及回旋阻尼這3 種阻尼共同作用的結果;而功率沉積的峰值的大小,則取決于3 種阻尼在波功率沉積中各自占的比重,以及哪種波在主導功率沉積.

圖11 TG 波功率沉積在 (Te,//,Te,⊥/Te,//) 空間的分布 (a) 三維分布;(b) 二維分布Fig.11.(Te,//,Te,⊥/Te,//) space power deposition distribution of TG wave: (a) 3D;(b) 2D.

4 結論

在磁化、均勻密度分布螺旋波等離子體中,考慮粒子熱效應、縱向漂移速度及溫度各向異性情形下,理論分析了螺旋波等離子體典型參量條件下Whistler 波的傳播特性及低磁場、低氣壓條件下螺旋波與Trivelpiece-Gould 波的功率沉積特性.1)在電子溫度各向同性情形下,不同回旋諧波的衰減常數在不同縱向靜磁場閾值處開始顯著單調增大,而相位常數則在初始即顯著陡升;在電子溫度各向異性情形下,不同諧波衰減常數顯著增大時對應的縱向靜磁場閾值變小,且衰減常數和相位常數不再單調變化,均存在峰值現象,衰減常數顯著陡升和相位常數出現峰值兩個現象步調一致.這是因為粒子溫度各向異性徹底改變了波-粒互作用過程,在橫向、縱向不同方向上主導波-粒互作用過程的回旋阻尼、朗道阻尼及碰撞阻尼,共同決定電磁波在給定參量條件下所遭受的阻尼強度.2)隨著電子橫向溫度的增大,波遭受顯著阻尼對應的縱向靜磁場閾值變大,而波遭受的阻尼強度變小.這是由于隨著電子橫向熱速度的增大,波-粒共振效應所需的回旋磁場強度也應增大,但回旋阻尼本身并不一定能夠主導整個功率沉積過程.3)考慮電子有限拉莫爾半徑效應,在低磁場、低氣壓條件下,分析結果表明TG 波碰撞阻尼產生的功率沉積在典型螺旋波等離子體電子溫度范圍內占據主導地位;且存在某一臨界電子縱向溫度值,使得在此臨界值處TG 波的功率沉積出現最大值,隨著電子橫向溫度的減小,TG 波的功率沉積峰值逐步增大,這說明相比縱向的碰撞阻尼和朗道阻尼產生的功率,回旋阻尼產生的功率沉積可以忽略.這可能是因為TG 波作為一種電子回旋波,其在當前低磁場情形下主要通過碰撞效應將波的能量傳遞給粒子.這些結論為揭示螺旋波等離子體高密度特性背后的物理機制提供了重要的理論線索.