二元氧化物Yb3TaO7 的非晶狀熱傳導機理*

王學智 湯雨婷 車軍偉 令狐佳珺 侯兆陽

1) (長安大學理學院應用物理系,西安 710064)

2) (湖南大學機械與運載工程學院,汽車車身先進設計制造國家重點實驗室,長沙 410082)

3) (西安交通大學物理學院,教育部物質非平衡合成與調控重點實驗室,西安 710049)

具有非晶狀熱導率的固體材料在熱能轉換和熱管理應用中備受青睞.因此,揭示晶體材料的非晶狀熱傳導機理對于開發和設計低熱導率材料至關重要.本文運用原子模擬方法揭示了螢石結構二元簡單晶體Yb3TaO7 的非晶狀低熱導率的物理機理.研究發現,螢石Yb3TaO7 的低熱導率主要是由O-Yb 和O-Ta 之間的原子間結合力相差較大引起的.這種相差較大的原子鍵可以極大地軟化聲子模式,從而抑制聲子輸運.振動模式分解顯示,螢石Yb3TaO7 中的大多數聲子模式位于Ioffe-Regel 極限以下,表現出強烈的擴散特征.螢石Yb3TaO7 中絕大部分(＞ 90%)的熱流是通過擴散模式而不是傳播模式傳輸.因此,螢石Yb3TaO7 中的熱傳導表現出獨特的類非晶特性.同時發現,螢石Yb3TaO7 中的光學聲子模式在熱傳導中發揮著重要的作用.本文對于原子間結合力與低熱導率之間關系的認識,以及開發和設計低熱導率材料提供了新思路.

1 引言

熱障涂層(TBC)廣泛應用于航空發動機和燃氣輪機的高溫熱端部件表面,以防止部件被高溫腐蝕并提高熱效率和服役壽命[1].隨著航空發動機和燃氣輪機向更高溫度和高推重比發展,其內部溫度也越來越高.因此,開發和設計具有超低熱導率的TBC 材料是提高航空發動機和燃氣輪機高溫服役性能的有效途徑.由于TBC 材料為絕緣體,熱能在TBC 材料中主要以晶格振動(聲子)為熱載體進行傳導[2].目前,基于聲子的缺陷工程和高熵工程是降低材料固有熱導率的兩種主要方式.通過缺陷工程在基體材料中引入缺陷可顯著阻礙聲子輸運,進而降低材料的熱導率.例如,Y2O3穩定的ZrO2(YSZ) 中的大量氧空位有效地降低了ZrO2的熱導率,甚至當Y2O3的摩爾質量摻雜比為12%時出現了非晶熱傳導現象[3].利用高熵工程在基體中引入外來原子增加材料的結構復雜性亦可使聲子發生“瑞利散射”,進而獲得低熱導率.Zhu 等[4]報道了高熵TBC 材料(La0.2Nd0.2Y0.2Er0.2Yb0.2)2Zr2O7和(La0.2Nd0.2Sm0.2Gd0.2Yb0.2)2Zr2O7具有類似非晶的超低熱導率.雖然缺陷和高熵工程可有效地減少熱導率,但它們也帶來一些科學和工程上的挑戰.例如,當Y2O3的摩爾質量摻雜比超過12%時,YSZ 的熱導率將達到極限[3].同時,過多的氧空位又會降低YSZ 的力學穩定性和斷裂韌性[5].同樣,高熵工程法會提高成本以及技術復雜性.例如,利用物理氣相沉積(PVD)或等離子體噴霧(PS)制備高熵涂層的過程中,由于各元素的蒸發度不同,所獲得試樣的成分通常會偏離所需的成分,甚至有可能無法制備出所需的試樣[6].因此,在簡單體系的材料中實現低熱導率就顯得非常重要.

相對于晶體材料,完全無序或非晶材料具有非常低的熱導率[7].稀土鉭酸鹽Yb3TaO7通常具有兩種晶體結構,即無序的螢石結構(fluorite,F)和有序的冰鎂石結構(weberite,W)[8].近年來,螢石結構的Yb3TaO7成為一種重要的TBC 材料,并且由于其低熱導率和優異的相位穩定性而引起了研究人員極大的興趣[9].有趣的是,盡管這種晶體材料成分簡單,卻擁有反常的非晶狀熱傳導特性.然而,目前對這種低熱導率的微觀機理仍不清晰.特別是,對其表現出的非晶狀熱傳導的機理還缺乏深入理解.揭示這些機制有利于低熱導率材料的開發和設計.另一方面,實驗測得的熱導率通常因試樣密度和熱輻射的存在而變化[10,11].因此,僅依靠實驗手段研究螢石Yb3TaO7在更廣泛溫度范圍內的固有熱輸運性質是具有挑戰性的.為此,采用原子模擬來研究Yb3TaO7的固有熱導率及其機理.

在本文中,首先利用分子動力學(MD)計算了Yb3TaO7在300—1500 K 溫度范圍內的熱導率.接著,利用聲子譜能量密度和晶格動力學揭示了Yb3TaO7中的聲子模式.最后,利用雙通道聲子模型定量計算了Yb3TaO7中各聲子模式對熱導率的貢獻.研究發現,波動的原子間相互作用所驅動的擴散聲子模式導致簡單成分的螢石Yb3TaO7表現出類似非晶的低熱導率.該研究表明,可以通過增大化學鍵之間的差異性來軟化聲子模式,進而可在簡單材料中實現低熱導率.

2 計算方法

圖1 所展示的是螢石型和冰鎂石型Yb3TaO7的晶體結構.對于螢石型Yb3TaO7,其晶體結構的空間群為Fm3m,Yb 和Ta 原子隨機占據4a(0,0,0)位點,氧原子和1/8 的氧空位隨機占據8c(1/4,1/4,1/4)位點.對于冰鎂石型Yb3TaO7,其晶體結構的空間群為C2221,Yb 原子占據4b(0,1/2,0) 和8g(x,y,1/2)位點,Ta 原子占據4a(0,0,0)位點,O 原子占據4c(1/2,y,1/4),16h(x,y,z)和8g(x,y,1/4)位點.本文中的Yb3TaO7超胞模型包含8×8×8 個原胞,共有6144 個原子.

圖1 Yb3TaO7 (a) 螢石結構;(b)冰鎂石結構Fig.1.Yb3TaO7: (a) Fluorite-type;(b) weberite-type.

Yb3TaO7的原子間相互作用以基于剛體的波恩模型描述,其表達式為

其中第一項是長程庫侖勢能,后面兩項為短程排斥勢能.ε0為真空介電常數,rij表示第i個原子和第j個原子之間的距離,qi和qj表示相應的電荷,Aij,ρij和Cij是可調參數,如表1 所列.同時,采用精度為1.0×10—6的Ewald 近似算法來計算長程庫侖勢.所有的計算都是通過LAMMPS 軟件來實現,其中在三維空間的每個方向都是周期性邊界,并利用Nose-Hoover 熱浴法來控制體系的溫度和壓力.

表1 Yb3TaO7 的力場參數[12,13]Table 1.Force field parameters for Yb3TaO7[12,13].

Yb3TaO7的熱導率(κ)由基于波動耗散理論的平衡分子動力學(equilibrium molecular dynamics,EMD)計算而來,具體表達式如Green-Kubo (G-K)公式所示[14]:

其中kB表示玻爾茲曼常數;T表示溫度;V表示模擬體系的體積,〈 J(0)·J(t)〉 表示熱流自相關函數(heat current autocorrelation function,HCACF).EMD-GK 方法可消除模擬體系的尺寸效應,即得到材料的固有熱導率.熱電流J計算表達式為

其中υi,ri,mi,vi和Ui分別表示第i個原子的速度、位置、質量、位力和勢能.本文對體系進行了10 次獨立計算以計算出平均熱導率和誤差.

本文采用聲子譜能量密度(spectral energy density,SED)法計算Yb3TaO7的聲子色散關系.該方法直接將原子的振動軌跡投影到振動模式上,以確定振動能量在波矢-頻率空間的分布[15-18]:

晶格振動模式(聲子)的分析基于經典晶格動力學(lattice dynamics,LD)展開[19]:

其中uiλα表示質量為mi的原子在α方向的振動位移;eλ,iα表示聲子本征矢量;ωλ表示模式λ的聲子本征值(頻率);t表示時間.為了獲得本征值ωλ,需求解波動方程:

其中D表示動力學矩陣.D可根據下式計算而來:

式中,Ep表示總勢能.

3 結果與討論

3.1 熱導率

為了對比研究,本文以冰鎂石結構的Yb3TaO7為參照物.在計算熱導率前,首先需要對模型和力場的可靠性進行驗證.為此,將晶格常數、格林艾森常數和彈性模量的計算值與文獻報道的實驗值[8]進行了對比,如表2 所列.從表2 可以看出,晶格常數的計算值與實驗值非常吻合,故本文的力場參數可以正確描述Yb3TaO7的晶體結構.格林艾森常數可以定量地描述固體材料中聲子間的非簡諧相互作用強度[20],故可用來驗證力場描述聲子的可靠性.此外,格林艾森常數的計算值與實驗值也相當吻合.最后,對比了彈性模量,因為彈性模量也與聲子熱輸運有關.從表2 還可以看出,彈性模量的計算值與實驗值吻合較好.總之,通過對比Yb3TaO7的結構參數和熱力學性質的計算值與實驗值,證實了我們所采用力場的可靠性.

表2 計算的La2Zr2O7 和Yb3TaO7 的晶格常數、格林艾森常數和彈性模量Table 2.Calculated lattice constants,Grüneisen constants,and elastic modulus for La2Zr2O7 and Yb3TaO7.

基于驗證的原子模型和力場,利用EMD-GK法計算了熱導率.為了獲得Yb3TaO7的固有熱導率,需要對模擬時間進行驗證.圖2(a)和圖2(b)顯示的是螢石Yb3TaO7在1500 K 下的HCACF 和熱導率隨關聯時間的變化關系.從圖2(a)和圖2(b)中可以看出,HCACF 隨著關聯時間的增加而迅速衰減,同時熱導率趨于收斂,這與波動-耗散理論是一致的.因此,本文中使用的20 ps 的關聯時間足以獲得收斂的熱導率.接著,研究了超胞的大小對計算熱導率的影響,如圖2(c)所示.從圖2(c)可以看出,熱導率隨著超胞的大小的增加依然保持收斂,這是因為本文中選取的超胞尺寸遠大于聲子平均自由程(phonon mean free path,PMFP)(0.41—0.33 nm).該結果同時與EMD-GK 方法可以消除尺寸效應的原則是一致的.總之,上述結果說明本研究中選擇的模擬時間和超胞尺寸足以獲得固有的熱導率.

圖2 1500 K 溫度下的熱導率計算結果 (a) 歸一化熱流關聯函數隨關聯時間的變化關系;(b) 熱導率隨關聯時間的變化關系;(c) 不同超胞的熱導率;(d) 熱導率隨溫度的變化關系Fig.2.Calculated thermal conductivity at 1500 K: (a) Normalized HCACF versus correlation time;(2) thermal conductivity versus correlation time;(c) calculated thermal conductivity with different supercell;(d) temperature dependence of thermal conductivity.

圖2(d)顯示的是螢石型和冰鎂石型Yb3TaO7在300—1500 K 的溫度范圍內熱導率的計算結果.同時,將熱導率的計算結果與文獻報道的實驗結果進行了對比.從圖2(d)可以看出,螢石型Yb3TaO7的熱導率的計算結果與實驗結果非常吻合,但目前還沒有冰鎂石型Yb3TaO7的熱導率的實驗報道.計算結果表明,螢石型Yb3TaO7的熱導率隨溫度的增大而增大,表現出反常的非晶熱傳導特征.相反,冰鎂石型Yb3TaO7的熱導率隨溫度的增大而減小,表現出經典的晶體熱傳導特征.熱導率對溫度的依賴關系可定量地描述為

其中A,B和n是材料參數.根據(8)式,螢石結構和冰鎂石結構的n值分別為—0.08 和1.032.更重要的是,在低溫下,螢石結構的熱導率遠低于冰鎂石結構的熱導率.上述結果表明,螢石型二元氧化物Yb3TaO7具有類非晶的低熱導率.因此,揭示這一現象背后的機理對于開發和設計低熱導率的材料具有重要的意義.

3.2 聲子散射

盡管EMD-GK 計算給出了和實驗值相一致的熱導率,但它并沒給出關于聲子層面的機理描述.聲子氣模型(PGM)是理解微納尺度熱輸運的經典模型[21].假設晶體螢石Yb3TaO7中所有聲子模式都是正常模式,即聲子有明確的波矢和周期性的本征矢量(速度場).基于PGM,螢石Yb3TaO7的微觀熱傳導可描述為

其中V是晶胞體積;C(ωλ)是模式比熱容;υg(ωλ)是聲子群速度;τ(ωλ)是聲子壽命(弛豫時間).C(ωλ)由玻色-愛因斯坦統計學計算:

其中 ? 是約化普朗克常數.基于聲子色散關系,群速度υg可根據公式υg=?ω/? q計算而來.利用洛倫茲函數擬合SED 可計算出聲子壽命τ(ωλ)[15]:

其中I表示SED 的峰值;ωc表示峰中心對應的頻率;γ表示SED 峰的半高寬(HWHM).據此,聲子壽命可表示為τλ=1/2γ.以300 K 為例,圖3 顯示的是螢石Yb3TaO7的模式比熱容、聲子群速度和聲子壽命的計算結果.基于PGM,Yb3TaO7的熱導率為0.36 W·m—1·K—1,該值遠小于EMD-GK 值(1.25 W·m—1·K—1)以及實驗值(1.10 W·m—1·K—1).如此大的差異表明,基于PGM 的單通道模型無法準確描述螢石Yb3TaO7的聲子熱傳導性質.事實上,這并不是PGM 第一次在描述聲子熱傳導時失效.例如,PGM 無法準確處理超晶格[22]和聲子晶體中的相干聲子[23],也無法處理La2Zr2O7[24]和α-DX[25]中的擴散聲子.上述結果意味著螢石Yb3TaO7中包含不明確的聲子模式,而這些模式無法用PGM描述.

圖3 在300 K 溫度下,螢石Yb3TaO7 的熱輸運性質 (a) 模式比熱容;(b) 聲子壽命;(c)聲子群速度Fig.3.Thermal transport properties of F-Yb3TaO7 at 300 K: (a) Mode capacity;(b) phonon lifetime;(c) phonon group velocity.

基于此,利用SED 考察了聲子色散關系,如圖4所示.從圖4 可以看出,螢石Yb3TaO7的色散關系只有在1.5 THz 以下的聲學支部分是清晰的,而高頻光學模式有很大的聲子線寬且色散曲線極其模糊.相比于螢石Yb3TaO7,冰鎂石Yb3TaO7的聲子色散關系就顯得相對清晰明確.接著,將SED投影到頻率空間,每個峰對應一支色散關系,其峰寬和聲子散射率有關.從圖4 可以看到,螢石Yb3TaO7的SED 峰在低頻時較尖銳,而在高頻時則明顯變寬,說明螢石Yb3TaO7中存在很強的聲子散射.然而,冰鎂石Yb3TaO7的SED 峰相比于螢石Yb3TaO7更尖銳,該結果與其相對清晰的色散關系相一致.同時可以看到,螢石Yb3TaO7的SED 峰值遠小于冰鎂石Yb3TaO7的SED 峰值,說明螢石Yb3TaO7中的聲子模式具有非常低的振動能量和傳熱率,進而表現為低熱導率.綜上,SED 分析表明,螢石Yb3TaO7由于強聲子散射而包含非正常的聲子模式.

圖4 Yb3TaO7 的SED 計算結果 (a) 螢石;(b) 冰鎂石Fig.4.Calculated SED plots of Yb3TaO7: (a) F-type;(b) W-type.

螢石型和冰鎂石型的Yb3TaO7具有完全相同的元素成份和氧空位濃度,故離子半徑差、離子質量差和氧空位無法解釋螢石型Yb3TaO7的強聲子散射.聲子是晶格的集體振動,故強聲子散射可能和原子間相互作用有關.目前,還沒有可以定量地描述聲子散射率和原子間相互作用的理論.因此,分別計算了螢石型和冰鎂石型Yb3TaO7的原子間相互作用力,以給出定性解釋.如圖5(a)所示,螢石型Yb3TaO7中O-Ta 和O-Yb 之間的結合力差值遠大于冰鎂石結構中的差值,即螢石型Yb3TaO7的原子間相互作用是高度不均勻的.為了解釋這種不均勻相互作用力對聲子的散射,以一維雙原子鏈為例.一維雙原子鏈的聲子色散關系為

圖5 (a) 原子間相互作用力;(b) 一維雙原子鏈的聲子色散關系Fig.5.(a) Calculated interatomic bonding force;(b) phonon dispersion relationship of for a one-dimensional diatomic chain.

其中M和m為相鄰原子的質量;G和g為相應的力常數(詳細推導過程請見補充材料).如圖5(b)所示,隨著力常數G和g之間差異的增大,聲子模式變得軟化,聲子群速度降低,表明聲子散射增強.因此,螢石型Yb3TaO7的強聲子散射是由其高度不均勻的原子間相互作用所導致.

3.3 聲子模式

上述內容揭示了螢石Yb3TaO7中存在非正常的聲子模式及其原因.為了直觀地理解這些聲子模式,將聲子本征矢量歸一化到單位極化球上[3]:

其中eiα,λ表示第i個原子在模式λ中α方向的本征矢量;e* 為共軛本征矢量.如果一個給定的聲子模式λ是正常的聲子模式,即它具有類似于平面波的周期性波矢和本征矢量,那么它的極化矢量將聚焦于極化球表面.這種正常的模式即傳播模式,也叫作傳播子(propagons).如果極化矢量隨機地散布在極化球表面,那么這種模式是不明確的,對應于局域化模式和擴散模式,也叫作局域子(locons)和擴散子(diffusons).如圖6 所示,當頻率范圍小于1.0 THz 時,螢石和冰鎂石型Yb3TaO7的聲子極化均聚焦于球面上點,這對應于具有明確色散關系的聲學模式.當頻率范圍擴大到2.5 THz時,螢石結構的聲子極化開始隨機分布在球面上,聲子本征矢量的極化表現出明顯的局域化特點.然而,冰鎂石結構的聲子極化仍聚焦于球面,且可以分辨.螢石結構中隨機分布的模式對應于非正常模式.最后,我們將頻率范圍擴大到25 THz.從圖6可以看出,螢石結構中絕大多數的聲子極化隨機分布于球面而無法區分,而冰鎂石結構的大量聲子聚焦于極化球的赤道區域.這一顯著差異是因為螢石結構的原子間相互作用是高度不均勻的,而冰鎂石結構的原子間相互作用是相對均勻的.總之,聲子本征矢量的極化分析直觀地證實了Yb3TaO7同時具有局域化和非局域化的聲子模式.

圖6 Yb3TaO7 在不同頻率區間內的聲子極化 (a) 螢石;(b) 冰鎂石Fig.6.Phonon polarization of Yb3TaO7 in different frequency domains: (a) F-type;(b) W-type.

接下來,對整個聲子譜進行了模式分解,以精確確定局域子、傳播子和擴散子的分布區間.局域子可直接通過聲子參與率(participation ratio,PR)來確定[26]:

其中N是體系的總原子數.PR 定量地衡量了體系中有多少原子對給定的聲子模式λ有貢獻.一般地,如果PR ＜ 0.1,則該模式是局域子.如圖7(a)和圖7(b)所示,螢石Yb3TaO7在高頻有大量的局域子,而冰鎂石Yb3TaO7在低頻和高頻均存在少量的局域子.這些局域子是局域化的振動模式,對熱傳導的貢獻可以忽略不計.同時可以看到,螢石結構的聲子PR 小于冰鎂石結構的聲子PR,說明非均勻的原子間相互作用抑制了聲子模式的激發.總的聲子PR 可以進一步投影到各原子上,以確定不同的原子對聲子模式的貢獻:

如圖7(c)所示,螢石Yb3TaO7低于7 THz 的低頻聲子主要來源于Yb 原子的振動,高于7 THz的高頻聲子主要來源于O 原子的振動,而Yb 的振動對聲子的貢獻相當小.此外,Ta 原子的PR 在7 THz 處達到最大值,而Yb 原子的PR 在4 THz處達到最大值.這一差異可歸因于O-Ta 的原子間結合力遠大于O-Yb 的原子間結合力.如圖7(d)所示,冰鎂石Yb3TaO7低于7 THz 的低頻聲子也主要來源于Yb 原子的振動,介于7—8 THz 的聲子主要來源于Ta 原子的振動,高于8 THz 的聲子則主要來源于O 原子的振動.與螢石Yb3TaO7不同的是,冰鎂石Yb3TaO7中Ta 原子對聲子的貢獻明顯較大.

圖7 (a) 螢石Yb3TaO7 和(b) 冰鎂石Yb3TaO7 的總參與率;(c) 螢石Yb3TaO7 和(d) 冰鎂石Yb3TaO7 中各元素的參與率Fig.7.Total phonon participation ratio of (a) F-Yb3TaO7 and (b) W-Yb3TaO7;atomic phonon participation ratio of (c) F-Yb3TaO7 and (d) W-Yb3TaO7.

傳播子和擴散子可利用Ioffe-Regel 準則區分[27].根據該準則,若給定聲子的平均自由程(MFP)大于體系的原子間最小距離,則該聲子是傳播子,否則是擴散子.如圖8 所示,螢石Yb3TaO7中 90%的聲子模式落在Ioffe-Regel 區間,表現出擴散子特征.然而,冰鎂石Yb3TaO7存在大量的傳播子.此外,通過對比可發現,螢石Yb3TaO7中聲子的MFP 整體上遠小于冰鎂石Yb3TaO7,這說明高度不均勻的原子間相互作用導致螢石Yb3TaO7的聲子表現出強烈的擴散特征.

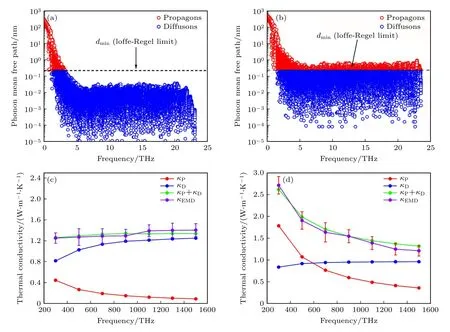
圖8 Yb3TaO7 的聲子平均自由程 (a) 螢石,(b)冰鎂石;Yb3TaO7 中傳播子和擴散子的熱導率 (c) 螢石,(d) 冰鎂石Fig.8.Phonon mean free paths of (a) F-Yb3TaO7 and (b) F-Yb3TaO7;thermal conductivity of propagons and diffusons in (c) FYb3TaO7 and (d) F-Yb3TaO7.

上述模式分解表明,熱能在Yb3TaO7中是由傳播子和擴散子傳導的.為了定量地描述傳播子和擴散子對熱導率的貢獻,我們對熱導率進行了譜分解.如前所述,傳播子具有周期性的波矢和本征矢量,其對熱導率的貢獻(κP)可根據(9)式計算.擴散子無周期性的波矢和本征矢量,且以隨機擴散的方式進行熱傳導,故擴散子對熱導率的貢獻(κD)可根據Allen-Feldman (A-F)擴散理論計算[28]:

式中,D(ωλ)是聲子模式λ的擴散率:

(15)式中的S λλ′是非對角化的熱流矩陣:

其中Q為布里淵區內的波矢量之和;λ和λ′代表不同的聲子模式.Θ Qλλ′可根據晶格動力學矩陣計算:

式中,e是聲子本征矢量;α和β表示笛卡爾方向;Rs表示周期性超胞內每個單胞(標記為s)相對原胞(標記為0)的位移矢量;表示單胞內原子k相對原子k′的位移矢量,是根據(7)式計算的動力學矩陣.圖8(a)和圖8(b)展示的是螢石型和冰鎂石型Yb3TaO7的模式熱導率.從圖8(a)和圖8(b)中可看出,螢石Yb3TaO7的熱導率主要由擴散子貢獻,故螢石Yb3TaO7的熱導率整體表現出非晶熱傳導特性.雖然當溫度高于500 K時,冰鎂石Yb3TaO7的熱導率主要由擴散子貢獻,但熱導率隨溫度的變化關系仍由傳播子主導,故冰鎂石Yb3TaO7的熱導率表現出晶體熱傳導特性.

綜上,PR 和Ioffe-Regel 準則準確給出了螢石Yb3TaO7的局域子、傳播子和擴散子的分布.因此,在Yb3TaO7中存在雙通道聲子熱傳導現象.熱傳導的模式分解表明,螢石Yb3TaO7的熱導率主要是由高頻的擴散子貢獻的.為了預測或計算材料的熱導率,目前已經建立了一些簡化的物理模型,即通過一些簡單的物理參數即可得到材料的熱導率,且這些模型大都建立在高頻光學聲子對熱導率可忽略的假設上[29-32].然而,本文中螢石Yb3TaO7的結果證實,高頻的光學聲子在熱傳導中起著不可忽視甚至是決定性的作用.這一結果為調控熱傳導提供了新視角.

4 結論

本文從原子間結合和晶格振動模式的角度出發,研究了螢石Yb3TaO7晶體的非晶狀熱傳導機理.螢石Yb3TaO7的低熱導率主要是由O-Ta 和O-Yb 之間較大的差異驅動的軟化聲子導致的.由于存在大量的擴散振動模式,基于PGM 的單通道模型無法合理描述螢石Yb3TaO7的熱傳導.振動模式分解發現,螢石Yb3TaO7中的絕大部分熱量是由擴散模式傳輸的,導致其熱傳導具有類似非晶的特性.同時發現,螢石Yb3TaO7中的光學聲子模式在熱傳導中具有重要的作用,這可為調控熱傳導提供新的物理維度.該研究啟發我們,增強化學鍵的不均勻性可以激發更多的擴散振動模式,從而有利于在簡單材料中實現非常低的熱導率.