基于深度學習的快速車道線檢測方法

劉 彬，魏為民

（上海電力大學 計算機科學與技術學院，上海 201306）

車道線檢測是自動駕駛的基礎技術之一，其檢測的準確率和效率直接影響著自動駕駛的性能。車道線檢測技術作為當前自動駕駛[1]領域尚未完全解決的問題之一，仍然具有較高的難度和挑戰性。

目前對車道線檢測的研究主要分為兩種，分別是基于傳統的圖像處理方法和基于深度學習的方法。

傳統的圖像處理方法[2-4]往往通過Canny邊緣檢測、Hough變換、最小二乘法等技術擬合出車道線，該方法具有實時性強、準確率高的特點。但對于能見度較低的路況，比如雨雪天氣，其檢測準確率將大大下降。

對于基于圖像分割的方法，PINet[5]模型提出了在車道線檢測時基于關鍵點信息，從而實現使用較少的參數便可以檢測不同數量，不同方向的車道線；HOU等[6]提出自注意力蒸餾算法（Self Attention Distillation, SAD），該使用語義分割及知識蒸餾的方式，增強了卷積神經網絡的特征表達能力，從而使分割效果得到了大幅提升；胡序洋等[7]提出了基于LaneSegNet網絡的檢測方法，其綜合使用了基于編解碼的原理構建Lane-Net、多尺度空洞卷積和混合注意力機制實現了對車道線的提取；何春明等[8]提出了空間卷積神經網絡（Spa- tial CNN, SCNN）模型，基于模糊熵的灰度局部熵（Gray Level and Local Entropy, GLLE）熵閾值分割方法，相較于傳統的圖像分割方法，該方法得到更加準確的閾值，提高了分割精度。這類基于圖像分割的方法在檢測準確度上有著明顯的優勢，但是在車道線提取速度上很難達到要求（+30 FPS）。

車道線檢測速度慢、精度差是目前以深度學習為基礎的車道線檢測方法普遍存在的問題。針對這些問題，本文新提出了LaneBezierNet，一種端到端的車道標線檢測的卷積神經網絡。如圖1所示，該算法從安裝在車輛前端的攝像頭得到圖像后，經過LaneBezierNet直接輸出表示圖像中每條車道線的貝塞爾曲線控制點，不需要任何后處理來進行車道估計。

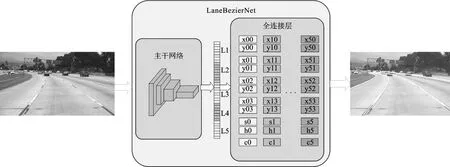
圖1 LaneBezierNet工作流程

1 相關工作

1.1 LaneBezierNet

本文中使用3階貝塞爾曲線作為回歸方程式，如圖2所示，獲取圖像后先對圖像進行數據增強，然后將處理后的數據作為主干網絡的輸入，并在主干網絡后加入一層全連接層，全連接層的輸出包含了貝塞爾曲線的控制點坐標，通過這些控制點的坐標信息便可得到整條車道線的數據。LUCAS等[9]提出的基于多項式回歸的方法，將每條車道線看作一條3階或更高階的多項式，比如y=ax3+bx2+cx+d。但是對于一些曲率較大的道路并不能很好地找到一條多項式曲線與之對應。本文則是將每條車道線視為一條貝塞爾曲線，實驗結果表明3階貝塞爾曲線便可準確的描述各類車道線信息。

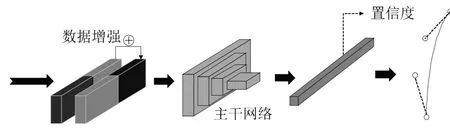
圖2 LaneBezierNet算法流程圖

1.2 數據增強

為了提高算法的泛化能力，本方法在將圖像傳給主干網絡之前加入了數據增強模塊，其中包括10°的隨機旋轉、隨機水平翻轉和隨機裁剪，如圖3所示。

圖3 數據增強

1.3 貝塞爾曲線

貝塞爾曲線是一種被大量應用于圖形繪制的曲線。該曲線是由節點、節點與節點之間的線段組成，使用它可以精確地繪制出任何想要的曲線。下面以三級貝塞爾曲線為例，具體介紹如何通過控制點繪制出對應的貝塞爾曲線，如圖4所示。

圖4 貝塞爾曲線

貝塞爾曲線依據四個坐標點P0、P1、P2、P3來控制生成的一條曲線，其中P0為起始點，P3為終止點，P1和P2為曲率的控制點。

根據貝塞爾曲線方程定義，以t=0.25為例，令P0P1線段的1/4處為點Q0，P1P2線段的1/4處為點Q1，P2P3線段的1/4處為點Q2，連接點Q0和點Q1，并取Q0Q1線段的1/4處為點R0，同樣的方法得到R1，連接點R0和點R1，并取R0R1線段的1/4處為點B，B點所在位置即為t=0.25時該貝塞爾曲線對應點的坐標。當t=0時對應坐標點P0，t=1時對應坐標點P3，由此t取[0,1]時，B點滑過的軌跡即為該控制點下的貝塞爾曲線。

1.4 主干網絡

本方法分別使用Resnet和EfficientNet作為主干網絡。

1.4.1 Resnet

在使用深度神經網絡去解計算機視覺相關問題時，研究者往往會堆疊多層卷決積，試圖使該網絡能夠更有效地解決復雜問題。雖然堆疊大量卷積層可以豐富模型的特征，但更深層次的網絡可能會退化，即隨著卷積層數量的增加，模型的性能可能會降低。

殘差網絡[10]（ResNet）是利用殘差塊來提高模型的性能。其核心“跳躍連接”（Shortcut Connec- tions）是這種網絡的優勢所在，如圖5右側從X到⊕的連接部分。圖5中，X表示殘差塊的輸入，F(x)為殘差塊在第二層激活函數之前的輸出，即

圖5 殘差塊

式中，w1為第一層的權重；w2為第二層的權重；σ為激活函數ReLU；σ(F(x)+x)為殘差塊最后的輸出。

跳躍連接在兩個方面起作用。第一，它們通過為梯度設置另一條捷徑，緩解了梯度消失的問題。第二，它們使模型能夠學習一個恒等函數（Identity），這確保了模型的高層不會比低層的表現差。因此，跳躍連接使得訓練更深的網絡成為可能。

1.4.2 EfficientNet

為了提高模型的性能，當得到一個基礎模型后，往往都會對模型做適當的縮放，一般的做法有：增加模型的寬度，也就是增加每一個卷積層的通道數；增大模型的深度，將每一個重復的單元增加，比如Resnet34到Resnet101的擴展；增加輸入圖片的分辨率。模型精度會隨著單一的縮放得到提升，但是它會很快就到達飽和狀態。

TAN等[11]提出了一種神經網絡架構搜索（Neural Architecture Search, NAS）的模型Effi- cientNet。該網絡提出了一種全新的模型縮放方法，將輸入圖片分辨率、寬度及網絡深度使用一種既容易計算又運算效率高的系數來進行三者之間的權衡。以EfficientNets模型為基礎，通過對其進行放大，從而得到了一系列的EfficientNets模型。由于其綜合考慮了三方面的影響，使其無論在準確率還是效率上都超越了之前所有的卷積神經網絡（Convolutional Neural Networks, CNN）模型。將它和當時準確率最高的其他模型對比，效率提高了6.1倍的同時，大小也縮小到原來的11.9%。通過遷移學習，EfficientNets在許多知名的開放數據集上都取得了優異的效果。

圖6 EfficientNet縮放示意圖

2 本文方法

2.1 模型定義

LaneBezierNet從前置攝像頭中得到輸入圖像后，為每個圖像輸出Lmax條車道線（表示為貝塞爾曲線控制點）。LaneBezierNet中包含一個用于提取車道線信息的主干網絡，在主干網絡之后添加了一個全連接層，共有N個輸出，其中N表示式（3）。

式中，n為貝塞爾曲線階數的參數；P為預測的貝塞爾曲線控制點；St為該條車道線的起始點縱坐標；Hi為該車道線終止點縱坐標，Co為預測的置信度。

LaneBezierNet采用貝塞爾曲線方程表示法而不是一組標記點。而對應的曲線則可通過該網絡輸出的P表示為

顯然，每條車道線的起點坐標的t值為0，終點坐標的t值為1。

LaneBezierNet的輸出可以表示為

式中，I為輸入圖像；θ為超參數，置信度Co≥閾值的車道線被視為有效車道線。

2.2 模型訓練

對于單個攝像頭的輸入圖像，假設L為該圖像中的帶標注的車道線的數量。通常交通場景中車道線的數量滿足L≤4。我們將每個帶標注的車道標記為j，j=1,...,L。在損失函數中，輸出L+ 1,...,Lmax有關的預測將被忽略。對于每個車道標記j，置信度定義為

對于單個圖像，使用多任務損失函數進行訓練。

式中，Lreg為均方誤差（Mean Squared Error, MSE），Lcls為二進制交叉熵（Binary Cross Entropy Loss, BCE）。

3 實驗與分析

3.1 實驗參數與設置

實驗采用 Windows 系統進行訓練及測試，編程語言為Python 3.9，深度學習框架為torch 1.11，服務器圖形處理器（Graphics Processing Unit, GPU）為NVIDIA GeForce RTX 3070 Ti 8GB。該方法選擇 Adam 優化器對參數進行優化，學習率初始值為3.0e-4，并使用余弦退火變化策略。

3.2 數據集

為了使本文中提出的LaneBezierNet模型得到充分驗證，該實驗選取了公開數據集TuSimple進行訓練。TuSimple數據集采集了高速公路上的圖片，其圖片都是在晴好天氣下的高質量圖片。數據集中包含的測試集、驗證集和測試集的具體信息如表1所示。

表1 數據集介紹

3.3 算法評價標準

用來衡量所提出方法的性能的度量標準分別是準確率（Accuracy, Acc）、假正例（False Positives, FP）率和假反例（False Negatives, FN）率。對于被認為是真正例（即正確）的預測車道標志，其精度定義為

3.4 結果與分析

3.4.1 TuSimple數據集對比

在TuSimple數據集上的實驗結果如表2所示，其為本文模型和其他模型的對比，可以看出本文模型在保持了較高的準確率同時，每秒傳輸幀數（Frames Per Second, FPS）達到116的最高水平。

表2 TuSimple數據集上的比較

3.4.2 消融實驗

從表3可以看出當使用3階貝塞爾曲線方程時，檢測效果最佳。實驗表明2階時的曲線檢測效果不好，而使用4階及以上時，曲線的自由度太大反而不好控制，從而導致生成的曲線效果更差。

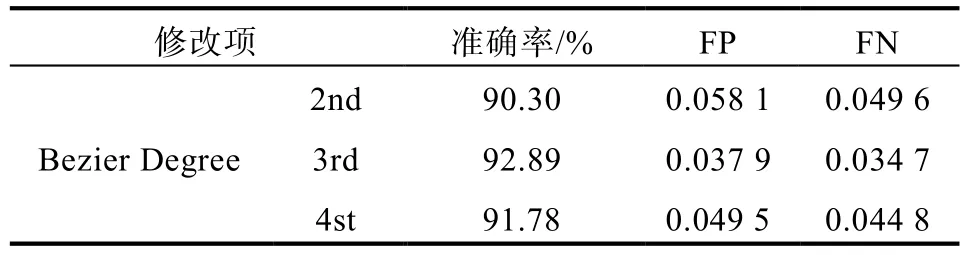
表3 TuSimple數據集上貝塞爾曲線不同階的比較

如表4所示，EfficientNet-b1達到最高精度，其次是EfficientNet-b0和ResNet-34。這些結果表明，像ResNet-50這樣的大型網絡可能會過度收集數據。盡管EfficientNet-b1達到了最高的準確度，但它的計算成本更高（更低的幀速率、更高的最大似然比和更長的訓練時間）。

4 結論

本文提出了一種基于貝塞爾曲線回歸的車道線檢測新方法。與最先進的方法相比，所提出的方法簡單有效，在保持有競爭力的準確性的同時，檢測效率得到了極大的提升。目前，本文模型檢測準確率和泛化能力上還有提升空間，在未來工作中，我們也將從這兩個方面提出更有效、靈活的建模方法，進一步提升模型性能。