2022年高考湖南卷力學計算題探析
■湖北省監利市實驗高級中學 黃尚鵬
2022年高考湖南卷第14題以拍籃球為情景,綜合考查動能定理、變力做功、動量定理等主干知識,是一道典型的動量與能量結合的力學綜合題。這道題(1)(2)問的難度不大,直接利用物理規律列式求解即可,(3)問需要利用遞推法推導出數列的通項公式,運用數學知識求解物理問題。下面深入探究這道力學計算題的求解方法,供同學們參考。
一、對高考原題的分析與解答
題目:如圖1甲所示,質量為m的籃球從離地H高度處由靜止下落,與地面發生一次非彈性碰撞后反彈至離地h的最高處。設籃球在運動過程中所受空氣阻力的大小是籃球所受重力的λ倍(λ為常數,且0<λ<且籃球每次與地面碰撞的碰后速率與碰前速率之比相同,重力加速度大小為g。
(1)求籃球與地面碰撞的碰后速率與碰前速率之比。
(2)若籃球反彈至離地h的最高處時,運動員對籃球施加一個向下的壓力F,使得籃球與地面碰撞一次后恰好反彈至離地h的高度處,力F隨高度y的變化如圖1乙所示,其中h0已知,求F0的大小。
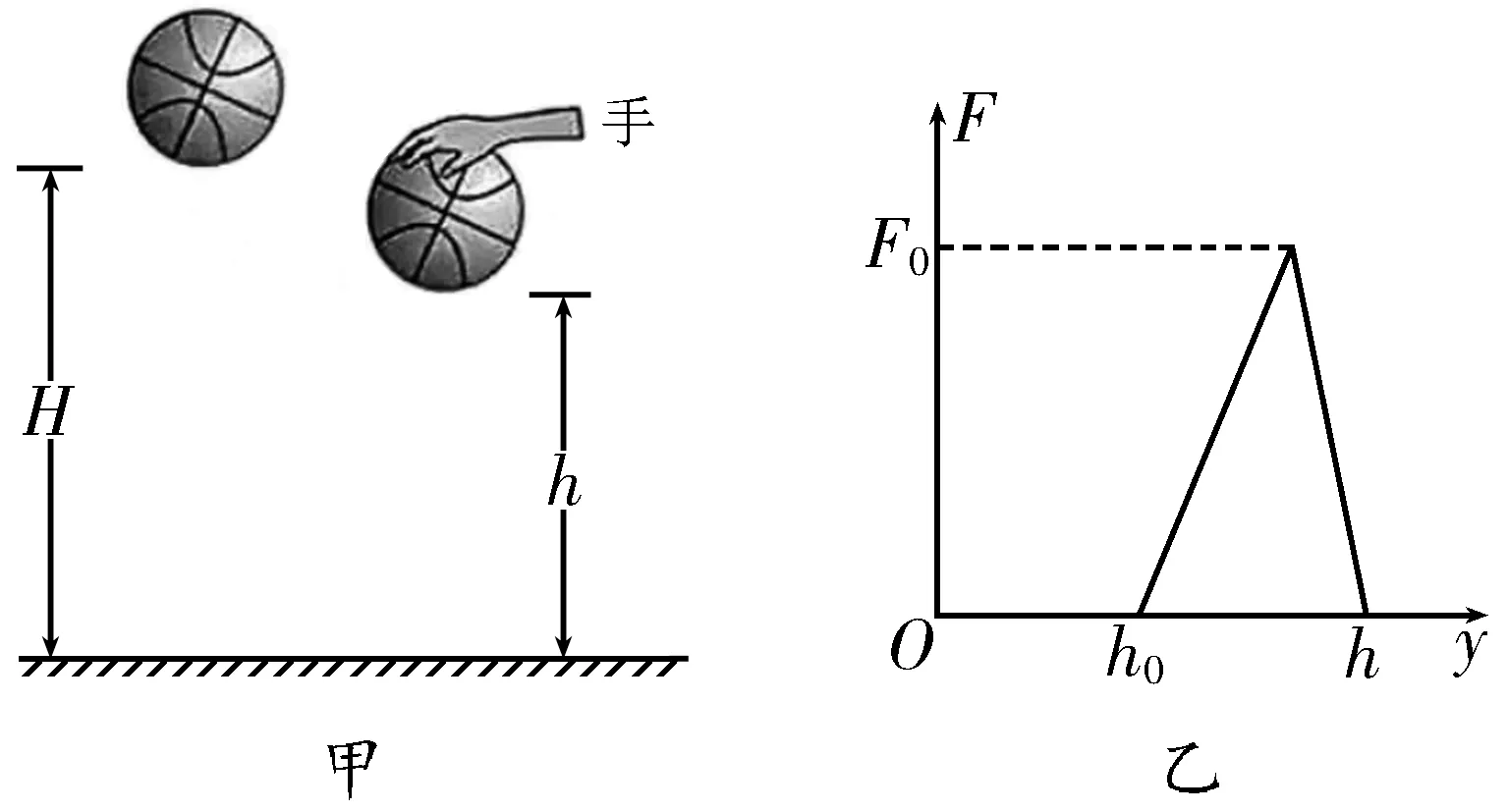
圖1
(3)籃球從離地H高度處由靜止下落后,每次反彈至最高點時,運動員拍擊一次籃球(拍擊時間極短),瞬間給其一個豎直向下、大小相等的沖量I,經過N次拍擊后籃球恰好反彈至離地H高度處,求沖量I的大小。
解析:(1)籃球從離地H高度處由靜止下落至地面的過程中,設籃球與地面碰撞的碰前速率為v前,根據動能定理得(mg-,解得籃球從與地面發生一次非彈性碰撞后到反彈至離地h的最高處的過程中,設籃球與地面碰撞的碰后速率為v后,根據動能定理得解得v后=因此籃球與地面碰撞的碰后速率與碰前速率之比
說明:由題意知籃球與地面發生的碰撞為非彈性碰撞,則解得,這與題目中給出的常數λ的范圍一致。
(2)籃球反彈至離地h的最高處時,運動員對籃球施加一個向下的壓力F,力F隨高度y的變化圖像與橫軸圍成的圖形的面積表示變力F所做的功。籃球從離地h高度處下落至地面的過程中,設籃球與地面碰撞的碰前速率為v1,根據動能定理得(mg-λmg)h+籃球再次反彈至離地h高度處的過程中,設籃球與地面碰撞的碰后速率為v2,根據動能定理得- (mg+因為籃球每次與地面碰撞的碰后速率與碰前速率之比相同,即所以(mg-λmg)h+,解得F0=
(3)籃球從離地H高度處由靜止下落后,每次反彈至最高點時,運動員拍擊一次籃球,瞬間給其一個豎直向下、大小相等的沖量I,由于拍擊時間極短,重力的沖量可以忽略不計,設擊球瞬間籃球獲得的速度為v0,選豎直向下為正方向,根據動量定理得I=mv0,即每次擊球瞬間籃球獲得的速度為定值。如圖2所示,設籃球從離地H高度處由靜止下落后,第一次反彈至最高點運動員拍擊籃球后,下落過程中的下落高度記為h0=h,著地速率為v1,反彈速率為v1',反彈后上升的最大高度為h1;第二次反彈至最高點運動員拍擊籃球后,下落過程中的下落高度為h1,著地速率為v2,反彈速率為v2',反彈后上升的最大高度為h2;…;第n次反彈至最高點運動員拍擊籃球后,下落過程中的下落高度為hn-1,著地速率為vn,反彈速率為vn',反彈后上升的最大高度為hn。
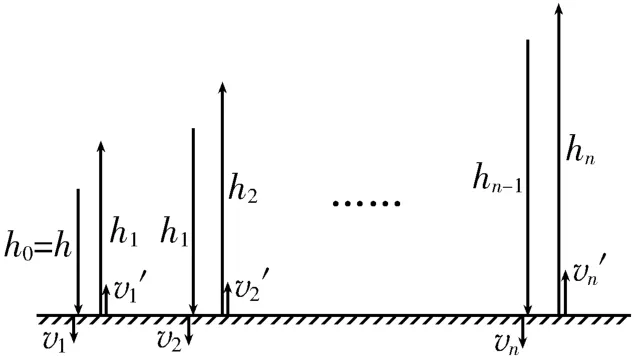
圖2
第n次反彈至最高點運動員拍擊籃球后,在籃球下落的過程中,根據動能定理得在籃球反彈后上升的過程中,根據動能定理得-(mg+籃球與地面碰撞的碰后速率與碰前速率之比解得hn=代入得令,則hn=phn-1+q(n≥1,h0=h),即數列{hn}為一階線性遞推數列。求數列{hn}的通項公式可以采用以下兩種方法。
方法一:構造等比數列法。引入待定常數α,使hn-α=p(hn-1-α),則hn=phn-1+(1-p)α,對比遞推公式hn=phn-1+q,再令(1 -p)α=q,解得故數列{hn-α}是以h0-α=h-α為首項,p為公比的等比數列。因此hn-α=pn(h0-α)=pn(h-α),即hn=pn(h-α)+α。
方法二:累加相消法。將遞推公式hn=phn-1+q(n≥1,h0=h)兩邊同時除以pn得,則,將以上n式相加得,根據等比數列求和公式得,則令即,將上式兩邊同時乘以pn得hn=pn(h-α)+α。
已知經過N次拍擊后籃球恰好反彈至離地H高度處,即hn=H,代入數列{hn}的通項公式得(h-α)+α,解得α=又有因此
說明:(3)問要求經過N次拍擊后籃球恰好反彈至離地H高度處,即要求運動員每次拍擊籃球后反彈上升的最大高度越來越大,此過程具體是如何實現的呢? 根據數列{hn}的通項公式hn=pn(h-α)+α,其中p=<1 可知,pn是遞減的,要使hn遞增,則需pn的系數h-α<0,即要求h<,解得另外,令n→∞,則pn→0,hn→α=,即當時,運動員每次拍擊籃球后籃球反彈上升的最大高度hn遞增,但hn有極限,不會無限增大。
二、對高考原題的評析
本題(1)問考查動能定理的應用(也可以運用運動學公式和牛頓第二定律聯立求解),(2)問在考查動能定理的基礎上進一步考查計算變力做功的一種常用方法——面積法,即力F隨高度y的變化圖像與橫軸圍成的圖形的面積表示變力F所做的功,(1)(2)兩問都很基礎,不偏不怪。(3)問的難度較大,考查了一種重要的數學方法——遞推法,考查利用數學知識解決物理問題的能力。所謂遞推法,即當問題中涉及的物理過程較多,且各物理過程具有相同的特點和遵循相同的規律時,可選取有代表性的任一物理過程分析,得出聯系相鄰物理過程的相關物理量的遞推關系式,再根據遞推關系式求解相關物理量的通項公式,從而達到解決問題目的的一種科學思維方法。構造等比數列法和累加相消法是求遞推數列通項公式的常用方法,由數列的遞推公式求通項公式需要抓住遞推數列的遞推關系,分析結構特征,進行合理變形。
三、探究籃球自由彈跳過程中運動的總路程
變式探究1:將本題(3)問改為籃球從離地H高度處由靜止下落后,每次反彈至最高點時,讓籃球在空中自由彈跳直到最終靜止于地面上,求籃球自由彈跳過程中運動的總路程。
解析:根據上述得出的遞推公式hn=可知,若籃球每次反彈至最高點時,運動員并不拍擊籃球,即令v0=0,則hn=(n≥1,h0=h),顯然數列{hn}是以h0=h為首項,p=<1為公比的等比數列。因此hn=pnh0=故籃球在空中自由彈跳過程中運動的總路程s=H+2(h0+h1+h2+…+hn-1+…),根據等比數列求和公式得
變式探究2:將本題改為質量為m的籃球從離地H高度處由靜止下落,與地面發生一次彈性碰撞后反彈至離地h的最高處。設籃球在運動過程中所受空氣阻力的大小恒定,且籃球每次與地面的碰撞為彈性碰撞,求籃球在空中自由彈跳過程中運動的總路程。
解析:籃球從離地H高度處由靜止下落,與地面發生一次彈性碰撞后反彈至離地h的最高處,設籃球在運動過程中所受空氣阻力大小為f,對此全過程應用動能定理得mg(H-h)-f(H+h)=0,解得f=設籃球在空中自由彈跳過程中運動的總路程為s,對自由彈跳的全過程應用動能定理得mgH-fs=0,解得
說明:變式探究2 與變式探究1 得出的結果完全相同。事實上用遞推法同樣可以證明變式探究2情形下籃球每次反彈后上升的最大高度仍然是以h0=h為首項,p=為公比的等比數列,因此籃球在這兩種自由彈跳過程中運動的總路程相同。
證明:籃球第n次反彈至最高點后,在籃球下落的過程中,根據動能定理得(mgf)hn-1=在籃球反彈后上升的過程中,根據動能定理得-(mg+f)hn=0-若籃球每次與地面的碰撞為彈性碰撞,則vn'=vn,聯立以上各式解得hn=,將代入得hn=

