面向武器站模塊化基座的多工況與靜動態筋壁結構高效設計方法
萬子平, 譚若愚, 鄭杰基, 任廣安, 謝馨, 范大鵬
(國防科技大學 智能科學學院, 湖南 長沙 410073)
0 引言
武器站是一種基于兩軸轉臺(方位軸和俯仰軸)的精密指向系統,該系統可在控制閉環下使武器的火線軸穩定地跟隨目標。隨著戰場需求的不斷變化,武器站在效能單元(武器、傳感器等)的配置上更加注重可重構設計,以便于根據需求快速配置,縮短產品設計定型時間。2017年,美國MOOG公司推出了Reconfigurable Integrated-weapons Platform可重構集成武器平臺,簡稱RIwP。該平臺對機械、傳動和驅控組件均進行了通用化設計,將產品設計定型流程(數月至數年)轉變為效能單元的換裝流程(小于1 h),縮減了產品定型時間,增強了武器站的戰場適應性。
可重構設計的優勢主要體現在通用性、重組性、擴展性、低成本、容錯性和自修復性,但存在結構冗余的問題,導致其機械特性在可重構設計中非最優,從而影響武器站快、準、穩的伺服性能。
機械特性的優化方向主要包括結構、材料和工藝。工程應用中,材料優化方法主要為選型設計,工藝優化方法主要為校核驗證,這兩個優化方向在機械特性優化中的作用相對有限,而結構優化則可以實現機械特性優化的最大延展。
結構優化設計主要包括基于局部結構參數化的尺寸優化[1]、基于全局外形參數化的形狀優化[2]和基于保留承力路徑的拓撲優化[3-4]。上述優化方法的焦點多為對優化行為的描述,而較少關注機械結構與應用背景的關系。針對此問題,又衍生出了多材料結構的多學科優化方法[5]、復雜工況下的多工況優化方法[6]、連續結構的筋壁結構優化方法[7]和離散結構的骨架化優化方法[8]。由于武器站機械結構特征為承力腔體結構,需要其具有承壓和密封特性,最適宜設計為筋壁結構形式。筋壁結構為高剛質比結構,兼顧了輕量化、高剛性、固有頻率高和穩定性高等優勢。
近期筋壁結構的優化研究包括:1)多層級并發加筋方法[9],該方法采用拓撲優化方法獲得承力筋條,采用基結構法進行局部結構加強,此類方法較適用于受力均勻的航天器結構,不太適合工藝相對復雜的武器站結構;2)生長式的筋結構成型方法[10],此類方法基于工藝方法實現筋的柔性陣列生長,多用于沖壓或軋制工藝下的板料加筋方法,不太適合武器站類鑄造結構;3)復合材料協同加筋方法[11],此類方法基于復合材料特性進行多目標下的筋壁結構設計,因為該方法中加入了阻尼板,豐富了其動態特性,但對于鑄鋁材料的武器站不太適合。綜上所述可見,依據武器站的應用背景、載荷工況和指標要求合理地設定設計目標,設計方法和優化策略尤為重要。
基于上述問題,本文基于綜合目標優化函數提出了一種多工況與靜動態的筋壁結構高效設計方法。該方法包括兩個方面:1)基于超單元的多工況與靜動態拓撲優化方法,解決拓撲優化計算消耗大的問題;2)基于靈敏度的筋壁結構響應面尋優方法,解決拓撲構型外形包絡高效成型的問題。
1 模塊化基座的綜合目標優化函數
1.1 模塊化基座的多工況優化函數
1.1.1 模塊化基座可重構特性
模塊化基座源于武器站U形架的碎片化,其之所以可以單獨成為模塊化部件,是因為可通過模塊化關聯度計算[12]模塊化基座與方位傳動軸系和俯仰傳動軸系的關聯度相等。
美國MOOG公司推出的RIwP可重構集成武器平臺如圖1所示。由圖1可知,耳軸支架和耳軸調節支架需要有一定的調節特性,而國內未系列化的多變武器負載提高了耳軸支架和耳軸調節支架的設計難度;反之,模塊化基座不存在上述問題,能完成一對多的可重構設計。

圖1 RIwP可重構集成武器平臺Fig.1 RIwP Reconfigurable Integrated-weapons Platform
1.1.2 基于功能區和射角的工況分類
構型的通用性越強,面臨的工況越多。根據武器站的外部輸入擾動可知,武器后坐力載荷是造成不同工況的主要來源,因此可通過武器布局和高低射角對工況進行分類。假設武器站典型功能區有ng個,武器站典型射角有ns個,則共可以分為ng×ns種工況,武器站工況分類如圖2所示。
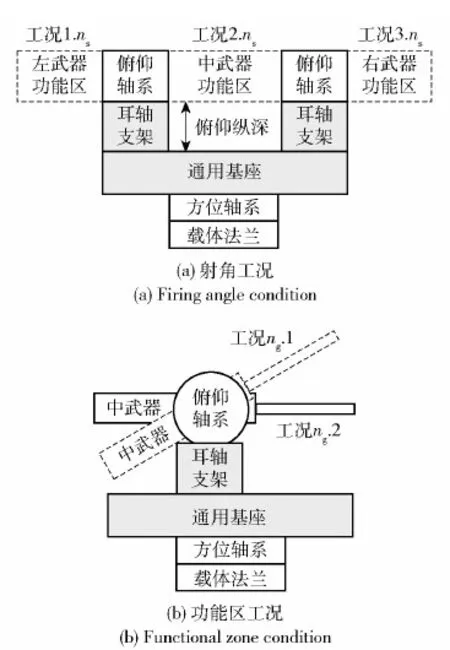
圖2 武器站工況定義示意圖Fig.2 Schematic diagram of condition definition of weapon station
1.1.3 多工況優化函數建立
在未設定具體優化目標的基礎上,與后坐力載荷相關的單工況目標函數為
Ωn=Ω(Fn),n∈{1,2,…,ng×ns}
(1)
式中:Ωn為第n種工況的目標函數;Fn為第n種情況下的后坐力。則設定多工況下的目標函數為
(2)
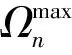
1.2 模塊化基座的靜動態優化函數
1.2.1 基于剛度的靜態特性描述
模塊化基座的剛度為主要的靜態特性優化指標,因為武器站所受大載荷除后坐力載荷外,還有負載的重力載荷和慣性載荷,過大的載荷和過低的剛度導致的結構變形會影響武器站的指向精度,從而導致觀瞄儀光軸和武器火線軸的錯位。
在連續體結構中,結構柔度等于結構剛度的倒數,結構剛度和柔度為
(3)
式中:F為載荷;K為剛度矩陣;u為位移矩陣;C為柔度矩陣。
1.2.2 基于模態的動態特性描述
在模塊化基座的模態為主要的動態特性優化指標,因為武器站的載體行進過程中會產生較低頻的道路譜激勵,過低的固有頻率和過高的道路譜激勵頻率會激發結構的諧振特性,進而影響武器站的伺服精度,導致武器站在進行目標跟隨時火線軸的隨機波動。
文獻[14]中定義了組合輪式車的加速度譜密度函數。基于加速度譜激勵輸入的動力學方程為
(4)
式中:M為質量承力構型的質量矩陣;a(t)為加速度矩陣;p(ω)為加速度激勵譜,ω輸入激勵的頻率分量;B為承力構型的阻尼矩陣;v(t)為速度矩陣;p(t)為位移矩陣,其中M、B和K與結構模態直接相關。將式(4)表述為輸入輸出方程為
(5)
式中:r(ω)為頻率響應譜。
1.2.3 靜動態優化函數建立
剛度目標函數為結構的應變能最小,應變能為
(6)
式中:ε和σ分別為載荷F下的應變和應力。
模態的目標函數為最小化結構的位移響應幅值,利用復模態疊加法[15],其第i階自由度的位移響應為
(7)
式中:mi、ki和bi分別為第i階模態的振子質量,剛度和阻尼;il為需優化的最高低階模態,由于模態階數越低,幅值響應越大,主要優化低階模態。
將式(6)和式(7)中的目標函數做等效處理,將柔度函數等效為應變能目標函數,將幅值響應函數等效為固有頻率目標函數為
(8)
式中:fs為固有頻率。
在靜態和動態目標的綜合優化中,可利用歸一化線性加權和法,將多目標問題轉化為單目標問題進行優化,結合靜、動態特性目標優化函數為
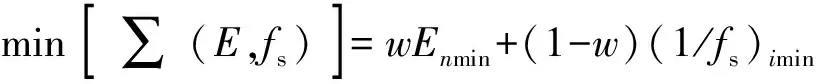
(9)
式中:w為應變能目標函數權值;Enmin為第n種工況下的應變能最小化目標函數。
1.3 武器站模塊化基座綜合目標優化函數
結合式(2)和式(9),可得在多工況和靜動態下的武器站模塊化基座綜合目標函數分別為
(10)
式中:wmi(i∈{1,2,…,il})為不同模態下的目標函數權重,由于模態是模塊化基座的固有特性,可直接通過線性加權法對wmi進行定義;(fs)i為第i階固有頻率;(fs)imax為第i階固有頻率的最大化目標函數;(fs)imin為第i階固有頻率的最小化目標函數;Enmax為第n個工況下的應變能最大化目標函數。
2 模塊化基座的高效拓撲優化策略
2.1 粗拓撲和細拓撲優化方法
2.1.1 粗拓撲方法和超單元的子結構劃分
粗拓撲可提取復雜結構中的承力構型,以避免細拓撲的計算消耗。采用水平集方法[3]進行粗拓撲較為合適,因為水平集方法尋優時采用具有分段特性的Heaviside函數,可使得拓撲邊界清晰。
綜合優化目標函數中包含的靜態工況數和模態階數多,導致優化計算量大。為提高效率,可對承力構型進行超單元劃分,劃分后的超單元應具有提供z軸方向支撐力的承壓壁、提高x軸方向模態的抗彎壁和提供y軸彎矩和z軸扭矩的防扭壁,如圖3所示。

圖3 承力構型超單元劃分圖Fig.3 Superelement division of load-bearing configuration
2.1.2 細拓撲方法和子結構優化方法選擇
細拓撲可提取承力構型的筋條路徑,為筋壁結構的成型提供基礎。細拓撲采用變密度法[4]較為合適,因為變密度法的設計變量僅為網格單元密度,可通過解析式實現多樣的工藝約束。為確保滿足鑄鋁(ZL101A)的鑄造工藝,本文引入最小和最大成員尺寸約束和分型面筋結構的拔模約束。
最小和最大成員尺寸約束可以防止出現細小筋結構和材料集中現象,其約束形式為
(11)
式中:L為離散空孔尺寸;Lmax為最大成員尺寸;Lmin為最小成員尺寸;nd為邊界離散單元個數;Sid為第id個單元的表面積;ρid為第id個單元偽密度;
分型面筋結構的拔模約束可以有效使具有筋壁結構的鑄件脫模,其約束形式為
s.t.(ρx)1≤(ρx)2≤…≤(ρx)it,it∈{1,2,…,nt}
(12)
式中:(ρx)it為拔模方向上的第it個偽密度;nt為拔模方向上的虛偽密度單元總數。
子結構優化方法可通過子結構的失效形式進行定義,子結構失效形式如表1所示。

表1 子結構的失效形式Table 1 Failure form of substructures
由子結構失效形式可知圖3結構的優化思路為:
1)軸壓壁:通過調整筋條的zy面數量和間距,以及壁結構厚度避免屈曲失穩和剪切失效,同時達到承力腔密封要求,因此需做筋壁結構設計。
2)抗彎壁:通過設計抗彎壁的zx面筋條布局和zy面截面形狀來減少剪切應力,而壁結構的連續性會導致剪切失效,因此只做筋結構設計。
3)防扭壁:通過設計防扭壁zx面和zy面的截面形狀,減少固定約束(固支邊)的彎矩和平行于xy面的封閉剪切應力流,因此只做壁結構設計。
基于失效形式的子結構優化方法如表2所示。

表2 子結構優化方法Table 2 Substructure optimization method
參考單塊式機翼的蒙皮骨架式結構[16]對細拓撲后的承力構型的筋壁結構進行表述,如圖4所示。
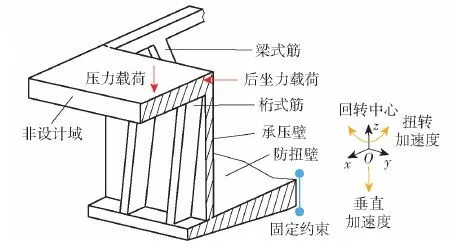
圖4 承力構型筋壁結構圖Fig.4 Load-bearing reinforced wall structure
2.2 基于超單元的細拓撲優化方法
2.2.1 子結構剛度矩陣求解方法
由于子結構會保留剛度矩陣,可完成靜態拓撲優化。由模態綜合法[17]可知,超單元分解后子結構的內部自由度為ue,邊界保留自由度為ur,則結合式(3),剛度靜態方程為
(13)
式中:Krr為子結構剛度矩陣;Kee為邊界縮聚結構質量剛度;Ker和Kre為耦合剛度矩陣;Fr為外部施加載荷;Fe為非優化子結構內部載荷。
通過式(13)的內部運算消除非優化子結構的內部自由度ue,即可得優化子結構的剛度方程為
(14)
式中:K′為超單元剛度矩陣;F′為超單元外部載荷矩陣。由于消除了ue,在拓撲優化迭代中不再計算非優化子結構的剛度方程,從而減小了計算量。
2.2.2 子結構模態矩陣求解方法
由于子結構不會保留遠端的質量矩陣,無法實現動態(模態)的拓撲優化。由模態綜合法[17]可知,忽略系統阻尼矩陣和外部載荷,其動態方程為
(15)
式中:Mrr為子結構質量矩陣;Mee為邊界縮聚結構質量矩陣;Mer和Mre為耦合質量矩陣。
由于非優化域子的結構質量較小,對其質量矩陣的縮聚對總體模態矩陣影響較小。對非優化域子的結構內部自由度進行約束(ue=0),并縮聚為遠程質量點,通過剛性多點約束(MPC)連接于邊界自由度,縮聚后的子結構的模態方程為
(16)
2.2.3 動態方程子結構劃分準則
由于在總體結構模態求解時只對總體結構的低階模態進行求解,在保留的子結構中應保留總體結構的低階模態。正則化處理的總結構和子結構的質量矩陣和剛度矩陣為
(17)
式中:I為單位矩陣;ΛL、ΛH、ΛrrL和ΛrrH為
(18)
φ和φrr分別為總結構和子結構的正則化模態,其由低階模態φL和高階模態φH組成,即
(φ,φrr)={[φL,φH],[(φrr)L,(φrr)H]}
(19)
提取總結構和子結構的低階模態,并比較低階模態(一般取前6階)的固有頻率,第i個總結構的低階頻率(f)i和第i個子結構的低階頻率(frr)i分別為
(20)
當式(20)中的子結構和總結構的固有模態頻率相近時,說明超單元的子結構劃分合理,反之需對其進行重新劃分。
2.2.4 超單元的多工況和靜動態拓撲優化方法
該方法可在ANSYS軟件中通過各功能塊結合APDL命令流編程實現,實現流程如下:
1)在軟件中通過模型編輯模塊中的Slice命令分解建立或導入的模塊化基座模型文件。
2)將遠端結構縮聚為遠程質量點,并引入n個工況的載荷和約束,靜力學求解后獲得全模型文件。
3)縮聚全模型非優化子結構形成的子模型,并將相應工況的邊界命令流引入相應子模型中。
4)進行靜力學分析,求解后評估獲得的子模型文件,并驗證子模型和全模型求解結果的一致性。
5)在共享子模型的前提下進行模態分析,在縮聚子結構的邊界上引入含有質量縮聚矩陣MPC單元。
6)求解子模型i階模態,并對比全模型i階模態,判斷引入誤差量級是否在可接受范圍內。
7)將n個工況和i階模態的子模型命令流匯聚后進行子結構的優化,并獲得優化構型。
基于上述流程,該算法實現框圖如圖5所示。

圖5 超單元的多工況和靜動態拓撲優化方法Fig.5 Multi-condition and static and dynamic topology optimization method of superelements
3 模塊化基座筋壁結構高效成型策略
3.1 基于拓撲構型的壁結構設計方法
3.1.1 基于拓撲構型的壁結構設計流程
不同工程領域的載荷水平不同,對應的筋壁結構形式也不同[7],具體分為表3中的3種情況。

表3 基于載荷水平的筋壁形式Table 3 Form of reinforced wall based on load level
武器站的載荷形式與白車身慣性載荷不同,其約束不能設定為慣性釋放[15],而應設定為固定約束,因此不能設計成薄壁高筋結構。武器站載荷形式與重型施工機械受到大碰撞載荷不同,其載荷量級和應力集中遠達不到連續壁厚結構,故承壓壁結構應為中筋中壁結構,此時壁結構起到承力作用。
基于拓撲優化的筋壁結構設計方法通常基于帶壁厚[11]和無壁厚的拓撲優化方法[7],無壁厚的拓撲優化方法計算量較小,但拓撲精度較低。帶壁厚的拓撲優化精度較高,但存在工藝約束沖突的問題。由優化目標可知,屈曲失穩和剪切破壞并不是優化目標,且拓撲精度不是主要方向。因此,本文基于無壁厚的拓撲優化方法設計筋壁結構,其流程圖如圖6所示。

圖6 基于拓撲優化的壁結構設計流程Fig.6 Design flow of wall structure based on topology optimization
3.1.2 基于失效約束的壁結構設計方法
由圖4可知,壁結構的失效源于壓力載荷造成的屈曲失穩和后坐力載荷造成的剪切破壞[15],對于各向同性的金屬材料壁結構,局部屈曲許用應力[7-15]為
(21)
式中:[σ]N為材料屈曲許用應力;kN為屈曲失穩系數;EN為材料彈性模量;Lt為壁厚度;Ls為筋條間距;kr為筋條支持系數。
局部剪切許用應力[15]為
(22)
式中:[σ]s為材料剪切許用應力;ks為局部破壞系數;Es為材料剪切模量;Ll為筋條長度。
根據分析可知,許用應力在計算時,筋條方向需與載荷方向正交,由于拓撲優化的筋條路徑為非規則排布,難以利用式(21)和式(22)直接進行計算。
針對以上問題,本文提出一種基于載荷和筋條路徑的壁厚計算方法。在載荷方面,利用von Mises應力(等效應力),將外載荷正交分解為壓力載荷和剪切載荷,并作為壁厚設計依據。在筋條路徑方面,利用離散化方法將筋條分解為剪力向和壓力向的筋條微元,將等水平線位置的壓力向微元間的壁結構的屈曲和剪切許用應力分別等效為式(21)和式(22)。
首先根據壓力載荷方向對筋條路徑離散化;然后截取壓力向微元間的最大間距;最后計算屈曲應力和剪切應力下的最小壁厚,并選取較厚壁厚為壁結構厚度。筋條離散化和間距截取方法如圖7所示。

圖7 筋條離散化和間距截取方法Fig.7 Reinforcement discretization and spacing interception
基于載荷和筋條路徑的壁結構厚度計算公式為
(23)
式中:(Lt)N、(Lt)S分別為根據屈曲許用應力和剪切許用應力求解的壁結構厚度。
3.2 基于靈敏度的響應面尋優策略
3.2.1 基于試驗設計的響應面模型
由于拓撲優化的筋條包絡不規則,為簡化工藝可采用矩形筋條逼近筋條外形。而矩形筋條的參數尋優可采用響應面法[5],其包括試驗和模型設計。
在試驗設計方面,本文采用拉丁超立方體抽樣設計方法。在采樣點數選擇時,采用中心復合設計方法得到
No=1+2no+2no-o
(24)
式中:No為樣本點數目,o為筋條和壁的總水平數目(筋高、筋厚和壁厚);no為筋條和壁的總數目。
在模型設計方面,本文采用可彌補多項式響應面不適應輸入變量產生非線性振蕩的Kriging模型,結合筋壁結構參數的Kriging模型為
G|r(lm)|=Gf(lm)+GZ(lm),m∈{1,2,…,o}
(25)
式中:lm為第m個筋壁結構的設計變量;Gf(lm)為第m個多次響應面模型;GZ(lm)為第m個期望為零殘差模型。
3.2.2 基于靈敏度分析法的筋壁結構尋優
響應面選定筋高、筋厚和壁厚為輸入變量,確定最低剛度和最低模態為優化目標。為簡化輸入參數變量,通過靈敏度分析法篩選與剛度和模態相關的高靈敏度變量進行參數優化,其中輸入變量的剛度靈敏度和模態靈敏度函數分別為式(26)和式(27):
(26)
(27)
式中:E為應變能;Δlm為變量變化量;Φ為模態向量。
基于高靈敏度參數變量的二次優化函數為
(28)
式中:lh為高靈敏度輸入變量;(1/fs)max最低階模態;(E)max為最高應變能工況;m′s為質量上限;ms為參數化模型質量。
本文應用基于快速非支配排序遺傳算法(NSGA-II方法)的多目標遺傳算法(MOGA)尋找參數化的最優承力構型。
4 仿真設計方法與實際工程算例
4.1 綜合目標函數權重定義
武器站受力來源為武器后坐力和重力過載[18]。重力過載和武器后坐力沖擊情況如表4所示。
射角工況本文考慮最大仰角擊發和水平擊發兩個極限射角工況。射擊功能區工況本文考慮3個射擊功能區工況。基于不同射角(2種)和不同功能區(3種)共能確定2×3種(6種)工況。
根據武器站的驗收標準,兩種射角工況,水平射角工況更為重要。3種功能區工況,中功能區工況更為重要。基于層次分析法[17]設計工況的權重,數據歸一化處理后,6種工況的權值如表5所示。

表4 重力過載沖擊和武器后坐力沖擊Table 4 Gravity overload impact and weapon recoil impact

表5 工況權重Table 5 Working condition weight
由于武器站對低階(前3階)機械模態要求較高,通過線性加權法定義其模態權重,如表6所示。

表6 模態權重Table 6 Modal weight
4.2 粗拓撲承力構型算例
模塊化基座的承力構型提取的步驟為:首先根據設計簡圖進行三維建模設計,形成初級構型;然后在初級構型上結合綜合目標函數,并利用水平集方法進行粗拓撲;最后在拓撲構型上進行二次構型,得到承力構型。承力構型的提取流程如圖8所示。

圖8 承力構型的提取流程Fig.8 Extraction process of load-bearing configuration
圖8中,水平集方法的拓撲構型存在局部孔隙化,不滿足工藝和局部剛質比低等問題,因此需要通過變密度法進行二次構型。
4.3 超單元子結構劃分與前處理算例
超單元除可進行高效拓撲優化外,同時可引入分區網格,使精確的六面體網格得到應用。子結構劃分圖和分區六面體網格圖如圖9(a)和圖9(b)所示。
承力構型約束非優化子結構的內部自由度后,邊界載荷分別如圖10(a)和圖10(b)所示。
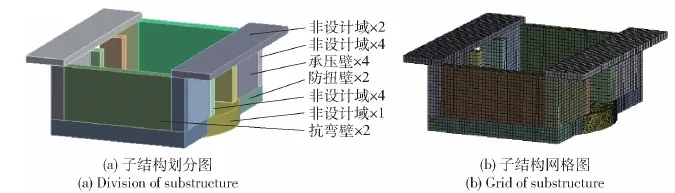
圖9 承力構型的子結構劃分圖和網格圖Fig.9 Diagrams of substructure division and grid

圖10 承力構型邊界載荷圖Fig.10 Load-bearing configuration boundary load
將非優化子結構的質量矩陣縮聚為質量點引入MPC單元后,會引入稍許的誤差。取超單元承力構型的前6階模態的固有頻率與圖8的承力構型作比較,兩種構型的模態精度對比結果如表7所示。可見,質量矩陣縮聚后,確實會引入模態誤差,但是在可接受范圍內。

表7 模態精度對比Table 7 Modal accuracy comparison
4.4 超單元的多工況與靜動態細拓撲效果論證
4.4.1 多工況與靜動態拓撲優化效果論證
為驗證超單元的多工況和靜動態拓撲優化方法的有效性,在質量約束(30%)和全局von Mises應力約束(230 MPa)下對承壓壁和抗彎壁進行拓撲優化,若成功收斂則代表質量約束可行,且為最優化輕量化構型。分別利用多工況靜態拓撲優化方法[6]、動態(模態)拓撲優化方法[16]和多工況和靜動態的拓撲優化方法對承壓壁和抗彎壁進行拓撲優化,結果分別如圖11(a)、圖11(b)和圖11(c)所示。

圖11 承力構型拓撲圖Fig.11 Load-bearing configuration topology
由圖11可見,圖11(c)的承壓壁拓撲結果與圖11(a)相似,均具有高的承壓特性;圖11(c)的抗彎壁拓撲結果與圖11(b)相似,均具有較高的擺振固有頻率;圖11(c)拓撲方法有效地彌補了圖11(a)拓撲方法低固有頻率的缺陷,同時有效地彌補了圖11(b)拓撲方法的低剛度缺陷。
取圖11中不同拓撲結果6種工況下的最大變形和前3階的固有頻率進行對比,結果如表8所示。
由表8可知,圖11(c)相對于圖11(a)構型具有更高的固有頻率,相對于圖11(b)構型具有更高的結構剛性,可見多工況和靜動態的拓撲優化有效地兼顧了剛性和模態的協同優化。

表8 優化方法對比Table 8 Comparison of optimization methods
4.4.2 超單元的拓撲優化效果論證
基于雙核分布式運算的全模型和超單元的多工況以及動靜態拓撲優化方法所用的網格數量,節點數量,計算時長和迭代步如表9所示。
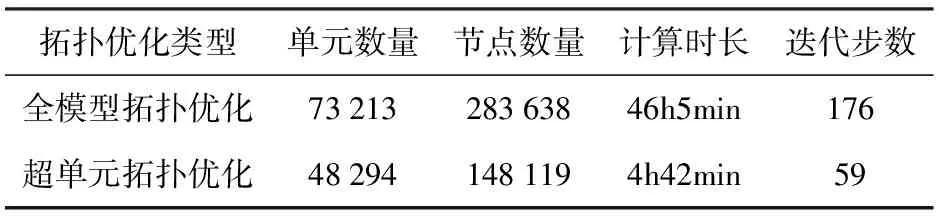
表9 計算消耗對比Table 9 Comparison of computational cost
由表9可知,超單元的拓撲優化方法在綜合優化目標下的求解時長相對于全模型的拓撲優化方法縮減了92%,充分驗證了其優越性和必要性,同時優化構型極為相似,不再贅述。
4.5 參數化筋壁結構成型算例
4.5.1 壁結構設計效果論證
壁結構設計主要與承壓壁筋條間距相關,通過圖11(c)的拓撲結果和外載荷為對稱載荷,對單側的筋條進行選取,選取結果如圖12所示。
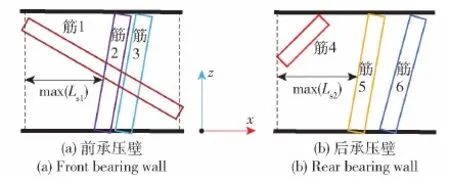
圖12 軸壓壁參數化筋條選擇圖Fig.12 Parametric reinforcement selection of bearing wall
選取max(Ls1,Ls2)=0.09 m作為最大間距,經過式(20)計算可得屈曲失穩系數kN=4,經過式(21)計算可得剪切失穩系數ks=7.2,根據式(23)可得屈曲失穩和剪切破壞約束下的最小壁厚為0.008 m和0.007 m,這里取壁結構厚度為0.008 m。
壁結構設計完成后,將圖11(c)的不規則筋條擬合成矩形筋條,可得參數化構型如圖13所示。
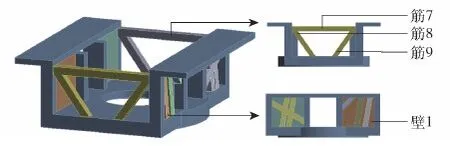
圖13 承力構型參數化三維模型Fig.13 Parametric 3D model of load-bearing configuration
為驗證壁結構是否屈曲失穩或剪切破壞,其靜力學分析后的參數化構型各工況下的壁結構最大von Mises應力如表10所示。

表10 壁結構最大應力Table 10 Maximum stress of wall structure
由表10可知,壁結構von Mises最大應力均小于材料(ZL101A)許用應力230 MPa,由此可知基于失效約束的壁厚能有效避免屈曲失穩和剪切破壞。
4.5.2 基于靈敏度的筋壁結構成型效果論證
選取圖12中6條筋的高度和厚度以及承壓壁厚度,共13個設計變量;選擇圖13中3條筋的高度和厚度,一共6個設計變量。為方便電子箱安裝和簡化設計變量,設定軸壓壁的筋高一致,抗彎壁的筋高一致,共12個設計變量。
通過式(24)計算出試驗次數為252次,在6個工況和3個模態下進行計算,此時解算次數達到(252×9)2 268次,試驗時長達到52 h32 min。為縮減計算消耗,對工況3和1階模態下的12個設計參數進行靈敏度分析,結果如圖14所示。

圖14 參數靈敏度分析結果Fig.14 Parameter sensitively analysis result
由圖14可知,將靈敏度超過3%的參數設定為高靈敏度參數(為8個),則試驗次數為147次,在2個工況和1個模態下的解算次數為(147×3)441次,試驗時長為6 h33 min,由此縮減了83.7%的試驗時間。
選擇軸壓壁筋高和抗彎壁筋高兩個靈敏度超過20%的參數,表征剛度(見圖15(a))和模態(見圖15(b))響應面,可看出筋的尺寸增加可有效減小應變能和增加1階固有頻率,其Kriging響應面如圖15所示。
此時通過建立好的響應面模型,利用多目標遺傳算法及式(28)對響應面模型進行優化,限定質量參數不再增大,優化前后的8個參數如表11所示。優化后可看出,抗彎壁的筋高縮減到了設定的下界0.02,其余都增大到了設計上界0.03。
對承力構型重新建模,對比優化前、后承力構型6個工況下的剛度、模態和質量參數,如表12所示。由表12可知:承力構型整體質量降低了28%,雖然剛度和模態雖然有所下降,但是其為最優輕量化構型;低階模態均大于速度環伺服頻率90 Hz,同時優化前后低階模態變化量較小,而高階模態下降較快,有效地兼顧了輕量化和良好的動態特性。
4.6 基于最優承力構型的校核驗證與樣機實現
在最優構型上,添加腔結構和互換性結構,以滿足電子箱的安裝密封性和功能部件的可重構性要求,最終構型及其適配的四款典型武器站如圖16所示。
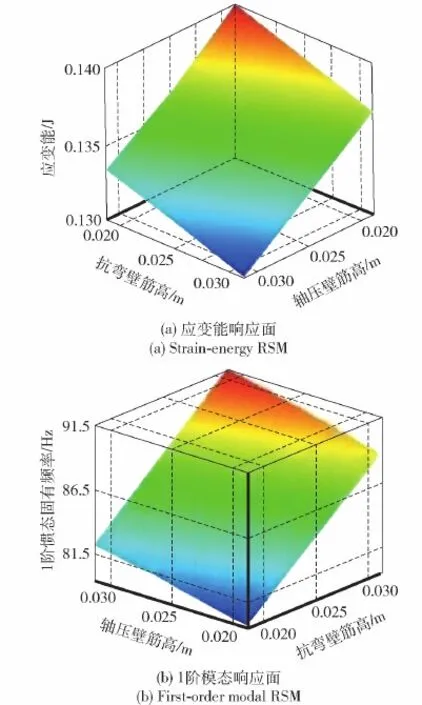
圖15 Kriging響應面Fig.15 Kriging RSM

表11 優化參數Table 11 Optimization parameters

表12 優化前后指標Table 12 Indexes before and after optimization

圖16 國產可重構集成武器平臺Fig.16 Domestic re-configurable Integrated-weapons Platform
模塊化基座的成型后的評價指標主要為基于強度的安全系數和基于剛度的振動位移。
安全系數指標在綜合目標優化函數中體現為失效約束。進行校核時,應結合時域還原其瞬態沖擊工況。結合文獻[13]的墜撞安全試驗,選用具有合理允差的后峰鋸齒脈沖作為重力過載沖擊;選用實測重載機槍后坐力時域波形[19],并將其離散為后峰鋸齒脈沖作為后坐力沖擊。極限沖擊時域激勵如表13所示。

表13 極限沖擊時域激勵Table 13 Time domain excitation of limit impact
將后坐力和慣性力加載到模塊化基座上,前25 ms的應力曲線和安全系數曲線如圖17(a)、圖17(b)所示。
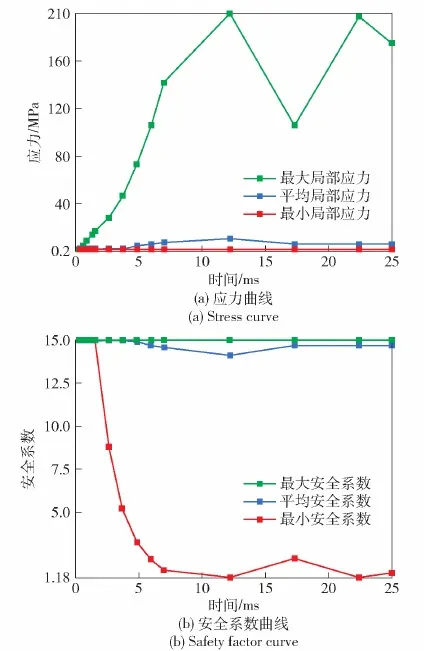
圖17 應力曲線和安全系數曲線Fig.17 Stress curve and safety factor curves
由圖17可知,在極限工況下,安全系數均處于臨界值偏上,這樣可很好地兼顧結構強度和輕量化程度,達到輕量化設計最優效果。
振動位移指標在綜合目標優化函數中與靜態剛度和模態相關,其能綜合表征系統的指向精度和伺服精度。進行校核時,將x軸、y軸、z軸方向的頻域加速度譜密度函數[13]作為激勵加載到模塊化基座上,其x軸、y軸、z軸方向的位移響應云圖分別如圖18(a)、圖18(b)和圖18(c)所示。
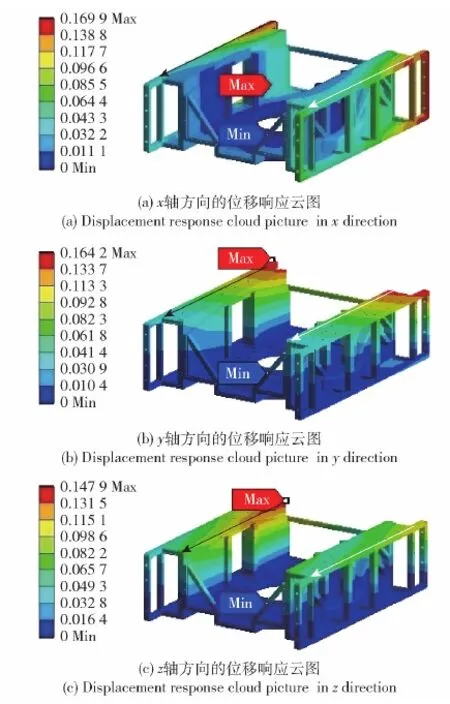
圖18 三向位移響應云圖Fig.18 Displacement response cloud pictures in three directions
圖18中,黑、白色箭頭分別代表左、右安裝面的形變最緩梯度線。參考圖8坐標系可知:當箭頭方向一致時,會造成繞y軸的彎曲形變;當箭頭方向相反時,會造成繞z軸的扭轉形變。由圖18可知,x軸、y軸、z軸方向的載荷譜均會造成繞y軸的彎曲形變,可近似定義誤差表達式為
e=max {[max (s)-min (s)]/lg}
(29)
式中:max (s)和min (s)分別表示安裝面最大、最小形變位移;lg為形變最緩梯度線長度。由式(29)可近似計算出影響指向精度和伺服精度的誤差為0.16 mrad小于射擊精度指標(CEP=1 mrad)[20],滿足設計要求。
校核完畢后,為驗證模塊化基座的可加工性及快速可重構性,對其進行試制,應用模塊化基座的某型競標武器站現場裝配結構如圖19所示。

圖19 模塊化基座現場裝配圖Fig.19 Drawing of field assembly of modular base
試制完成后的模塊化基座在標準化驗收流程中均滿足各項預期性能指標。由此即完成了國產化武器站模塊化基座的整體設計、加工、裝配和應用。
5 結論
本文設計完成了國內第一款武器站模塊化基座,在武器站領域有一定的開創性意義。得出主要結論如下:
1)模塊化基座應在多工況下以結構剛度和模態為優化目標進行輕量化設計,以保證武器的指向精度和伺服精度。
2)模塊化基座應基于超單元法進行綜合目標優化函數下的拓撲優化,以確定筋結構的布局與初始截面參數,減少綜合目標函數下的計算消耗。
3)模塊化基座可通過基于失效約束壁厚設計方法快速設計壁結構,并可基于靈敏度分析進行筋壁結構的響應面參數尋優,以簡化實驗設計計算消耗。

