基于任務演化重要度的合成部隊維修器材兩級配置優化方法

吳巍屹， 賈云獻， 史憲銘， 劉彬， 劉潔， 尹世莊， 朱曦

(陸軍工程大學石家莊校區 裝備指揮與管理系， 河北 石家莊 050003)

0 引言

合成部隊是陸軍轉型建設的重要新生作戰力量，所屬裝備型號繁多、結構復雜，同時現代戰爭的突發性、高機動性、高破壞性，致使裝備維修保障難度增加。隨著近年來實戰化演習演訓活動的增加，合成部隊在遂行區域任務時需攜行必備維修器材實施維修保障，由于任務空間的局限性，維修器材的合理配置將很大程度影響保障效果。

當前許多高新裝備集多種功能于一體，組成結構復雜、部件邏輯關聯度高。由于裝備作戰運用過程中在不同階段對系統功能需求不同，導致在不同任務階段下部件功能狀態對裝備系統功能狀態的影響也存在較大差異。在制定維修器材攜行方案時，應對不同任務階段部件狀態對裝備系統功能的影響加以考慮，合理區分部件重要度，盡可能在滿足任務空間局限性的同時充分考慮部件重要度這一影響因素，盡量避免因重要部件短缺而影響裝備系統功能的正常發揮。

一直以來，對維修器材攜行方案進行合理規劃是裝備維修保障領域的重點和難點問題。在維修器材的多級供應保障模型構建方面，1968年Sherbrooke[1]提出了經典MERTIC和VARI-MERTIC庫存控制理論模型，該理論被廣泛應用于各軍種和地方領域，取得了很多工程實踐，如航空裝備、基地艦船、民機航材的備件保障系統優化[2-4]，之后很多學者在此基礎上對MERTIC理論模型進行了優化改進。孫江生等[5]考慮了武器裝備貴重備件修理與供應的現實需求，建立了三級修理供應體制下貴重備件庫存保障模型，開展了面向多等級多層級保障系統的備件庫存保障模型研究[6-7]。蔡芝明等[8]分析了備件需求的穩態與非穩態特點，建立了備件動態配置模型。在維修器材庫存控制優化研究方面，趙建忠等[9]考慮備件質量、體積、費用任一約束建立器材配置單因素優化模型。也有部分學者綜合多個因素、多種約束條件開展器材配置優化研究[10-13]，通過引入拉格朗日算子將多約束轉化為單一約束，進行多約束條件下備件配置方法研究。

現有文獻大多未考慮不同任務階段部件重要度對備件配置的影響，文獻[14-16]僅就備件關鍵性、重要度進行了專家定性描述或行業領域分類，對于部件重要度的評價不能依據實際任務階段特點和裝備功能需求給出定量描述。另外，合成部隊尚屬新生事物[17]，器材配置相關問題研究目前正處于初步階段，僅在考慮遭敵打擊情況下建立備件需求仿真模型和單級庫存配置優化模型[18]上有相關研究，在兩級器材保障運行機制下合成部隊維修器材配置優化問題尚未見相關研究成果。

綜上所述，本文針對不同任務階段部件功能狀態對裝備系統功能狀態影響程度不同的實際，研究建立裝備部件的任務演化重要度模型，并以備件保障度為目標，構建考慮任務演化重要度的多約束條件下維修器材兩級動態配置優化模型，通過算例分析驗證模型的可行性。希望下一步可以為合成部隊指揮員制定部隊平時和戰時器材配置方案提供一定的方法支撐。

1 合成部隊兩級器材保障運行機制分析

1.1 裝備構成分析

合成部隊可獨立遂行作戰任務，其裝備構成是實施作戰任務的主體和保證，主要包括裝甲裝備、火炮裝備、防空裝備等裝備類型。裝備通常具有多層次的結構特點，按照從高到低的次序，依次劃分為裝備、子系統、部件、元器件等。由于裝備發展強調系列化、模塊化，合成部隊所屬裝備(這里以某型火箭炮為例)均可以分成底盤系統、火控系統、指控系統等多個子系統，各個子系統均是由多個部件構成，各部件之間的關系以可靠性連接關系進行描述，常見的連接關系有串聯、并聯、混連、表決系統等。綜上所述，合成部隊裝備層次結構如圖1所示。

1.2 兩級器材保障運行機制分析

圖1 合成部隊裝備結構層次Fig.1 Hierarchical diagram of equipment structure of synthetic force

裝備維修作業體系是進行維修器材配置優化的基礎。目前，隨著裝備的發展變化，裝備維修由傳統的三級維修作業體系逐步向兩級維修作業體系轉變[19]。不論是部隊級維修還是基地級維修，都可看作是在兩級維修保障系統下實施的維修保障。本文主要基于部隊級維修構建兩級維修器材保障模式，由本級和上級兩級維修器材保障系統構成，其器材存儲機構與修理機構相互對應，主要采取一個中心倉庫對應多個本級倉庫的兩級層級結構。當裝備可更換單元發生故障后在本級換件修理，若本級倉庫有所需維修器材則立即更換到裝備中，若沒有則向上級中心倉庫發出請領，上級中心倉庫沒有該種器材則應向基地級器材倉庫請領或進行外部購置；換件修理后將故障件送至具有相應維修能力的修理機構，修復后在該級別倉庫存儲，若不能維修則組織報廢。具體運行流程機制如圖2所示。

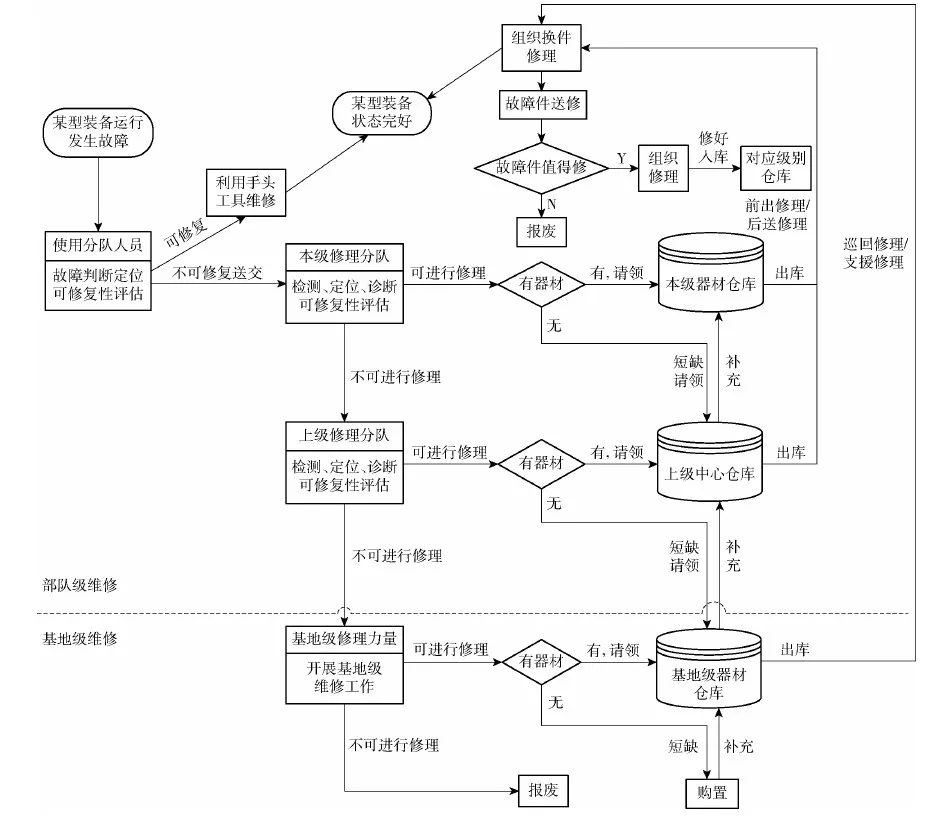
圖2 合成部隊兩級維修保障系統運行流程Fig.2 Operation flow chart of two-echelon maintenance support system of the synthetic force

顯然，在部隊級維修作業體系下兩級器材保障系統運行中維修器材的合理配置是一個關鍵性問題，對于有效實施維修保障、合理使用保障費用具有重要影響。

2 任務演化重要度模型分析

合成部隊作為獨立遂行作戰任務的作戰單位，其任務的順利達成需要不同作戰階段各作戰單元子系統之間相互配合。由于裝備系統在不同階段下任務剖面不盡相同，所要求實現的功能需求也有所不同，各個部件的重要度對于裝備系統也有差異。

部件重要度是指部件的功能狀態對裝備系統功能狀態的影響程度[20]；任務演化重要度是指綜合考慮裝備系統作戰運用過程中不同任務階段下部件功能狀態對裝備系統功能狀態的影響程度，可以用來發現系統薄弱環節，為提升裝備任務可靠性、優化器材配置提供依據。

隨著科學技術的發展，裝備結構發展經歷了從簡單到復雜、再由復雜到簡單的進化過程，特別是高新、復雜裝備在高可靠性要求之下，對裝備的結構要求越簡單越好，從過去復雜拓撲結構演變為簡單的串聯、并聯、混連結構，以提高單元間相互獨立性，并降低部件的關聯性[21]。由于不同任務階段裝備主要工作子系統完成功能的時序關系、安裝數目以及最小工作部件數均有不同，裝備部件的任務演化重要度可以通過不同任務階段下裝備系統可靠性框圖進行物理描述，如圖3所示。因此，需要結合實際任務階段情況分析部件功能狀態對裝備系統功能狀態的影響，進而探索裝備部件的任務演化重要度規律。

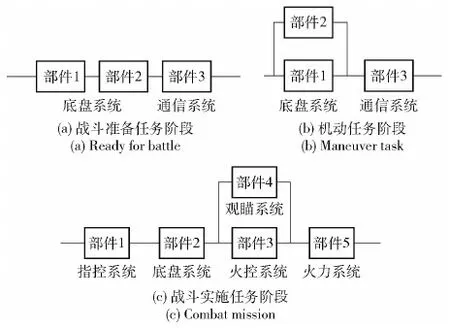
圖3 不同任務階段下裝備可靠性框圖Fig.3 Schematic diagram of equipment structure under different tasks

假設系統與部件具有故障和工作兩個狀態，其中狀態0表示故障，狀態1表示正常，且部件之間相互獨立，

系統正常狀態發生的概率為

P[X(t)=1]=R(t)E[X(t)]=0×P[X(t)=0]+1×P[X(t)=1]=P[X(t)=1]=R(t)

式中：R(t)為t時刻系統的可靠度；E[X(t)]為X(t)的數學期望。

系統正常狀態下的結構函數為

Φ(X(t)=1)=Φ(x1(t)=1,x2(t)=1,…,xn(t)=1)P(系統正常)=R(t)=E[Φ(X(t))]=P[Φ(X(t))=1]

式中：xi(t)表示裝備在不同任務階段時系統組成結構所涉及的各個部件i在t時刻的狀態。由于部件之間多以串聯、并聯、混連關系表示系統的組成結構關系，這里假設：

串聯關系為

并聯關系為

式中：n為系統組成結構所涉及的所有部件總數；Pi1(t)為t時刻部件i的可靠度；R(t)為t時刻系統的可靠度。

二態系統各部件的任務演化重要度描述了部件可靠性變化對系統可靠性變化的影響程度，用Ii(t)表示，

(1)

由于裝備在不同任務階段剖面下的組成結構不是一成不變的，單純的串聯、并聯過于簡單，本文重點以混連結構見圖3(c)進行研究，分析部件的任務演化重要度與系統組成結構的依存關系。

1)系統的結構函數為

φ(X(t))= min {X1(t),X2(t),max {X3(t),X4(t)},X5(t)}

則系統可靠度表達式為

R(t)=P11(t)·P21(t)· [1-(1-P31(t))·(1-P41(t))]·P51(t)

2)計算各部件的任務演化重要度Ii(t)

參照式(1)求導計算，以部件1為例，可以得到部件1在此任務階段下的任務演化重要度I1(t)：

I1(t)=P21(t)P51(t)(P31(t)+P41(t)-P31(t)P41(t))

式中：Pi1(t)可根據裝備在研制、定型和使用階段獲得的詳細可靠性數據得到。同理，可依次得出各部件任務演化重要度Ii(t)的排序，為下一步進行器材配置考慮部件的任務演化重要度這一重要因素奠定基礎。

3 基于備件保障度的兩級維修器材配置優化模型

通過分析合成部隊兩級器材保障運行機制，為提高整體保障效能，應當從系統角度考慮兩級維修器材的配置與優化問題，實現在有限維修保障資源條件下保證裝備的戰備完好性和任務成功率。

3.1 兩級器材保障系統構成

為便于系統建模，下面著重討論部隊級兩級維修器材保障系統裝備可修部件處理流向簡化模型如圖4所示。

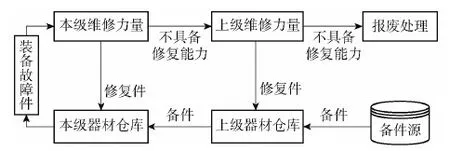
圖4 可修部件處理流向簡圖Fig.4 Flow diagram of repairable parts handling

部隊級兩級器材保障系統由兩級維修機構、兩級器材倉庫、購置備件源及備件的報廢處理等要素組成。損壞裝備作為維修保障系統的保障對象產生對器材的需求，兩級維修機構負責對故障件的修理或報廢。

3.2 備件保障度模型

為較準確地評價器材保障效果，解決好現有器材保障條件下最大保證裝備正常工作的現實問題，可采用“裝備平均工作時間、使用可用度、裝備完好率”等評價部隊訓練、戰備工作活動的指標來衡量器材配置效果，這類指標與器材的配置數量、備件延誤時間、平均維修時間緊密相關。通過分析兩級器材保障系統的運行過程，在不考慮其他影響裝備停機情況如維修時間長、等待維修人員、維修機工具等因素且故障件維修存在一定報廢率的情況下，備件供應延誤主要取決于備件周轉延誤以及庫存短缺[22]，若器材配置合理，庫存較為充足，則通過“備件周轉”可以消除這一問題。因此，僅從備件保障的角度來看，備件延誤一定程度上會影響裝備使用可用度，為較準確地刻畫這一影響，本文定義了備件保障度并給出基于備件保障度的兩級維修器材動態配置模型，旨在分析備件保障度對于裝備使用可用度的變化影響，為較好地解決維修器材配置優化問題提供參考指標。

1)定義

備件保障度As：裝備在規定條件下，可用時間與可用時間和備件延誤時間之和的比值。

(2)

式中：MUT為裝備平均可用時間；Ts為裝備平均備件供應延遲時間。

2)備件保障度與裝備使用可用度的關系

式中：A0為裝備使用可用度；MDT為裝備平均不能工作的時間；MDT′為除去備件延遲時間以外的其他總停機時間比如維修時間、等待維修人員、維修機工具等時間，

(3)

參考文獻[23]中系統可用度分析中定義裝備的固有可用度表示為

A′0在只考慮修復性維修時為裝備的固有可用度；在綜合考慮修復性和預防性維修時為裝備的可達可用度，該值與裝備先天的固有可靠性和維修性有關，后期可通過不斷系統設計與改進予以檢驗完善。為簡化計算，這里約定A′0為一常數，式(3)轉化為

可以看出A0與備件保障度As為線性相關關系，因此，裝備使用可用度A0在一定意義上可通過提高備件保障度As得到提升。

3.3 兩級可修器材庫存配置優化模型

3.3.1 模型假設

部隊在遂行實際作戰任務期間，由于本級維修能力有限，通常以換件修理為主要方式，即采用備件對故障件進行更換；若裝備因重要功能部件發生短缺，則裝備無法完成規定的任務。為方便建模，本文作如下條件假設：

①上級維修力量負責K個本級裝備維修和器材供應保障，第i個(i=1，…，K)本級維修力量負責第j種裝備共計μij臺裝備的維修和器材供應；

②器材的需求為泊松過程；

③裝備換件維修時間可忽略不計；

④不同類別可更換單元對備件的需求相互獨立；不考慮本級器材保障系統之間的橫向調劑；器材保障系統處于穩態。

3.3.2 基于備件保障度的兩級維修器材配置模型

本文在文獻[23]維修資源的確定與優化中維修器材數量確定的基礎上，構建了基于備件保障度的兩級維修器材配置模型。

1)上級器材庫存缺貨數的計算

上級器材倉庫得到備件的平均時間tl內庫存需求量Yj(j為某型裝備上第j類可更換單元(j=1,2,3,…,n))的概率密度函數為

(4)

式中：yj為第j類可更換單元在一定時間內需上級倉庫供應的備件數量；αj,o表示上級器材倉庫備件需求率，

αj,o=∑∑αij(1-rij)tl=φjtc+(1-φj)td

αij為第i個本級維修保障機構所保障的某型裝備中第j類可更換單元對備件的需求率，rij為本級修理率，即第i個本級修理機構能夠修理第j類故障件的數目占第j類故障件總數的比率，φj為第j類故障單元的報廢率，td和tc分別表示平均上級修復時間和平均上級購置時間。

因此，在tl內上級器材倉庫庫存水平為So,j時缺貨數Di(So, j)的期望值為

(5)

2)本級器材庫存得到備件時間Tj的確定

令ηj表示上級庫存缺貨率，即在tl內上級倉庫庫存的平均缺貨數與需求數的比率，有

則本級器材倉庫得到備件的平均時間Tj為

Tj=rijtb+(1-rij)[to(1-ηj)+(to+tl)ηj]=rijtb+(1-rij)[to+ηjtl]

(6)

式中：tb為平均本級修復時間；to為平均本級請領周轉時間。

3)本級器材庫存短缺數的計算

與式(5)的計算思路相同，可得到在Tj內本級器材倉庫庫存水平為Sj時，本級器材倉庫備件期望短缺數E[Bi(So,j,Sj)]為

(7)

(8)

式中：xj表示本級器材倉庫在Tj內對第j類可更換單元的備件需求量。

4)備件保障度的計算

設ξi表示本級器材倉庫庫存缺貨率，則

對于給定任務時間t內，每一個第j類可更換單元(假設每個裝備上有j類單元qj個)，由于缺少備件造成的裝備停機時間為

每一個第j類單元的備件保障度為

(9)

對于本級維修任務中，每型裝備的第j類可更換單元的備件保障度Aj為

整個裝備的備件保障度As為

(10)

第i類裝備的使用可用度Aoi為

Aoi=A′o·As

(11)

式中：A′o為裝備的固有可用度。

合成部隊多型號裝備群的使用可用度A為

(12)

式中：N為裝備類型總數；αi為合成部隊不同型號裝備對于整個裝備系統體系的貢獻率，其權重值可由專家打分法確定，且∑αi=1。

4 優化模型及算法

4.1 考慮任務演化重要度的器材配置優化模型

裝備使用可用度在保障資源不受限的條件下可隨備件保障度的提高而滿足指揮員不同目標要求。當部隊遂行作戰或演習駐訓任務時則不能無限制地攜行全部器材，必然受運輸車存儲空間、車載質量、保障費用等綜合因素的制約。此外，部隊應優先攜行對裝備系統功能狀態影響較大的重要器材。因此本文在器材配置優化求解過程中，除考慮車載體積、車載質量、保障費用等基本約束條件外，將任務演化重要度納入器材配置優化目標函數建模中。故兩級維修器材配置優化模型為

(13)

式中：kj為第j個可更換單元的任務演化重要度；Vj為第j個可更換單元的體積；Mj為第j個可更換單元的質量；Cj為第j個可更換單元的費用；Vs為當前器材配置方案最大體積；Ms為當前器材配置方案最大質量約束；Cs為維修器材總費用約束。

4.2 模型求解

合成部隊維修器材兩級配置方案的目標函數是使裝備的備件保障度最大，并突出重要部件備件保障度權重酌情增大的現實特點。本文針對多約束方程式(13)利用邊際分析法[18]進行器材配置方案的優選。

邊際分析法是METRIC、OPUS軟件等核心算法，屬于典型的貪婪算法，其核心思想是比較不同種器材在不同級別每增加一個器材的效益值增量ΔA/z(z為約束值，如費用、體積、質量等)，從而確定選擇增加哪一類器材。邊際分析法要求效益函數為凸函數，本文影響器材配置優化的因素為多個變量，必須將多個變量轉化為單變量約束才能繼續使用邊際分析法，因此首先進行多約束變單處理，引入拉格朗日算子，將3個影響因素轉換為復合約束zj，具體表示為

zj=λVVj+λmmj+λccj

(14)

式中：λV、λm、λc分別為體積、質量、費用在復合約束zj中的權重因子；Vj、mj、cj分別為第j類可更換單元的體積、質量和費用。根據實際情況可設置任一權重因子值為零，將多約束條件轉化為單一約束；也可設置各個權重因子不為零，將其他因素等效轉化為單一復合約束。此時，可將式(10)寫為

(15)

令當前器材資源組合為Zj=(z1,z2,…,zj，…,zn)，在此基礎上為第j類器材增加一個備件后器材資源組合為Z′j=(z1,z2,…,z′j,…,zn)，對式(15)等號兩端取對數，可得

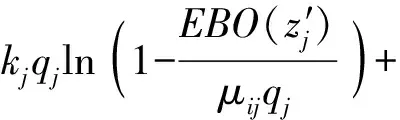
(16)

根據邊際分析算法在每輪迭代過程中得到的收益(備件保障度增量)除以成本值(復合約束zj)，得到邊際效應值δ：

(17)

通過式(17)分別計算出本級和上級器材倉庫在每一輪迭代中每項器材增加的邊際效應值δ，將最大值δ所對應的該級別庫存該類器材數量加1，依此循環，直到滿足所有指標約束后，算法結束。此時得到滿足多約束條件下的最優兩級維修器材配置方案為

(18)

4.3 約束因子初始化及調整更新

由于器材體積、質量、費用對模型優化影響不同，在進行優化計算之前，需要首先合理確定體積因子λv、質量因子λm、費用因子λc的初始值，分別記作λv0、λm0和λc0，其確定方法如下：

1)只考慮單一因素影響如只關注體積，不再考慮其他約束影響時，令λv=1，λm0=0，λc0=0，通過邊際分析計算得到一組初始最優器材配置方案s0=(s1,s2,…,sj,…,sn)；

2)計算該器材配置方案s0下所對應的器材總體積、總質量和總費用V(s0)、M(s0)、C(s0)，并重新計算初始約束因子λm0、λc0，計算方法如下：

(19)

將式(19)代入式(14)，再次利用邊際分析法進行迭代尋優，得到另一組器材配置方案s=(s1,s2,…,sj,…,sn)。若該方案所對應的器材總質量、總費用中任何一個約束超過設定指標，則需要增加該約束的權重因子值。其增量計算如下：

(20)

式中：Ms、Cs分別為設定的約束指標值。若得到的配置方案所對應的質量、費用仍然超過了設定的指標，則可以在當前約束指標權重基礎上，通過式(20)對其數值動態調整。當然可能會出現一種特殊的情況，在既定的備件體積、質量和費用約束下無論怎樣調整權重因子也不能得到一組滿足所有約束條件的解，在此情況下就需要重新設定條件，可適當降低備件保障度目標指標或增加質量約束、體積約束指標。

3)同樣也可根據指揮員經驗，判斷各個約束對于任務完成結果的影響程度來確定權重因子的判定規則，例如根據指揮員分析判斷，各約束因子權重應滿足以下規則：

λv≥λm≥λc

(21)

該判定規則反映出體積約束是指揮員認為限制本次任務順利達成首要考慮的因素，質量、費用為次要因素。在優化計算過程中，若器材總體積V(s0)超過約束條件Vs，則需動態調整其他約束因子λm和λc。調整前首先比較當前權重因子是否符合指揮員的判定規則，只需對違反規則的權重因子進行調整。這里以λm0<λc0為例，僅需更新λm的計算，λc保持不變，此時令λm=Vsλm0/V(s0)，再利用邊際分析法進行迭代尋優，得到另一組器材配置方案。

4.4 基于MA-OD目標分解的邊際分析法算法設計

傳統邊際分析法通過反復迭代能夠尋求滿足目標的最優庫存方案解，使得指揮員可依據設定指標對器材配置方案進行分析和選擇，該算法簡便直觀，易于實現。但隨著器材品種、保障體系多級庫存機構數量的增多，維修器材的多級多約束配置優化就會演變為大規模、非線性NP難問題，模型算法的執行效率會大幅下降，以模型決策變量為m個站點i種器材的庫存量集合矩陣Sm×n為例，采用傳統邊際分析法計算時需迭代的次數G=m∑nj∑si[24]。

為提高運算效率，有效解決數據規模空間急劇增長的實際問題，本文提出一種基于目標分解(MA-OD)的邊際分析算法。該算法沿用分層優化的思想[9]對傳統邊際分析法進行分層改進，首先進行從裝備使用可用度到部件平均可用度的分層折算，同時兼顧不同部件任務演化重要度不同的特點，將模型目標函數按重要度分解為不同種類的備件保障度目標描述以突出重要器材重點保障的原則；最后，通過迭代的過程完成所有類別器材的優化配置，該算法的預計迭代次數為N=m∑nj·si。具體求解步驟如下：

步驟1分層初始化。根據裝備使用可用度指標Ao確定其所屬的各項部件初始平均可用度A′oj：

(22)

步驟2按部件任務演化重要度分解目標備件保障度Aoj。按照式(10)可知裝備的使用可用度和所屬部件備件保障度線性相關，考慮各個部件重要度不同，要保證A≥Ao，各個部件的備件保障度可因任務演化重要度酌情調整，以此作為后續器材合理配置數量的目標依據。設Kj為第j個可更換單元的任務演化重要度，各個部件的目標備件保障度Aoj計算如下：

(23)

由于在相同任務階段下部件任務演化重要度評價等級(重要、次重要、不重要)區別差距不大，即能保證A≥Ao。

步驟3采用邊際分析法分別對各項部件進行優化計算，得到關于各項部件的目標- 約束曲線圖。

步驟4擬合裝備使用可用度曲線，驗證各部件的目標備件保障度Aoj乘積：∏Aoj≥Ao，則算法結束，得到器材配置優化方案。具體流程如圖5所示。

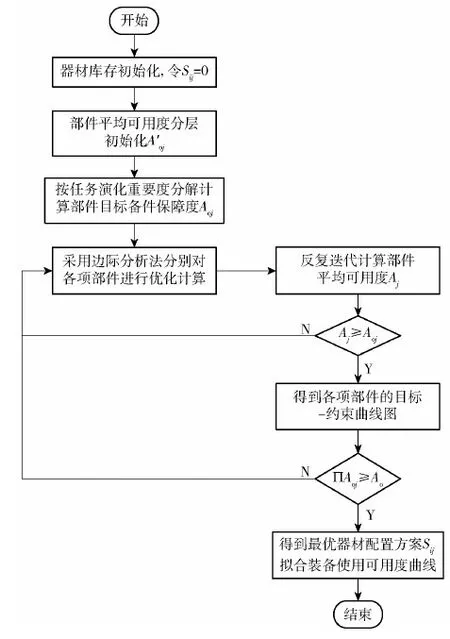
圖5 MA-OD算法流程Fig.5 Algorithm flow of MA-OD

5 算例分析

5.1 任務想定

以某集團軍對西部方向遂行封控作戰演習任務為例，上級決定將合成1旅、合成2旅、合成3旅組成前沿作戰群。按照上級命令，要求前沿作戰群按時機動至集結地域，并滿足部隊裝備使用可用度不低于95%的要求。為保障該部隊裝備完好性和任務成功率，需在運力受限條件下合理規劃攜行維修器材配置方案，使得該部隊裝備的使用可用度最大。已知3個合成旅部隊編制、裝備實力基本相當，主要以自我保障和上級保障兩種方式實施裝備維修保障，預計本級器材倉庫平均請領周轉時間為3 h，上級平均修復故障件時間為2 h，上級平均籌措器材時間為50 h，部隊在戰斗實施階段時主要編配3種型號裝備負責重點任務的達成，其裝備主要系統可靠性框圖如圖6所示，相關參數見表1。假設部隊在任務實施過程中裝備損壞事件服從泊松過程，現以上述背景對該群進行軍旅兩級維修器材配置方案規劃。

圖6 戰斗實施階段下合成部隊裝備群構成Fig.6 Composition of the equipment group of the synthetic force during conduct of combat

5.2 解算流程

首先依據該任務階段裝備系統組成見圖6，計算裝備群在戰斗實施階段下各部件的任務演化重要度，計算方法見下述計算，得出所屬裝備各部件的重要度分值及排序如表2所示。

參照裝備1系統可靠性框圖計算各部件的任務演化重要度為

參照裝備2系統可靠性框圖計算各部件的任務演化重要度為

表1 所屬部隊裝備相關參數Table 1 Equipment related parameters

表2 戰斗實施任務下裝備部件重要度分值Table 2 ScoringTable for the importance of equipment components under combat implementation tasks

參照裝備3系統可靠性框圖計算各部件的任務演化重要度為

本例采用第2種考慮裝備體系貢獻率的方式，對實際任務演化重要度打分和歸一化處理；為滿足指揮員對整個任務期間裝備使用可用度要求不低于95%的目標，現結合部隊實際運力載荷要求，分別以費用、體積、質量為約束，采用前文所述優化模型和算法求解滿足要求的器材配置優化方案。

根據模型求解步驟，首先按照傳統邊際分析法只考慮單一約束如體積，確定初始約束因子，令λv=1，λc=λm=0，即不考慮器材其他約束時，通過優化計算得到一組攜行器材配置方案s0(3，1，2；4，1，1；5，0，0，1)。在該方案下，裝備使用可用度A(s0)為95.8%，器材費用C(s0)為103.3萬元，器材體積V(s0)為29.755 m3，器材質量M(s0)為5 207.44 kg。使用該數據計算得到初始體積、質量約束因子值：

根據規定通用運輸車體積約束指標30 m3，質量約束指標5 t，在僅考慮器材體積約束時，此配置方案s0不能滿足運輸車載荷要求。需引入初始約束因子λm0、λc0得到綜合約束因子值zj，經迭代計算得出另一組器材攜行配置方案s(3，1，1；4，1，1；4，1，1，1)，該方案下裝備可用度為95.5%，器材費用為97.58萬元，器材質量為4 950.4 kg，器材體積29.93 m3，該配置方案滿足各項指標要求，因此方案s為最終優化配置方案。

5.3 結果分析

依據不同目標要求動態調整各約束因子值，可以實現不同目標、約束條件下最優兩級器材配置方案見表3，具體方案結果和指標描述見表4，各配置方案目標- 約束迭代變化曲線如圖7所示。

表3 多維目標- 約束下器材配置方案比較Table 3 Comparison of spare parts allocation schemes under different constraint conditions

表4 多維目標- 約束下器材配置方案結果對比Table 4 Comparison of the results of spare parts allocation schemes under different constraints

圖7 不同目標- 約束迭代曲線圖Fig.7 Objective-constraint relationships under different constraint condition

根據表3所示的各類配置方案，可以從不同維度得出各方案所對應的裝備使用可用度，具體結果見表4。對比分析各類配置方案可知：在5種方案中，當僅考慮單一約束進行方案求解時如體積方案1，所得方案不能滿足所有約定條件；當考慮綜合約束時所得方案符合要求，但因考慮目標、約束條件側重角度不同，器材配置方案有所不同，所達成的目標效果也有所不同。具體分析如下：

1)分析各類方案可知：方案1為僅考慮單一體積約束得出的器材配置方案，相比而言體積較大的部件比同等條件下的其他部件配置量較少；方案2是考慮綜合約束條件下的器材最優配置方案，各類器材配置數量普遍介于單一約束方案下的極值配置數量之間。這類方案不僅滿足器材運力載荷要求，也可兼顧指揮員經驗規則，通過動態調整各個約束權重因子值，最終得到滿足指揮員基于任務成功影響決策偏好的軍事目標方案；方案3是考慮部件任務演化重要度不同得出的器材配置方案，對于同等條件下故障率較高且較為重要的部件配置量相對增加，這種方案改變了傳統可用度模型中將部件重要度同等對待的構建思路，在器材配置策略上可以做到重要器材重點保障，同時兼顧一般器材，裝備使用可用度比未考慮重要度下綜合約束配置方案有所提升；方案4與方案5是從費用管理的角度考慮綜合約束和部件重要度的兩類配置方案，與其他方案對比，這兩類方案可以在滿足約束條件的基礎上有效降低器材配置費用，這對優化平時部隊器材配置費效比也有一定的指導意義。

2)分析配置方案約束- 目標迭代曲線(見圖7)，曲線上任意一點都描述了當前約束條件下的最優結果，這里以考慮單一約束—體積為例，當裝備使用可用度達到其規定的指標95%時，器材總體積為28.95 m3，因此設定的器材體積約束指標必須滿足Vs≥28.95 m3，如果Vs不能滿足28.95 m3，就必須調整可用度指標，以通過降低可用度來滿足體積約束條件。

3)通過對比分析兩級庫存器材配置方案可以發現：以備件保障度為目標的維修器材兩級動態配置模型可有效降低因備件保障延誤對裝備使用可用度產生的風險影響。特別對于故障率高、本級修理率偏低且存在一定報廢率的可修部件，在不考慮其他影響裝備停機情況如維修時間長、等待維修人員、維修機工具等因素下，產生備件延誤的關鍵因素在于上級器材庫存得到備件的時間。因此，當作戰部隊規模較大時，兩級維修器材動態配置模型能夠有效縮短備件短缺延誤時間從而提高裝備使用可用度。從一定意義上來說，這種配置模式比較貼近現行軍旅兩級部隊現實需求和裝備維修保障實際，與戰時軍旅兩級維修保障體系下維修保障任務區分、力量編組、資源配置的實際運行情況較為一致。因此，加強陸軍合成部隊維修器材兩級配置優化研究對于降低器材保障不確定性、提升部隊裝備使用可用度和任務成功率具有一定的指導意義。

6 結論

本文以面向合成部隊維修器材兩級配置優化研究為背景，針對不同任務階段部件功能狀態對裝備系統功能狀態影響程度不同建立了裝備部件的任務演化重要度模型，相比傳統模型更加注重部件重要度的區分對待。以基于任務演化重要度的備件保障度為目標，構建了合成部隊維修器材兩級動態配置優化模型，通過引入拉格朗日算子求解出符合多約束條件的最優配置方案。最后以某合成部隊遂行典型任務為例進行了算例驗證。結果表明，本文構建的考慮任務演化重要度的兩級維修器材配置模式在資源受限時特別是戰時比較貼合部隊現實需求和裝備維修保障實際，該模式為陸軍合成部隊開展維修保障資源優化配置提供了新的理論指導，對于提高裝備可用度和任務成功率具有一定的指導意義。