多源數據下的檢測器布設及交通需求估計研究
陳 輝
(中交第二公路勘察設計研究院有限公司,江蘇 南京 210012)
0 引言
交通需求是城市居民出行分布的集計,其準確性決定了城市交通規劃與管理決策方案的科學性。當前城市交通系統可監測多源數據,這些多源數據給城市交通需求的準確估計帶來了新的方向和挑戰[1]。
近年來,學者們運用多種理論對交通需求進行估計。主要研究方法包括:廣義最小二乘法[2]、指數平滑預測法[3]、貝葉斯估計方法[4]、基于公交卡數據預測法[5]、基于手機應用軟件數據預測法[6]等。網絡檢測器布局問題作為交通需求的子問題,可以用來識別檢測器布設位置,以確定唯一的未觀測路段流量或者最優化待估交通需求的質量。為獲得唯一的未觀測路段流量,欒鑫等[7]利用成本和出行可靠性建立檢測器布設模型;董春肖等[8]分析檢測器布設位置對交通流量預測的影響;Fu等[9]提出多種類型檢測器布設方案;Salari等[10]考慮檢測器對交通需求估計的影響程度;孫超等[11]進一步提出了路徑流量最大覆蓋率準則。
盡管上述文獻運用不同方法對檢測器布局策略和交通需求估計進行了研究,但仍然存在一些不足:①已有文獻沒有使用多源數據融合技術進行交通需求估計。②對交通檢測器布局的研究沒有綜合考慮路段和路徑流量的覆蓋信息。③缺乏從交通網絡理論角度推導交通需求與流量之間的解析關系,該關系有助于建立最大似然交通需求估計模型。為此,該文提出檢測器布局和最大似然交通需求估計整合模型。前者通過最大化路段和路徑覆蓋信息來計算最優檢測器布局數量和位置,同時采用最小方差加權平均技術對檢測的多源數據進行融合,從而運用最大似然法估計交通需求,并設計迭代算法求解模型。
1 檢測器布設及交通需求估計
1.1 檢測器布局模型
交通需求估計可被視為數學中的參數估計問題:觀測部分樣本(如道路流量、速度、密度、旅行時間等)來估計總體分布中的參數(即交通需求)。在既有預算下,觀測哪些路段樣本以估計出最可靠或最符合實際的交通需求,是該文需解決的前提性科學問題。
通過研究檢測器布局模型來確定最優的檢測器布設數量和位置,已有檢測器布局模型單方面最大化路段覆蓋信息或路徑覆蓋信息。該文在給定預算下,同時最大化路段和路徑覆蓋信息:
約束條件:
式中,W——路網OD對集;ω——其中的一個OD對;Kω——OD對ω之間所有路徑的集合,k∈Kω;α——權重系數;——路段a上的先驗流量;——OD對ω間路徑k上的先驗流量;——OD對ω間路徑k上的覆蓋系數,如果路徑k上存在某個路段布設了檢測器,該參數為1,否則為0;s——檢測器數量;bs——檢測器安裝費用;bmax——總預算;za——路段a上的覆蓋系數,如果路段a上布設了檢測器,該參數為1,否則為0;A——路段集,a∈A;——在OD對ω間,如果路段a在路徑k上,該參數為1,否則為0。
1.2 多源觀測變量融合
觀測檢測器布設位置上的交通量、旅行時間、速度等數據,由于觀測變量間的量綱不一致,采用交通流理論對觀測變量間的量綱進行轉換,從而統一化觀測的多源路段信息。該文采用交通流三參數理論將多源觀測變量統一為路段流量:
式中,va——路段a上的交通量;ta——路段a上估計的旅行時間;la——路段a的長度;Mj,a——路段a上的擁擠密度;Sf,a——路段a上最大行駛速度。
運用最小方差加權平均方法對多源數據進行融合:
1.3 最大似然交通需求估計模型
采用泊松分布描述隨機交通需求qω:Pois(d ω),交通需求近似服從如下多元正態分布形式:
式中,d ——交通需求的均值向量形式,即d ={… ,dω,…}。該文假設交通需求之間相互獨立,因此交通需求的協方差矩陣為 Λ= d iag (d)。在隨機用戶均衡模型中:
式中,——OD對ω間路徑k上的流量;Pr(·)——概率算子;cω——路徑旅行時間的向量形式,即對ω間路徑k上出行用戶路徑選擇概率:
式中,θ——出行者感知誤差程度;——OD對ω間路徑k上估計的路徑旅行時間。因此路徑流量也服從多元正態分布形式:
式中,V ——所有路段流量的向量形式,即V={… ,va,…},va——路段a上的交通流量;A表示路段集;Δ=()為路徑 — 路段關聯矩陣。
根據融合后的觀測路段流量(式8)和路段流量與交通需求之間的解析關系(式13),建立交通需求的似然函數:
式中,g(·)——概率密度方程。由前面可知,路段流量V 的對數似然函數為:
基于融合技術,即式(8)獲得的路段流量,運用雙層規劃理論建立最大似然交通需求估計模型,其中上層模型利用最大似然法求解交通需求,下層為SUE模型求解路徑選擇概率。
上層:
下層:用SUE模型(即式10)分配交通需求d,從而獲得路徑選擇概率p 。
2 算法設計
在檢測器布設過程中設計了逐次識別檢測器算法,在求解最大似然交通需求估計模型時,運用迭代算法框架反復計算上層和下層模型。獲得的檢測器布設數量和位置,觀測這些位置上的交通量、旅行時間、速度等,運用式(8)對這些觀測變量進行融合,進而運用迭代算法估計交通需求。
步驟1 初始化:設置迭代步數n=0;收斂精度ε;交通需求的均值d(0),因此交通需求的協方差矩陣為Λ= d iag (d(0)),同時初始交通需求設為d(0);融合后的路段流量。
步驟2 求解下層模型:運用相繼平均算法分配需求d(n),從而獲得路徑選擇概率p(n)。
步驟3 求解上層模型:代入路徑選擇概率p(n),采用最速下降算法獲得過渡交通需求。
3 算例分析
Nguyen-Dupuis城市路網[12]其拓撲結構、路段屬性和交通需求量如圖1、表1、表2所示,運用BRP函數來表示路段阻抗,其中ta——實際出行時間;——自由出行時間;xa——流量;Ca——通行能力;β=0.15和n=4為確定參數。
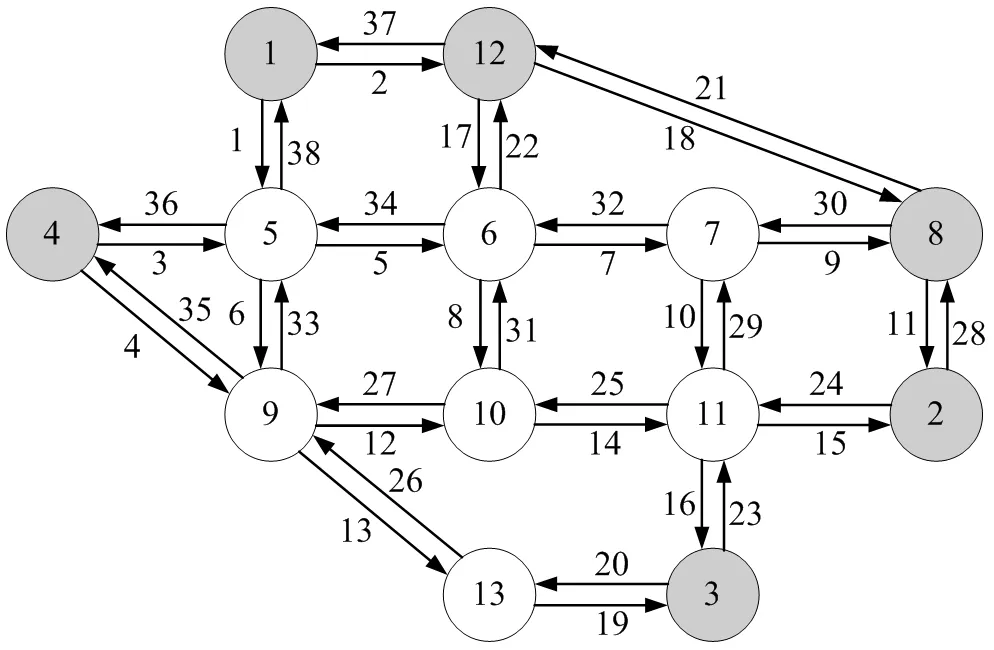
圖1 Nguyen-Dupuis網絡拓撲結構

表1 Nguyen-Dupuis網絡路段屬性
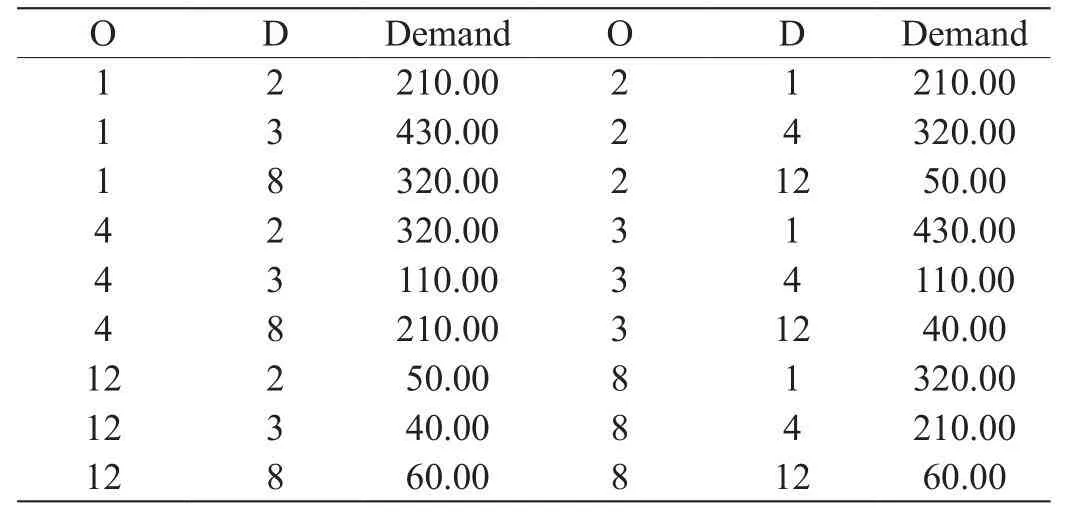
表2 Nguyen-Dupuis網絡OD需求
權重系數設為α=0.5,路段檢測器(路段速度)最大布設數量smax=6。圖2描繪了隨檢測器布局位置逐一識別后,三種模型(目標函數僅考慮路段覆蓋信息:;該文檢測器布局模型;目標函數僅考慮路徑覆蓋信息:目標函數值的變化情況。從圖中可以發現,三種模型下的目標函數值均隨著檢測器識別數量的增加而增加。與傳統檢測器布局模型相比,該文提出的檢測器布局模型同時利用了路段和路徑兩方面的覆蓋信息,可以獲得可靠性更高的檢測器布設方案。
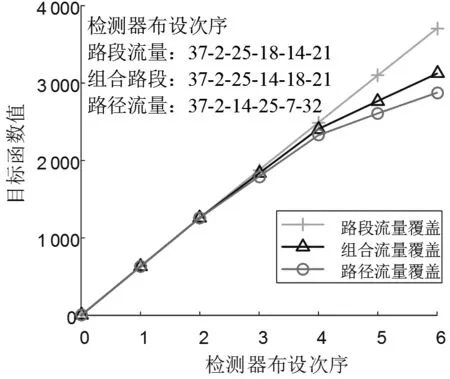
圖2 目標函數值隨檢測器逐次識別變化圖
根據圖2中的檢測器位置,觀測路段37、2、25、14、18和21上的多源數據,其值為SUE模型分配交通需求均值所得,進一步根據式(8)對這些觀測交通變量融合。從圖3中可以發現當觀測數據擾動都為0%時,交通需求的均方根誤差接近0。且均方根誤差隨著觀測數據擾動的增加而增大,這意味輸入參數的擾動對交通需求的估計產生顯著影響。
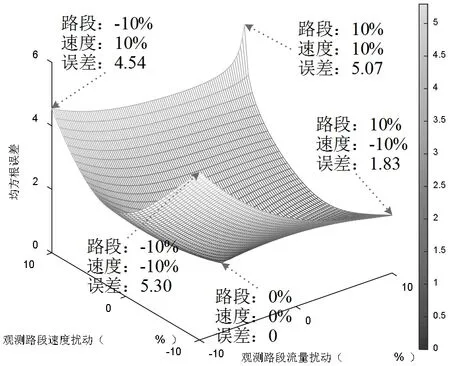
圖3 觀測數據對交通需求擾動分析
4 結語
為獲取城市路網規劃與交通管控的基礎數據,利用現代信息技術觀測的多源數據建立了檢測器布局模型和最大似然交通需求估計模型,并設計了迭代算法求解建立的模型。
路網測試結果表明:同時考慮路段和路徑兩方面覆蓋信息的檢測器布局方案更具可靠性;輸入參數的擾動對需求估計產生顯著影響;設計的算法可以快速收斂于均衡解;多源數據融合下的交通需求估計方法通過充分挖掘觀測數據信息,從而估計出與實際值相接近的交通需求。在后續研究中,將進行擁堵網絡中動態交通需求估計,并進一步運用估計的交通需求對城市路網進行規劃。

