“雙棒”在磁場中運動問題分類剖析

■福建省漳州招商局經濟技術開發區海濱學校 周乾坤

“雙棒”在磁場中運動問題涉及電磁感應和電路的綜合應用,遇到“雙棒”在磁場中的運動問題,只要抓住“單棒”切割磁感線產生的感應電動勢E=BLv,“雙棒”切割磁感線產生的總感應電動勢可以同向串聯或反向串聯,以及閉合電路歐姆定律,即可順利求解。下面選取常見的兩類“雙棒”在磁場中的運動問題,探究其求解方法,供同學們參考。

一、“雙棒”在水平導軌上運動

兩根導體棒與水平導軌組成閉合回路,兩根導體棒做切割磁感線運動,產生感應電動勢,形成雙電源問題。求解這類問題時,分析感應電動勢的大小是關鍵環節,可以先求出初、末二態磁通量的變化量,再運用法拉第電磁感應定律求出總感應電動勢;也可以先求出每一根導體棒產生的感應電動勢,再根據兩感應電流的方向相同,兩感應電動勢取和,兩感應電流的方向相反,兩感應電動勢取差,求出總感應電動勢。

1.“雙棒”在水平導軌上同向運動。

例1兩根足夠長固定平行金屬導軌位于同一水平面內,導軌上垂直放置兩根導體棒1和2,在整個導軌平面內有豎直向上的勻強磁場,其俯視圖如圖1 甲所示。已知兩導軌間的距離為L,兩根導體棒的質量均為m,電阻均為R,回路中其余部分的電阻不計,勻強磁場的磁感應強度為B。兩導體棒與導軌接觸良好且均可沿導軌無摩擦地滑行,開始時兩導體棒均靜止,間距為x0。現給導體棒1向右的初速度v0,并開始計時,得到如圖1乙所示的Δv-t圖像,其中Δt=v1-v2,v1表示導體棒1 的瞬時速度,v2表示導體棒2 的瞬時速度,則下列說法中正確的是( )。

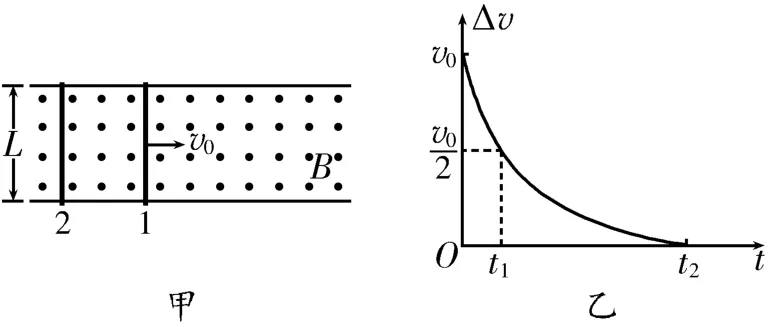
圖1

A.在0～t2時間內,回路中產生的焦耳熱

B.t1時刻回路中的感應電動勢E=BLv0

C.t1時刻導體棒2 的加速度a=

D.t2時刻兩導體棒間的距離x=x0+

解析：根據F安=BIL可知,兩導體棒所受安培力等大反向,由兩導體棒組成的整體不受外力作用,動量守恒。t2時刻Δv=v1-v2=0,說明兩導體棒同速,根據動量守恒定律得mv0=(m+m)v,解得,根據能量守恒定律得,解得,選項A 正確。t1時刻Δv=v1-,根據動量守恒定律得mv0=mv1+mv2,解得。t1時刻兩導體棒均向右做切割磁感線運動,形成雙電源,根據法拉第電磁感應定律得E=BLv1-BLv2,其中,解得,根據閉合電路歐姆定律得,對導體棒2應用牛頓第二定律得BIL=ma,解得a=,選項B錯誤,C正確。在0～t2時間內,對導體棒2應用動量定理得,即,又有,解得x=,選項D 正確。

答案：ACD

點評:在0～t2時間內,導體棒1向右做初速度為v0的減速運動,導體棒2由靜止開始向右做加速運動,根據右手定則判斷出兩導體棒中的感應電流方向相反,且導體棒1的速度大于導體棒2的速度,導體棒1 切割磁感線產生的感應電動勢較大,因此回路中的總感應電動勢E=BLv1-BLv2。

2.“雙棒”在水平導軌上反向運動。

例2兩根足夠長固定平行金屬導軌位于同一水平面內,導軌上垂直放置兩根金屬棒,在整個導軌平面內有豎直向下的勻強磁場,其俯視圖如圖2所示。已知兩導軌間的距離d=0.2 m,勻強磁場的磁感應強度B=0.2 T,兩根金屬棒的電阻均為r=0.25 Ω,回路中其余部分的電阻不計。兩根金屬棒在平行于導軌的拉力作用下沿導軌朝相反方向勻速平移,速度大小均為v=5 m/s,兩根金屬棒與導軌接觸良好,不計金屬棒與導軌之間的摩擦。在兩根金屬棒的間距增加s=0.4 m 的滑動過程中,下列說法中正確的是( )。

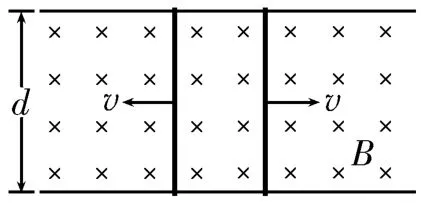
圖2

A.每根金屬棒切割磁感線產生的感應電動勢均為E=0.2 V

B.回路中的感應電流I=0.4 A

C.作用在每根金屬棒上的拉力大小F=3.2×10-2N

D.回路中產生的熱量Q=2.56×10-2J

解析：兩根金屬棒同時沿導軌朝相反方向勻速平移,兩根金屬棒切割磁感線產生的感應電動勢大小相等,方向相同,兩根金屬棒與導軌構成閉合回路,其等效電路如圖3所示。根據法拉第感應定律得每根金屬棒切割磁感線產生的感應電動勢大小E1=E2=Bdv=0.2 V,根據閉合電路歐姆定律得回路中的感應電流,選項A 正確,B錯誤。金屬棒沿導軌勻速移動,受到的拉力等于安培力,則F=F安=BId=3.2×10-2N,選項C 正確。在兩根金屬棒的間距增加s=0.4 m 的滑動過程中,回路中產生的熱量等于兩根金屬棒克服安培力做功而轉化的電能,也等于外力F做的總功,則Q=,選項D 錯誤。

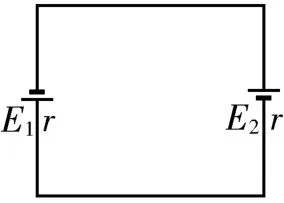
圖3

答案：AC

點評:兩根金屬棒沿導軌朝相反方向勻速平移,根據右手定則判斷出兩根金屬棒中的感應電流方向相同,兩根金屬棒切割磁感線產生的感應電動勢之和等于閉合回路的總感應電動勢。

注意：在兩根金屬棒的間距增加s的滑動過程中,每根金屬棒的位移均為,而不是s。

二、“雙棒”在不同面導軌上運動

兩根導體棒與不在同一個平面內的導軌組成閉合回路,不僅要考慮導體棒切割磁感線產生的感應電動勢,還要考慮動能、勢能、內能之間的轉化關系。求解這類問題時,一般情況下需要將兩根導體棒視為一個整體,靈活選用動量定理、動量守恒定律、能量守恒定律等物理規律列式求解。

例3如圖4所示,半徑為r的光滑四分之一圓弧軌道MN、M'N'與足夠長的水平光滑金屬軌道NP、N'P'平滑連接,兩軌道等高且平行,軌道間距為L,電阻不計。電阻為R,質量為m的金屬棒cd鎖定在水平軌道上距離NN'連線足夠遠的位置,整個裝置放在磁感應強度大小為B,方向豎直向上的勻強磁場中。現在外力作用下使電阻為R,質量為m的金屬棒ab從軌道最高端MM'位置開始以大小為v0的速度沿圓弧軌道做勻速圓周運動,金屬棒ab在運動過程中始終與軌道垂直且接觸良好,重力加速度為g,則( )。

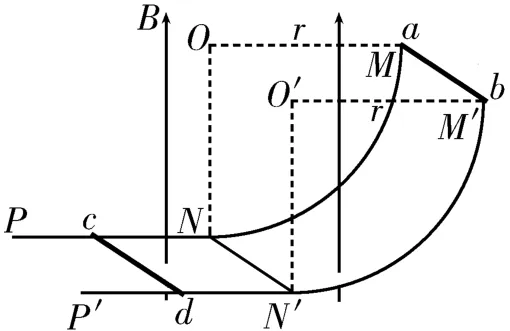
圖4

A.金屬棒ab剛好運動到NN'連線位置時金屬棒cd受到的安培力大小為,方向水平向左

B.金屬棒ab從MM'連線位置運動到NN'連線位置時,回路中產生的焦耳熱為

C.若金屬棒ab運動到NN'連線位置時撤去外力,則金屬棒ab沿軌道能夠運動的距離為

D.若金屬棒ab運動到NN'連線位置時撤去外力并解除金屬棒cd的鎖定,則從金屬棒ab開始運動到最后達到穩定狀態的整個過程中,回路中產生的焦耳熱為

解析：金屬棒ab剛好運動到NN'連線位置時,回路中的瞬時電流,金屬棒cd受到的安培力大小,方向水平向左,選項A 正確。金屬棒ab從MM'連線位置運動到NN'連線位置的過程中做勻速圓周運動,設金屬棒ab運動到圓弧軌道上的某位置時,該位置與圓心連線跟水平方向之間的夾角為θ,根據v0t=rθ可得,感應電動勢,因此回路中電流的有效值,又有金屬棒ab沿圓弧軌道運動的時間,故回路中產生的焦耳熱,選項B 錯誤。從撤去外力到金屬棒ab停止運動的過程中,根據BILt=mv0和,解得x=,選項C 錯誤。金屬棒ab運動到NN'連線位置時撤去外力并解除金屬棒cd的鎖定,從撤去外力到兩金屬棒達到穩定狀態的過程中,根據動量守恒定律得mv0=2mv,根據能量守恒定律得,解得。因此從金屬棒ab開始運動到兩金屬棒達到穩定狀態的過程中,回路中產生的焦耳熱Q=Q1+Q2=,選項D 正確。

答案：AD

點評:金屬棒ab沿圓弧軌道下滑,金屬棒cd鎖定時,金屬棒ab切割磁感線產生正弦式感應電動勢,計算回路中產生的焦耳熱應代入感應電流的有效值。金屬棒ab運動到NN'連線位置時撤去外力并解除金屬棒cd的鎖定后,兩根金屬棒在水平軌道上平動,滿足動量守恒定律和能量守恒定律。