高考物理模擬試題(一)參考答案與提示
1.C 提示:目前世界上的核動力航母利用的是重核的裂變,選項A 錯誤。提高溫度不可以改變放射性元素的半衰期,選項B 錯誤。盧瑟福發現質子的核反應方程是,選項C 正確。發生核反應時滿足質量數守恒和電荷數守恒,質量會有虧損,選項D 錯誤。
2.B 提示:小球被拋出后做平拋運動,根據平拋運動規律得,解得,選項A 錯誤。火星的第一宇宙速度即近火衛星的運行速度,則,選項B 正確。以位于火星表面的物體為研究對象,則mg,解得火星的質量,選項C錯誤。火星的平均密度,選項D 錯誤。
3.C 提示:選O點為研究對象,進行受力分析,如圖1所示,根據平衡條件得Tacosθ1+Tbcosθ2=Tc,Tasinθ1=Tbsinθ2,又有Ta=mag,Tb=mbg,Tc=mg,ma=300g,mb=500g,根據數學知識得θ1>θ2,m>400g。
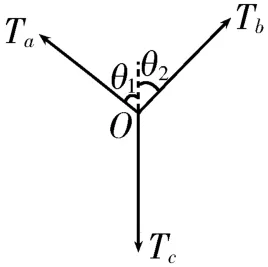
圖1
4.A 提示:子彈射入木塊的時間極短,瞬間動量守恒,根據動量守恒定律得mv0=(M+m)v,解得。木塊自被子彈擊中前到第一次回到原來位置的過程中,根據動量定理得木塊受到的合外力的沖量大小。
5.C 提示:若粒子從ab邊中點處垂直于ab邊射出,則其運動軌跡的圓心一定在ab邊上,設圓心與ab邊的交點為g,則圓心在Og連線的中垂線上,而該中垂線與ab邊平行,不可能相交,選項A 錯誤。粒子從a點垂直于af邊射出,f點為其運動軌跡的圓心,對應的圓心角為60°,因此粒子在磁場中的運動時間,又有,解得,選項B 錯誤。垂直于cf連線向上發射的粒子剛好能離開磁場時,其運動軌跡與af邊相切,根據幾何關系得,根據qvB得,解得,選項C 正確。因為O點距磁場正六邊形邊界的最近距離,即d對應粒子剛好離開磁場的運動軌跡的最小直徑,所以粒子運動軌跡的最小半徑,又有,解得,選項D 錯誤。
6.BD 提示:小球沿直線AB運動,受到的合外力沿AB方向,小球的受力情況如圖2所示,則qEtan 45°=mg,解得,選項A錯誤。小球所受合外力,根據勻變速直線運動規律得小球到達B點時的速度v=,根據牛頓第二定律得加速度。設A、B兩點間的距離為L,根據動能定理得,解得靜電力做功。根據W=qUAB,解得。根據UAB=φA-φB,且A點的電勢為零,解得φB=,則B點的電勢能EB=qφB=,選項B 正確,C 錯誤。小球機械能的變化量等于靜電力做的功,則ΔE=W=,選項D 正確。
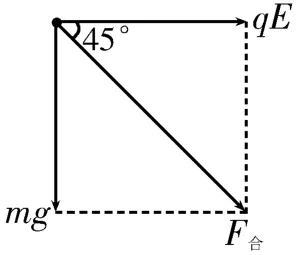
圖2
7.CD 提示:根據u-t圖像得輸入電壓的周期T=0.02 s,則,輸入電壓的最大值Umax=20 2 V,因此輸入電壓的瞬時值表達式為u=20 2sin(100πt) V,選項A 錯誤。只斷開開關S2后,負載電阻增大為原來的2倍,副線圈電壓不變,則副線圈中的電流減小為原來的一半,燈泡L1、L2的功率均變為額定功率的四分之一,即燈泡L1、L2均不能正常發光,選項B 錯誤。只斷開開關S2后,負載電阻變大,副線圈中的電流變小,輸出功率變小,則原線圈的輸入功率減小,選項C正確。將開關S1換接到2后,電阻R兩端電壓的有效值為4 V,則電阻R消耗的電功率,選項D正確。
8.AD 提示:細桿由靜止運動至細桿前端到達C點的過程中,根據動能定理得,解得,選項A 正確。細桿前端過C點后,在C點右側的部分受到摩擦力作用,設桿長為l,C點右側部分的長度為x,則,解得。又有細桿受到的摩擦力f=μN=μm'g=,根據牛頓第二定律得a=。當細桿后端過C點后,細桿受到的摩擦力f=μmg,解得a=μg,保持不變。因此細桿受到的摩擦力f隨x變化的圖像如圖3所示,即細桿先做加速度變大的減速運動,后做勻減速運動,選項B錯誤。取細桿左側長為x0的一段為研究對象,當細桿全部進入C點右側時,有,對整體有μmg=ma,則μm1g-F=m1a,解得F=0,即細桿前后兩段間無彈力。當細桿左側長為x0這段還沒全部進入C點右側時,有,解得。對細桿左側長為x0這段有F=m1a≠0,可見細桿前一段對后一段的作用力大小不等,選項C錯誤。細桿從其前端過C點到全部進入C點右側的過程中,有,細桿從全部進入C點右側到停止運動的過程中,有。根據動能定理得,解得,選項D正確。
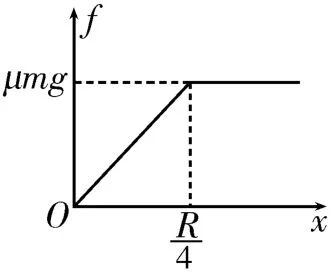
圖3
9.(1)×1 k (2)+插孔 -接線柱(3)1 900 1.7 (4)如圖4所示 (5)4.7 kΩ 0.59 mA
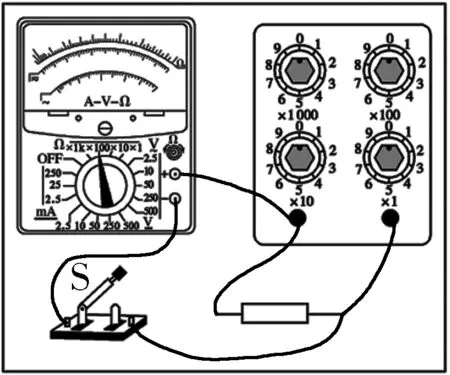
圖4
10.(1)將鋼球置于軌道平直段各處,都能保持靜止,說明斜槽末端水平 (2)球心(3
11.(1)設物塊2 到達傳送帶A端時的速度為vA,根據動能定理得m(gsinθ-,解得vA=。設兩物塊碰后黏合體的速度為,根據動量守恒定律得mvA=2mvA',解得。(2)設黏合體沿光滑半圓形軌道CDE上升的最大高度為h,根據動能定理得2mvA'2,解得h=0.5 m,即黏合體從C點沿光滑半圓形軌道CDE運動到與圓心等高的D點速度減小為0,再從D點返回至停止運動。根據動能定理得2mgh-2μmgs路=0,解得s路=1 m,即黏合體最后停在傳送帶B端。(3)設黏合體到達E點時的速度為vE,根據平拋運動規律得,解得。黏合體從B點運動到E點,根據動能定理得-2μmg·2d-2mg·2R=,解得。因為vB<vA',所以黏合體在傳送帶上做減速運動。若黏合體從A點一直做減速運動到B點,根據動能定理得,解得。因為vB>v,所以黏合體在傳送帶上先做減速運動后做勻速運動,傳送帶的轉動速度v傳=。
12.(1)設導體棒1剛進入磁場區域時的速度為v,根據動能定理得,解得。此時回路中的感應電動勢最大,且E=BLv,回路中的感應電流I=,導體棒2 受到的安培力F=BI·2L,導體棒2的最大加速度滿足F=2ma,解得。(2)導體棒1 進入磁場后做減速運動,導體棒2做加速運動,當v1=2v2時,回路中的感應電動勢為0,感應電流為0,兩導體棒分別達到穩定的勻速運動狀態,導體棒1 在水平軌道上運動的過程中有,導體棒2 在水平軌道上運動的過程中有,解得。(3)兩導體棒剛好達到穩定狀態時,整個回路中產生的熱量,導體棒1中產生的熱量,解得。
13.(1)ADE (2)(ⅰ)設玻璃管的橫截面積為S,則右側管內封閉空氣柱的初狀態體積V右1=5S,環境溫度升高的過程中右側管內封閉空氣柱的壓強不變,根據蓋-呂薩克定律得,解得右側管內封閉空氣柱的長度L=5.83 cm。(ⅱ)大氣壓強p0=75 cmHg,右側管內封閉空氣柱的初狀態壓強,左側管內封閉空氣柱的初狀態壓強90 cmHg,左側管內封閉空氣柱的初狀態體積V左1=32S。環境溫度升高后,設左側管內水銀面下降的高度為h,左側管內封閉空氣柱的末狀態壓強,左側管內封閉空氣柱的末狀態體積V左2=(32+h)S。對左側管內封閉空氣柱應用理想氣體狀態方程得,解得h=3 cm。
14.(1)ACE (2)(ⅰ)光束a經折射后恰好射到AD邊的中點,如圖5所示,根據幾何關系得,根據折射率公式得n=,解得。(ⅱ)設光束a在AD邊上剛好發生全反射,則光束a在P點的折射角β滿足解得。根據數學知識得,根據折射率公式得,解得。當光束a經折射后剛好射到D點時,有sinβ,根據,解得。因此光束a在AD邊上發生全反射,sinθ的取值范圍為。
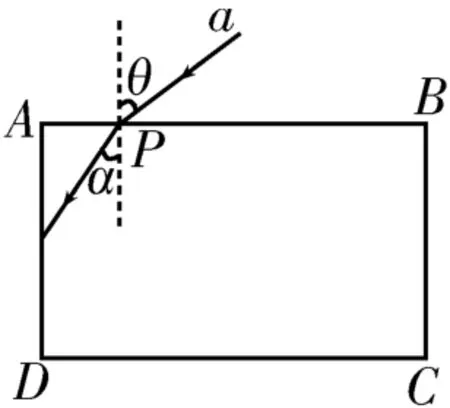
圖5

