基于Vague集的航空電子對抗裝備維修等級劃分研究

高 嵩，胡俊萌，王 欣

(1.空軍工程大學航空機務士官學校，河南 信陽 464000；2.解放軍95580部隊，貴州 貴陽 550000)

0 引 言

隨著航空電子對抗裝備技術水平不斷發展，裝備數量不斷擴充，裝備的結構復雜程度進一步加深，裝備維修的要求也變得更高。但是目前航空電子對抗裝備的維修體制已不能完全滿足裝備需求，存在裝備故障等級和維修等級劃分不清、復雜設備維修程序不清等問題，從而造成維修任務分工劃分不合理，裝備維修時間長、維修困難等問題。

通過建立航空電子對抗裝備維修等級分析模型，開發配套的維修信息管理系統，可以快速對裝備的故障等級和維修等級進行定位，確定維修主體和維修程序，縮短裝備維修時間，對提高裝備管理的科學性、裝備完好率具有重要意義。

1 基于Vague集的多目標決策理論

Gau和Buehrer于1993年提出了一個新的處理模糊信息的模糊理論——Vague集。與Fuzzy集一樣，在Vague集中給每個對象分配一個隸屬度，但不同的是這個隸屬度是[0，1]之間的一個子區間，這個區間既包含了支持x∈X的證據，同時又有反對x∈X的證據。同Fuzzy集相比，Vague集能更準確地表達出對象的模糊信息，本文基于Vague集對航空電子對抗裝備的維修等級進行劃分。

定義1[1]：令X是一個點(對象)的空間，其中的任意一個元素用x表示，X中的任意一個Vague集用一個真隸屬函數tV和一個假隸屬函數fV表示，tV是從支持x∈X的證據所導出的隸屬度下界，fV是從否定x∈X的證據所導出的隸屬度下界，tV(x)和fV(x)將區間[0，1]的一個實數與其中的每一個點聯系起來，即：tV:X→[0,1],fV:X→[0,1]。其中，tV+fV≤1。此時稱V(x)=[tV(x),1-fV(x)]為X上的Vague值，稱V=[tV,1-fV]為X上的Vague集。

定義2[2]：稱Vague集G={〈x,GT(x),GF(x)|x∈U〉}為i-vVague集，其中U是論域，i-v模糊集合GT(x)，GF(x)分別表示x∈U關于G的真隸屬度函數和假隸屬度函數：

GT(x)=[aT(x),bT(x)]?[0,1]

(1)

GF(x)=[aF(x),bF(x)]?[0,1]

(2)

且有bT(x)+bF(x)≤1。

定義3[3]：i-vVague集G為H所包含(G?H)定義為：GT(x)?HT(x)且HF(x)?GF(x)。

以上是關于Vague集的3個基本定義，也是運用Vague集分析問題的基礎。

2 基于Vague集的裝備維修等級分析模型

根據以上定義，在航空電子對抗裝備維修等級劃分中，修理級別有2種可以選擇，分別為基層級和基地級。假設其構成的集合記為A,本文確定了影響維修等級劃分標準的8種因素，因此評價這2種維修級別好壞的標準有8種，分別是故障模式、維修費用、維修難度、維修條件、維修時間、故障頻度、備件數量及采購價格。假設其構成的集合為B，根據Vague集的基本理論，對于任意待評價的維修級別Ai∈A在評價標準Bj∈B下的隸屬函數可以用i-vVague集表示為如下形式：

uij=〈GTij,GFij〉

(3)

式中：GTij=[aTij,bTij]表示維修級別Ai在評價標準Bj下的滿意程度區間；GFij=[aFij,bFij]表示維修級別Ai在評價標準Bj下的否定程度區間，并同時滿足i-vVague集的如下條件：bTij+bFij≤1,1≤i≤m,1≤j≤n。

按照以上方法可以得出m×n的矩陣R：

(4)

式中：μij=〈[aTij,bTij],[aFij,bFij]〉,1≤i≤m,1≤j≤n。

簡記為：R={〈[aTij,bTij],[aFij,bFij]〉}mn。 矩陣R稱為維修級別的集合A和評價標準的集合B之間的關聯矩陣，關聯矩陣反映了維修級別的集合A和評價標準的集合B兩者之間的數學關系，以下的論述都是基于關聯矩陣R的基礎之上。

根據權重分析系統[4]，假設評價標準集合B中的各個評價標準的權重為ω，即：ω=(ω1,ω2,…,ωn)T。令：λ=(λ1,λ2,…,λm)T=R·ω，所以λi可以作為維修級別Ai的綜合評價，在這里稱為評價函數E，即：

(5)

此時的評價函數是Ai關于評價標準集B的i-vVague集，也包含2個部分，其中GTi表示維修級別Ai在評價標準集B下的滿意程度區間；GFi表示維修級別Ai在評價標準集B下的否定程度區間。在這里可以看出雖然得出了評價函數E，但由于它是2個區間值，并不能直觀地看出維修級別的好壞，還必須尋求一種算法能給出一個具體的值，也就是一個函數，在這里稱為決策函數[5]：

(6)

(7)

即S(E(Ai))≤S(E(Ai+1))。說明滿意程度越大、否定程度越小的維修級別評價函數值越高，則選取評價函數值高的維修級別符合決策者的要求，可以采用這個評價函數對決策目標進行選擇。

3 指標權重的確定

在以上維修等級劃分模型中，權重的確定是輸出結果可靠的關鍵，一般在多目標決策中，決策問題大都有各方面決策人員共同參加。因此，加權法是求解多目標決策問題最常用最主要的方法。這就需要一個描述指標相對重要程度權重的估計。指標的權重應該是指標在決策中相對重要程度的一種主觀評價和客觀反映的綜合度量。本文根據集值統計和模糊區間分析，并考慮到專家權重中的權威質量、熟悉度、謹慎度等指標確定了權重分析系統。

通過對影響維修等級劃分標準的因素進行分析可知，這些指標需要專家對決策指標進行半定性、半定量的分析、評價，這種評價包含很多不確定性的、模糊的、隨機的成分。不同的評價者對同一評價指標的評價結果不會相同；而即使同一個評價者，對同一評價指標在不同的時間、環境及所得信息量的影響，其評價結果也可以不相同。因此，在評價過程中，往往只給出指標評價值的一個區間。為了處理這種問題，集值統計提供了一個合適的工具。

假設有m個指標，記為x1,x2,…,xm，由n個專家對每個指標進行評價，要求每個專家對各個指標根據線段法給出各指標權重的區間估計值，假設評價結果如表1所示[6]。

表1 n個專家對m個指標的評價結果

考慮任一指標xi的各專家評價值，這是一個集值統計序列[ain,bin]，每個區間的前項是指標i權重的最小可能值，后項是指標i權重的最大可能值。這n個區間疊加在一起形成覆蓋在評價值軸上的一種分布，如圖1所示。對于指標xi，把區間[aimin,bimax]分為y等份，那么每等份的長度為Y：

圖1 n個評價區間疊加示意圖

Y=(bimax-aimin)/y

(8)

對任一小區間[aimin+(j-1)Y,aimin+jY]，可以定義各專家在該區間內的特征函數：

(9)

假設n個專家的權重分別為W1,W2,…,Wn，則區間j的置信度可以定義為：

(10)

由此方法可以得到指標xi評價值y個區間的置信度u(1),u(2),…,u(y)，如圖2所示。

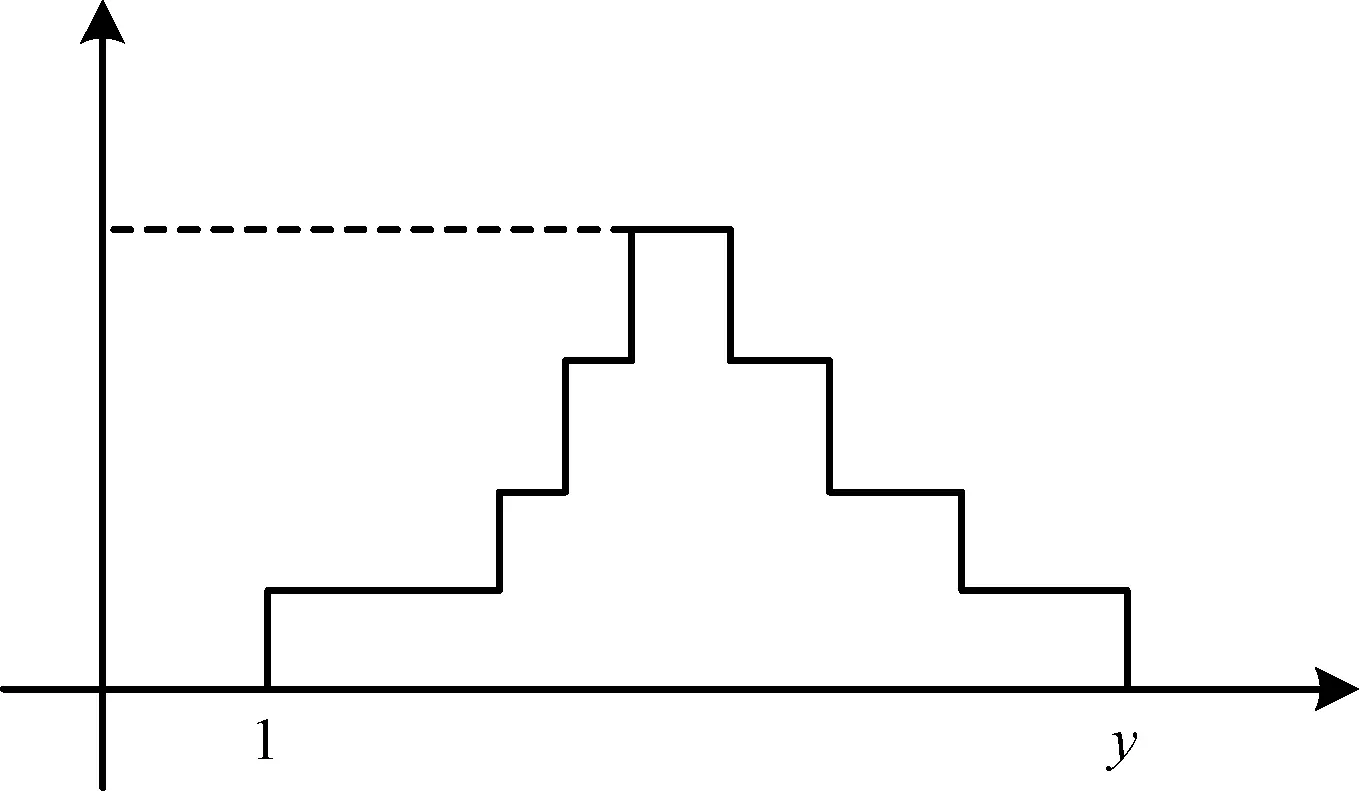
圖2 y個區間置信度示意圖

對于置信度序列,可以取λ截集(λ閾值可以由專家確定)，那么可以得到一個連續序列u(pi),u(pi+1),…,u(qi)。其中pi≥1，qi≥y，pi，qi為正整數，顯然這是置信度序列的一部分，是區間[aimin,bimax]中qi-pi+1個連續的小區間，把這些小區間合并在一起可以得到：[aimin+piY,aimin+qiY]。這樣，就得到了根據專家評價意見、考慮各專家權重經統計得到的指標xi的權重區間值，就可以得到m個指標權重范圍。對于權重范圍可以有3種準則：一是樂觀準則，把區間投影到最大值；二是悲觀準則，把區間投影到最小值；三是平均準則，把區間投影到平均值。采用平均原則，那么可以得到指標xi的權重為：

ei=[aimin+piY+aimin+qiY]/2=

aimin+(pi+qi)Y/2

(11)

歸一化后，可以得到任意指標xi的權重為：

(12)

4 應用實例

根據上文分析，維修級別有2個，為基層級和基地級；評價維修級別的經濟性因素有8個，分別為故障模式、維修費用、維修難度、維修條件、維修時間、故障頻度、備件數量、采購價格等。邀請3位專家進行評價，其權重分別為0.4、0.3、0.4，假設有5個內場可更換單元(SRU)需要進行維修等級劃分評價，分為權重的確定和維修等級計算2個部分。

4.1 權重的確定

假設1、2、3號專家對8個指標給出的評價區間值分別如表2所示。

表2 3個專家對8個指標的評價區間值

在統計計算過程中，對各指標取閾值均為λ=1，經統計可以得到8個指標的權重區間ωi，采用平均值方法可以得到各指標權重ei，經歸一化后可得到各指標的權重e′i，所得結果如表3所示。

表3 3個專家對8個指標的權重評價結果

4.2 維修等級計算

假設2種可供選擇的維修級別分別記為A1，A2，按照影響維修等級劃分總結出的8個因素分別記為B1,B2,…,B8，決策者對每個裝備(模塊)修理等級的劃分要從這2種維修級別里選擇一種作為最佳維修方式，選擇的標準依據影響維修等級劃分的因素和相應的權重得出決策函數。其中任一維修級別Ai(1≤i≤2)在評價標準Bj(1≤j≤8)下的隸屬函數用i-vVague集表示，如表4所示。

表4 維修級別Ai在約束條件Bj下的i-vVague集

根據3位專家對8個約束條件的權重計算，可得評價函數和相應的決策函數如表5所示。

表5 維修級別Ai的評價函數和決策函數

從表5的計算結果可以看出，S(E(A1))>S(E(A2))，這說明維修級別A1(基層級)更適合于當前待評價的裝備(模塊)，從以上的實例也可以看出，通過建立維修級別和評價標準之間的i-vVague集，通過專家打分、結果計算等過程，就能夠對當前待評價的裝備(模塊)選擇合適的維修等級。

5 結束語

航空電子對抗裝備維修保障是確保裝備完好率、提高裝備作戰效能的重要工作。建立航空電子對抗裝備維修等級分析模型，能夠對裝備的故障等級和維修等級進行準確定位，規范裝備的維修程序。實踐表明本文中的方法和系統軟件具有顯著的實用價值。在下一步工作中，可在維修級別評估指標的選取和專家打分的權重確定方面進行優化。