面向多目標資源受限的航空維修保障工序調度方法研究

魏夢媛，渠懷賡，孫 坤

（中國飛行試驗研究院，陜西 西安）

引言

資源受限工序調度問題(Resource-constrained Project Scheduling Problem,RCPSP)是指在滿足項目時序要求和多種資源的約束下，確定所有任務的開始時間及結束時間，使得總時間最短[1]。合理地調節各項目活動的開始時間和資源使得能夠有效地縮短項目完工時間，在實際航空維修保障過程中具有非常重要的意義。目前這類問題的研究主要集中在工期單目標優化問題上[2]。實際航空維修保障中，單一指標難以評價方案優劣，需考慮多個指標并進行權衡，本文將維修保障人力資源的合理配置作為工序調度問題的目標，考慮維修人員數量的情況下，兼顧維修工序的緊前約束條件，基于RCPSP 構建維修保障時間和資源配置的多目標優化函數，采用快速非支配排序遺傳算法(NSGA-II)對案例進行求解分析，實現在合理安排人力資源對工序進行維修的同時，維修時間最短，即合理利用維修資源，盡快完成維修任務。

1 修保障資源均衡多目標優化數學模型

資源受限情況下，實現航空維修保障過程時間最短、資源合理配置，可以歸結為多目標優化問題。

此類問題的數學描述如下

針對實際航空維修保障過程，主要從維修工序、維修時間、維修人力資源3 個方面構建優化模型：優化目標為時間最短、人力資源合理配置；約束條件為資源數量和維修工序緊前約束條件。

1.1 目標函數

1.1.1 維修時間最短目標

假設一個維修項目中包括N 個工序，其中活動1和活動N 為虛擬活動，分別作為項目的開始和項目的結束。

T 為總時間，則目標函數為

以人力資源需要量的標準偏差作為均衡配置評價函數，數學模型表達如下

將Q 作為評價資源配置均衡的目標函數，當Q 越小，維修人員分配的擁擠程度越低，人員調配使用越合理，目標函數為

1.2 約束條件

維修保障過程中存在2 種約束關系：一是維修人員的數量約束，即對工序中任意時刻，正在進行的工序的維修人員總數，不超過限制的數量；二是緊前約束關系，即兩個工序具有必然的先后關系[3]。如工序1和工序2 具有緊前約束關系，則工序2 的開始時間晚于工序1 的結束時間。

在整個維修項目中有如下假設：

a.單個工序的活動具有連續性，不存在停頓；

b.各工序緊前關系保持不變；

c.各種資源之間相互獨立，不存在相關關系。

維修保障資源分配數學模型構建可以描述如下：一是維修人員須按照維修手冊內容逐步完成所有工序，在前一項工作還沒有完成的情況下，不能進行下一步活動；二是維修人員總數有限，每步工序所需維修人員數量是一定的，同一時刻進行的所有工序所需要的維修人員的數量之和應不大于總的維修人員數量；三是維修人員只有在進行完上一步維修活動后，才可以繼續下一項，不能同時進行兩項維修活動；四是總的維修時間的約束，完成最后一項維修保障活動的時刻T 不能大于總的維修保障時間，T 即為實際總維修保障時間。數學模型可以描述為

式（6）表示所有的最早、最晚開工時間應滿足工序排布邏輯條件，且資源利用在受限范圍內。

2 基于NSGA-II 的多目標優化算法

以上優化模型為多目標規劃問題，一般不可能存在一個使每個目標都達到最優的解，本文選擇快速非支配排序遺傳算法-NSGA-II 作為多目標優化算法，可以得到一組均衡解，稱為最優非劣解集或Pareto最優解集[4]。

NSGA-II 算法的基本思想如下。

第一步隨機生成大小為N 的初始種群，對該種群進行非支配排序，再根據遺傳算法，進行選擇、交叉、變異操作，可以得到第一代子代種群；從第二代子代種群開始，合并父代種群與子代種群，進行快速非支配排序，計算擁擠度，包括非支配層的所有個體，根據個體之間的關系和擁擠度，選擇出有優勢的個體，形成新的父代種群；再重復第二步，通過遺傳算法中的選擇、交叉、變異操作形成新的子代種群，直到達到設定的循環數，或達到符合結合的條件[5]。

NSGA-II 算法主要的優化策略包含以下3 個方面。一是快速非支配排序，這一步根據個體的優勢排列將種群中個體排序；二是擁擠度比較算子，根據個體擁擠程度選擇進入下一代進行循環迭代的個體，保持種群多樣性；三是精英保留策略，對應第二步，合并父代和子代個體再優先選擇優秀個體，作為下一代種群，這一步能夠保留歷代計算出的最優個體。NSGA-II算法流程見圖1。

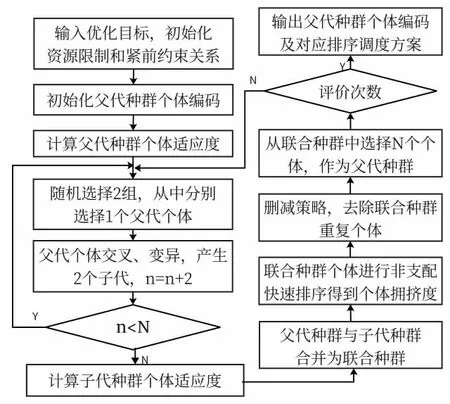
圖1 NSGA-II 算法流程框圖

3 基于isight 平臺構建的多目標優化流程

以吊艙軟管更換試驗為例進行分析。機務維護人員總數量為8 人。在吊艙拆卸試驗工序中，B、C、F，G四個工序屬于可并行工作。根據據緊前工序排列原則，得到各工序的最早開工時間和最晚開工時間，并按實際工作中統計的各工序持續時間與人員數量，給出表1 中的試驗流程邏輯關系。

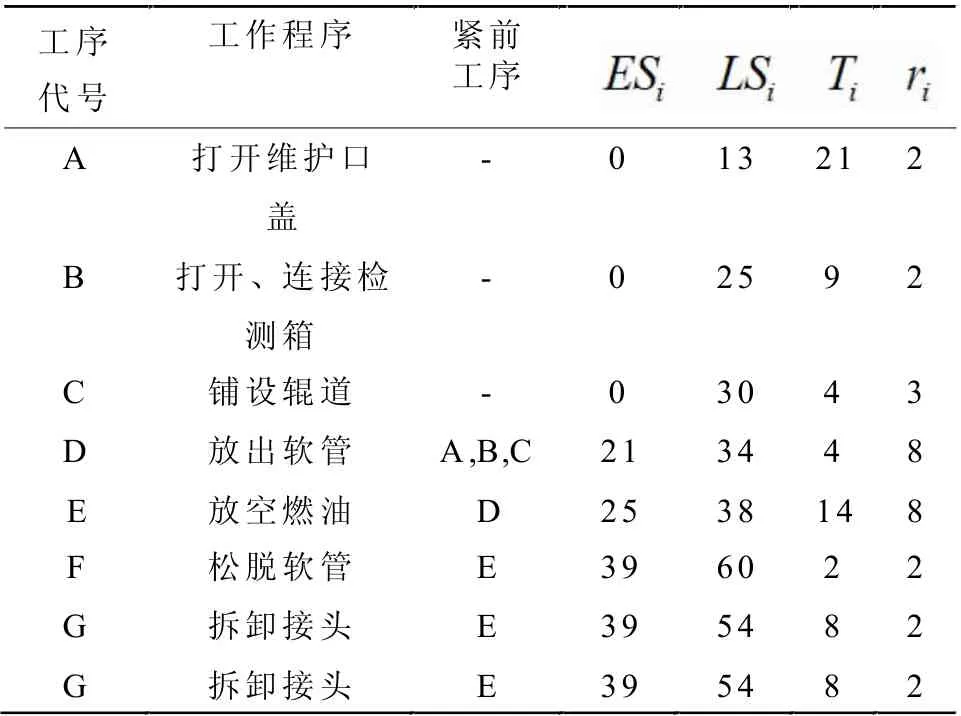
表1 專項試驗流程邏輯關系及時間表

在Matlab 軟件中，對前文中給出的優化目標和約束條件指標進行編程求解。

對多目標函數的優化設計，采用Isight 封裝的NSGA-II 方法。以Isight 軟件為平臺，集成Matlab 軟件完成并聯機構的多目標優化。如圖2 所示，搭建并聯機構多目標優化流程圖，箭頭為數據和過程傳遞路徑。

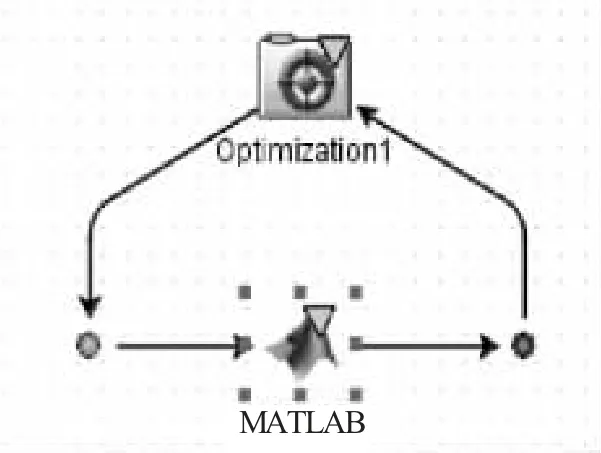
圖2 ISIGHT 調用Matlab

通過多目標優化最終得到可行的設計點，對結果的選擇提供重要的參考。圖3 中可以看出可行點和不可取的劣解的分布。各設計點數值見表2。表2 的6 組結果中，后3 組結果均為較優，其中第6 組的資源均衡評價指標Q 與總時間T 都為最小，對應最優情況。

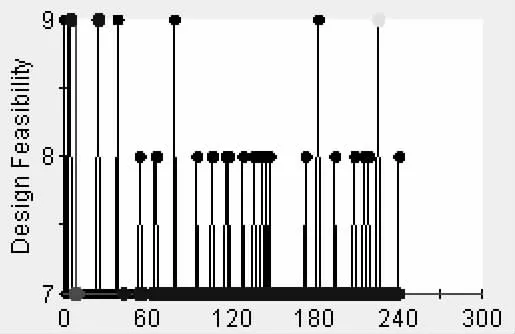
圖3 可行解與最優解

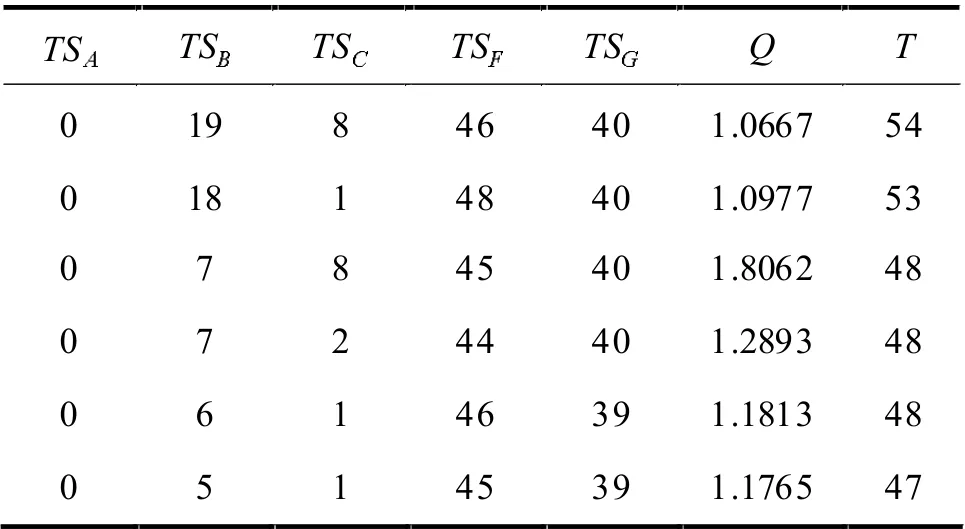
表2 優化結果及相應工序排列情況

優化前和優化后共7 組結果見圖4。

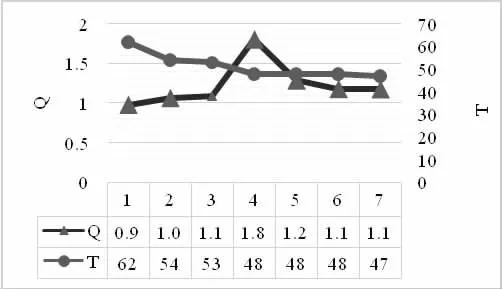
圖4 優化結果對比

圖4 中第一組數值為優化前的目標值，可以看出，通過多目標優化，對工序進行調度排布，使得維修保障時間逐漸縮短，其中最優組時長為47 min，人員標準偏差也相應達到了低區間，這說明整個過程對于人力資源的配置實現了均衡優化。

4 結論

本研究針對航空維修保障過程中資源受限情況，構建了資源約束與維修保障時間最短、人力資源均衡配置多目標數學優化模型，結合NSGA-II 多目標優化算法，在Isight 平臺中實現維修保障資源均衡多目標優化流程，可以達到時間縮短、資源均衡配置的目標。本研究提出的方法可以為航空維修保障工序調度提供參考。