輪胎有效滾動半徑與負荷半徑特性研究

張保軍 李論 呂滿意 王偉 馮勇

（中國第一汽車股份有限公司研發總院，長春 130013）

1 前言

輪胎有效滾動半徑（簡稱滾動半徑）和負荷半徑是輪胎的2個重要基本參數，在輪胎模型研究、輪胎性能試驗、整車性能仿真、車輛設計和車輛控制系統開發中有著廣泛應用。部分間接式胎壓監測系統基于滾動半徑進行監測，其原理是輪胎的氣壓變化影響輪胎滾動半徑的大小，進而影響輪速，通過分析輪速信號即可反映滾動半徑的變化，完成對輪胎氣壓的監測[1]。

目前對滾動半徑和負荷半徑的研究一般只考慮載荷、速度、氣壓的影響，側偏角和外傾角的影響考慮較少。MF-Tyre 模型中給出了滾動半徑的經驗公式[2]，但試驗量要求較大[3]。

為完善對滾動半徑和負荷半徑變化規律的認識，減少試驗工作量，本文從試驗和回歸模型2個方面對滾動半徑和負荷半徑進行研究，采用均勻試驗設計方法設計試驗方案，借助偏最小二乘回歸方法建立回歸模型。

2 偏最小二乘回歸

當自變量間存在嚴重多重相關性時，普通最小二乘法失效，采用此方法計算時會破壞參數估計，擴大模型誤差，并使模型喪失穩健性。為解決此問題，有學者提出了偏最小二乘回歸方法。偏最小二乘回歸能夠在自變量存在嚴重多重相關性的情況下進行回歸建模，并允許在樣本點數量少于自變量數量的情況下進行回歸建模[4]。

MATLAB 軟件提供了偏最小二乘回歸函數Plsregress，偏最小二乘回歸的應用步驟為：

a.對數據進行標準化處理。

b. 使用MATLAB 函數Plsregress 進行偏最小二乘回歸。

c.對回歸模型的參數進行檢驗，檢驗方法可采用Bootstrap 法[4]。如有未通過檢驗的自變量，將其刪除，重復步驟b。

d. 將關于標準化變量的回歸模型轉化為關于原始變量的回歸模型。

3 滾動半徑和負荷半徑特性

影響輪胎半徑的因素很多，如輪胎的載荷、氣壓、速度、外傾角、側偏角、路面曲率、所用輪輞規格等。本文暫不考慮后2 種因素的影響，在MTS Flat-Trac CT Ⅲ高速平帶試驗臺上進行試驗，使用的輪胎規格為205/55 R16。

3.1 載荷、氣壓、速度的影響

通常，研究人員最關心輪胎的載荷、氣壓、速度對半徑的影響，此時不考慮側向力和縱向力的影響。

為減少試驗次數，部分因子設計是常用的方法，其中正交試驗設計和均勻試驗設計應用最為廣泛。

對于大部分試驗，特別是探索性試驗，試驗人員對試驗的統計模型往往所知甚少，需要通過試驗獲得近似模型，需采用均勻試驗設計（簡稱均勻設計）方法進行試驗設計。

正交設計假定模型的形式已知，需要通過試驗來估計模型中的未知參數，且試驗的次數（強烈依賴于未知參數的數量）隨因素數量的增加呈指數增長[5]。

根據實際情況采用均勻設計表U25(53)[5]，試驗設計情況如表1、表2所示。

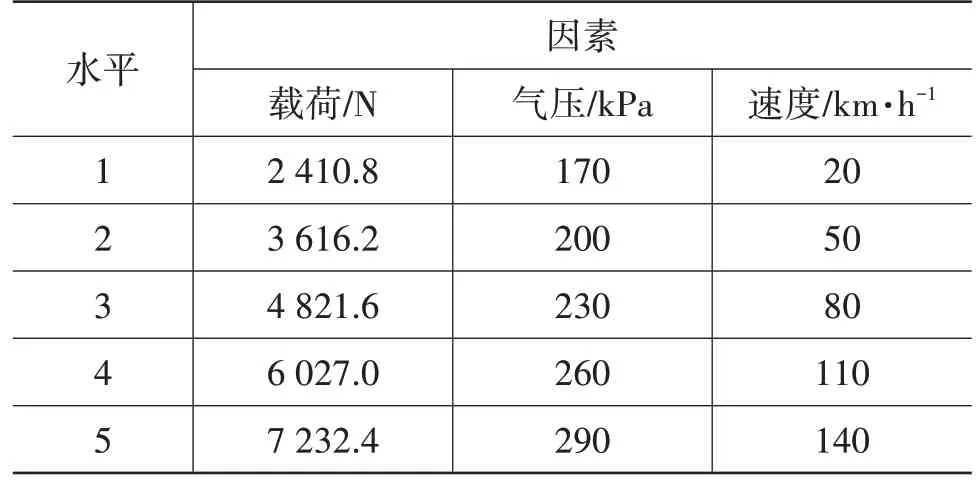
表1 三因素水平表

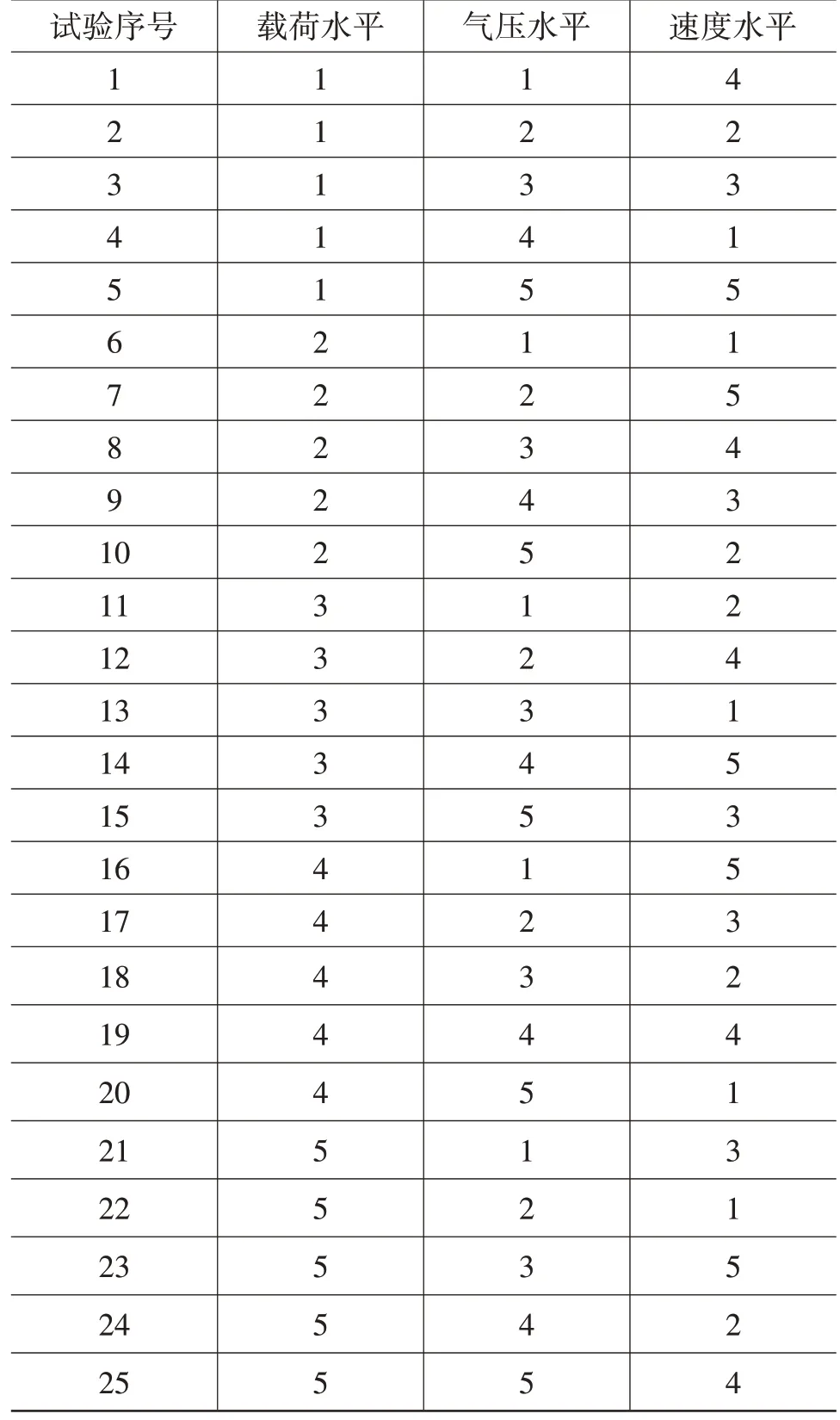
表2 均勻設計表U25(53)

輪胎充氣壓力采用調壓方式，試驗過程中充氣壓力保持不變。

滾動半徑測量采用輪胎移動距離與旋轉角度計算獲得，負荷半徑為輪軸中心到接地印跡中心的距離。

利用偏最小二乘回歸法，得到滾動半徑的回歸模型為：

同樣可得負荷半徑回歸模型為：

式中，re、rl分別為滾動半徑和負荷半徑；v為速度；p為氣壓；Fz為載荷。

圖1 所示為三因素回歸模型的殘差統計結果。由圖1可知，滾動半徑和負荷半徑的殘差均很小，最大絕對值分別為0.21 mm 和0.52 mm，誤差平方和分別為0.30 mm2和1.72 mm2，所得回歸模型的精度較高。

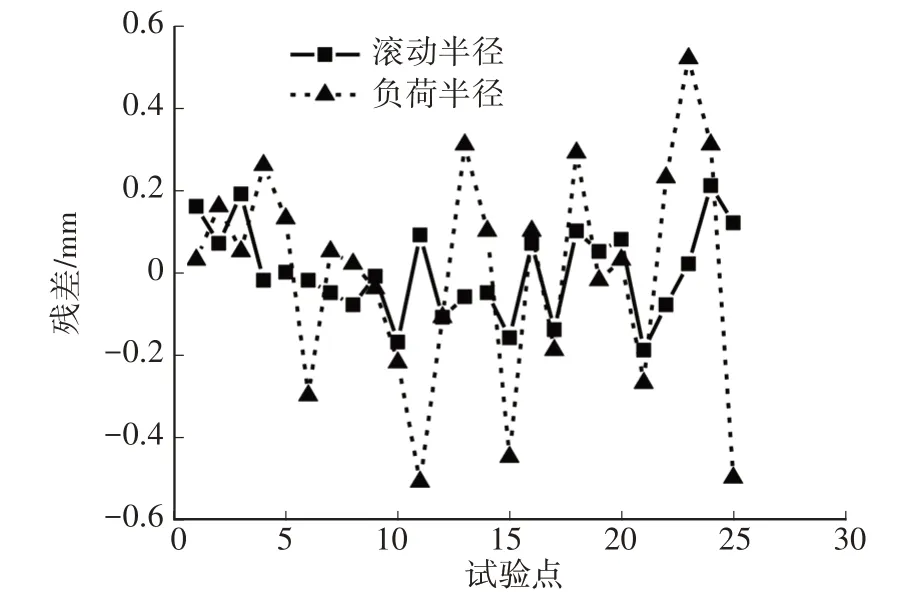
圖1 三因素回歸模型殘差

在MF-Tyre 6.2模型中，沒有顯式的負荷半徑公式，提供了如下滾動半徑公式[2]：

式中，Cz0為名義載荷和名義氣壓下的垂直剛度；Fz0為名義載荷；R0為自由半徑；RΩ為離心力作用下的自由半徑；Cz為垂直剛度；dpi為氣壓無量綱增量；qFz1、qFz2分別為載荷與變形的一階系數、二階系數；pFz1為垂直剛度的氣壓影響系數；Dreff為滾動半徑的峰值系數；Breff、Freff分別為滾動半徑的低剛度系數、高剛度系數。

根據試驗數據對MF-Tyre 模型進行參數辨識，得到參數為pFz1=0.85、qFz1=10.57、qFz2=9.82、Dreff=0.23、Breff=4.67、Freff=0.026。圖2所示為MF-Tyre 模型的滾動半徑殘差結果。由圖2 可知，殘差最大絕對值為1.05 mm，誤差平方和為5.98 mm2，所得模型的精度較回歸模型的精度低。

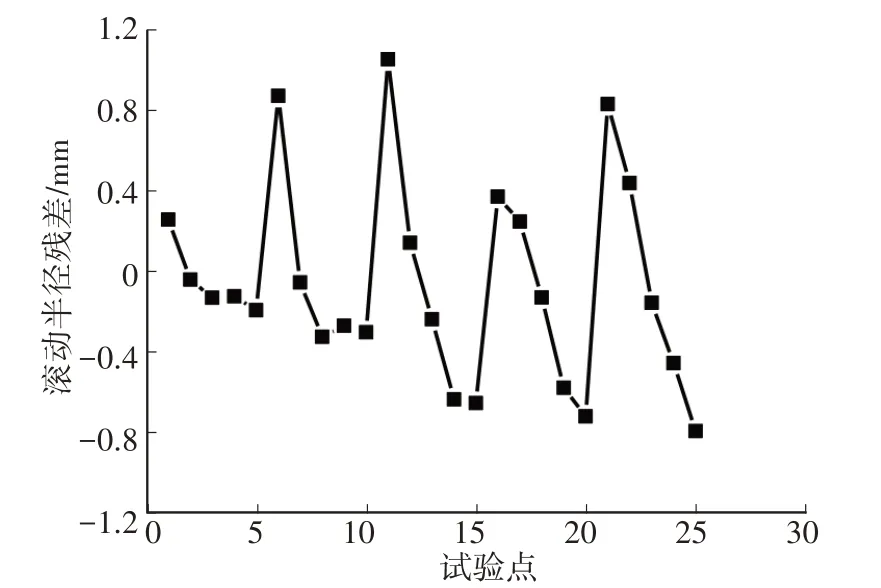
圖2 MF-Tyre模型殘差

為分析載荷、氣壓、速度對半徑的影響，采用上述回歸模型進行模擬，結果如圖3所示。

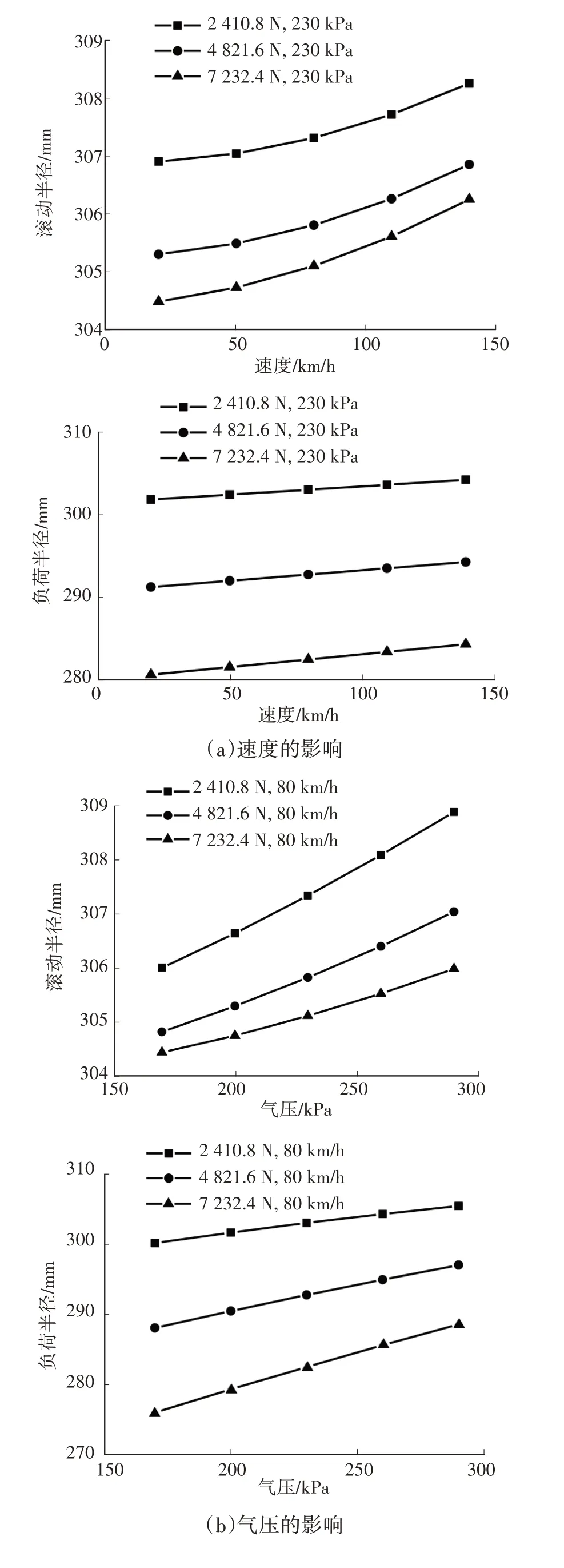
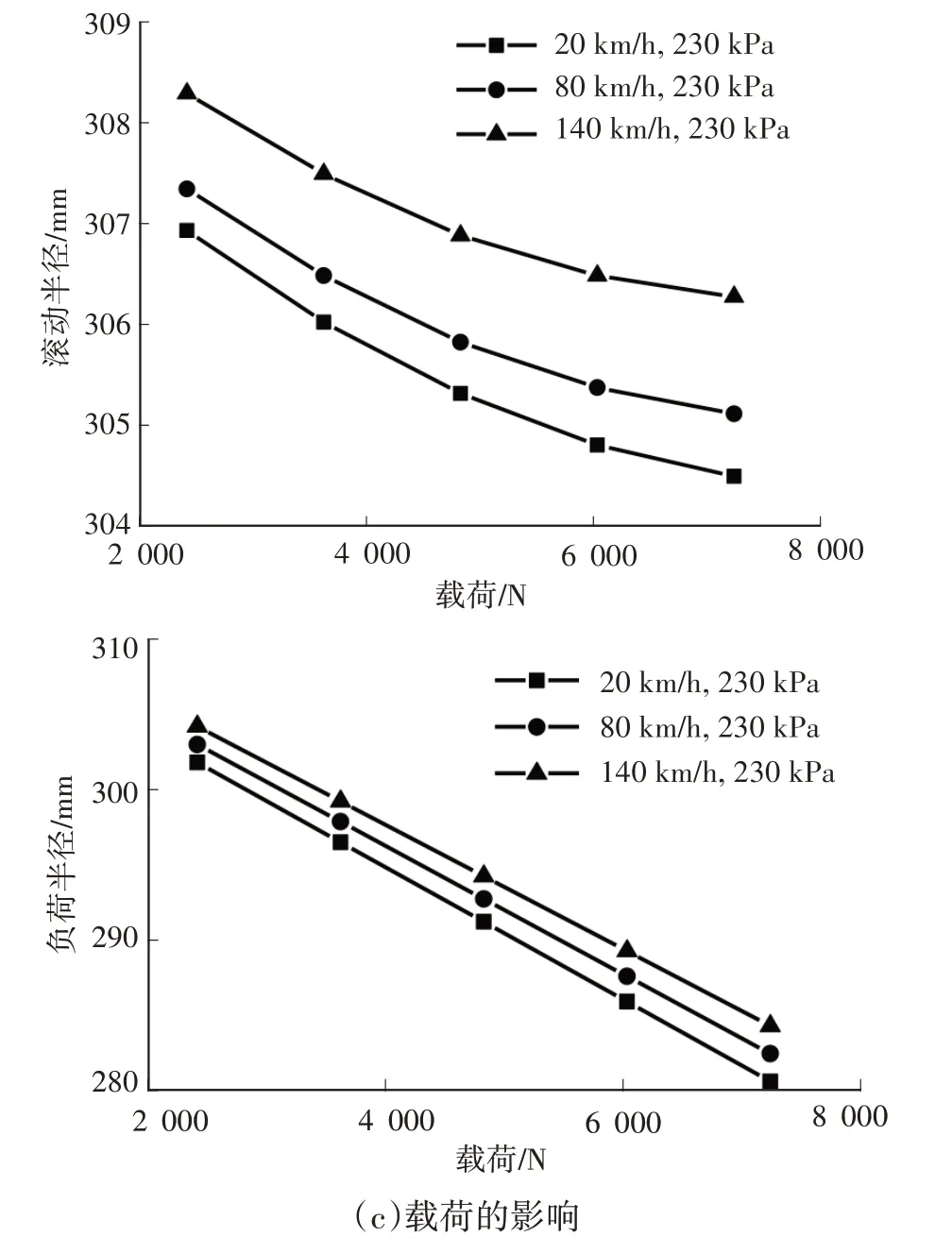
圖3 回歸模型模擬曲線

由模擬結果可知：滾動半徑、負荷半徑隨速度提高而增大，隨氣壓提高而增大，隨載荷增加而減小；滾動半徑對速度、氣壓、載荷不敏感，負荷半徑對速度、氣壓不敏感，對載荷敏感。如：在速度為80 km/h、載荷為4821.6 N 的條件下，氣壓從170 kPa 增加到290 kPa，滾動半徑僅增加2.23 mm，負荷半徑卻增加了8.95 mm；在速度為80 km/h、氣壓為230 kPa 的條件下，載荷從2410.8 N 增加到7232.4 N，滾動半徑僅減小2.23 mm，負荷半徑卻減小20.54 mm。

由式（2）和圖3 可知，負荷半徑與速度、載荷成線性，與氣壓近似成線性。

3.2 外傾角的影響

為分析外傾角對滾動半徑和負荷半徑的影響，進行試驗研究。試驗載荷分別為2410.8 N、4821.6 N、7232.4 N；氣壓為230 kPa；速度為80 km/h；側偏角為0°；外傾角分別為-10°、-6°、-4°、-2°、-1°、0°、1°、2°、4°、6°、10°。試驗結果如圖4所示。

由圖4 可知：外傾角的存在使得滾動半徑減小、負荷半徑增大；隨著外傾角絕對值的增加，滾動半徑逐漸減小、負荷半徑逐漸增大，正、負外傾角的影響基本相等；隨著載荷的增加，外傾角對滾動半徑和負荷半徑的影響變小。本文所得結果與文獻[6]所述趨勢基本一致，但該文獻只給出了單一載荷條件下負荷半徑曲線，未給出滾動半徑曲線。

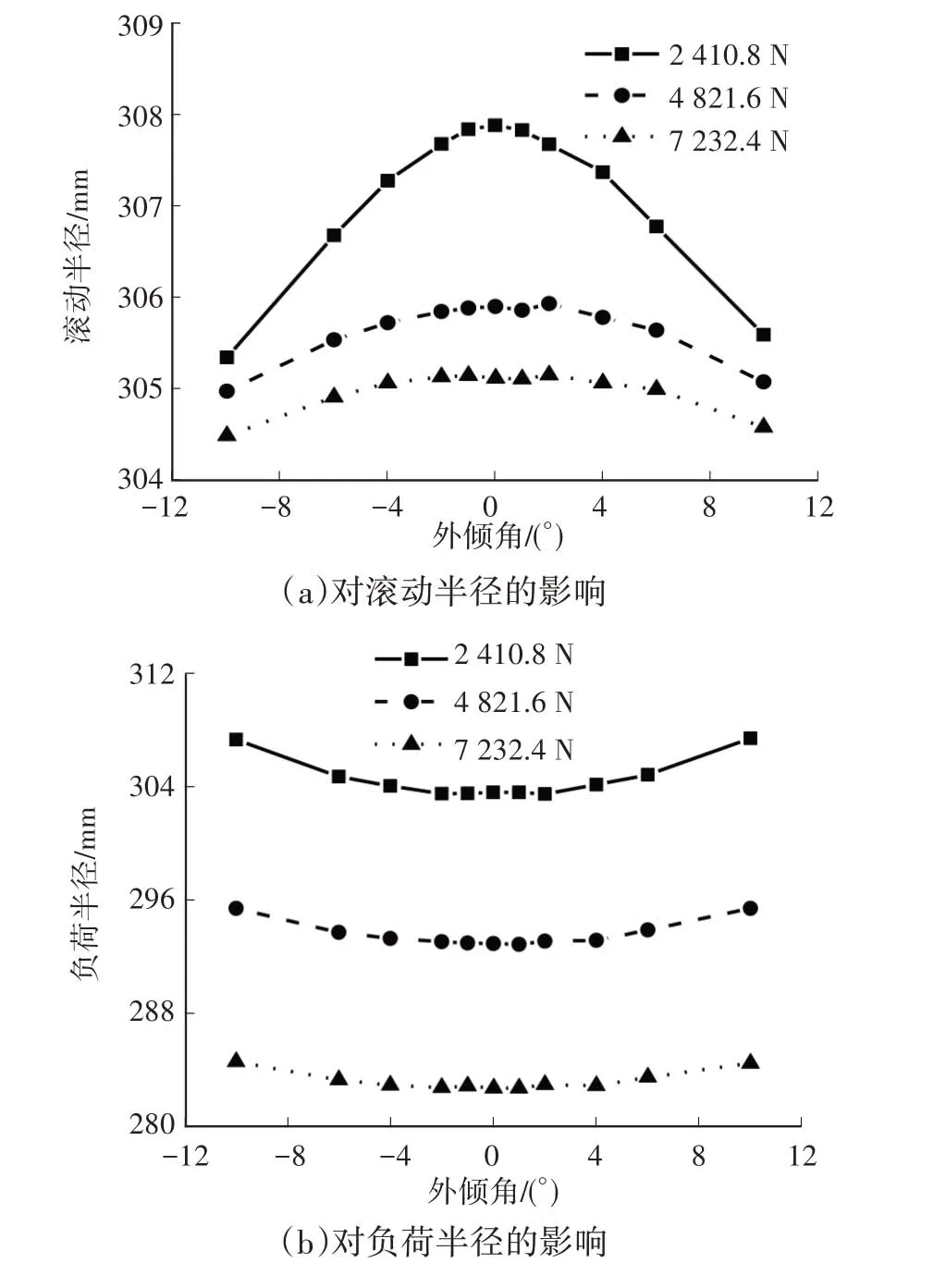
圖4 外傾角對滾動半徑和負荷半徑的影響

3.3 側偏角的影響

為分析側偏角對滾動半徑和負荷半徑的影響，進行試驗研究。試驗載荷分別為2410.8 N、4821.6 N、7232.4 N；氣壓為230 kPa；速度為80 km/h；側偏角分別為-10°、-6°、-2°、0°、2°、6°、10°；外傾角為0°。試驗結果如圖5所示。

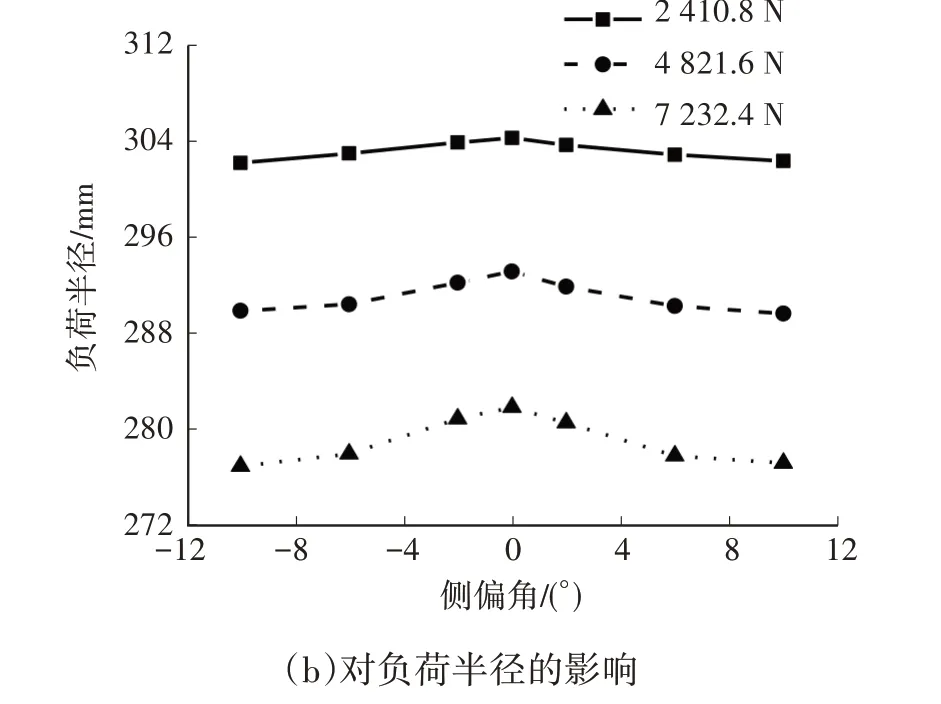
圖5 側偏角對滾動半徑和負荷半徑的影響

由圖5 可知：側偏角的存在使得滾動半徑增大、負荷半徑減小；隨著側偏角絕對值的增加，滾動半徑增大、負荷半徑減小，正、負側偏角的影響基本相等；隨著載荷的增加，側偏角對負荷半徑的影響變大。所得結果與文獻[6]所述趨勢基本一致，但該文獻只給出了滾動半徑曲線，未給出負荷半徑曲線。

為觀察胎面磨損對半徑的影響大小，進行如下試驗：試驗1，測試0°側偏角下的滾動半徑和負荷半徑；試驗2，進行不同載荷、側偏角不為0°的試驗；試驗3，重復試驗1。由試驗1、試驗3 測得半徑的減少量，如表3所示。

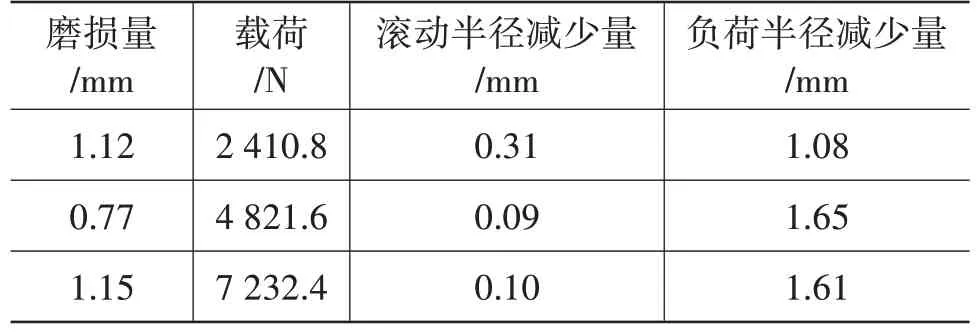
表3 磨損對半徑影響

由表3可知：隨著胎面磨損的增加，滾動半徑和負荷半徑均減小，磨損對滾動半徑影響小，滾動半徑的減小量小于磨損量；磨損對負荷半徑影響更大；磨損量不等于半徑的減少量。為減少干擾因素，提高試驗精度，在進行側偏角不為0°的試驗時，要盡量減小輪胎磨損。

3.4 四因素綜合影響

四因素包括載荷、氣壓、速度、外傾角，試驗中側偏角為0°。為全面分析四因素的影響，選用均勻設計表U25(54)[5]進行試驗設計，試驗設計情況如表4、表5所示。

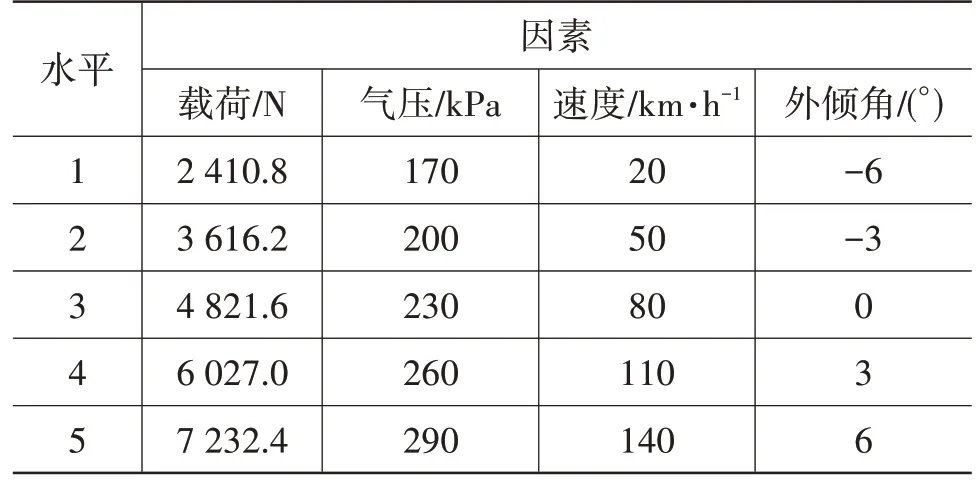
表4 四因素水平表

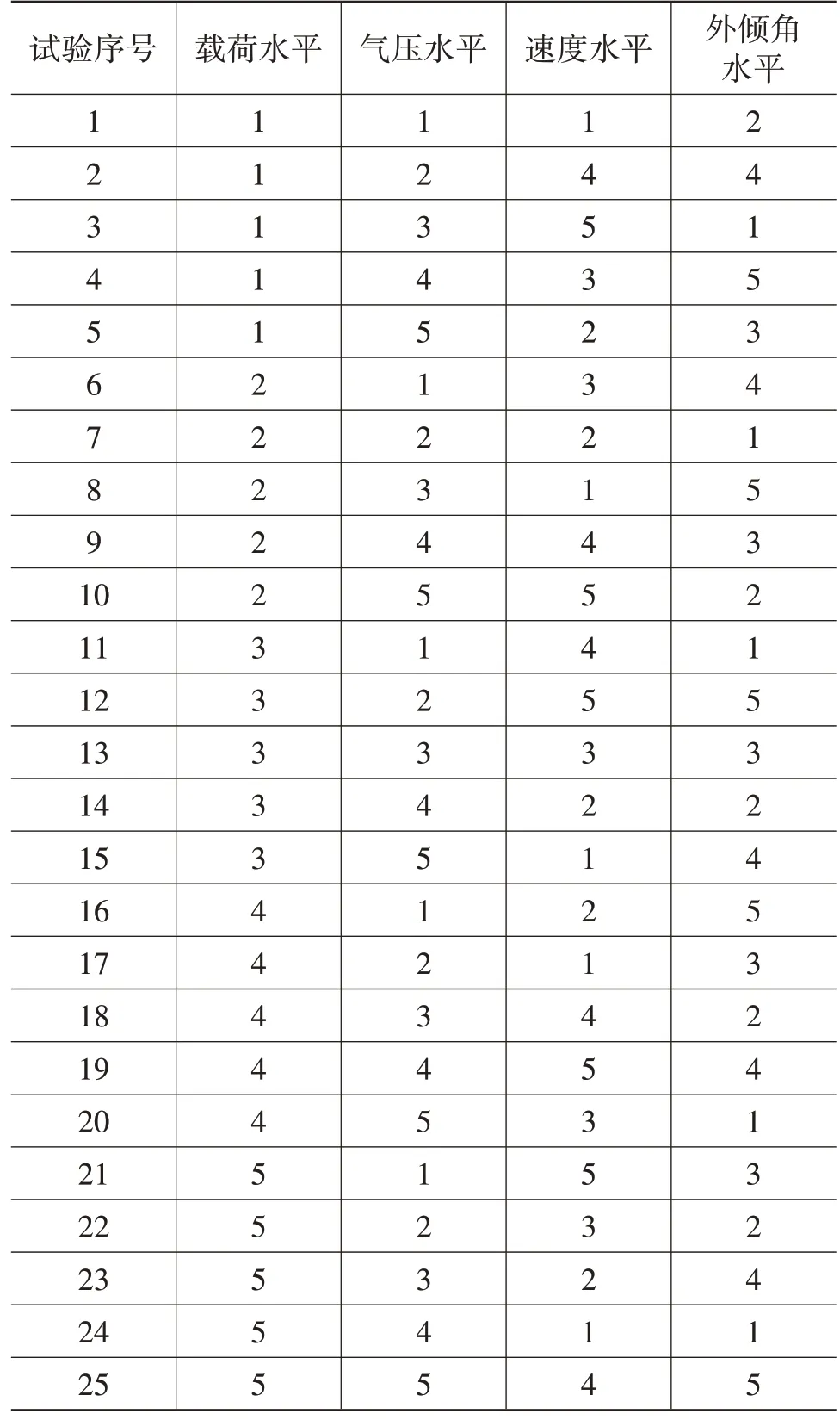
表5 均勻設計表U25(54)

利用偏最小二乘回歸法，得到關于滾動半徑的回歸模型為：

同樣可得負荷半徑回歸模型為：

式中，γ為外傾角。

圖6 所示為四因素回歸模型的殘差。由圖6 可知，滾動半徑和負荷半徑的殘差均較小，最大絕對值分別為0.47 mm 和0.44 mm，誤差平方和分別為0.62 mm2和0.90 mm2，所得回歸模型的精度較高。

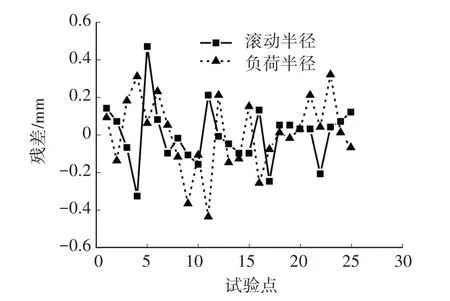
圖6 四因素回歸模型殘差

為驗證回歸模型的預測能力，利用式（6）、（7），對3.2 節中的試驗進行仿真，并與試驗結果進行對比，如圖7 所示。由圖7c 可知：二者差別較小，除了2 個點外，殘差絕對值均小于0.5 mm；滾動半徑和負荷半徑殘差的最大絕對值分別為0.94 mm和1.25 mm（均發生在載荷為2410.8N、外傾角為±10°處）。此處殘差大的原因包括：外傾角超出試驗范圍，計算屬于外推；小載荷時滾動半徑變化劇烈，是建模的難點。所得回歸模型在小載荷條件下預測誤差稍大，總體預測能力較強。

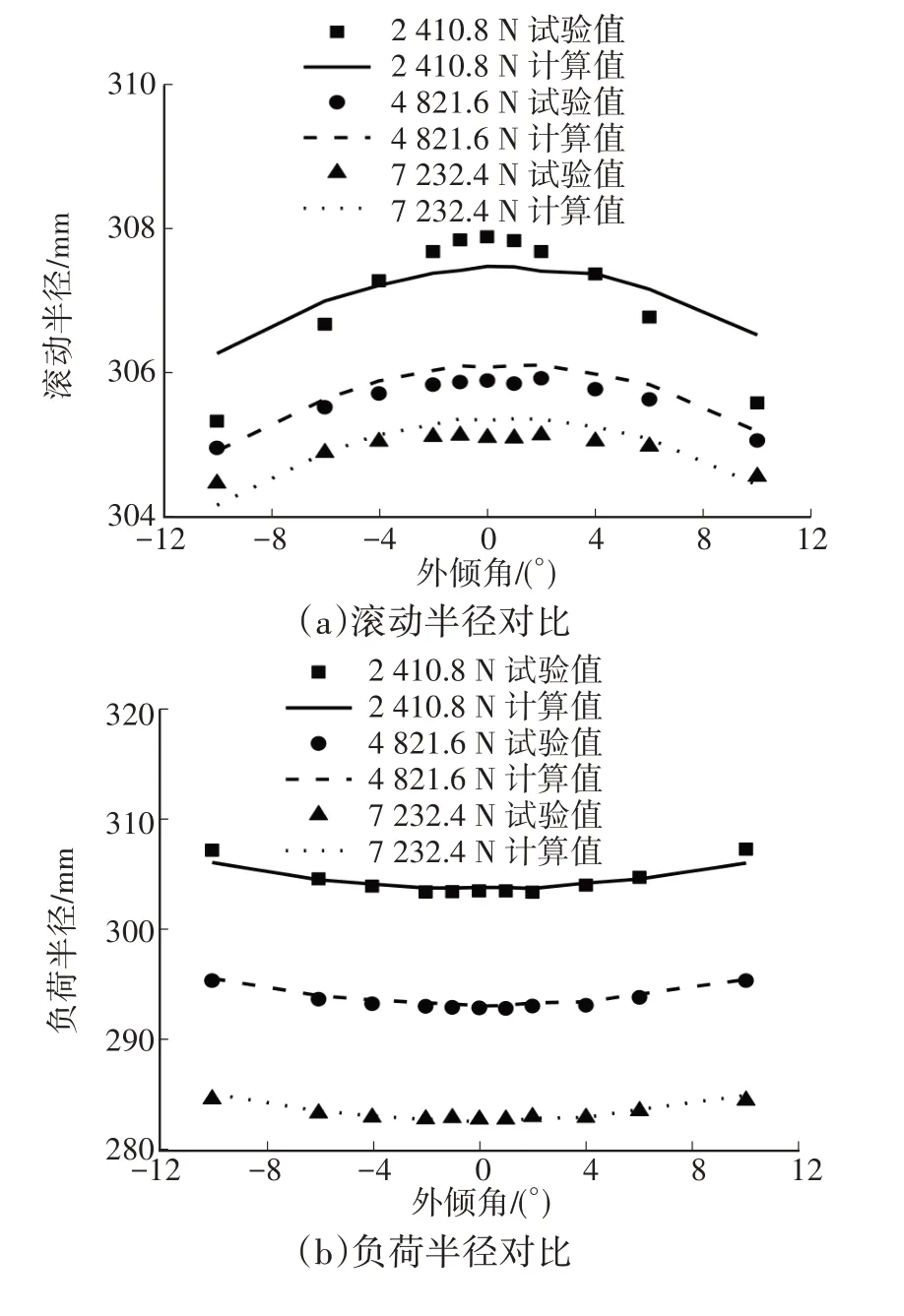
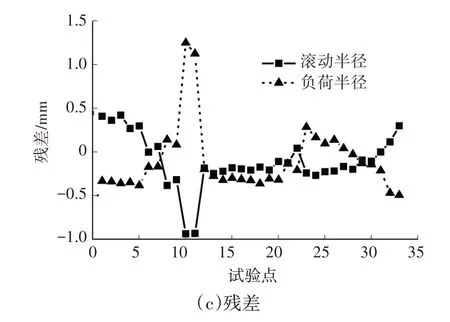
圖7 外傾角對滾動半徑和負荷半徑影響的試驗與仿真對比

4 結束語

通過以上研究，得出以下結論：

a.本文采用均勻設計方法設計了試驗方案，減少了試驗次數；采用偏最小二乘回歸方法得到的回歸模型精度較高，在不考慮側向力和縱向力影響的工況下，精度要高于MF-Tyre 模型，預測能力較強，較好地描述了各因素與滾動半徑（負荷半徑）的關系。

b.滾動半徑、負荷半徑受速度、氣壓、載荷影響的趨勢基本一致，影響程度不同，負荷半徑與速度、載荷成線性相關。

c.外傾角和側偏角對滾動半徑、負荷半徑的影響不同。外傾角的存在使得滾動半徑減小、負荷半徑增大；側偏角的存在使得滾動半徑增大、負荷半徑減小。

d.隨著胎面磨損的增加，滾動半徑和負荷半徑均減小，磨損對滾動半徑影響小，對負荷半徑影響更大；磨損量不等于半徑的減少量。